●华腾飞 (黄湾中学 安徽灵璧 234213)

分类讨论是一种重要的数学思想方法，也是一种重要的解题策略.可是由于分类讨论过程一般较为冗长，叙述繁琐，并且还容易出现错误.因而在历年的各地高考试题中，它不仅经常出现在基础性很强的选择题、填空题中，而且更多的是渗透在综合性的解答题中，是高考中难度比较大的一类考题.下面结合实例谈谈避免和优化分类讨论的几种技巧，这不仅可以使解题过程大为简化，而且还可以提高解题速度和解答的正确率.

1 巧用性质

例1 设定义在［-4，4］上的偶函数f(x)在区间［0，4］上单调递增，若 f(2-a)＜f(a)，求实数 a的取值范围.

分析由f(x)的定义域为［-4，4］，得a，2-a∈［-4，4］.但 2-a，a 在［-4，0］，［0，4］的哪一个区间内需要进行讨论.如果巧用“若f(x)是偶函数，则f(-x)=f(x)=f(|x|)”这一性质，那么可避免大规模的讨论，从而简化求解过程.

解由f(x)是偶函数，得

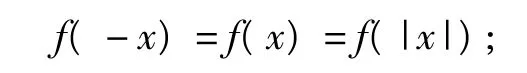
由 f(a-2)＜f(a)，得

又当 x∈［0，4］时，f(x)递增，因此

例2 已知方程x2+x+k=0的2个根为α，β，且|α -β|=3，求实数 k.

分析实系数一元二次方程的2个根可能均为实根，也可能为一对共轭虚根，无论哪种情形，总有|α -β|2=|(α -β)2|.利用这一性质可以避开讨论，从而使运算过程大大简化.

解据题意，由一元二次方程根与系数的关系知

由已知|α -β|=3，得

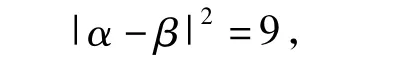
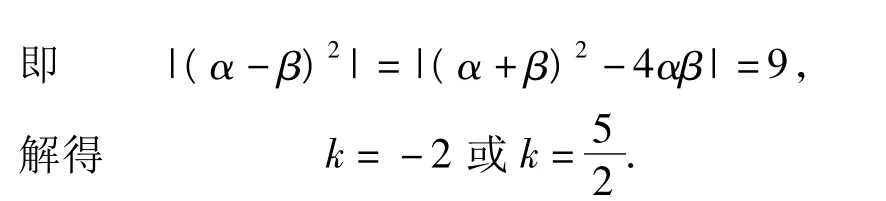
分析若分a＞0，a＜0，再结合对称轴与给定的区间3种位置关系，则要分6种情形进行讨论，非常繁琐.如果注意到“二次函数在闭区间上的最值只能在区间的端点或抛物线顶点处取得”，那么可以使讨论过程大大优化.

2 活用法则

例4 设{an}是由正数组成的等比数列，Sn是其前n项和，求证：

若用a1及公比q表示Sn，则必须分q=1和q≠1进行讨论.若紧紧抓住等比数列前n项和的隐含定义Sn+1=a1+qSn，则可避免讨论，优化解题过程.

简证 因为

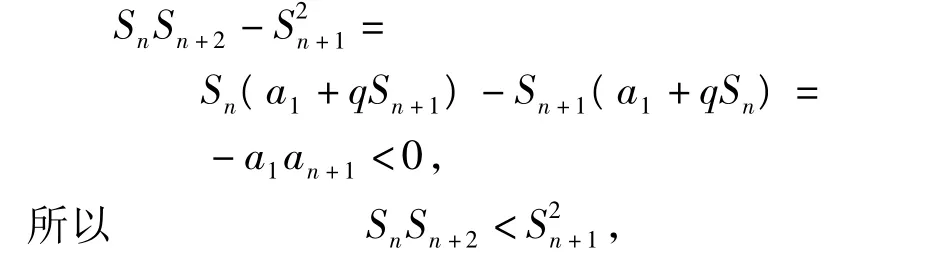
故原命题得证.

例5 设 0＜x＜1，a＞0且 a≠1，试比较|loga(1-x)|与|loga(1+x)|的大小.

分析比较大小的常用方法是作差比较或作商比较.本题若直接采用作差比较，则需要考虑底数a＞1，0＜a＜1这2种情况进行，很繁琐;若用作商比较再结合换底公式，则可避开讨论.下面的解法则更令人拍手叫绝.

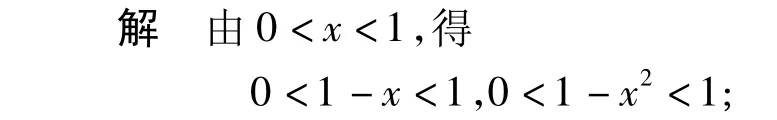
又由 a＞0，a≠1，得 loga(1-x)与 loga(1-x2)同号.因为

3 整体换元

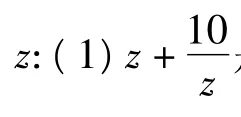
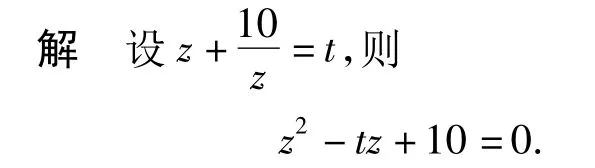
据条件(1)知，t为实数，且1 ＜t≤6，则

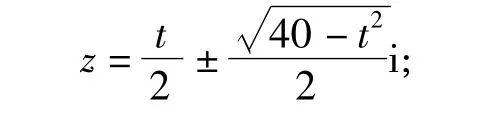
综上所述，z=1 ±3i，或 z=3 ±i.

4 整体变形

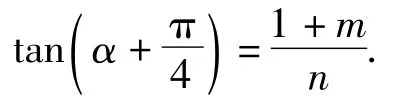
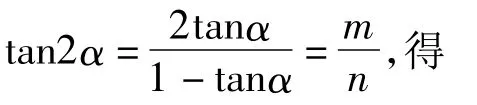
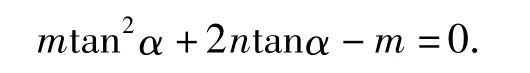
这不仅要对m=0和m≠0进行分类讨论，而且还要求出tanα的2个值，十分复杂.若将待证式进行整体变形，则大大简化解题过程.

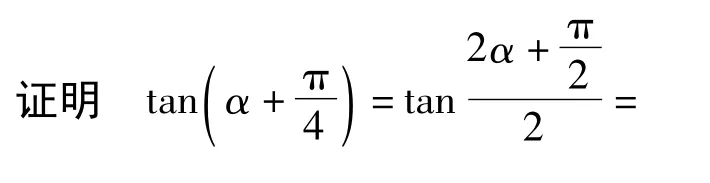
5 巧设方程

例8 直线l过抛物线y2=2px(p＞0)的焦点，并且与抛物线相交于点 A(x1，y1)，B(x2，y2)，求证：4x1x2=p2.

分析若直接设直线l的点斜式方程，则必须单独讨论直线l与x轴垂直的情况.若巧设直线l的方程为x=my+n，则可避免讨论，直达彼岸.

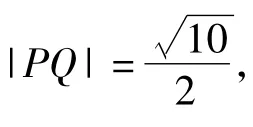
分析由题设条件不能确定焦点在哪条轴上，因此可避免讨论，设椭圆方程为Ax2+By2=1(A＞0，B ＞0).

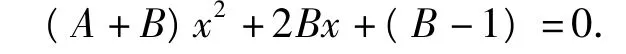
设点 P，Q 的坐标分别为 P(x1，x1+1)，Q(x2，x2+1)，则

将式(1)，式(2)代入式(3)，得

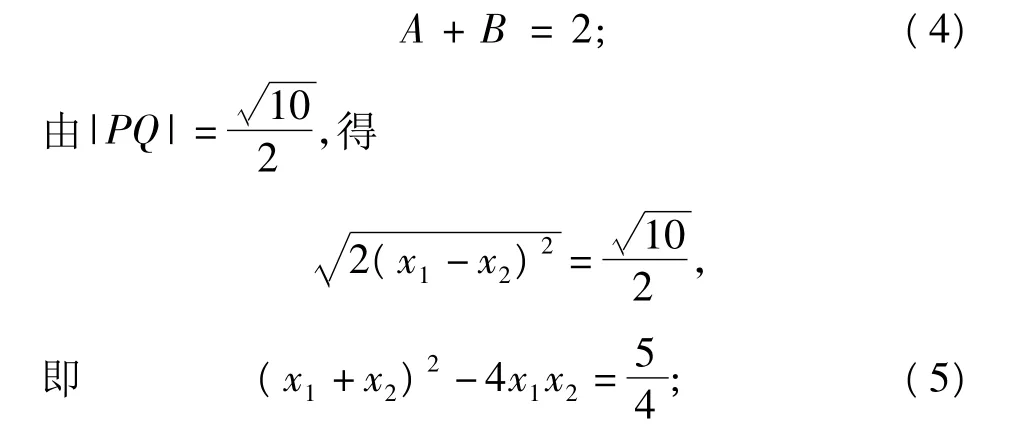
将式(1)，式(2)代入式(5)，得

5A2+5B2+26AB-16A-16B=0. (6)将式(4)代入式(6)，解得

评注椭圆方程Ax2+By2=1同时表示了焦点在x轴、y轴上的2种形式，用待定系数法求方程时较为简便.另外，当双曲线的焦点所在的轴不易确定时，其标准方程也可用Ax2+By2=1来表示.若设直线方程，则不应设为y=k(x+x0)，而应设为ky=x+x0，因为这样可以避免讨论k存在和不存在这2种情况.

例10 求中心在原点，对称轴是坐标轴，一条渐近线是3x+2y=0，且经过点P(8，6)的双曲线方程.

分析由于题设未明确给出焦点的位置，若设2个双曲线方程(实轴在x轴或y轴上)，利用待定系数求解过繁;若先由点P及渐近线的位置确定焦点位置，则可简化解题过程，但不如直接利用共轭双曲线系方程求解更优.

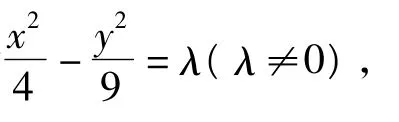
故所求的椭圆方程为

6 分离参数

例11 已知不等式cos2θ+2msinθ-2m-2＜0对任意实数θ恒成立，求实数m的取值范围.

则由|sinθ|≤1知，应对m分3种情况进行讨论，相当繁琐.若采用分离参数的方法，把已知不等式等价转化，则可简单、快速地获解.

解原不等式等价于

7 消去参数

例12 设 0＜x＜1，a＞0且 a≠1，试比较|loga(1-x)|与|loga(1+x)|的大小.

分析若按常规方法考虑去绝对值符号，则应分a＞1与0＜a＜1这2种情况进行讨论，很繁琐;若注意到2个对数同底，用作商比较法，则可用换底公式消去参数a，避开讨论.

8 数形结合

例13 设 a，b是2个实数，A={(x，y)|x=n，y=na+b，n 是整数}，B={(x，y)|x=m，y=3m2+15，m 是整数}，C={(x，y)|x2+y2≤144}，是直角平面xOy内的点集合，是否存在 a和 b使得：(1)A∩B≠φ;(2)(a，b)∈C 同时成立?

分析由条件(1)可取na+b=3n2+15，即

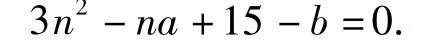
把该式看成关于未知数a，b的二元一次方程，它在直角坐标平面aOb内表示一条直线，于是由

构成的关系式组是否有实数解，取决于直线xa+b-(3x2+15)=0与圆x2+y2=144的位置关系.

解如图1所示，动点(a，b)在直线l上，直线l：nx+y-(3x2+15)=0与圆 x2+y2=144应有公共点，但原点到直线l的距离

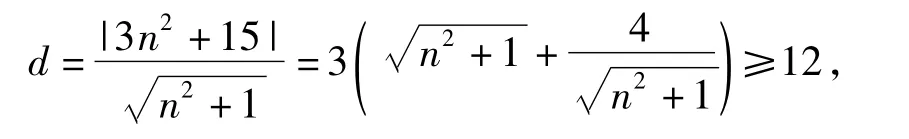
且因为n是整数，上式等号不成立.故同时满足条件(1)，(2)的 a，b不存在.

图1

9 正难则反

例14 已知f(x)=(m-2)x2-4mx+2m-6的图像与x轴有2个交点，其中至少有一个在x轴的负半轴上，求实数m的取值范围.

分析根据题意，直接用分类讨论求解，有3种可能的情形，而原问题的反面只有1种情形“2个交点都不在x轴的负半轴上”，若抓住反面求解，则会非常简捷.

解设2个交点 A(x1，0)，B(x2，0)都不在 x轴的负半轴上，则

10 反客为主

例15 设k为实数，试求出关于x的方程x4-2kx2+k2+2k-3=0的实根范围.

解把原方程整理为k的二次方程k2+2(1-x2)k+(x4-3)=0且k为实数，得

评注若把x看作主元，令x2=t进行换元，再对k进行分类讨论，则很难获解.

11 补集分析

例16 如果二次函数y=mx2+(m-3)x+1的图像与x轴的交点至少有一个在原点的右侧，求m的取值范围.

解先考虑二次函数图像与x轴的2个交点都在原点的左侧的情况，即一元二次方程mx2+(m-3)x+1=0有2个负根，可得

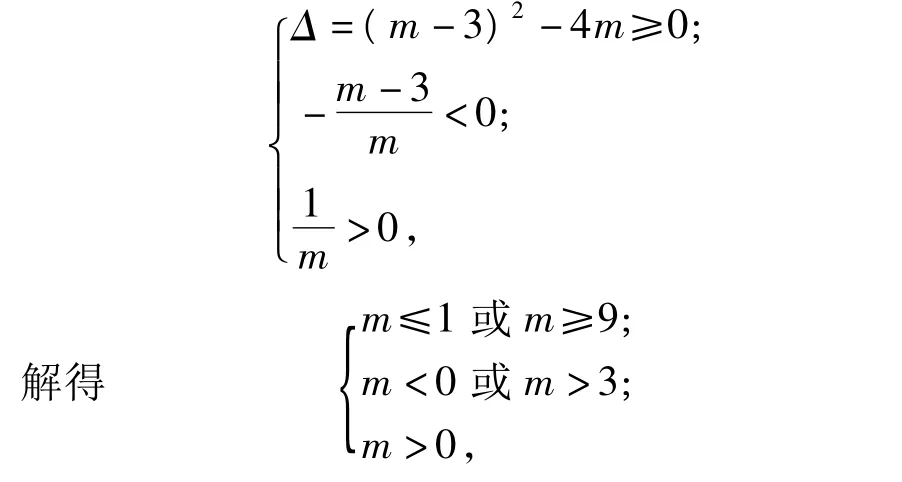
故当m≥9时，2个交点在原点的左侧.

上述解集的补集为m＜9，但Δ≥0与m≠0是必须同时满足的条件，故二次函数的图像与x轴的交点至少有一个在原点右侧的条件为：m≤1且m≠0.

评注上述方法是从反面进行思考，而前提条件是Δ≥0及m≠0，在采用这种方法时极易被忽视，希望能够引起大家足够的重视.

12 巧用对称

故f(x)为偶函数.

当 x＞0时，2x＞1，即1-2x＜0，故有f(x) ＜0;据偶函数的性质知，当x＜0时，亦有f(x)＜0;故当 x≠0时，恒有 f(x)＜0，即

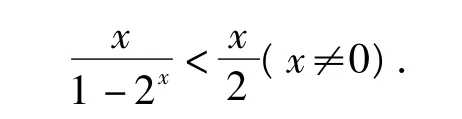
评注利用偶函数的对称性和奇函数的中心对称性，常能使所求解的问题避免复杂的讨论.

总之，对于一个具体的问题，是否需要讨论，以什么作为标准去讨论，要根据题目所给条件及要求去确定.若能采用等价转换、整体构造、换元等有效措施，结合定义、性质和直观图形，优化和避免分类讨论，则将会使人们的思维进入一个崭新的境界.