樊玉环 ， 马艳芬，蒋超凡

（黑龙江工程学院数学系，黑龙江哈尔滨 150001）

关于保持问题的研究，许多学者做了大量的工作，取得了丰富的成果，文献［1］研究了全矩阵空间上的保幂等的函数的形式，文献［2］研究了域上上三角矩阵空间的保持幂等的函数，但关于保对合的函数的文章至今还没有，文献［3］及文献［4］从不同矩阵空间上研究了保幂等的加法映射，文献［5］研究了保逆的线性算子，文献［6］从交换整环上研究保持问题，有关这一领域的研究资料可参看文献［7］-文献［14］。文献［15］给出了幂等矩阵与对合矩阵的关系，然而利用文献［1］及文献［2］所给出的幂等矩阵，再利用文献［15］所得到的对合矩阵，却得不到函数的形式，本文重新选取特殊的对合矩阵，得到域上全矩阵空间及上三角矩阵空间的保持对合的函数的形式。

1 符号及基本概念

设F是特征不为2的域，F＊表示F＼｛0｝，M n（F）为F上所有n阶矩阵的全体，T n（F）为F上所有n阶上三角矩阵的全体，A f=f（aij）。

定义1［15］称A是对合矩阵，如果A满足A2=In。

定义2［14］称函数f：F→F是域上全矩阵空间的保持对合的函数，如果f满足

称函数f：F→F是域上上三角矩阵空间的保持对合的函数，如果f满足

定义3［15］称f：F→F是同态，如果f满足f（a＋b）=f（a）＋f（b），f（ab）=f（a）f（b）。

2 全矩阵空间上保持对合的函数

定理1 函数f是M n（F）（n≥4）上保持对合的充要条件是f=±δ，其中δ是域F上的自同构。

证明 充分性显然，下面证明必要性。

步骤一：证明f（0）=0，f（1）=±1。

由=I n，得（）2=I n。通过计算得：

由式（2）得f（0）=0或2f（1）=（2-n）f（0）。若将f（0）=0代入式（1）得f2（1）=1。若将2f（1）=（2-n）f（0）代入式（1）得f2（0）=故分为4种情况。

情况一：f（0）=0，f（1）=1；

情况二：f（0）=0，f（1）=-1；

情况三：f（0）=

情况四：f（0）=

以下证明情况三不成立，利用类似的方法可证情况四也不成立。

通过计算得：

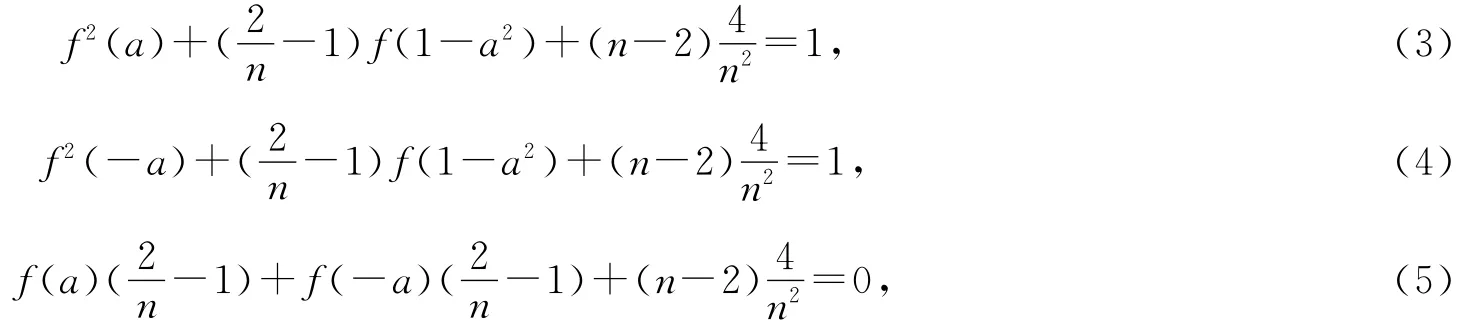
由式（5）得f（a）＋f（-a）=，再由（3）-（4）得f2（-a）=f2（a），故f（a）=，∀a∈F，与f（1）=-1矛盾。故情况三不成立。

以下步骤二到步骤五证明情况一。即已知f（0）=0，f（1）=1。

步骤二：证明f（-a）=-f（a）。

通过计算得：

步骤三：证明f（xy）=f（x）f（y）。

通过计算得：

在式（7）中令y=1得：

在式（7）中令y=-1得：

将式（9）代入式（10）得 ：

步骤四：证明1＋f（x）=f（1＋x）。

通过计算得：

将式（8）代入式（12）得：

步骤五：证明f=δ，其中δ是域F上的自同构。

令δ=f，由式（11）得：

再由式（11）及式（13）得：

即

由式（14）及式（15）得δ是域F上的自同态，下面证明δ是单的。

由式（11）得：1=f（1）=f（aa-1）=f（a）f（a-1），∀a∈F＊，

故

若δ（a）=δ（b），应用式（6）、式（15）及式（16）得a=b。故δ是域F上的自同构。

同理，类似于情况一的方法，可证情况二时，f=-δ。

3 上三角矩阵空间上保持对合的函数

定理2 函数f是T n（F）（n≥4）上的保持对合的充要条件是f=±δ，其中δ是域F上的自同构。

证明 由于f是T n（F）（n≥4）上的保持对合的函数，故对∀A∈T n（F）⇒A f∈T n（F）⇒f（0）=0。

通过对定理1的证明可知，I n，C，D∈T n（F），故只需证明f（-t）=-f（t）及-2f（x）=f（-2x），可得f=±δ。

通过计算得：

在式（17）中令a=b=-1得 ：

在式（17）中令a=b=1得 ：

在式（17）中令a=-1得 ：

通过计算得：

假若f（-1）=0成立，将其代入式（19）得：f（2）=0，代入式（22）得：f（-t）=0，与f（1）=1矛盾，故f（-1）≠0。由式（18）得：f（2）≠0，代入式（21）得：f（-1）=-1。代入式（19）知f（2）=2。代入式（22）得：f（-t）=-f（t），再代入式（20）得：2f（b）=f（2b）。令b=-x代入上等式中得：f（-2x）=2f（-x）=-2f（x）。

／References：

［1］ YAO Hongmei，SONG Xiaocui，WANG Guanghui.A note on functions preserving some properties of matrices［A］.Proceeding of the Sixth International Conference of Matrices and Operators［C］.［S.l.］：［s.n.］，2011：77-80.

［2］ 樊玉环，王佩臣.域上上三角矩阵空间的保持幂等的函数［J］.河北科技大学学报，2013，34（3）：200-203.FAN Yuhuan，WANG Peichen.Function preserving idempotence of all upper triangular matrices over any field［J］.Journal of Hebei University of Science and Technology，2013，34（3）：200-203.

［3］ 张 显，曹重光.域上上三角矩阵空间保幂等与立方幂等的加法单映射［J］.数学杂志，2004，24（4）：416-420.ZHANG Xian，CAO Chongguang.Additive injective maps preserving idempotence and tripotence on the space of triangular matrices over fields［J］.Journal of Mathematics，2004，24（4）：416-420.

［4］ 佟 鑫，曹重光.域上从对称矩阵空间到全矩阵空间保幂等的线性算子［J］.黑龙江大学自然科学学报，2003，20（3）：25-28.TONG Xin，CAO Chongguang.Linear operators preserving idempotence from symmetric matrix spaces to all matrix spaces over a field［J］.Journal of Natural Science of Heilongjiang University，2003，20（3）：25-28.

［5］ CAO Chongguang.Linear operators that preserveM-Pinverses of matrices［J］.Northeast Mathematics Journal，1993，9（2）：255-260.

［6］ 张 显.交换整环上的上三角矩阵的保幂等的线性算子［J］.新疆大学学报，1993，10（2）：25-27.ZHANG Xian.Linear operators preserving idempotent on the upper triangular matrix over commutative domain［J］.Journal of Xinjiang University，1993，10（2）：25-27.

［7］ CHAN G，LIM M，TAN K.Linear preservers on matrices［J］.Linear Algebra Appl，1987，93：67-72.

［8］ LI C，PIERCE S.Linear preservers problems［J］.Am Math Mon，2001，108（7）：591-605.

［9］ 曹重光.实数域上有限可除代数矩阵空间保幂等的线性算子［J］.数学杂志，1992，12（3）：349-353.CAO Chongguang.Linear operators preserving idempotent on the finite division algebra matrix space over the real number field ［J］.Journal of Mathematics，1992，12（3）：349-353.

［10］ CAO Chongguang，ZHANG Xian.Additive operators preserving idempotent matrices over field and applications［J］.Lin Alg Appl，1996，248：327-338.

［11］ 曹重光.某些环上矩阵模的保幂等的线性映射［J］.黑龙江大学自然科学学报，1999，16（1）：1-4.CAO Chongguang.Linear maps preserving idempotent of matrix module over the some rings ［J］.Journal of Natural Science of Heilongjiang University，1999，16（1）：1-4.

［12］ MARCUS M.All linear operators leaving the unitary group invariant［J］.Duke Math J，1959，26（1）：155-163.

［13］ MARCUS M，WESTWICK R.Linear Maps on skew symmetric matrices：The invariance of elementary symmetric functions［J］.Pacific J Math Mon，1960，10：917-924.

［14］ 侯晋川，崔建莲.算子代数上线性映射引论［M］.北京：科学出版社，2002.HOU Jinchuan，CUI Jianlian.Introduction to linear maps on the operator algebras［M］.Beijing：Science Press，2002.

［15］ 张 显，曹重光.保不变量的矩阵加群同态［M］.哈尔滨：哈尔滨出版社，2001.ZHANG Xian，CAO Chongguang.Additive Operators Preserving Invariants［M］.Harbin：Harbin Press，2001.

［16］ 华罗庚，万哲先.典型群［M］.上海：上海科技出版社，1962.HUA Luogeng，WAN Zhexian.Classical Groups［M］.Shanghai：Shanghai Science and Technology Press，1962.