江卫华，刘秀君，宗慧敏

（1.河北科技大学理学院，河北石家庄 050018；2.河北化工医药职业技术学院基础部，河北石家庄050026）

1 问题提出

（k，n-k）共轭边值问题长期以来一直受到国内外很多专家学者的广泛关注，读者可参阅文献［1］-文献［9］。文献［1］-文献［6］在非共振条件下研究了整数阶（k，n-k）共轭边值问题解的存在性；文献［7］研究了具有共振的整数阶（k，n-k）共轭边值问题解的存在性；在非共振情况下，文献［8］与文献［9］研究了分数阶（n-1，1）共轭边值问题分别在局部和非局部边界条件下解的存在性。受上述文献启发，本文研究具有共振的分数阶（n-1，1）共轭边值问题：

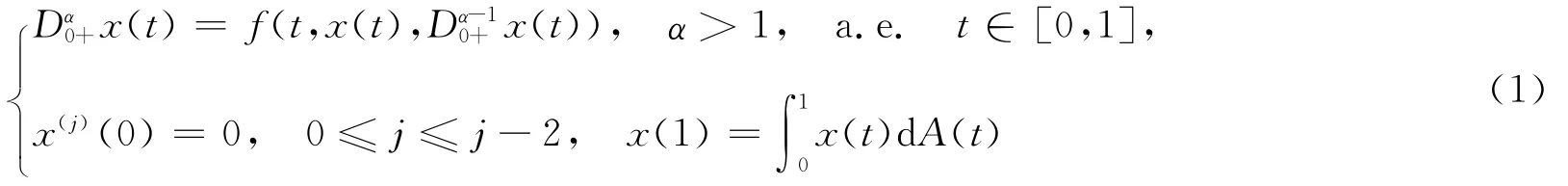
解的存在性，其中A（t）是［0，1］上的有界变差函数，n是大于或等于α的最小整数。

假设如下条件成立：

C1）f：［0，1］×R2→R关于L p［0，1］，1＜p＜＋∞ 满足S-Carathéodory条件，即：

1）对a.e.t∈ ［0，1］，f（t，·）在R2上连续；

2）对任意z∈R2，f（·，z）是［0，1］上的Lebesgue可测函数；

3）对任意r＞0，存在非负函数φr∈L p［0，1］使得：

2 预备知识

为了获得相应结论，首先给出几个概念和算子方程解的存在定理，见文献［10］。

设X，Y是实Banach空间，L：domL⊂C→Y是指数为零的Fredholm算子，P：X→X和Q：Y→Y是连续投影算子，且满足ImP=KerL，KerQ=ImL，X=KerL⊕KerP，Y=ImL⊕ImQ。由此可知L：domL∩KerP→ImL是可逆的，用K p表示它的逆。

定义1 设Ω为X的有界开子集，且domL∩Ω≠∅，算子N：X→Y，如果QN（）有界，且K p（I-Q）N（）是紧的，则称N在上是L-紧的。

定理1［10］设L是指数为零的Fredholm算子，N在上是L-紧的，假设下列条件成立：

1）Lx≠λNx，对任意（x，λ）∈ ［（domL＼KerL）∩∂Ω］×（0，1）；

2）Nx∉ImL，对任意x∈KerL∩∂Ω；

3）deg（QN｜KerL，Ω∩ KerL，0）≠0。

则Lx=Nx在domL∩上至少有1个解。

以下定义和引理参见文献［11］和文献［12］。

定义2 函数y：［0，1］→R的α阶分数阶积分定义为

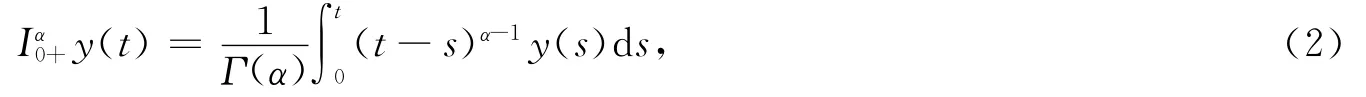
其中α＞0，右端被积函数在［0，1］区间逐点可积。

定义3 函数y：［0，1］→R的α阶分数阶导数定义为

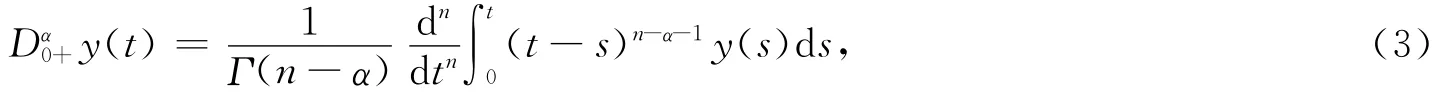
其中α＞0，右端被积函数在［0，1］区间逐点可积且可导，n=［α］＋1。

引理1 设f∈L1［0，1］，q≥p≥0，q＞1，则

引理2 设α＞0，λ＞-1，则

其中n是大于或等于α的最小正整数。

易证下述不等式成立：

引理4 对 任意b＞a＞0，p≥1，有（b-a）p≥bp-ap。

3 主要结果

假设条件C1）和条件C2）成立。

取空间X=Cα-1［0，1］= ｛x｜x，Dα0-＋1x∈C［0，1］｝，范数定义为｝，其中｜。由文献［13］知，（X，‖·‖）是Banach空间，取空间Y=L p［0，1］，范数定义为，其中p同条件C1）。

定义线性算子L：domL⊂X→Y如下：

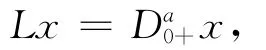
其中：

定义非线性算子N：X→Y如下：

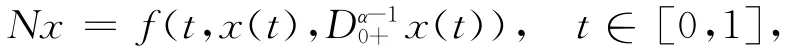
则算子方程Lx=Nx，x∈domL的解即为边值问题（1）的解。

引理5 设条件C1）和条件C2）成立，则L：domL⊂X→Y是指数为零的Fredholm算子，且投影算子Q：Y→Y及算子L：domL∩KerP→ImL的逆算子K p分别为

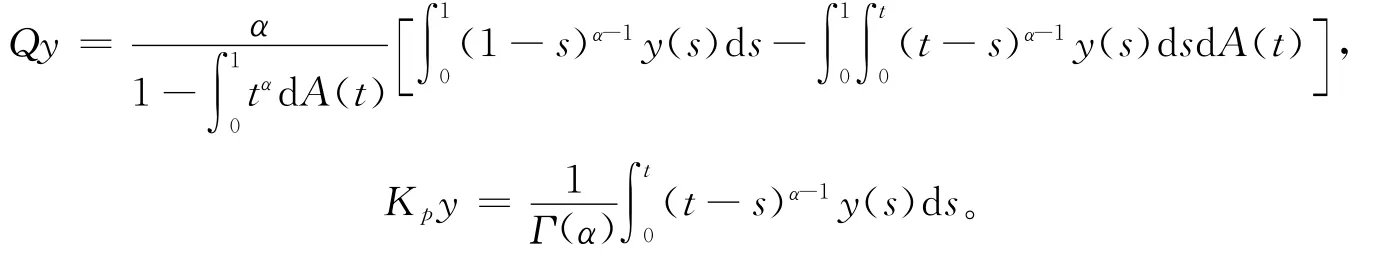
证明 易 知KerL= ｛ctα-1｜c∈R｝。定义算子P：X→X为。通过简单计算可得P2x=Px，x∈X，且ImP=KerL，X=KerL⊕KerP。

由Lx=y，x∈domL可得y满足：

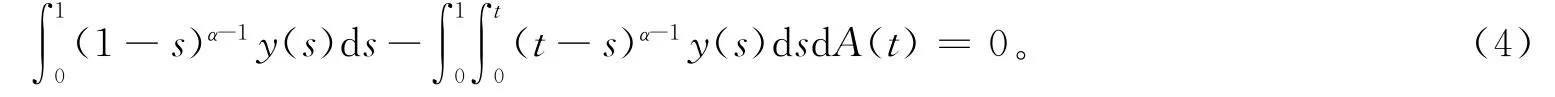
反之，若y满足式（4），取x（t）

易证x∈domL，且Lx=y。从而可得：

显然KerQ=ImL，通过简单计算可得Q2y=Qy，y∈Y。

任取y∈Y，由y=（y-Qy）＋Qy知Y=ImL＋ImQ。取y∈ImL∩ImQ，由y∈ImQ得y=Qy，由y∈ImL=KerQ得Qy=0，因此y=0。所以有Y=ImL⊕ImQ。从而dim KerL=dimY／ImL=1，即：L是指数为零的Fredholm算子。

取y∈ImL，容易验证K p y∈domL∩KerP且LK p y=y。反之，若x∈domL∩KerP，则

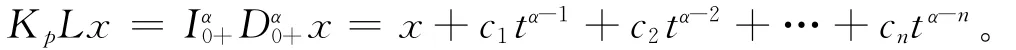
由x，K p Lx∈domL∩KerP，可得c1=c2= … =cn=0。从而有K p Lx=x。即

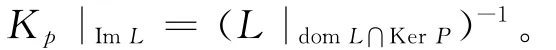
引理6 设Ω是X的有界开子集，且domL∩Ω≠∅，则N在上是L-紧的。

证明 因Ω有界，存在常数r＞0，使得‖x‖≤r，x∈，由条件C1），存在函数φr∈Y，使得：

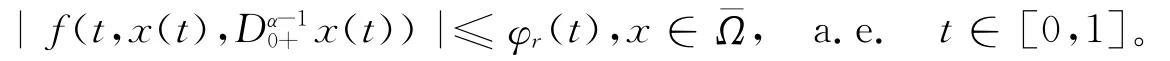
取x∈，则有

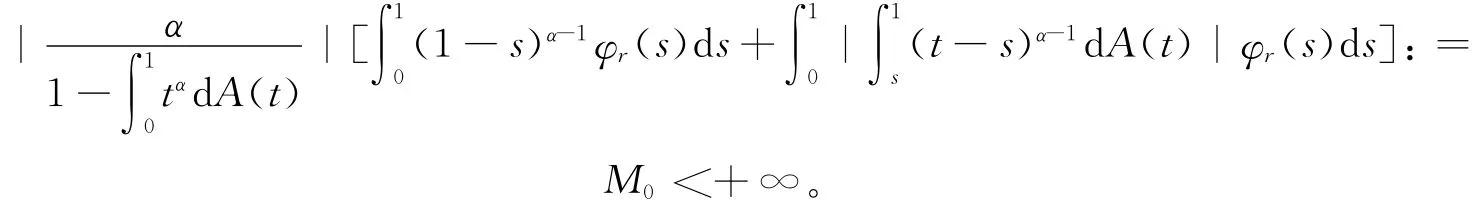
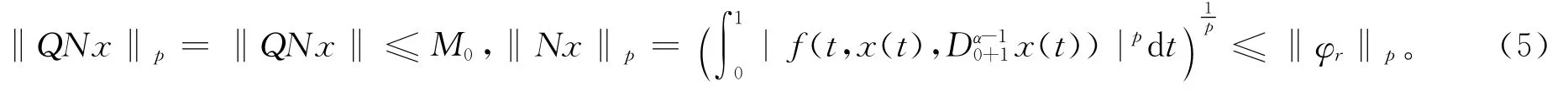
由式（5）以及Holder不等式可得：

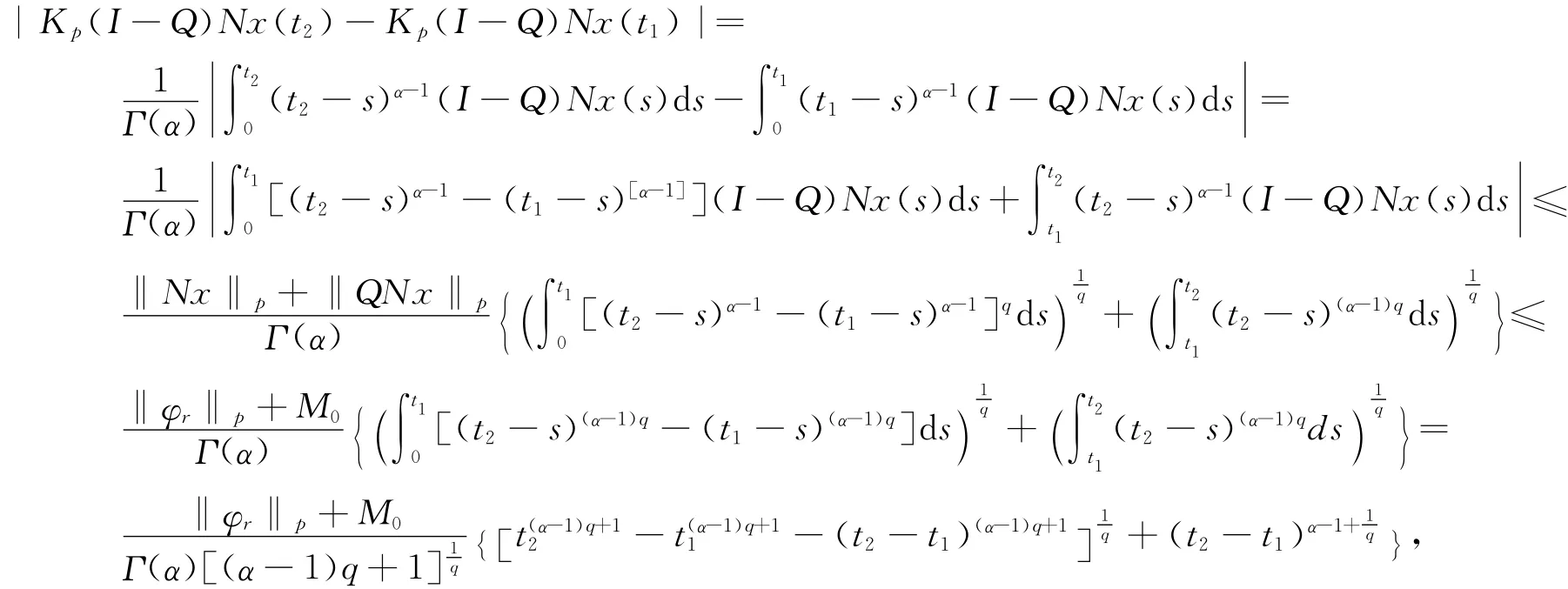
由t（α-1）q＋1和t在［0，1］上的一致连续性可得Kp（I-Q）N（）是等度连续的。

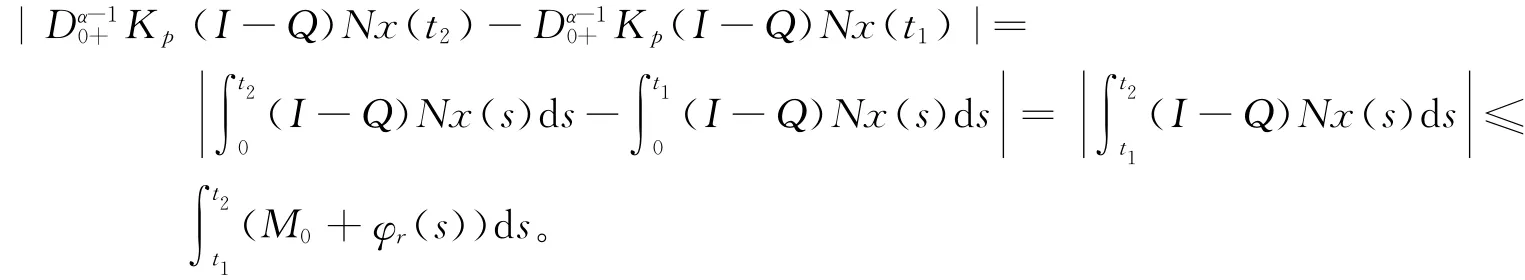
因为φr∈Y⊂L1［0，1］，由积分的绝对连续性可得Kp（I-Q）N（）是等度连续的。由Arzela-Ascoli定理知Kp（I-Q）N（）是紧的。

定理2 设条件C1）和条件C2）成立，并假设下列条件成立：

H1）存在常数M ＞ 0使得当x∈X，｜｜＞M，∀t∈ ［ 0，1］时，QNx ≠ 0。

H2）存在非负函数a（t），b（t），c（t）∈L1［0，1］使得：

其中 ‖c‖1＜1，‖b‖1＜Γ（α）（1-‖c‖1）。

H3）存在常数M＊＞0，如果｜c｜＞M＊，那么下列不等式之一成立：

1）cQN（ctα-1）＞0，

2）cQN（ctα-1）＜0。

为证明该结论，首先证明如下3个引理。

引理7 假设条件H1）和条件H2）成立，则下述集合有界：

证明 任 取x∈Ω1，则有Lx=λNx，从而Nx∈Im L=Ker Q。由条件H1）可知，存在t0∈ ［0，1］，使得｜≤ M 。又由Lx=λNx 得 ：

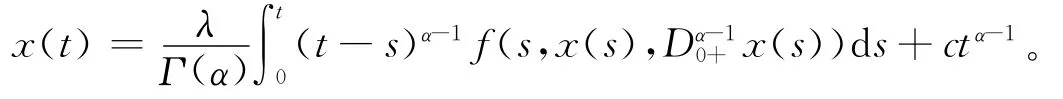
两边求α-1阶导数，得：

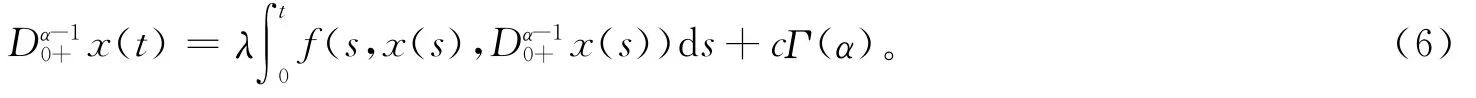
代入t=t0，得：

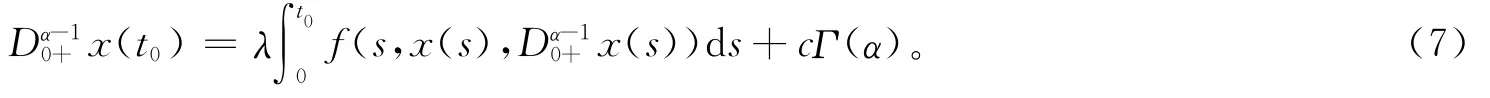
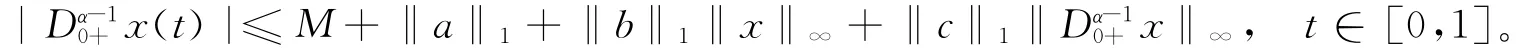
由此可得：

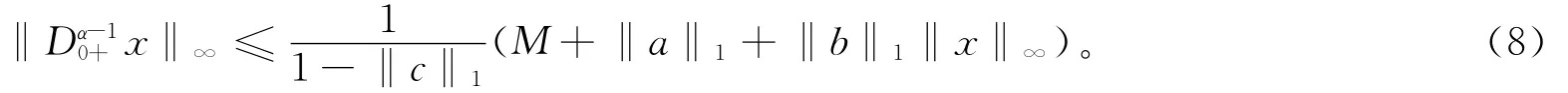
由于x（t）=且x j（0）=0，0≤j≤n-2，所以有c1=c2= … =cn-1=0，即

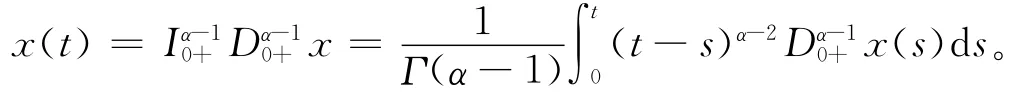
因此有：

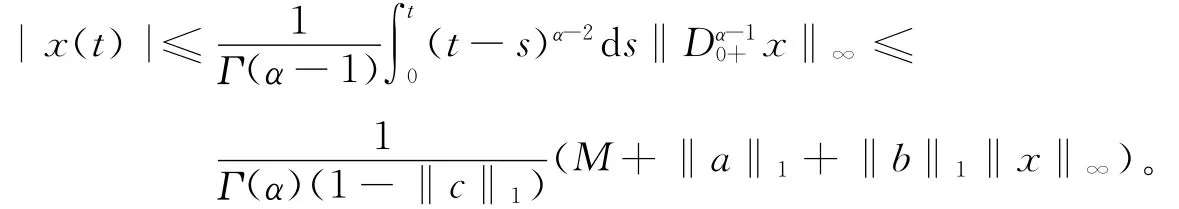
从而可得：

由式（8）和式（9）知Ω1有界。

引理8 设条件H1）成立，则集合Ω2=｛x∈KerL｜Nx∈ImL｝有界。

证明 由x∈Ω2可知x=ctα-1且QNx=0。由条件 H1）可得｜x（t）｜=Γ（α）｜c｜≤M。所以有因此Ω2有界。

引理9 设 条件 H1）和条件 H3）成立，则集合Ω3= ｛x∈KerL｜λθJx＋（1-λ）QNx=0，λ∈ ［ 0，1］｝有界，其中

证明 任 取x∈Ω3，则x=ctα-1且 满足λθJ（ctα-1）＋（1-λ）QN（ctα-1）=0。如果λ=1，则c=0；如果λ=0，则QN（ctα-1）=0，由引理8的证明过程可得如果λ∈ （ 0，1），则有：

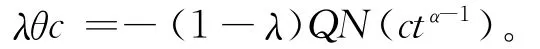
假设｜c｜＞M＊，由条件 H3）可得：λc2=-（1-λ）θcQN（ctα-1）＜0。

与已知矛盾。因此｜c｜≤M＊，即Ω3有界。

定理2的证明。

1）Lx≠λNx，对任意（x，λ）∈ ［ （domL＼KerL）∩∂Ω］× （0，1）；

2）Nx∉ImL，对任意x∈KerL∩∂Ω；

下面证明deg（QN｜KerL，Ω∩KerL，0）≠0。

令H（x，λ）=λθJx＋（1-λ）QNx。由引理9知H（x，λ）≠0，x∈KerL∩∂Ω。由度的同伦不变性可得：

由定理1，Lx=Nx在domL∩上至少有1个解，此即为问题（1）的解。

例 考虑如下分数阶微分方程解的存在性：

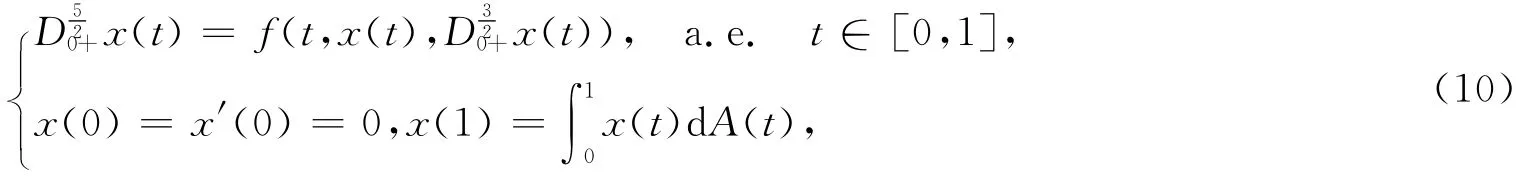
其中

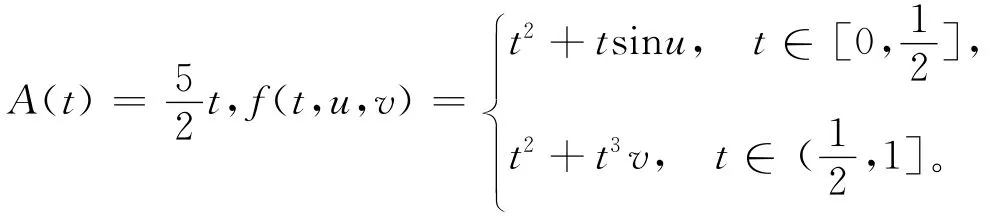
对应问题（1），α=。取φr（t）=t2＋t＋rt3，a（t）=t2＋t，b（t）=0，c（t）=t3，M=M＊=45。通过简单计算可得问题（10）满足定理2的所有条件，因此边值问题（10）至少有1个解。

／References：

［1］ ELOE P W，HENDERSON J.Positive solutions for（n-1，1）conjugate boundary value problems［J］.Nonlinear Anal，1997（28）：1669-1680.

［2］ ELOE P W，HENDERSON J.Singular nonlinear（k，n-k）conjugate boundary value problems［J］.J Differential Equations，1997（133）：136-151.

［3］ AGRWAL R P，O＇REGAN D.Multiplicity results for singular conjugate，focal，and （N，P）problems［J］.J Differential Equations，2001（170）：142-156.

［4］ ELOE P W，AHMAD B.Positive solutions of a nonlinear n-th order boundary value problem with nonlocal conditions［J］.Appl Math Lett，2005（18）：521-527.

［5］ JIANG W.Multiple positive solutions fornth-orderm-point boundary value problems with all derivatives［J］.Nonlinear Anal，2008（68）：1064-1072.

［6］ WEBB J R L.Nonlocal conjugate type boundary value problems of higher order［J］.Nonlinear Anal，2009（71）：1933-1940.

［7］ JIANG W.Solvability of（k，n-k）conjugate boundary-value problems at resonance，Electron［J］.J Differential Equations，2012（12）：1-10.

［8］ WANG Y，LIU L，WU Y.Positive solutions for nonlocal fractional differential equations［J］.Nonlinear Anal，2011（74）：3599-3605.

［9］ YUAN C.Multiple positive solutions for（n-1，1）-type semipositive conjugate boundary value problems of nonlinear fractional differential equations，Electron［J］.J Qual Theory differ Equ，2010，（10）：1-12.

［10］ MAWHIN J.Topological degree methods in nonlinear boundary value problems，in：NSFCBMS regional conference series in mathematics［J］.Amer Math Soc Providence，RI.1979（15）：28-39.

［11］ PODLUBNY I.Fractional Differential Equations［M］.New York：Acatdemic Press，1999.

［12］ MILLER K S，ROSS B.An Introduction to the Fractional Calculus and Fractional Differential Equations［M］.New York：Wiley，1993.

［13］ JIANG W.The existence of solutions to boundary value problems of fractional differential equations at resonance［J］.Nonlinear Anal，2011（74）：1987-1994.