包丙寅

（内蒙古师范大学 数学科学学院 内蒙古 呼和浩特 010010）

实数基本定理的等价性证明

包丙寅

（内蒙古师范大学 数学科学学院 内蒙古 呼和浩特 010010）

实数基本定理的内容及其等价性证明是数学分析课程中的难点和重点.本文全方面的给出了确界原理、单调有界原理、区间套定理、有限覆盖定理、致密性定理、柯西收敛原理这六个实数基本定理的等价性证明.

确界原理；单调有界原理；区间套定理；有限覆盖定理；致密性定理；柯西收敛原理；等价性

实数基本定理的内容：

（1）（确界定理）任何非空集E奂R，若它有上界，则必有上确界s u p E∈R；等价地若有下界，必有下确界.

（2）（单调有界原理）任何单调递增、有上界的序列{xn}奂 R，必有极限；等价地，单调递减、有下界也必有极限.

（3）（柯西收敛原理）序列{xn}奂R收敛的充要条件是：坌ε＞0，埚N＞0，当m,n＞N时，有|xn-xm|＜ε.

（4）（致密性定理）有界序列必有收敛的子序列.

（5）（区间套定理）任何闭区间套，必存在唯一的公共点.即：若an↗，bn↘，an≤bn，bn-an→0（当n→∞时），则{[an,bn]}成为闭区间套，这时必存在唯一的ξ∈R，使得an≤ξ≤bn，（坌n∈R）.

（6）（有限覆盖定理）闭区间上的任一开覆盖，必存在有限开覆盖.即:设{△}是一个开区间，若坌x∈[a,b]，埚△x∈{△}，使得x∈△x，则称{△}为闭区间[a,b]的一个开覆盖.定理指出，[a,b]的任一开覆盖{△}中，必存在有限子集{△1,△2,…,△r}奂{△}，{△1,△2,…,△r}仍为[a,b]的一个开覆盖.

1 利用区间套定理证明其他实数基本定理

1.1 利用区间套定理证明有限覆盖定理

证[1]：假设某一闭区间[a,b]的某个开覆盖{△}无有限子覆盖，将[a,b]二等分，则至少有一“半区间”，它不能用{△}的有限子集覆盖，将此半区间记为[a1,b1]（如果两个半区间都如此，可任选其中的一个）.然后将[a1,b1]再二等分，重复上述步骤，无限进行下去，便得一区间套{[an,bn]}：an↗，bn↘，bn-an=（b－a）→0（当n→∞时）,每个[an,bn]都不能用{△}的有限个覆盖.利用区间套定理，可知存在一点ξ，为[an,bn]的唯一公共点.则ξ点处产生矛盾，因为一方面ξ∈[a,b]，所以存在一开区间△1=（α,β）∈{△}使得α﹤ξ﹤β，但由于,所以n充分大时有a﹤an≤ξ≤bn﹤β，这表明[an,bn]已被△1=（α,β）∈{△}所覆盖.与[an,bn]的本性矛盾.

1.2 利用区间套定理证明致密性定理

证[11]：设{yn}为有界数列，即埚a，b使a≤yn≤b.等分区间[a,b]为两个区间，则至少有一个区间含有{yn}中的无穷个数.把这一区间记为[a1,b1]，如果两个区间都含有无数个yn，则任取其一作为[a1,b1].然后将[a1,b1]再二等分，重复上述步骤，无限进行下去，便得一区间套a）→0（当n→∞时）,利用区间套定理，可知存在唯一一点ξ，为[an,bn]的唯一公共点使an→ξ，bn→ξ，且ξ∈[ak,bk]，（k=1，2，…）.每一[ak,bk]中均含有{yn}中的无穷个数.在[a1,b1]中任取{yn}中的一项记为yn1，即{yn}的第n1项.

因为[a2,b2]也含有无穷个yn，则它必含有yn1以后的无穷多个数,在这些数中任取其一记为yn2,n2﹥n1,继续在每一个[ak,bk]中都这样取一个数ynk,即得{yn}的一个子列{ynk},其中n1﹤n2﹤…且ak≤ynk≤bk.因为ak→ξ（当k→∞时）,bk→ξ（当k→∞时）,所以ynk→ξ（当k→∞时）.

1.3 用区间套定理证明确界定理

证[1]：设M为集合E奂R的上界（即对任意x∈E有x≤M），来证明埚ξ=s u p E∈R.若E有最大值，则最大值即为上确界.现设E无最大值.任取一x0∈E，将[x0,M]二等分，若右半区间含有E中的点，则记右半区间为[a1,b1],否则就记左半区间为[a1,b1].然后将[a1,b1]再二等分，用同样的方法选记[a2,b2]，如此无限下去，我们便得一区间套{[an,bn]}：an↗，bn↘，bn-an=（M－x0）→0（当n→∞时）,利用区间套定理，可知存在一公共点ξ∈[an,bn]，ξ正是E的上确界.

1.4 利用区间套定理证明单调有界原理

证[1]：设{xn}是单调上升有上界的实数列.b是它的一个上界，令a=x-1，二等分[a,b]其中必有一区间含有{xn}中的无穷多项，记其为[a1,b1].然后将[a1,b1]再二等分，用同样的方法选记[a2,b2]，如此无限下去，我们便得一区间套{[an,bn]},满足[an,bn]含{xn}中的无穷多项.由闭区间套定理可得，埚唯一的r∈和{bn}的极限都是r.则对坌ε﹥0埚n，坌n﹥N,有

r-ε﹤a≤b﹤r+ε.取n﹥N，[a,b]中含{xn}中的无穷多项，则埚M，使xn∈[a,b].当m﹥M时，有xm∈[a,b].如果不然，埚m﹥M，有b﹤xm，则在[a,b]中最多含{xn}中的前m项，与[a,b]的构造矛盾.从而当m﹥M时，有r-ε﹤a≤x≤b﹤r+ε,即|x-r|﹤ε所以{xn}，{xm}的极限为r，即{xn}的极限为r.

1.5 利用区间套定理证明柯西收敛准则

证[3]：充分性.设{xn}为基本数列，因此它有界，从而有常数a1，b1满足条件，a1≤xn≤b1，n∈N+，将[a1,b1]三等分，令C1=得到三个长度相同的子区间[a1,c1]，[c1,c2]，[c2,b1]，分别记为J1，J2，J3，据它们在实数轴上的左，中，右位置和基本数列的定义即可发现：在左边的J1和右边的J3中，至少有一个子区间只含有数列{xn}中的有限项.这从几何上看是很直观的，若在J1和J3中都有数列中的无穷多项，则可以在J1中取xn，在J3中取xm使得n,m都可以任意大，同时满足不等式≥（b-a）这与{xn}为基本数列的条件矛盾，所以可以从[a1,b1]去掉只含有数列{xn}中有限项的子区间J1和J3（若两个子区间都是如此则任取其一）将得到的区间记为[a2,b2]，复上述步骤，无限进行下去，便得区间套{ [ak,bk]}且满足1'闭区间套中的每个区间长度是前一个区间长度的,2'每一个[ak,bk]中含有数列{xn}中从某项起的所有项.性质1'保证存在ξ是{ak}，{bk}从两侧分别单调的收敛与ξ.现只需证明ξ即基本数列{xn}的极限.坌ε﹥0，埚N∈N，使aN，bN进入点ξ的ε邻域，即有[aN,bN]奂（ξ-ε,ξ+ε）因为[aN,bN]具有性质2'所以埚N1当n﹥N1时成立|xn-ξ|﹤ε.

必要性.设an→a（当n→∞时），则坌ε﹥0，埚N∈N，当k﹥N时，有

|xn-a|﹤，从而当n，m﹥N时，有

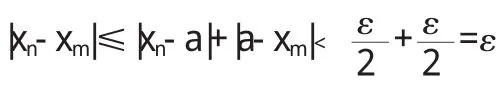
2 利用有限覆盖定理证明其他实数基本定理

2.1 利用有限覆盖定理证明确界定理

证[1]：设E不是空集，且E奂R，任意x∈E有x≤M.任取一点x0∈E，考虑闭区间[x0,M]，假若E无上确界﹙最小上界﹚，则对任意x∈[x0,M)：

（1）当x为E的上界时,必有更小的上界x1﹤x，因而x有一个开领域△x，其中都为E的上界；

（2）当x不是E的上界时,自然有E中的点x2﹥x，于是x有开领域△x，其中每个点都不是E的上界.

（3）[x0,M]上每点都找出一个领域△x，它要么属于第一类（每点为上界），要么属于第二类（每点都不是上界）.这些领域{△x：x∈[x0,M]，组成闭区间[x0,M]的一个开覆盖，由有限覆盖定理，必存在有限子覆盖{△1，…，△n｝.注意，M所在的开区间，因为第一类的，相邻接的开区间有公共点，也应为第一类的，经过有限次邻接，可知x0所在的开区间也是第一类的.这便得出矛盾.

2.2 利用有限覆盖定理证明区间套定理

证：设{[an,bn]}是满足区间套定理两个条件的闭区间列，证

先证明这一列闭区间开交不等于空集.用反证法，设[an,bn]为空集，则对任意x∈[a1,b1]，x埸，所以存在nx，使得x埸，当n≥nx时x埸[an,bn]，所以存在δx﹥0，当n≥nx时（x-δx,x+δx）∩[an,bn]为空集，令G=｛（x-δx,x+δx）x∈[a1,b1]｝则G覆盖[a1,b1]，所以存在G中有限个开区间（x-δxi,x+δxi）覆盖[a1,b1]对每一个i（i=1，…，k）存在nxi，当n≥nxi时，（xi-δxi,xi+δxi）∩[an,bn]为空集，令N=m a x{nxi|i=1，…，k}则 n﹥N时为空集，这与[a1,b1

（xi-δxi,xi+δxi）矛盾，所以 不为空集，因为bn-an→0（当n→∞时），所以只有一个元素，所以

2.3 利用有限覆盖定理证明致密性定理

证[4]：{xn}为有界数列，a是它的一个下界，b是它的一个上界，于是下列两种情况之一成立：

（1）存在α∈[a,b]，使α在任何邻域中都有{xn}的无穷多项；

（2）对任何x∈[a,b]，都存在x的一个邻域（x-δx,x+δx），使其中只含{xn}的有限多项.

如果（2）成立，则开区间族{（x-δx,x+δx）x∈[a,b]}构成[a,b]的一个开覆盖.所以其中必有有限子覆盖.由于每个开区间中都只含{xn}的有限多项，故有限个开区间之并也只含{xn}的有限多项.但另一方面又应该包含{xn}的所有项，矛盾.则（2）不成立，即必是（1）成立.

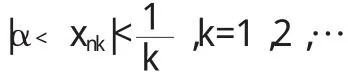
当然xnk→α（当k→∞时）即{xnk}为{xn}的收敛子列.

2.4 利用有限覆盖定理证明单调有界原理

证：用反证法.若不然，多任意x∈[a,b]，x都不是{an}的极限，则对任意x∈[a,b]，埚δx使胰(x,δx)内至多含有{an}的有限项，作开区间集，然后由有限覆盖定理推出矛盾.

2.5 利用有限覆盖定理证明柯西收敛准则

证[8]：设点列{xn}为柯西列，因此它有界，证若{xn}有子列收敛则{xn}收敛.设{xnk}奂{xn}，xnk→x0（当k→∞时）存在，即ε﹥0埚N﹥0当k﹥N时成立，|xnk﹤x0|<ε由{xn}为柯西列，所以对上面的ε﹥0埚N1当m,n﹥N1时成立|xn-xm|﹤ε，所以k充分大时有|xn-x0|≤|xnk-xn|+|xnk-x0|﹤2 ε.下面证明{xn}有收敛子列，不妨设当n≠m，xn≠xm否则{xn}有收敛子列是显然的，由于{xn}有界，所以埚M﹥0{xn}奂[-M,M]，若{xn}没有收敛子列，x∈[-M,M]，埚εx﹥0使Ix=﹙x-εx，x+εx﹚至多包含{xn}中的一个点，而[-M,M]由有限覆盖定理知埚x1，…，xN∈ [-M,M]满足，所以{xn}中只有有限个元素，矛盾.

3 利用单调有界定理证明其他实数基本定理

3.1 利用单调有界定理证明区间套定理

证[5]：设{[an,bn]}为一区间套.由区间套定义，an↗，并以bn为其上界，因而存在an→ξ（当n→∞时），且an≤ξ，n=1，2，…同理，bn↘，则数列{bn}的极限为数列{bn-an}的极限与数列{an}的极限和，所以bn→ξ≤bn（当n→∞时），n=1，2，….

这样就得ξ∈[an,bn]，n=1，2，….

最后证明上述ξ是唯一的.倘若另有一数ξ'∈[an,bn]，n=1，2，…，则由|ξ-ξ'|≤bn-an|→0（当n→∞时）推知ξ=ξ'.

3.2 利用单调有界定理证明确界原理

证[2]：设数集X={x}有上界M且X非空，则埚x1∈X，令记M为M1，有x1≤M1若x1=M1，则M1为上确界，若x1﹤M1则记a=M1-x1现用等分区间法来构造两个数列，令y1=（M1+x1）

分两种情况1'y1为X的上界则记它为M2若y1∈X则y1即X的上确界，否则y1埸X记x2=x12'y1不为X的上界，则埚x2∈X使x2﹥y1若x2是X的上界，则它就是X的上确界，否则记M2=M1,所以或定理得证或x1≤x2﹤M2≤M1且x2∈M2的a邻域﹙因为M2-x2≤（M1-x2）=a以x2，M2代替x1，M1重复上述步骤得x3，M3不断重复得或者到某一部定理得证，否则构造的两个数列{xn}，{Mn}他们有x1≤x2≤…≤xn≤…﹤…﹤Mn≤…M2≤M1其中xn∈X,Mn为X的上界且xn∈Mn的邻域，所以{Mn}是一广义单调下降且有下界数列.由单调有界原理知它有极限M0.最后证明M0是X的上确界.先证M0是X的上界,因为x∈X都有x≤Mn（当n→∞时）取极限得x≤M0即M0是X的上界.再证M0是X的上界中的最小的ε﹥0埚N1,当n﹥N1时有{Mn}全属于M0的ε邻域埚n0使n0﹥N1且（这一不等式成立是因为a是一无穷小量）所以xn即属于Mn0的邻域，当然属于Mno的邻域，即xn0﹥M0-ε（所以M0是X的上确界.

3.3 利用单调有界定理证明有限覆盖定理

证：用反证法.若[a,b]没有有限覆盖，对[a,b]采用二等分的方法，构造两个数列{an},{bn}，其中[an,bn]没有有限覆盖，且{an},{bn}单调，得出矛盾.

3.4 利用单调有界定理证明柯西收敛准则

证：首先证明有界数列{an}有单调子数列.an有性质M，若对每个i﹥n，都有an≥ai，也就是说，an是集合｛ai｜i﹥n｝的最大数。分两种情况讨论：﹙a﹚数列{an}有无穷多项具有性质M，将他们按下标的顺序排列，记为an1，…ank,…满足n1﹤…﹤nk﹤…,则我们就已经得到一个单调下降的子列{ank}.﹙b﹚数列{an}只有有穷多项具有性质M，则埚N,当n﹥N时，有an不具有性质M，即埚i﹥n，有an﹤ai从中任取一项记为an1，因为它不具有性质M，所以埚n2﹥n1，使an1﹤an2﹤…，如此继续下去，我们得到一子列{ank}单调上升，所以有界数列{an}有单调子数列，由单调有界定理，可得{ank}存在极限.

4 利用确界原理证明其他实数基本定理

4.1 利用确界原理证明单调有界定理

证[5]：不妨设{an}为有上界的递增数列.由确界原理，数列{an}有上确界，记a=s u p{an}.下面证明a就是{an}的极限.事实上，任给ε﹥0，按上确界的定义，存在数列{an}中某一项aN，使得a-ε﹤aN.又由{an}的递增性，当n≥N时有a-ε﹤aN≤an.另一方面，由于a是{an}的一个上界，故对一切an都有an≤a﹤a＋ε.所以当n≥N时有a-ε﹤an﹤a＋ε,这就证明了结论.同理可证有下界的递减数列必有极限,且其极限即为它的下确界.

4.2 利用确界原理证明区间套定理

证明：由定理的条件立即知道an↗且有上界，bn↘且有下界，由确界原理知数列{an}的极限存在，且极限等于{an}的上确界.通理{bn}的极限存在，且极限等于{bn}的下确界.亦即对任何正整数k，有

由定理的另一个条件：bn-an→0（当n→∞时）,并且由于{an}及{bn}的极限都存在，则有数列{bn-an}的极限等于数列{bn}的极限与数列{an}的极限差，等于0.

从而证明了两个极限相等，且设ξ是它们的同一极限.于是定理前一部分的结果即已证得.剩下要证的是ξ是所有区间的唯一公共点.由﹙1﹚的两个不等式，即有

也就是ξ是所有区间的一个公共点.现在要证明ξ是唯一公共点.设除点ξ外，所设区间列还有另一个公共点ξ'，且ξ≠ξ'.由于an≤ξ，ξ'≤bn﹙n=1，2，…﹚故有

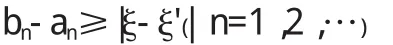
由数列极限的性质知，数列{bn-an}的极限为0，故有

4.3 利用确界定理证明有限覆盖定理

证[7]：令D=｛t:a≤t﹤b,[t,b]能被E中的有限个开区间覆盖，若我们证明a∈D则定理就得以证明.首先，证明D不是空集.因为劢[a,b],所以b必属于E中某个区间，记为﹙α, β﹚，任取t0满足a﹤t0﹤b,则[t0,b]奂﹙α,β﹚，这表示[t0,b]可以被E中的一个开区间覆盖.从而t0,∈D，这就证明了D不是空集.因为D总是包含在[a,b]中的，所以D是有界集，所以由确界存在定理知D有下确界，η=i n f D，因为a是D的下界，所以a≤η.第二部，证明a＝η，实际上若η﹥a由η∈[a,b]奂所以η必属于E中某个区间，记为﹙α',β'﹚从而有α'﹤ η﹤β'.由η是D的下确界，所以[η,β']中必存在某个t'∈D，现在，在﹙α',η﹚中任取一个t0∈[a，b﹚﹙η﹥a，这样的t0总是存在的﹚由[t0,t']奂﹙α',β'﹚∈E[t'，b]可以被E中的有限个开区间覆盖，所以t0∈D,所以t0≥η=i n f D这和t0∈﹙α',η﹚矛盾，所以a=i n f D最后证a∈D.因为a∈[a,b知E中存在开区间，记﹙α",β"﹚，使α"﹤a﹤β",因为a=i n f D,所以在﹙a,β"﹚中必存在t"∈D因为[a，t"]奂﹙α",β"﹚，[t"，b]可以被E中的有限个开区间覆盖所以[a,b]=[a，t"]∪[t"，b]可被E中的有限个开区间覆盖所以a∈D.

4.4 利用确界定理证明致密性定理

证:设数列{xn}是有界数列.定义数集A=｛x|{xn}中大于x的点有无穷多个｝因为{xn}有界所以A有上界且非空.由确界定理可得存在r，使r=s u p A，则ε﹥0有r-ε不是A的上界.所以{xn}中大于r-ε的项有无穷多个.因为r+ε是A的上界，所以{xn}中大于r+ε的项只有有限项.所以在﹙r-ε，r+ε﹚中有{xn}的无穷多项，即ε﹥0，n，埚n﹥N，使xn∈﹙r-ε，r+ε﹚对ε=1，埚n1，使xn∈﹙r-1，r+1﹚，即|xn-r|﹤1.取ε=，埚n2﹥n1，有|xn-r|﹤，如此继续下去，取ε=，埚nk﹥nk-1，有|xn-r|﹤，由此得到{xn}的子数列{xnk}，{xnk}的极限是r，所以{xn}存在

收敛子列.

4.5 利用确界定理证明柯西收敛准则

证：设{an}为柯西列，则易证{an}有界，由确界{an}存在定理，设，则ξ即为an的极限.

5 利用柯西收敛准则证明其他实数基本定理

5.1 利用柯西收敛准则证明区间套定理

证[3]：设{[an,bn]}是满足区间套定理两个条件的闭区间列，容易知道an↗，bn↘，an≤bn﹙n，m=1，2，…﹚所以对任意n∈N，任意p∈N，有|an+p-an|=an+p-an≤bn-an；且对ε﹥0，埚N∈N，n﹥N：0≤bn-an≤ε。对于上述的ε与N，n﹥N，p∈N时有|an+p-an|﹤ε，由柯西收敛准则知数列收敛，记an→ζ﹙当n→∞时﹚则数列{bn}的极限为数列｛bn-an｝的极限与数列{an}的极限和，所以bn→ζ﹙当n→∞时﹚.由an↗，bn↘知ζ∈[an,bn].

最后证明上述ζ是唯一的.倘若另有一数ζ'∈[an,bn]，n=1，2，…，则由|ζ-ζ'|≤bn-an→0﹙当n→∞时﹚推知ζ=ζ'.

5.2 利用柯西收敛准则证明单调有界定理

证[5]：设{an}为有上界M的递增数列.用反正法﹙借助柯西准则﹚可以证明：若{an}无极限，则可找到一个子列{ank}以+∞为其广义极限，从而与{an}有上界相矛盾.现在来构造这样的{ank}.

首先，对于单调数列{an}而言，柯西条件可改述为：“ε﹥0，埚N∈N，当n﹥N时，满足|an-aN|﹤ε”.这是因为它同时保证了对一切n﹥m﹥N，恒有|an-am|≤|an-aN|﹤ε.

由于假设{an}无极限，故由上述柯西条件的否定陈述，必存在某个ε0﹥0，对无论多大的N，均有某个n﹥N，使|an-aN|=an-aN≥ε0.依次取

把k个不等式相加,得到ank-ank-1≥k ε0.由此易知，当k﹥时，可使ank﹥M，矛盾.所以单调有界数列必有极限.

5.3 利用柯西收敛准则证明确界原理

证[3]：设S是一个有上界的集合.取实数b1，使对所有x∈S,都有x﹤b1.取a1∈S并考察区间[a1,b1]的中点，若是S的上界，则令a2=a1，b2=；若不是S的上界，则令.于是总可得到区间[a2,b2]，使b2是S的上界.[a2,b2]中有S的点且b2-a2=﹙b1-a1﹚.

再对闭区间[a2,b2]进行同样的处理，又可得到闭区间[a3, b3]奂[a2,b2]，使得b3是S的上界，[a3,b3]中有S的点且b3-a3=﹙b2-a2﹚=﹙b1-m a1﹚.继续这个过程，可得到一个闭区间的序列{[an,bn]}，满足下列条件：

﹙1﹚[an+1,bn+1]奂[an,bn]，n=1，2，…；

﹙2﹚bn-an=﹙b1-a1﹚，n=1，2，…；

﹙3﹚对每个n∈N，bn是S的上界且[an,bn]∩S≠空集，由﹙1﹚和﹙2﹚知，当m﹥n时有|bm-bn|=bm-bn﹤bn-an=﹙b1-a1﹚，可见{bn}为柯西列，由柯西收敛原理知{bn}收敛，设{bn}的极限为M.任意x∈S和任意n∈N，均有x≤bn，所以x≤M即M为S的上界.另一方面，对ε﹥0，由于｛bn-an｝的极限为0，所以有n0使bn0-an0﹤ε，又因为bn0≥M,所以，an0﹥bn0-ε≥M-ε，由﹙3﹚知[an0,bn0]中有S的点，这表明M-ε不是S的上界，所以S是M的上确界，所以﹙2﹚成立.

5.4 利用柯西收敛准则证明有限覆盖定理

证：用反证法.若[a,b]没有有限覆盖，对[a,b]采用二等分方法构造数列{an}和{bn}，[an,bn]没有[an,bn]有限覆盖，{an}和{bn}为柯西列，从而收敛且则ξ∈[a,b]由极限的局部保号性及[an,bn]的构造推出矛盾.

5.5 利用柯西收敛准则证明致密性定理

证：设数集A非空有上界，b1是A的上界，a1不是A的上界，a1﹤b1，用a1，b1的中点(a1+b1)二等分[a1,b1]，若(a1+b1)是A的上界，则取[a2,b2]=[a1(a1+b1)]，如果(a1+b1)不是A的上界，则取[a2,b2]=[(a1+b1)，b1]，用(a1+b1)二等分[a2, b2]，如此继续下去的数列，{an}，{bn}满足n，an不是A的上界，bn是A的上界且｛bn-an｝的极限为0.下证{an}是柯西列。因为｛bn-an｝的极限为0，即ε﹥0，埚N，当n﹥N，有|bn-an|﹤ε.又an≤an+1≤bn+1≤bn，从而正整数p，|an+p-an|≤|bn-an|﹤ε，所以{an}是柯西列，从而收敛，设{an}的极限为r.最后证r=s u p A。n，an不是A的上界，所以a∈A，使an﹤a.由{an}的极限为r，则ε﹥0，埚N，当n﹥N，有r-ε﹤an﹤a﹤r,所以r=s u p A

6 利用致密性定理证明其他实数基本定理

6.1 利用致密性定理证明柯西收敛准则

证[11]：必要性：设an→a﹙当n→∞时﹚，则ε﹥0，埚N∈N，当k﹥N时，有|xn-a|﹤，从而当n，m﹥N时，有

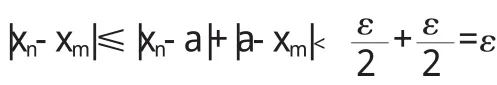
充分性：首先证明满足条件的任何数列必有界.从所设条件，取ε=1，必有一正整数N0，当n，m﹥N0时，有|xn-xm|﹤1

特别地，n﹥N0且m=N0+1时，有|xn-xn0+1|﹤1

所以当n﹥N0时，有|xn|≤|xn-xn0+1|+|xn0+1|≤1+|xn0+1|

这就证明了{xn}的有界性.由致密性定理，必有收敛子列{xnk}，xnk→a﹙当k→∞时﹚，根据子列收敛定义，ε﹥0，必有一正整数K，k﹥K时，有|xnk-a|﹤ε

取一正整数k0=m a x﹙K+1，N+1﹚.于是k0﹥K，且nk0≥nk+1≥N+1﹥N.因此，当n﹥N时，由已知条件知|xn-xnk0|﹤ε，所以|xn-a|≤|xn-xnk0|+|xnk0-a|﹤ε+ε=2 ε

xn→a﹙当n→∞时﹚

6.2 利用致密性定理证明单调有界原理

证[11]：设{xn}是单调上升有上界的实数列.因为{xn}有界，由致密性定理可得，埚{xn}的子数列{xnk}且收敛于r,即ε﹥0，埚K，当k﹥K时，有|xn-r|﹤ε，即r-ε﹤xn﹤r+ε,埚N=nk+1,n﹥N，有xn≥xnk+1﹥r-ε.因为nk→∞，n﹥N，埚nk﹥n，从而xn﹤xnk﹤r+ε，即|xn-r|﹤ε，所以ε﹥0，埚N=nk+1,当n﹥nk+1，有|xn-r|﹤ε，所以{xn}的极限是r.

证[8]：设E=[a,b],｛Oλ｜λ∈Λ｝为一开区间族且(x0)﹥0知，当k充分大时p(xnk)﹤p(x0)和|xnk-x0|﹤p(x0)同时成立，由p(x)定义知，埚λ∈Λ使﹙x0-p(x0)，x0+p(x0)﹚奂Oλ，由|xnk-x0|﹤p(x0)有：﹙xnk-p(x0)，xnk+p(x0)﹚奂﹙x0-p(x0)，x0+p(x0)﹚，所以p(xnk)≥p(x0)，这与p(xnk)﹤p(x0)矛盾，即x∈[a,b]，埚λ∈Λ使﹙x-c，x+c﹚x∈[a,b]的区间中仅用有限个即可覆盖[a,b]，从而｛Oλ|λ∈Λ｝中仅用有限个即可覆盖.

6.4 利用致密性定理证明确界原理

证:A非空有上界则埚a∈A，b∈R使得A∩[a,b]≠覬.将 [a,b]等分为两个闭区间含有A中的点，则将其记为[a1,b1]，否则记埭为[a1,b1].再将[a1,b1]等分为两个闭区间埭，同样偏右选取含有A中的点的子区间为[a2,b2]，如此继续下去，便得到一闭区间套{[an,bn]}，且每个[an,bn]含有A中的点，但右边没有A中的点.由{bn}有界，根据致密性定理得存在{bn}的子数列{bnk}收敛，记，则β即为A的上确界.事实上，x∈A，由bn≥x.k∈Z+圯x≤β.l i mk→∞(bnk-ank)=0（区间套定义）及充分大的k0∈Z+，使得ank0﹥β-ε，[ank0,bnk0]中含有A中的点记为x0圯埚x0∈A，使得x0﹥β-ε依定义，β为A的上确界.同理可

证A非空有下界的情形.

6.5 利用致密性定理证明区间套定理

证:由{[an,bn]}是一闭区间套圯n∈Z+，有a1≤…≤an≤an+1≤bn+1≤bn≤…≤b1圯递增数列{an}与递减数列{bn}都有界，根据致密性定理，存在{bn}的子数列{bnk}收敛，记由{ [an.bn]}是一闭区间套圯由{ank}及{bnk}的单调性圯k∈Z+,a∈[ank,bnk].又n∈Z+,埚k∈Z+，使得[ank, bnk]奂[an,bn]圯n∈Z+，有a∈[an,bn].下证a的唯一性.设n∈ Z+，β∈[an,bn]圯n∈Z+，有0≤|α-β|≤(bn-an)a=β.

〔1〕裴礼文.数学分析中的典型问题与方法.教育出版社,1993：76，78，79.

〔2〕许绍搏，姜东平.数学分析教程.南京大学出版社，1990：75.

〔3〕谢惠民，恽自求，易法槐.数学分析习题课讲义.高等教育出版社,2003：73，76，78,81.

〔4〕袭怀云.数学分析.西安交通大学出版社,2000：29，32.

〔5〕毛雨辉.数学分析选论.科学出版社，2003：17.

〔6〕邓东皋，尹小玲.数学分析简明教程.高等教育出版社, 1999：300.

〔7〕朱正佑，泰成林.数学分析.上海大学出版社，2001：134.

〔8〕孙涛.数学分析经典习题解析.高等教育出版社，2004：91，92.

〔9〕严子谦,尹景学,张然.数学分析.高等教育出版社，2004：17.

〔10〕陈传璋.数学分析.华东师大出版社,1981.

〔11〕陈传璋,金福临,朱学炎.数学分析.高等教育出版社, 1978：104，106.

〔12〕上海交通大学数学系.大学数学分析.高等教育出版社, 2007.

O 17

A

1673-260X（2010）07-0006-06