广东省东莞市第四高级中学(523200) 周应祥

2023 届是新教材新高考第一年,在人工智能、大数据等时代背景下,数学作为基础学科,作为国家选拔人才的重要学科,受到广泛关注,今年高考试题命制质量非常高,命题者的理念先进,契合时代趋势和国家科技发展需要,重点考察考生的数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析等六大核心素养.2023 年高考新课标I 卷第21 题的考点是两点分布、全概率公式和期望线性性质,题目背景是马尔可夫链.

1.高考试题解法赏析与失误原因

题目(2023 年高考新课标I 卷第21 题)甲乙两人投篮,每次由其中一人投篮,规则如下: 若命中则此人继续投篮,若末命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均为0.6,乙每次投篮的命中率均为0.8,由抽签决定第一次投篮的人选,第一次投篮的人是甲,乙的概率各为0.5.

(1)求第2 次投篮的人是乙的概率;

(2)求第i次投篮的人是甲的概率;

(3)已知: 若随机变量Xi服从两点分布,且P(Xi=1)= 1−P(Xi=0) =qi,i= 1,2,···,n.则.记前n次(即从第1 次到第n次投篮)中甲投篮的次数为Y,求E(Y).

1.1 解法赏析

(1)记Ai=“第i次投篮的人是甲”,Bi=“第i次投篮的人是乙”,P(B2)=0.6,过程略.

(2)设P(Ai)=pi,则P(Bi)=1−pi,当n ＞1 时,

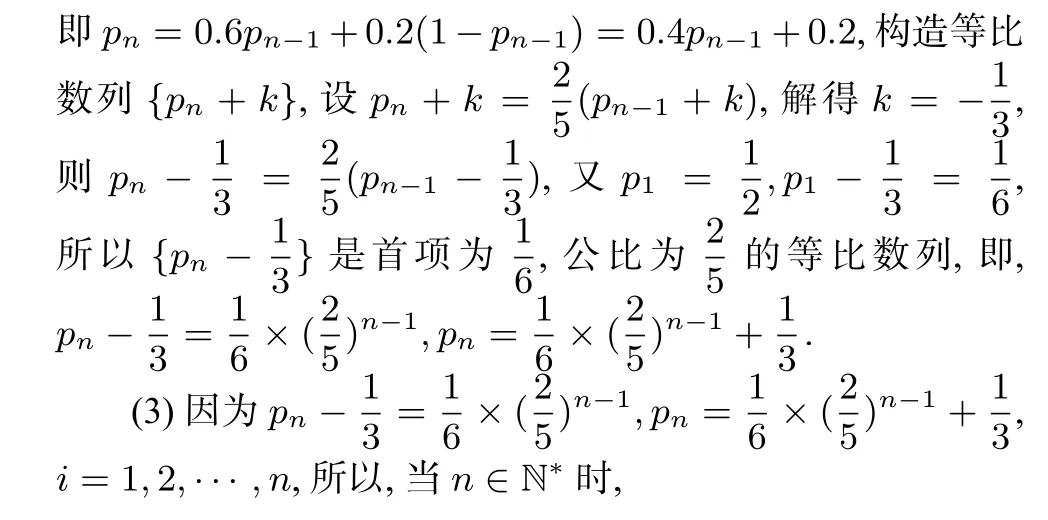
1.2 失误原因

从答卷看,考生解题的典型错误主要有: 没有描述事件或描述不规范,基本概念不清晰,事件与概率概念混淆,将问题情景抽象成数学模型的能力较弱, 对全概率公式不理解,生搬硬套,不会求解一阶线性递推数列通项.第(3)问不会做主要是读不懂题目,数学抽象、逻辑推理、直观想象能力较差.命题者已降低难度,直接告知考生随机变量的期望线性性质,考生需要把每次由谁投篮对应到两点分布,得到甲投篮的次数Y和成功次数相等,即设事件A=“投篮的人是甲”,定义

所以,前n次中甲投篮的次数为Y=X1+X2+···+Xn,,问题就转化为数列分组求和与公式法求和而迎刃而解了!

2.教材背景与拓展研究

该高考试题源自教材[1]第91 页复习参考题7 第10 题.

教材习题 甲、乙、丙三人相互做传球训练,第一次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人.求n次传球后球在甲手中的概率.

解 设Ai=“n次传球后球在甲手中”,P(Ai) =Pi,P1=0,

下面把人数变为进行拓展探究,有什么结论?

拓展探究2 甲,乙,丙,···,N人相互做传球训练,第一次由甲将球传出,每次传球时,传球者都等可能地将球传给另外N −1 中的任何一人.求n次传球后球在甲手中的概率.

解 设Ai=“n次传球后球在甲手中”,P(Ai)=Pi,i=1,2,···,n,P1=0,

结论2 甲, 乙, 丙,···,N人相互做传球训练, 第一次由甲将球传出,每次传球时,传球者都等可能地将球传给另外N −1 中的任何一人.则n次传球后球在甲手中的概率

期望线性性质源自教材[1]第64 页探究.

如果X是一个离散型随机变量,X加一个常数或乘一个常数后,其均值会怎样变化? 即E(X+b)和E(aX)(其中a,b为常数)分别与E(X)有怎样的关系?

探究得出E(aX+b) =aE(X) +b.由E(2X) =E(X+X)=E(X)+E(X)想到:

拓展探究3 如果X,Y均是离散型随机变量,X+Y的均值与E(X)和E(Y)(其中a,b为常数)有怎样的关系?

由E(aX+b) =aE(X)+b容易猜想:E(X+Y) =E(X)+E(Y).

结论3 若随机变量X,Y满足P(Xi) =pi,i=1,2,···,m,P(Yj) =qj,j= 1,2,···,n, 则E(X+Y) =E(X)+E(Y).

证明 设P(X=xi) =pi,i= 1,2,···,m,P(Y=yi)=qj,j= 1,2,···,n, 记P(X=xi|Y=yj) =rij, 则

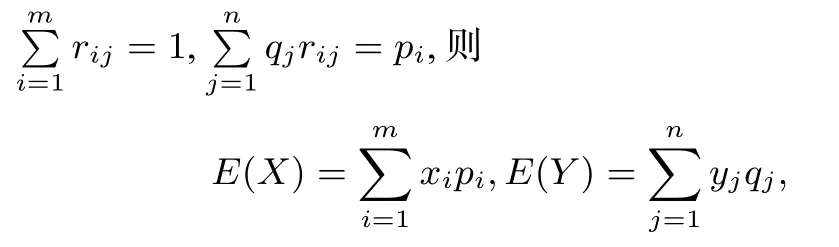
所以,

由结论3 容易得到结论4 和结论5.

结论4 若随机变量Xi服从两点分布,E(Xi) =pi,i=1,2,···,n,则

结论5 对于任意常数ci,i=1,2,···,n及b,有

该高考试题来自教材,突出教材的基础作用.教材是高考试题的来源,是教学中最有效资源.师生回归教材,其需要认真钻研教材,对例题、习题进行深加工,对知识体系进行重新构建、系统整合,理解概念和原理,推导定理、公式,强调知识点纵横联系、数学建模和归类分析,达到高考命题的广度、深度和难度,实现高效学习与备考,提高数学核心素养.

3.加强高等数学背景下的问题研究,增加问题开放性、探究性与趣味性

该高考试题和教材习题的高等数学背景是马尔可夫链.

马尔可夫链定义 状态空间中经过从一个状态到另一个状态的转换的随机过程.该过程要求具备“无记忆”的性质:下一状态的概率分布只能由当前状态决定, 在时间序列中,它前面的事件均与之无关.如果用精确的数学定义来描述,则假设我们的序列状态是

我们在时刻Xt+1的状态的条件概率仅依赖于时刻Xt,即

复杂马尔可夫链问题需要用到二阶(高阶)递推数列求通项方法,例如,

模拟试题 为迅速抢占市场举行促销活动,销售公司现面向客户推出“玩游戏,赢大奖,送汽车模型”活动,客户可根据抛掷骰子向上的点数,遥控汽车模型在方格图上行进,若汽车模型最终停在“幸运之神”方格,则可获得购车优惠券2万元,若最终停在“赠送汽车模型”方格,则可获得汽车模型1 个, 方格图上标有第0 格、第1 格、第2 格,……, 第20 格.汽车模型开始在第0 格,客户每掷一次骰子,汽车模型向前移动一次.若掷出1,2,3,4 点,汽车模型向前移动一格,若掷出5,6 点,汽车模型向前移动两格,直到移到第19 格(幸运之神)或第20 格(赠送汽车模型)时,游戏结束.设汽车模型移动到第n(1 ≤n≤19)格的概率为Pn.

(1)求Pn;

(2)若有6 人玩该游戏,每人一局,求这6 人获得优惠券总金额的期望(精确到万元).

用二阶递推数列求通项方法,可以求出Pn.

(2)设这6 人获得购车优惠券2 万元的人数为X,这6 人获得优惠券总金额为Y,则Y= 2X,X∽B(6,P19),所以,

拓展探究4 记向前移动一格、两格的概率分别为a,1−a,其余条件不变,求Pn.

解Pn=aPn−1+bPn−2,n ＞1,设

结论6 记向前移动一格、两格的概率分别为a,1−a,其余条件不变,

4.应用举例

最后,我们再用拓展探究后得到的6 个结论去解相关的模拟试题.

1.甲、乙、丙、丁4 人在某次传接球训练中,球从甲脚下开始,等可能地随机传向另外3 人中的1 人,接球者接到球后再等可能地随机传向另外3 人中的1 人,如此不停的传下去,假设传出去的球都能接住,记第n次传球之前在甲脚下的概率为Pn,易知P1=1,P2=0.

(1)证明:是等比数列;

(2) 设第n次传球之前球在乙脚下的概率为Qn, 比较Qn与Pn(n≥2)的大小.

2.某学校开展投篮活动,活动规则是: 每名选手投篮n次(n≥3,n ∈N∗),每次投篮,若投进,则下一次站在三分线处投篮;若没有投进,则下一次站在两分线处投篮.规定每名选手第一次站在两分线处投篮.站在两分线处投进得2 分,否则得0 分;站在三分线处投篮,投进得3 分,否则得0 分.已知小明站在两分线处投篮投进的概率为0.7,站在三分线处投篮投进的概率为0.5,且每次投篮相互独立.

(1)记小明前2 次投篮累计得分为X,求X的分布列和数学期望;

(2)记第k次投篮时,小明站在三分线处投篮的概率为ak,k=1,2,···,n,求ak的表达式;

(3)记前n次(即从第1 次到第n次投篮)中小明在三分线处投篮的次数为Y,求E(Y).

3.(2023 年佛山二模)有n个编号为1,2,···,n的盒子,第1 个盒子中有2 个白球1 个黑球,其余盒子中均为1 个白球1 个黑球,现从第1 个盒子任取一球放入第2 个盒子,再从第2 个盒子中任取一球放入第3 个盒子,以此类推,则从第2个盒子中取到白球的概率为____,从第n个盒子中取到白球的概率是____.

4.(2023 年杭州二模) 假如一名赌徒进入赌场参与一个赌博游戏, 每一局赌徒赌赢的概率为50%, 且每局赌赢可以赢得一1 元,每一局赌输的概率为50%,且赌输的就要输掉1 元.赌徒会一直玩下去, 直到遇到如下两种情况才会结束赌博游戏: 一种是手中赌金为0 元, 即赌徒输光; 一种是赌金达到预期的B元, 赌徒停止赌博.记赌徒本金为A(A ∈N∗,A ＜B),赌博过程如数轴示:

当赌徒手中为n(0 ≤n≤B,B ∈N)元时,最终输光的概率为P(n).

(1)请直接写出P(0)与P(B)的数值;

(2)证明:{P(n)}是一个等差数列,并写出公差d;

(3) 当A= 100 时, 分别计算B= 200,B= 1000 时,P(A)的数值,并结合实际,解释当B →+∞时,P(A)的统计含义.

马尔可夫链是2023 届备考的热点问题,在高考中也大放异彩,其热度终将下降,透过现象看本质,找到数学备考内在规律是2024 届高三师生共同任务.笔者认为要充分利用高考试题、教材的习题或模拟试题,建立数学模型,夯实数学基础, 提升数学核心素养, 形成全面的知识体系, 摒弃刷题,反对题海战术,重视知识整合、迁移、系统化,增加问题开放性与探究性,以学生为本,引导学生善于学习,形成数学解决问题的意识,学生复习才会事半功倍!