陈俞怡

【摘  要】  几何中存在大量的性质定理，直角三角形斜边中线性质定理是其中较为常用的一种.问题解析需要提取或构造直角三角形，提取斜边中线或中点，再结合定理推导线段长关系.本文结合实例探究直角三角形斜边中线性质定理的三大常见应用.

【关键词】  直角三角形；斜邊；中线

直角三角形斜边中线性质在求解几何问题中有着广泛的应用.性质定理成立的核心有两点：一是直角三角形；二是斜边上的中线.应用探究有两种思路：一是直接使用性质定理推导线段关系；二是逆向使用证明三角形为直角三角形.下面进行应用探究.

1  推导解析周长

使用直角三角形斜边中线性质定理可以推导求解几何周长问题，求解时提取其中的直角三角形模型，确定斜边以及中线，再结合定理进行线段关系推导.后续构建周长模型，代入线段长完成求解.

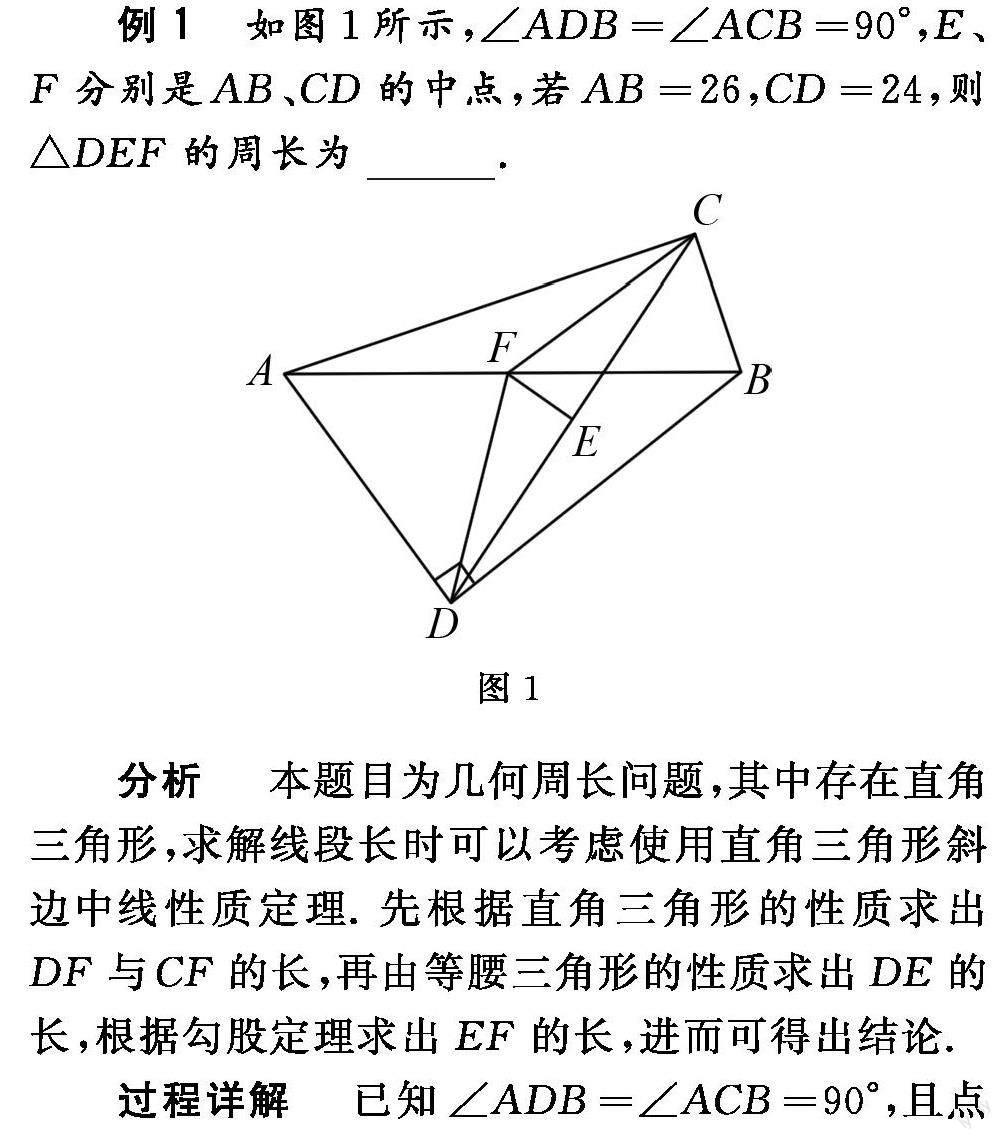
例1  如图1所示，∠ADB＝∠ACB＝90°，E、F分别是AB、CD的中点，若AB＝26，CD＝24，则△DEF的周长为          .

分析  本题目为几何周长问题，其中存在直角三角形，求解线段长时可以考虑使用直角三角形斜边中线性质定理.先根据直角三角形的性质求出DF与CF的长，再由等腰三角形的性质求出DE的长，根据勾股定理求出EF的长，进而可得出结论.

过程详解  已知ADB=∠ACB=90°，且点F是AB的中点，AB=26，

利用直角三角形的斜边中线性质可得DF=CF=，从而可推知△CDF是等腰三角形.

又知点E是CD的中点，CD＝24，

所以EF⊥CD，DE=，

在Rt△DEF中，利用勾股定理可得DE==5.

从而可知△DEF的周长为：DF+DE+EF＝13+12+5＝30.

评析  上述求解三角形周长问题时，应用了直角三角形斜边中线的性质定理，根据定理推导求解DF长，并推导△CDF的特殊性质.对于与几何周长相关的问题，解析时需要注意两点：一是结合周长公式转化为线段和问题；二是注意提取问题中的几何模型，利用模型特性推导线段关系.

2  分析计算角度

直角三角形斜边中线性质定理也可用于几何角度问题推导中，通过分为两步：第一步，提取直角三角形模型，利用斜边中线性质定理推导线段关系；第二步，借助线段关系反推三角形特性，利用三角形特性来推出角度.

例2  如图2所示，已知△ABC中，∠ACB＝90°，O为AB的中点，点E在BC上，且CE＝AC，∠BAE＝15°，求∠COE的度数.

分析  本题目求解几何角度，图中以直角三角形为背景构建了复合图形，问题求解可以利用直角三角形的相关性.

由等腰直角三角形的性质得到∠CAE=∠AEC=45°，求得∠CAB=60°，得到∠B=30°.根据直角三角形的性质得到CO=BO=AO=，得到△AOC是等边三角形，∠OCB=∠B=30°，于是得到结论.

过程详解  已知∠ACB=90°，CE=AC，

则∠CAE＝∠AEC＝45°.

又知∠BAE＝15°，则∠CAB＝60°，所以∠B=30°.

因为∠ACB＝90°，O为AB的中点，

由直角三角形斜边中线性质可得CO＝BO＝AO=，

则△AOC是等边三角形，∠OCB＝∠B=30°，

所以AC＝OC＝CE，

从而可求得∠COE＝∠CEO=（180°﹣30°）＝75°.

评析  上述求解几何角时使用了众多几何性质定理，包括直角三角形斜边上的中线，等腰三角形的性质，等边三角形的判定和性质.解题的关键有两点：一是正确识别图形，提取其中的模型；二是合理利用条件反推几何特性.

3  综合应用解析

直角三角形斜边中线性质定理也可用于综合性问题求解，使用时常与其他几何性质定理相结合，如三角形中位线或中线定理、垂直平分线性质定理等.具体使用同样需分两步：第一步，读题解图，提取几何模型；第二步，利用模型性质定理进行推理分析.

例3  如图3所示，在四边形ABCD中，已知∠ABC＝90°，AC＝AD.点M，N分别为AC，CD的中点，连接BM，MN，BN，回答下列问题.

（1）求证：BM＝MN；

（2）若∠BAD＝60°，AC平分∠BAD，AC＝2，写出求BN长的思路．

分析  本题目为几何综合题，问题解析需要关注其中的直角三角形模型，综合使用性质定理来推导.

（1）根据直角三角形的性质得BM=，由三角形中位线定理得得MN=，根据题意证明.

（2）证明△NMB是等腰直角三角形，根据勾股定理计算即可.

过程详解  （1）证明：已知∠ABC=90°，M为AC中点，

则BM=.

点M为AC中点，N为DC中点，

则MN=.

又知AD＝AC，所以BM＝MN.

（2）已知∠BAD＝60°，AC平分∠BAD，

（3）则∠DAC＝∠CAB＝30°，

（4）所以BM＝AM==1，可推知∠MAB＝∠MBA＝30°，从而有∠CMB＝60°.

根据三角形中位线定理得，MN∥AD，MN=＝1，

所以∠DAC=∠NMC=30°，可知△NMB是等腰直角三角形，

由勾股定理得，BN=.

评析  上述为几何综合问题，两问涉及了证明线段关系，以及求解线段长.具体求解时综合运用了直角三角形的性质定理、三角形中位线定理.利用性质定理推导线段长，分析角度关系，确定三角形特性.对于几何综合题，解析时要注意两点：一是注意拆解图形，提取其中的关键性质；二是定理使用时注意成立条件.

4  结语

总之，直角三角形斜边中线性质定理使用时，需注意提取或构建直角三角形模型，把握问题中的中点、线段等量关系，合理利用性质定理转化推导关系，确定图形特性.探究学习中，需要关注性质定理成立的条件，总结解题思路及构建策略，开展类型题分类探究，总结方法.