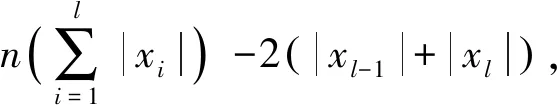马芳玲,原 军

(太原科技大学 应用科学学院,太原 030024)

1 介绍

本文用具有顶点集V(G)和边集E(G)的无向简单图G来表示互连网络。对于简单图而言,定义为没有环,且其中任意两条连杆没有同时连接在相同的一对顶点。完全图定义为任意一对不同的顶点它们之间总会有一条边连接的简单图。从同构的角度分析,由n个顶点组成的完全图,有且只有一个,记作Kn.完全图K5如图1(a)所示。由顶点集X1,X2,…,Xl组成的简单图定义为完全l部图,图中的所有的顶点,均与在不同子集中的其他顶点相互连接;若|X1|=x1,|X2|=x2,…,|Xl|=xl,则这样的图记为T(x1,x2,…,xl).图1(b)是完全二部图T(3,3).

图1 完全图Fig.1 A complete graph

对于两个顶点u,v∈V(G), 如果u和v是彼此相邻的,那么存在一条边e,使得e=uv.对于任意顶点v,它的度dG(v)是与v本身相关联的边数。一个图G,如果对于任何顶点v,都有dG(v)=k,则这个图为k正则的。对于图G中任意顶点v,邻集NG(v)被视作为v的邻点的集合。如果邻集和度的记号未出现符号混淆,则可以省略其下标。V中的一个子集S,在G中如果满足任意两个顶点都不相邻,那么称S是G中的一个独立集。G中的一个独立集S被称为G中的最大独立集,则满足不再存在独立集S′,使得|S′|>|S|成立。这里没有定义的图的术语和符号将遵循文献[1].

设V(G)中任一子集V′,用G-V′来表示,从G中删去V′的全部顶点所得到的图。在连通图G中,使得G-V′不连通的顶点集V′,为图G的一个顶点割。 其中含k个元素的顶点割,被称为k顶点割。完全图是没有顶点割的;在有一对以上相异的且不相邻顶点的G中,G的连通度为k顶点割中最小的k,记作к(G);若G的连通度不为最小的k值,则к(G)定义为|V(G)|-1.

连通度是度量互连网络的可靠性的一个重要参数指标。通常,互连网络的可靠性程度可以用它所对应的图的连通性来衡量。但是,用连通度衡量互连网络的可靠性某种程度上是存在缺陷的[2],因为连通度假设图的任何子集中的所有元素都可能同时失效。鉴于此,Harary在文献[3]中通过提出条件连通度的概念,对这些缺陷进行了弥补。为了让他们拥有预先得到的性质,Harary的条件连通度的理念是限制G-V′的分支。基于这一思想,研究人员对经典的连通度进行了推广,提出了超连通度。

超连通度的定义是Francis T.Boesch[4]和A.-H.Esfahanian[5]提出的。如果顶点割S被称为超顶点割,当且仅当G-S断开连接且没有孤立顶点。这个定义意味着对于任意u∈V(G-S),有NG(u)⊄S.超连通度κ′是所有超顶点割的最小基数,如果有的话,κ′(G)=min{|S|):S⊆V(G)是G的超顶点割}.Fébrega和Fiol在文献[6]中对具有大围长图的超连通度进行了深入的剖析。图的超连通度已经被一大批学者所研究与探索,参见文献[7-8].

给定任意两个图G1和G2,G1和G2的Kronecker积G1×G2是具有顶点集V(G1×G2)=V(G1)×V(G2)和边集E(G1×G2)={(u1,v1)(u2,v2):u1u2∈E(G1),v1v2∈E(G2)}的图。图2为一个图G和K2的Kronecker积,其中V(G)={u1,u2,u3,u4,u5},V(K2)={v1,v2}.

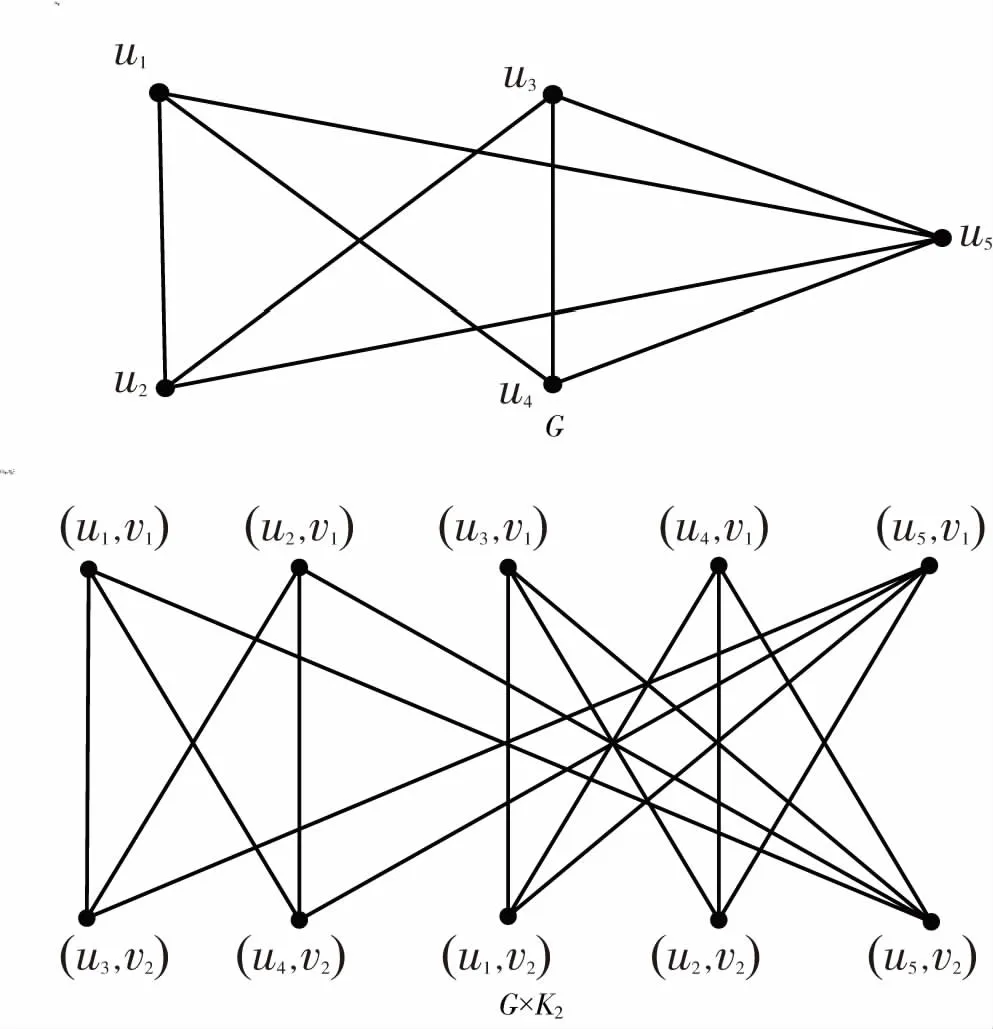
图2 Kronecker积(G×K2)Fig.2 The Kronecker product (G×K2)

图的Kronecker积在图着色、图识别和分解、图嵌入、匹配理论和图的可靠性等方面有着广泛的应用[9-10]。因此,图的Kronecker积得到了很多学者的关注。

在图的Kronecker积的连通度这一研究领域,Miller[11]和Weichsel[12]对两个连通图的Kronecker积的连通度问题开展了研究,对于两个完全图,其Kronecker积的连通度被Mamut和Vumar[13]确定,完全图和二部图的Kronecker积的连通度已由Guji和Weichsel给出[14]。

这些结果在文献[15]中得到了推广。文献[14]还推导出了任意图与阶大于等于3的完全图的Kronecker积的连通度公式。有关图的Kronecker积的更多报告参考文献[16-19].

2 图的Kronecker积的超连通度

在本节讨论了完全图和完全多部图的Kronecker积的超连通度。

对于划分为(X1,X2,…,Xl)的多部图G和完全图Kn(n≥2), 令V1=V(G)={u1,u2,…,um},V2=V(Kn)={v1,v2,…,vn}.对于1≤i≤m,1≤j≤n,令Sj=V1×{vj},X1j=X1×{vj},X2j=X2×{vj},…,Xij=Xi×{vj},…,Xlj=Xl×{vj}.顶点(ui,vj)简写为wij,其中i∈{1,2,…,m},j∈{1,2,…,n}.这意味着对于任意j∈{1,2,…,n},集合Sj=X1j∪X2j∪…∪Xlj={w1j,w2j,…,wij,…,wmj}是G×Kn中的一个独立集,且V(G×Kn)有一个划分V(G×Kn)=S1∪S2∪S3∪…∪Sn.

定理1[12]设G1和G2为连通图。图H=G1×G2是连通的当且仅当G1或G2包含一个奇圈。

引理1[12]设G连通图。如果G没有奇圈,那么G×K2恰好有两个同构于G的连通分支。

完全l部图是顶点集划分为X1,X2,…,Xl的一个简单图,设T(x1,x2,…,xl)是满足|Xi|=xi的完全多部图,Kn为V(Kn)={v1,v2,…,vn}的完全图。

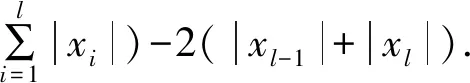
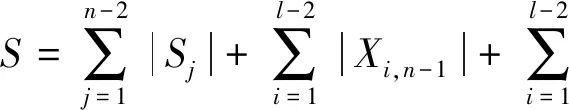
引理3设S是V(T(x1,x2,…,xl)×Kn)的子集,至少三个不同的i值,i∈{1,2,…,n},使得SiS≠∅.如果(T(x1,x2,…,xl)×Kn)-S没有孤立的顶点,则它是连通的。

证明假设存在满足给定条件的S,至少三个不同的i值,i∈{1,2,…,n},使得SiS≠∅.(T(x1,x2,…,xl)×Kn)-S不存在孤立顶点,且是不连通的。

不妨设i∈{1,2,3},S1S≠∅,S2S≠∅,S3S≠∅和一些ji∈{1,2,…,m},存在顶点wjii∈SiS.为了便于表示,将wjii缩写为wi,并考虑关于这三个顶点的以下三种情形。

情形1顶点集{w1,w2,w3}在某Xi×V(Kn)中。

不妨设{w1,w2,w3}⊂X1×V(Kn).由于(T(x1,x2,…,xl)×Kn)-S是不连通的,将进一步划分为两种子情形。

情形1.1 三个顶点{w1,w2,w3}并不都在同一个分支中。这意味着这些顶点中至少有一个顶点与其它两个顶点在不同的分支中。设C是(T(x1,x2,…,xl)×Kn)-S的一个分支且w3∈C,w1∉C,w2∉C.顶点割S必须包含不同分支中顶点的公共邻点。由Kronecker积定义得:

w1∈X1×{v1}=X11,

w2∈X1×{v2}=X12,

w3∈X1×{v3}=X13,

因此,

NT(x1,x2,…,xl)×Kn(w1)∩NT(x1,x2,…,xl)×Kn(w3)=

NT(x1,x2,…,xl)×Kn(w2)∩NT(x1,x2,…,xl)×Kn(w3)=

即:

在这种情况下,NT(x1,x2,…,xl)×Kn(w3)⊆S.因此(T(x1,x2,…,xl)×Kn)-S包含一个孤立顶点w3.这与假设的(T(x1,x2,…,xl)×Kn)-S不存在孤立顶点相矛盾。

情形1.2 三个顶点{w1,w2,w3}在同一分支中,记为C.因为(T(x1,x2,…,xl)×Kn)-S不连通,存在一个顶点w∈(T(x1,x2,…,xl)×Kn)-S,使得w∈V(C′),其中C′≠C.现在,

NT(x1,x2,…,xl)×Kn(w1)∪NT(x1,x2,…,xl)×Kn(w2)∪

因此,w∈X1×V(Kn).w代替w3,变回情形1.1,由情形 1.1推出矛盾。

情形2{w1,w2,w3}中存在两个顶点在某Xi×V(Kn)中,另一个顶点在Xj×V(Kn)中,其中j≠i.不妨设{w1,w2}⊂X1×V(Kn),以及w3∈X2×V(Kn).在这种情况下,因为:

w1=wji1∈X1×{v1}=X11,

w2=wji2∈X1×{v2}=X12,

w3=wji3∈X2×{v3}=X23,

假设:

w1=wj11=(uj1,v1),

w2=wj22=(uj2,v2),

w3=wj33=(uj3,v3),

其中uj1,uj2∈X1,uj3∈X2.所以{w1,w2}⊂NT(x1,x2,…,xl)×Kn(w3),显然它们在同一分支中,记为C.因为(T(x1,x2,…,xl)×Kn)-S不连通,故存在一个顶点w∈(T(x1,x2,…,xl)×Kn)-S,使得w∈V(C′),其中C′≠C.现在,因为

所以:

w∉NT(x1,x2,…,xl)×Kn(w1)∪NT(x1,x2,…,xl)×Kn(w2)∪

这样w∈X13⊂X1×V(Kn).w代替w3,变回情形1.1,由情形1.1推出矛盾。

情形3{w1,w2,w3}中的每个顶点都在不同的Xi×V(Kn).假设{w1}⊂X1×V(Kn),

{w2}⊂X2×V(Kn),{w3}⊂X3×V(Kn).在这种情况下,因为:

w1=wji1=(uji,v1)∈X1×{v1}=X11,

w2=wji2=(uji,v2)∈X2×{v2}=X22,

w3=wji3=(uji,v3)∈X3×{v3}=X33,

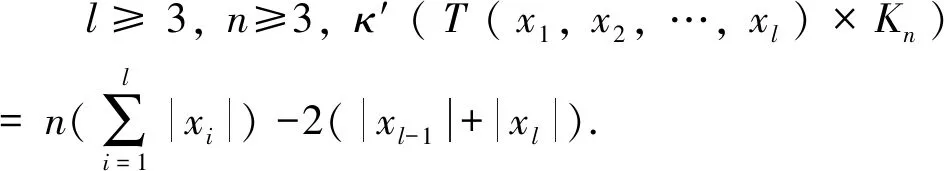
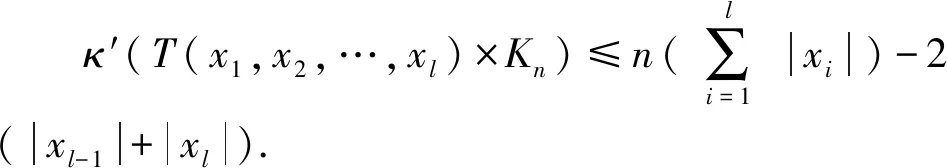
3 结束语