二次函数中动点存在性问题解题策略
——以三角形存在性问题为例
2023-02-15扬州大学数学科学学院圣慧晴
扬州大学数学科学学院 圣慧晴 王 龙
二次函数动点问题中三角形存在性问题是常见的图象动点问题,它是指“通过某一动点把函数具有的基本特征与几何图形加以有效结合”[1],它常将几何运算与函数、分类讨论、方程等问题融合,考查三角形的性质、二次函数的性质等内容.对于该类动点问题,只要认真分析其本质——“变”与“不变”的情况,把握分类依据,对可能的情况进行分类讨论,然后建立相关的函数解析式或方程即可求解.下面将以等腰三角形和相似三角形的存在性问题为例进行说明.
1 例题解析
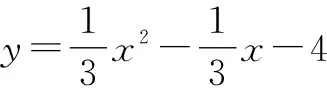
(1)求A,B,C三点的坐标;
(2)试探究在点P运动的过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标;若不存在,请说明理由.

图1
解析:(1)令y=0,可得x1=-3,x2=4 ,故A(-3,0),B(4,0).令x=0,可得y=-4,故C(0,-4).
因此A(-3,0),B(4,0),C(0,-4).
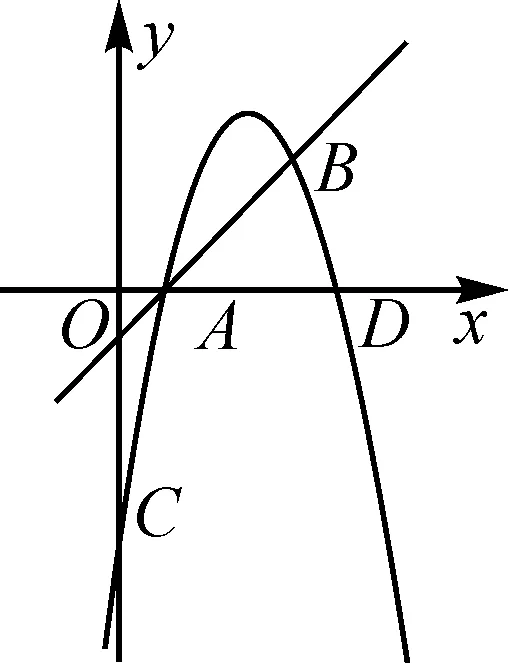
(2)因为B(4,0),C(0,-4),所以lBC:y=x-4.又Q在BC上,可设Q(m,m-4)(0 以A,C,Q为顶点的三角形是等腰三角形共有三种情况,下面分类讨论. 评析:本题考查了二次函数动点问题中等腰三角形的存在问题.第(1)问属于常规问题,较为简单.第(2)问主要考查了等腰三角形的性质以及分类讨论思想,难度属于中等档次.第(2)问究其本质,考查的是等腰三角形两条腰相等的性质,找到这两条腰就是突破本题的关键.题目并没有明确给出哪条边是腰,因此需要进行分类讨论. 图2 例2如图2,在平面直角坐标系中,直线y=x-1与抛物线y=-x2+bx+c交于A,B两点,其中A(m,0),B(4,n),该抛物线与y轴交于点C,与x轴交于另一点D. (1)求m,n的值及该抛物线的解析式; 图3 (2)如图3,连接BD,CD,在线段CD上是否存在点Q,使得以A,D,Q为顶点的三角形与ABD相似?若存在,请直接写出点Q的坐标;若不存在,请说明理由. 故A(1,0),B(4,3). 又点A,B均在抛物线上,则 所以y=-x2+6x-5. (2)存在. 令x=0,得y=-5,故C(0,-5). 因为A(1,0),B(4,3),C(0,-5),D(5,0),所以 因为kAB=kCD,所以AB∥CD. 故∠BAD=∠ADC. 因此,当△ABD与△AQD相似时,只有以下两种情况:①△ABD∽△DAQ,②△ABD∽△DQA.因为点Q在线段CD上,又kCD=1,故lCD:y=x-5,不妨设Q(q,q-5)(0≤q≤5). 图4 图5 评析:本题考查了二次函数的解析式和相似三角形动点存在性问题.第(1)问属于常规问题,比较简单.第(2)问则是在二次函数的基础上融合了三角形相似的内容.求解第(2)问时要关注题目中三角形顶点的顺序问题,再进行分类讨论.对于该题的分类,因为已知有一组角已经相等,即已经确定了一组对应点,那么只需对剩下的两组角相等的情况进行分类,然后联立解方程即可. 从以上两道例题可以看出,在求解二次函数中三角形存在性问题时,常与分类讨论思想相结合.分类的依据是解题的核心与关键,在等腰三角形中,常常以边的相等情况为分类依据;在相似三角形中,角相等或边成比例往往成为分类依据.其次,方程思想也是不容忽视的重要思想,在进行分类后,往往会通过联立方程求解.对于题目中所包含的边、角关系都需要引起重视,这些都可以为联立方程提供依据.最后,三角形存在性问题是建立在二次函数的定义、性质的基础上对问题进行的变式与创新,其本质不变,故能透彻理解和应用二次函数的知识是最基本的要求.对于等腰三角形和相似三角形存在性问题,总结如下解题策略. 证明等腰三角形存在时:(1)写出等腰三角形存在的三种方程;(2)利用坐标之间的关系表示出三条边;(3)将所表示边代入方程求解.值得注意的是,审题需要注意自变量的取值范围,这往往也是限制方程解的条件. 证明相似三角形存在问题:(1)根据题目信息,找出已知可能相等的角或边的比例关系;(2)将剩下的角或边分别进行配对得到相似;(3)根据相似得到边的比例关系,再将各边表示出来代入等式方程求解即可. 总之,掌握二次函数中动点存在性问题的相关解题策略对学生解题有着非常大的帮助作用,本文主要以两种特殊的三角形为例进行展示,希望可以为学生熟练掌握解题技巧,以及灵活运用知识提供助力.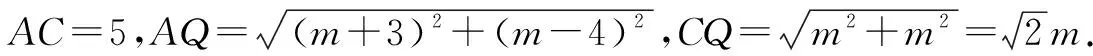



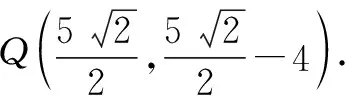

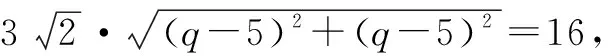

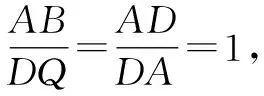


2 策略总结
