徐登明，孟 晨

（中国民航大学a.中欧航空工程师学院；b.理学院，天津 300300）

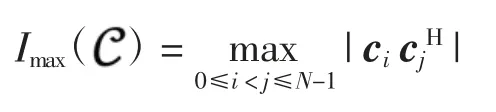
式中cH表示复向量c 的共轭转置。在实际应用中，Imax（）是码本的性能度量，希望码本具有尽可能小的内积互相关值，即对于给定的K，希望构造出N 尽可能大且Imax（）尽可能小的码本。

1974 年，Welch[1]给出Imax（）的一个下界。

引理1（Welch 界） 对任意一个参数为（N，K）且N≥K 的码本都有

此外，等号成立当且仅当对任意的（i，j）且i≠j 都有

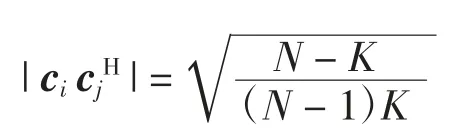
把上述码本的Welch 界记为IW，达到Welch 界的码本称为最优码本，也称为MWBE（maximum-Welch-boundequality）[2]码本。这类码本在CDMA（code division multiple access）通信系统[3]、编码理论[4]等领域都有广泛应用。

然而，最优码本的构造较为困难。多年来，最优码本的构造方法非常有限。在实际应用中，渐近最优码本可以作为最优码本较好的替代品。因此，许多学者致力于构造渐近最优码本，即码本的稍微大于Welch 界，而当N 足够大时几乎达到Welch 界，也即码本的参数满足

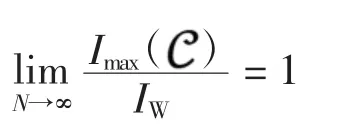
目前构造渐近最优码本的方法有：几乎差集[5-7]、相关差集[8]、二元行选择序列[9-10]、有限域上的指数和[11-13]。最近，在文献[14-15]中，分别利用特征为p2的Galois环R=GR（p2，p2r）和局部环上的指数和给出新的渐近最优码本。由于这些文献所选环的特殊性，导致码本的参数不够灵活，因此，希望在更一般的环上构造出新的渐近最优码本，使其参数更为灵活，这对码本的实际应用是有意义的。

1 预备知识

本小节介绍特征为pn的Galois 环的基本知识，介绍该环上高斯和与Jacobi 和的成果，为之后主要结论的证明做准备。关于Galois 环的更多知识参考文献[16]。

令T={0，1，ξ，ξ2，…，ξq-2}且T*=T -{0}，则任意的元素r∈GR（pn，pns）可以唯一写成r=a0+pa1+p2a2+…+pn-1an-1，a0，a1，…，an-1∈T。此外，r 是可逆元当且仅当a0≠0。设R*表示R 的可逆元集合，M=pR 表示R 的唯一最大理想，则R*=T*×（1+M）。易知|R|=qn，|R*|=qn-qn-1，|M|=qn-1且对每个0≤k≤n有|pkR|=qn-k。

设1≤k≤n，令Rk={a0+pa1+…+pk-1ak-1|a0，a1，…，ak-1∈T}，则每个r∈R*可以唯一写成r=a+pkb，其中a∈R*k，b∈Rn-k。

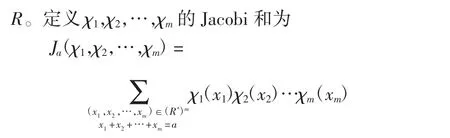
由以下引理可确定平凡情况下Jacobi 和的值，证明方法同文献[12]中的引理4。

引理2设m≥2 且a∈R。方程x1+x2+…+xm=a的解（c1，c2，…，cm）∈（R*）m的数量为

根据文献[18]中的引理3 可得下列结论。

2 渐近最优码本的构造

在本节，给出4 类渐近最优码本的构造。

2.1 第1 类构造

设χ 和λa分别是R 的乘法特征和加法特征。令K=|R*|。定义

2.2 第2 类构造

设χ 和λa分别是R 的乘法特征和加法特征。定义

2.3 第3 类构造

设m≥2，a∈R*。令S（n，m）*={x1+x2+…+xm=a|x1，x2，…，xm∈R*}，K=|S（n，m）*|。取定Rn-1，s的一个乘法特征ψ0。

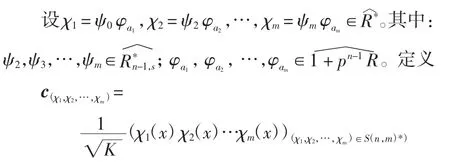
2.4 第4 类构造

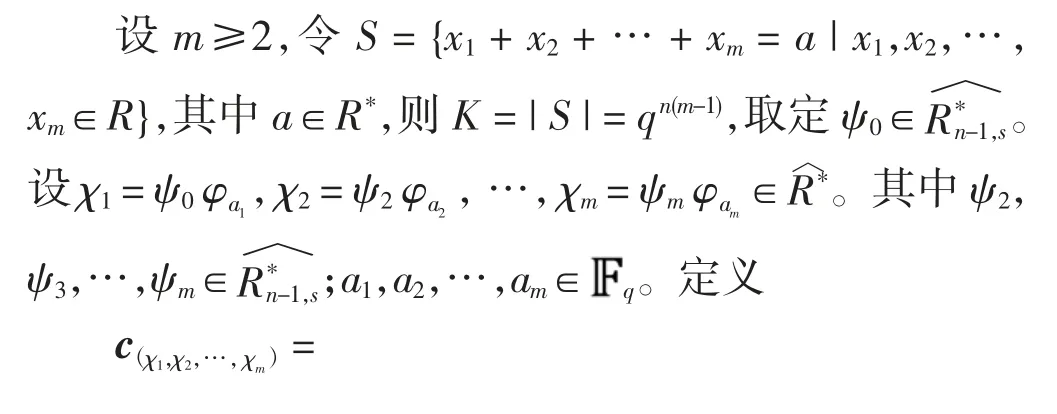
余下的证明同定理3。

3 结语

基于Galois 环上高斯和与Jacobi 和的结论，给出4 类新的码本构造，并证得这些码本关于Welch 界渐近最优。与已有结果进行比较可知，码本参数是新的且灵活的，而且这些码本可以涵盖部分有限域上的相关结论。