立足基础 强化理解 突出变式 提升素养
——由2022年全国乙卷理科第21题引发的思考
2022-11-30安徽
安徽 张 刚
一、问题提出
2022年全国乙卷第21题是在国内疫情持续小范围爆发的社会大环境以及新高考课程和评价体系改革持续推进的背景下命制的试题,试题体现出立足基础知识,重视数学理解,强化灵活运用,考查核心素养,注重平稳过渡的命题原则.本题重点考查函数与导数的综合应用,这类试题可以很好地考查基本函数求导的运算能力,函数与导数之间的转化化归思想,分类讨论思想,较好地实现筛选功能,本文以全国乙卷理科第21题为例,对试题进行深入分析,希望能够给我们的高考复习备考提供帮助.
二、原题呈现
已知函数f(x)=ln(1+x)+axe-x.
(1)当a=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)若f(x)在区间(-1,0),(0,+∞)各恰有一个零点,求a的取值范围.
解析一:(1)当a=1时,f(x)=ln(1+x)+x·e-x,
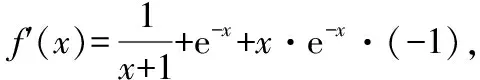
所以f′(0)=1+1=2,
因为f(0)=0,
所以所求切线方程为y-0=2·(x-0),即y=2x.
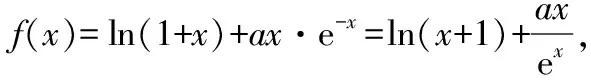
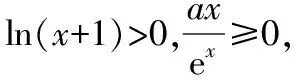
所以f(x)>0,所以f(x)在(0,+∞)上无零点,不符合题意.

令g(x)=ex+a(1-x2),则g′(x)=ex-2ax,
g′(x)在(-1,+∞)上单调递增,g′(-1)=e-1+2a,g′(0)=1,
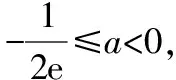
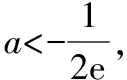
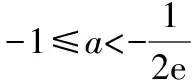
(ⅱ)当g(0)<0,即a<-1时,存在x1,x2使f(x)在(-1,x1),(x2,+∞)上单调递增,在(x1,x2)上单调递减.
因为f(0)=0,所以f(x1)>f(0)=0,
当x→-1时,f(x)<0,所以f(x)在(-1,x1)上存在一个零点,即f(x)在(-1,0)上存在一个零点,
因为f(0)=0,
当x→+∞时,f(x)>0,所以f(x)在(x2,+∞)上存在一个零点,即f(x)在(0,+∞)上存在一个零点.
综上,a的取值范围是(-∞,-1).
点评:本题主要考查曲线在某点处的切线方程、分类讨论思想、零点存在问题等,考查的核心素养是逻辑推理、数学抽象、数学运算.解决此类问题的关键:一是会求基本函数f(x)的导函数,借助在切点处的导函数值即为斜率,利用点斜式即可求出切线方程;二是根据函数f(x)的结构特点,恰当地对参数a进行合理分类,讨论判断该区间有无零点存在,而局部构造合理的新函数,研究单调性是判断零点存在的关键所在,对于隐零点问题,有时可考虑设而不求思想,继续探究新函数的单调性,从而逼出参数的取值范围,这也是难点所在.
三、试题探究
1.知识探源
最近5年(2018年-2022年)全国乙卷(含全国Ⅰ卷)理科函数与导数压轴题的考查方向,列表如下
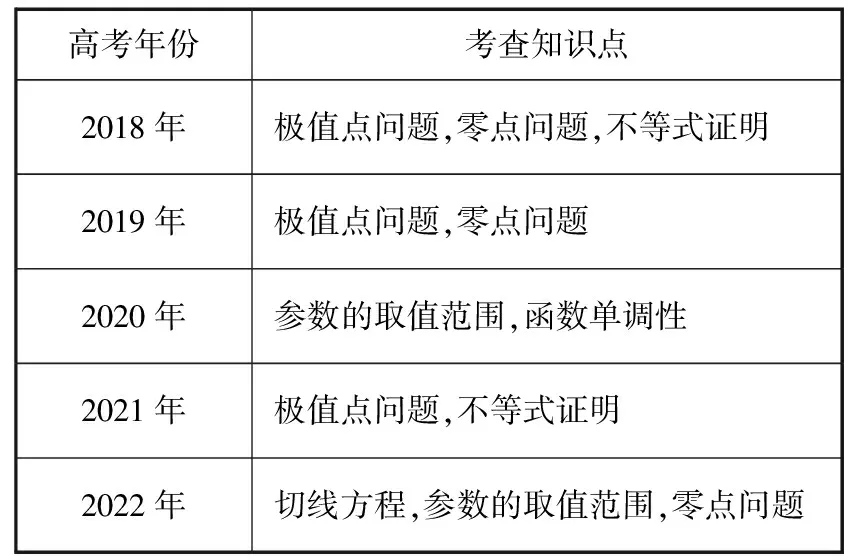
续表
从上表我们可以得出一些结论:(1)从命题变化的方向来看,试题方向更加明确,侧重考查学生“四翼”,更加强化基础知识扎实以及综合性的融会贯通.(2)从考查的重点来看,试题越来越注重导数与不等式的交汇问题.例如,2018年、2019年、2021年均涉及考查极值点问题.2018年、2019年、2022年均涉及考查零点问题.2020年、2022年均涉及考查参数的取值范围问题.(3)从设计的知识点来看,试题越来越综合,强化关键能力的理解与运用,注重考查学生的创新意识与创新思维.例如,2018年到2022年大部分年份试题的第1问都是低起点、重基础,第2问就加大思维考查难度,需要通过转化化归、分类讨论、参变分离、构造新函数等思想与方法相结合,综合处理数学问题.(4)2022年试题计算量较大也是一个很大地挑战,未来高考数学试题将会持续保持这一趋势,这也是国家人才战略发展的必然要求.
3.解法探究
2022年全国乙卷第21题的第1问这里不再展开叙述.下面重点对第2问进行深入分析,普遍性的解法就是对参数进行恰当分类,再构造新函数判断单调性,确定零点存在情况.借助新函数求导转化为导函数在给定区间上的单调性的关键是如何恰当分类,这也是本题的难点所在.
基于以上理解,我们也可以先参变分离,再从二次求导(或数形结合)入手,解决此类问题.笔者经过思考分析,给出如下解法.
解析二:参变分离,二次求导法
令g(x)=exln(x+1)+ax=exf(x)(x>-1),


于是g(x)在(0,+∞)上单调递增,g(x)>g(0)=0与g(x)在(0,+∞)上有一个零点矛盾.
(2)若a<-1,

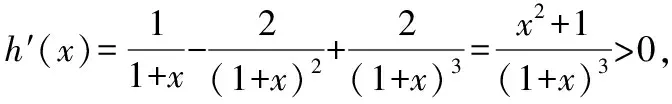
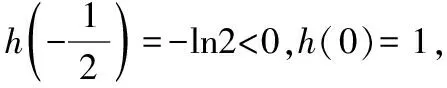
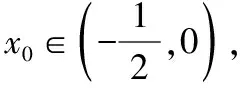
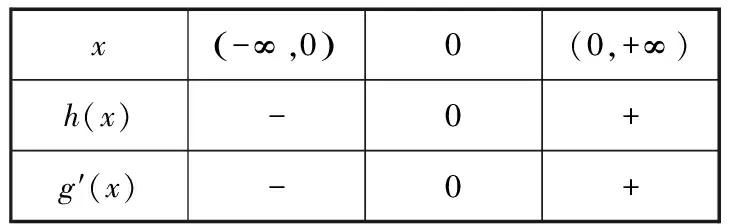
g′(x0) 存在x1∈(-1,x0),x2∈(0,-a),使得g′(x1) 解析三:参变分离,数形结合法 令exf(x)=0⟺-ax=exln(1+x), 令y=-ax,h(x)=exln(1+x), 当-1 从而l(x)在(-1,0)上单调递减,在(0,+∞)上单调递增,而l(0)=1,所以h′(x)>0,从而h(x)在(-1,0)和(0,+∞)上单调递增,而h′(0)=1也就是h(x)在原点处的切线斜率,又y=-ax过原点,可知需-a>0;又知x=-1是h(x)图象的一条渐近线,所以在(-1,0)内h(x)递增时一定是上凸的,又在(0,+∞)内,当x→+∞,h(x)=exln(1+x)>ex,所以此时h(x)是下凹的;要使f(x)在区间(-1,0),(0,+∞)上各恰有一个零点,此时只需-a>1,即a<-1即为所求. 点评:第(2)小问属于函数零点分布中求参数的范围问题.通常把参数a合理分类,然后对原函数求导后,在局部构造新函数二次求导,判断其单调性,根据区间零点存在,确定参数a的取值范围.解法二借助一次求导确定g(x)在(0,+∞)上的单调性,再局部构造h(x)判断其在(-1,+∞)上的单调性,利用虚设零点原理证明存在.而解法三则是通过数形结合思想分别构造函数y=-ax,h(x)=exln(1+x),求导判断导函数的单调性,借助h(x)与y=-ax的位置,确定函数图象的凸凹性,从而根据零点分布区间,求出a的取值范围. 4.1所求问题由“双区间、双零点”型弱化为“单区间、单零点”型 如果我们将2022年全国乙卷理科第21题的第(2)小问题干条件进行弱化变式,降低思维考查的难度,比如,将所求问题由“双区间、双零点”型变为“单区间、单零点”型,虽然所求区间和零点个数减少了,但本质不变,我们仍然可以根据函数f(x)的结构特点,求导后局部合理构造新函数,可继续考虑设而不求思想,探究新函数的单调性,结合零点存在的区间,从而逼出参数的取值范围,只要注意把握好对参数a的分界,问题不难获得求解,这里略举一例说明. 【例1】(2022·福州高中毕业班质量检测)已知函数f(x)=ex-axsinx-bx+c的图象与x轴相切于原点. (1)求b,c的值; (2)若f(x)在(0,π)上有唯一零点,求实数a的取值范围. 解析:(1)b=1,c=-1. (2)由(1)得f′(x)=ex-a(sinx+xcosx)-1, 记g(x)=ex-a(sinx+xcosx)-1, 则g′(x)=ex-a(2cosx-xsinx),所以g′(0)=1-2a. 因为g(0)=0,g(π)=eπ+aπ-1>0,所以g(x0)<0,所以存在唯一实数x1∈(x0,π),使得g(x1)=0,所以当x∈(0,x1)时,g(x)<0,即f′(x)<0,f(x)单调递减. 因为f(0)=0,f(π)=eπ-π-1>0,所以f(x1)<0,所以存在唯一实数x2∈(x1,π),使得f(x2)=0,即f(x)在(0,π)上有唯一零点,符合题意. 点评:第(2)小问属于函数零点分布中求参数范围问题,通常构造新函数研究其单调性,并且合理对参数a的分界.在二次求导的基础上,借助虚设零点原理确定导函数的单调性,最后求出导函数的最小值即可,而如何准确确定参数a的分界点是问题的关键. 4.2所求问题由“双区间、双零点”型变式为“不限区间、单零点”型 如果我们将2022年全国乙卷理科第21题的题干再作一些变式,比如,将所求问题由“双区间、双零点”型变式为“不限区间、单零点”型.虽然表达式的结构更复杂,但本质不变,我们仍可以运用参变分离,二次求导法解决,但是需要注意的是参变分离后,构造的新函数要根据新函数的局部结构,再构造新函数,进而二次求导,这也是突出对学生变式问题的强化理解,学生高阶思维水平的展现.下面也略举一例说明此情况. 【例2】(2022·南京市、盐城市高三二模改编)设函数f(x)=aex+sinx-3x-2,e为自然对数的底数,a∈R.若函数f(x)有唯一的零点,求a的取值范围. 解析:当a≤0时,f′(x)=aex+cosx-3<0,所以f(x)单调递减,又当x→-∞时,f(x)→+∞,当x→+∞时,f(x)→-∞,所以存在唯一的x0∈R,使得f(x0)=0,即函数f(x)有唯一的零点. 设h(x)=cosx-sinx+3x-1,则h′(x)=-sinx-cosx+3>0,所以h(x)单调递增,又h(0)=0,所以可以列表为 x-∞,0()0(0,+∞)h(x)-0+g′(x)-0+ 所以g(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,又x→-∞时,g(x)→+∞,当x→+∞时,g(x)→a,且a>0,所以若g(x)有唯一零点,则g(x)min=g(0)=a-2=0,解得a=2.综上,a的取值范围为(-∞,0]∪{2}. 4.3所求问题由“双区间、双零点”型强化为“不限区间、双零点”型 如果我们将2022年全国乙卷理科第21题的题干再强化一下变式.比如,将所求问题由“双区间、双零点”型变式为“不限区间、双零点”型.虽然所求零点区间不限,但本质不变,我们仍可以运用参变分离,数形结合法解决,但是需要注意的是参变分离后,构造新函数需要考虑函数图象的交点位置,借助零点满足的条件,得出a的取值范围,下面通过实例说明. 【例3】(2020·华南师大附中高三月考改编)设函数g(x)=(x-1)ex+ax2,a∈R. 若函数g(x)有两个零点,试求a的取值范围. 当x>0时,h′(x)<0,函数h(x)单调递减;当x<0时,h′(x)>0,函数h(x)单调递增,故由h(x)的图象可知,若有两个交点,则a的取值范围为(0,+∞). 点评:本题仍是利用先参变分离,构造含参数a的新函数,借助研究新函数h(x)的单调性,通过图象交点位置,确定参数a的范围,数形结合法最直观. 《普通高中数学课程标准(2017版2020年修订)》指出:“数学抽象是指对数量关系与空间形式的抽象,得到数学研究的素养.逻辑推理是指从一些事实和命题出发,依据规则推出其他命题的素养.”数学基础性包括学科内容的基础性、解法的通用性以及创设情境的典型性.它是以学习者在学习探索中最基础的问题情境和基本知识能力的考查为载体,是学生升入高校进一步学习的必备知识与核心能力的体现.这就要求我们在高三复习过程中,遵循知识体系,进行有条理地梳理、归纳,特别是重点知识、易错点、基本的数学思想方法等,经过长期的训练形成习惯,学习力和能力才能同步提高.2022年是全国乙卷向新高考卷的过渡之年,提高自身学力,强化数学知识与方法的深度学习与理解,才能以不变应万变. 例如,本文所述第21题中第(2)小问中区间零点含参取值范围的问题,是在导函数参变分离的基础上,进行的求导运算,这就要求我们首先对基础计算、公式变形求导都要过关,其次,导数概念、法则、零点存在定理以及导函数的单调性要理解本质,明确由于参数a的范围不确定,导致对函数分界点进行讨论,特别是分类如何界定,最后我们更要明理,理解导函数各部分知识的关联点在什么地方,提高运算的准确性和速度,适度掌握一些必要的解题技巧,而不是盲目下手解答,草草收场. 中国高考评价体系中强调高考就是要求学生基础扎实,学会融会贯通.数学是思维性很强的学科,在高考数学复习中,要注重“一题多变”(即变式的延伸、弱化、加强与推广)、“一题多用”(即用同一数学思想方法解决不同问题),更多地关注高考试题的核心是什么,学会从试题中提炼反映数学试题变式本质的东西. 例如,试卷第21题中涉及函数区间零点含参取值范围的问题,就是一类典型问题,需重点复习.比如,所求问题由“双区间、双零点”型弱化为“单区间、单零点”型,再变式为“不限区间、单零点”型,最后强化为“不限区间、双零点”型,都可以运用化归思想,采用分离参数,数形结合方法,实现导函数单调性的确定,最后根据区间零点分布,采用虚设零点,合理确定分类讨论的界点.由于试题本质不变(以参数a与自变量x分离为最终目标),所以通法不变,问题自然也容易类比解决,变式思想就是不断更换命题的非本质特征,保留对象中本质因素,通过不同角度、层次、背景的变化,有意识引导学生从“变”中发现“不变”的本质,寻求“不变”的规律.所以注重解题思维训练和变式能力培养都是十分有必要的. 数学概念、性质、公式、原理都是高考数学中必备知识,也是数学解题的基础与关键,数学运算与推理能力薄弱往往是由于我们在日常中,过度关注解题数量,忽视数学知识前后体系的建立,知识结构出现碎片化,从而造成推理和计算时,含糊不清,以偏概全,乱套公式的现象,这也是目前高考数学答题失分严重的重要原因之一.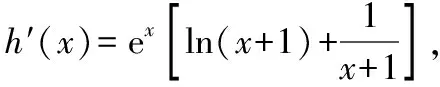
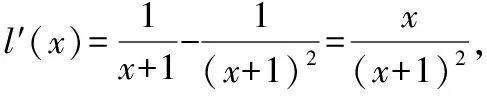
4.变式跟踪及简评
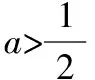


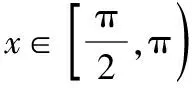

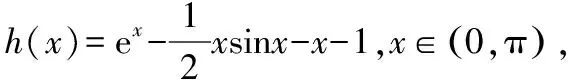


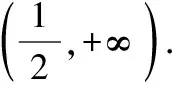
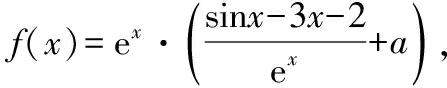
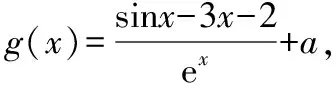

四、教学思考
1.立足学生基础,强化数学理解
2.注重通性通法,突出变式思想
3.完备知识结构,提升数学素养

