◎沈杜宇 刘凯峰

(1.南通大学数学师范211班，江苏 南通 226019；2.南通大学理学院数学系，江苏 南通 226019)

一、构造同构方程

《义务教育数学课程标准(2011年版)》提出，应当注重发展学生的数感，数感主要是指关于数与数量、数量关系、运算结果等方面的感悟.在中学数学学习中“式”也不在少数，类比于“数感”，我们可以提出“式感”.构造函数、构造方程等就反映了解题者对不同变量、不同数学对象之间的关系所具备的平衡感与敏锐度.相对而言，“式感”应该是一种比“数感”更复杂、更微妙的感悟.

同构方程简单地说就是“同样结构的方程”，即若干个元素具有同样的关系式，满足同一个方程.当然，同构方程一般比较隐蔽，需要我们用敏锐的眼光去发现，并将之呈现出来.在高中数学学习中，同构思想经常出现，近年来的高考数学试卷中也频频出现利用同构思想解题的题目.例如，ex≥ln(x+a)+a可以巧妙地变形为ex+x≥eln(x+a)+ln(x+a)，于是我们构造函数F(x)=ex+x，原不等式即F(x)≥F(ln(x+a))，利用函数的性质可推出x≥ln(x+a).本文我们不打算谈大家比较熟悉的同构函数，而主要谈谈同构方程.

二、构造同构方程举例

下面我们举数列、代数、解析几何方面的9个例子，这些例子都是先通过观察发现两个不同的数学对象满足相同的数学关系，然后构造相同的方程，简洁明快地解决问题.解决这一类问题往往比较困难，解题者一拿到手可能没有思路，尤其是一些问题中并没有出现式子，需要解题者在思考过程中敏锐地觉察出题中隐含了一个与其他式子相同结构的式子，得到同构方程.

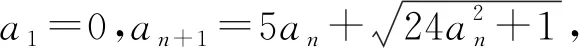
证明因为a1=0,a2=1，所以由题设知当n≥1时an+1>an.

①

当n≥2时，把①式中的n换成n-1得

②

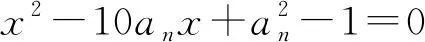
再由a1=0,a2=1及上式可知，当n∈N+时，an都是整数.

例2设am+an=ap+aq,a3m+a3n=a3p+a3q，(a>0,a≠1).

证明：mn=pq.

证明据第一式立方,得a3m+a3n+3am+n(am+an)=a3p+a3q+3ap+q(ap+aq)；

所以有am+n=ap+q，故得m+n=p+q.从而am·an=ap·aq.

若记am+an=ap+aq=b，am·an=ap·aq=c，则am,an是方程x2-bx+c=0的两根，

ap,aq也是此方程的两根，因此，am=ap，an=aq，得m=p,n=q；或者am=aq，an=ap，得m=q,n=p.总之都有mn=pq.

点评容易看出本题与立方和公式有关.已知两数和与两数积，逆用韦达定理构造方程是一种高级技巧.

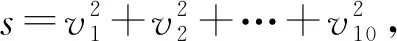
从而，每个vi均为此二次方程的两根之一.对于固定的s，设这两个根为a，b.

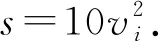
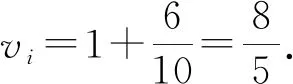
否则，a，b之一至少出现5次.不妨设vi中a出现了5+k(0≤k≤4)次，剩下的vi为b，且出现了5-k次，又所有的vi均不小于1，由均值不等式得

故6ab=9a2+b2⟹(b-3a)2=0⟹b=3a.

将10个方程相加得v1+v2+…+v10=16.

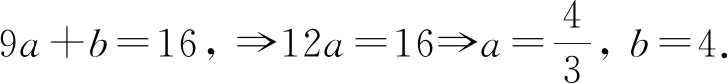
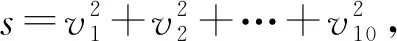
例4(2011年浙江高考)如图1，已知抛物线C1:x2=y，圆C2:x2+(y-4)2=1的圆心为点M.

图1

(1)求点M到抛物线C1的准线的距离.

(2)已知点P是抛物线C1上一点(异于原点)，过点P作圆C2的两条切线，交抛物线C1于A，B两点，若过M，P两点的直线l垂直于AB，求直线l的方程.

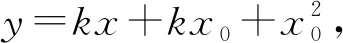
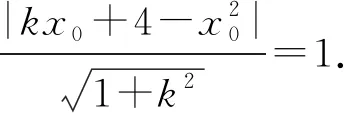
设PA，PB的斜率为k1,k2(k1≠k2)，则k1,k2是上述方程的两根，所以

将①代入y=x2得x2-kx+kx0-x02=0，

由于x0是此方程的根，故x1=k1-x0,x2=k2-x0,

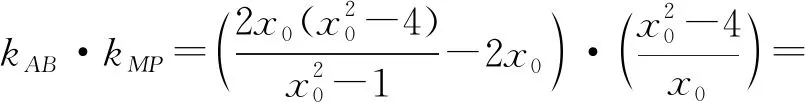
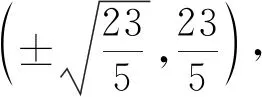
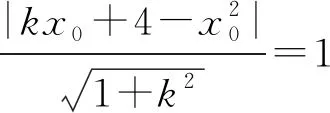
例5已知抛物线y=x2，圆E： (x-2)2+y2=1，抛物线上三点分别为A(a,a2),B(b,b2)和C(c,c2)，这里a≠±1，且AB,AC均与圆E相切.试用a表示b+c,bc.

解析直线AB的方程y-(a+b)x+ab=0.

又圆心(2,0)到AB的距离为1，

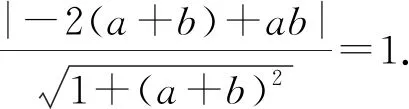
化简得(a2-4a+3)b2+(6a-4a2)b+3a2-1=0.

同理有(a2-4a+3)c2+(6a-4a2)c+3a2-1=0.

即b,c是关于x的一元二次方程(a2-4a+3)x2+(6a-4a2)x+3a2-1=0的两根.

点评从目标式b+c,bc，我们能看出一点韦达定理的影子.

例6已知实数p>0，且过点M(0,-p2)的直线l与曲线C：x2=2py交于A,B两点.

(1)设O为坐标原点，直线OA,OB的斜率分别为k1,k2，若k1·k2=1，求p的值.

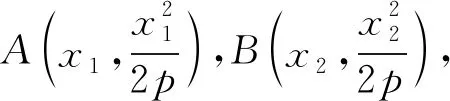
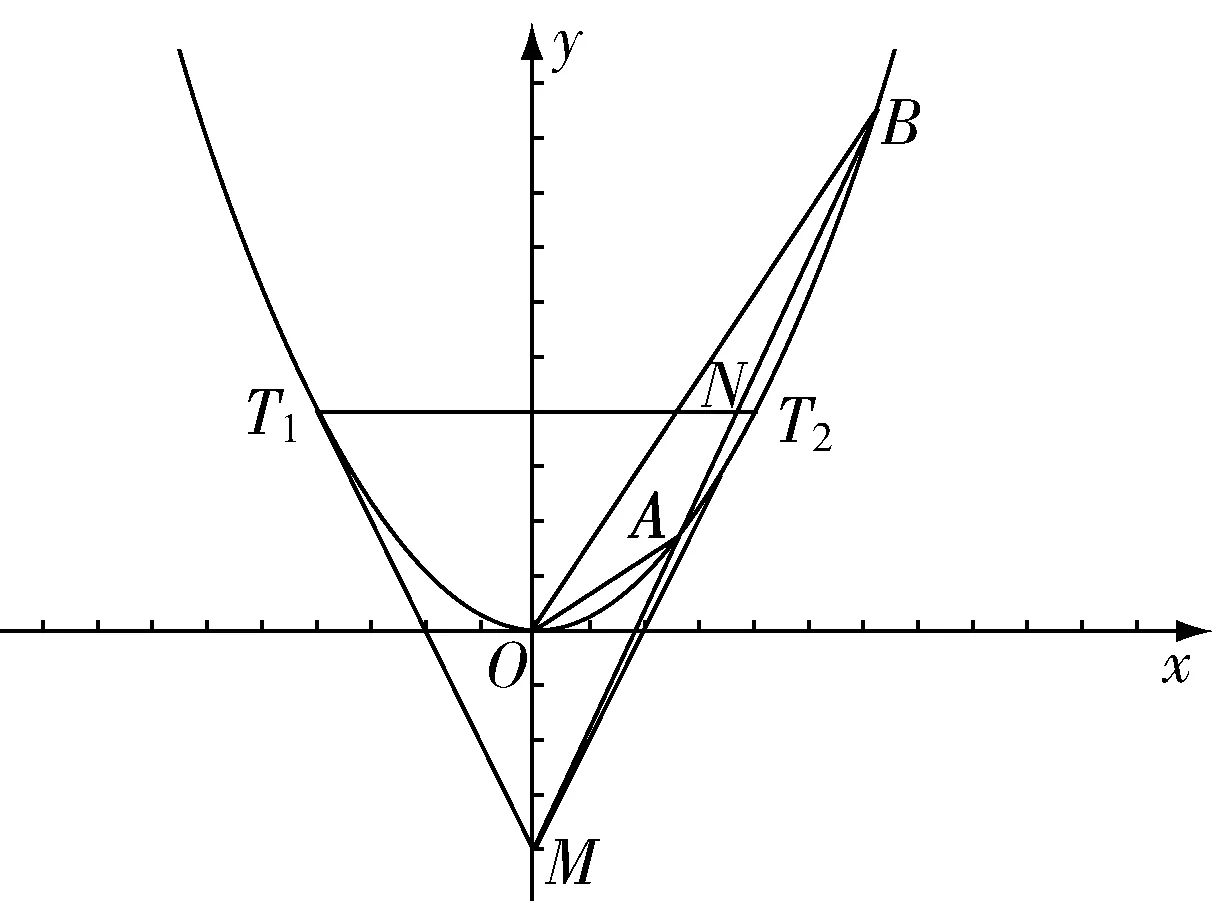
图2

设直线AB方程为y=kx-p2，与x2=2py联立，消去y，得x2-2pkx+2p3=0.

所以x1·x2=2p3=4p2，所以p=2.

(2)证明设点N(x0,y0)，T1(x3,y3)，T2(x4,y4)，

则点T1处的切线方程为x·x3=2(y+y3)，代入点M，得y3=4，同理可得y4=4.所以直线T1T2的方程为y=4，所以y0=4.

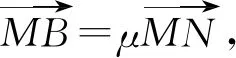
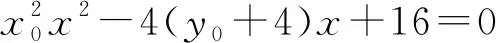
点评两组相关点法，如果蕴含某种对称性，往往就会出现同构方程.

例7已知抛物线x2=4y，直线y=kx+1交抛物线于A,B两点，P是抛物线外一点，连接PA,PB分别交抛物线于点C,D，且CD∥AB.若k=1，求点P的轨迹方程.

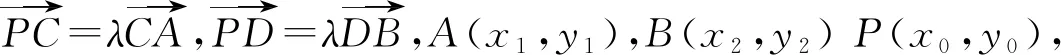
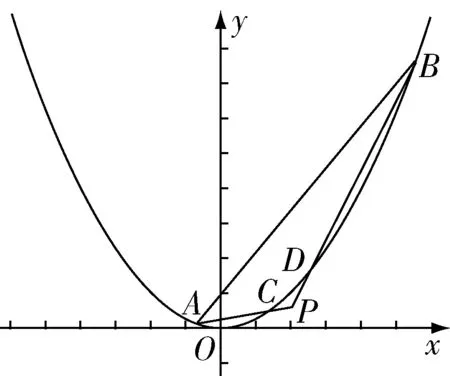
图3

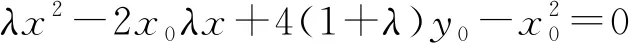
同理可得x2也为方程的根.联立①式得x1+x2=2x0=4k=4，解得x0=2.

所以点P的轨迹方程为x=2(y<1).

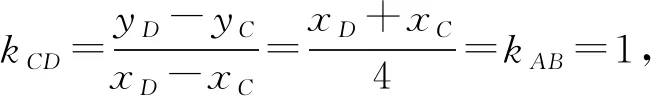
点评解析1利用了向量、定比分点知识来表明平行关系；解析2利用了斜率来表明平行关系.处理好了一个数学对象，若能如法炮制处理另一个数学对象，就有可能构造出一个共同代数式、函数、方程等.当然，构造方程解决问题不一定会更简单，例如本题解析2没有利用同构方程而解答更加简单.

(1)证明：点Q是线段MN的中点.

(2)分别过点M,N作双曲线的切线l1,l2，证明：三条直线l,l1,l2相交于同一点.

(3)设点P为直线l上一动点，过点P作双曲线的切线PA,PB，切点分别为A,B.证明：点Q在直线AB上.

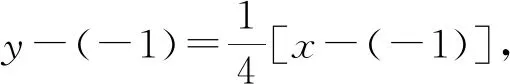
设M(x1,y1),N(x2,y2)，则x1,x2是方程的两根，所以x1+x2=-2，

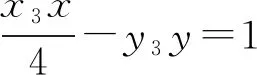
于是，无论x0取什么值(即无论P为直线l上哪一点)，点Q(-1,-1)都在直线AB上.

点评本题是一道2007年全国高中数学联赛浙江省预赛题，题目结论优美，综合性较强，集中体现了构造同构方程解决问题的思想方法.如果解题者不具备构造同构方程求解的经验，解题过程会比较烦琐，甚至困难重重.

三、结束语

构造同构方程需要学生有较高的数学素养，但这不是一朝一夕就能掌握的.在平时的教学中，数学教师可以选取典型题目，采用两种方法进行分析，一种方法不需要构造同构方程，另一种方法则需要构造同构方程，通过对比，让学生体会构造同构方程解题的巧妙之处.在初中数学学习和高中数学学习中，学生都会遇到构造同构方程的问题，尤其是高中阶段学习解析几何的内容时，这样的问题更多些.教师在高中二轮复习数学思想方法微专题教学中，可以开辟类似的专题引导学生总结反思，有利于提高学生的数学素养.