李洋洋 刘会

(1.四川大学附属中学,成都,610044;2.武汉大学数学与统计学院,武汉,430072)

1 Introduction

The study on closed characteristics in the global sense started in 1978,when the existence of at least one closed characteristic was first established on any Σ∈Hst(2n)by Rabinowitz in[32]and on any Σ∈Hcon(2n)by Weinstein in[38]independently. Since then the existence of multiple closed characteristics on Σ∈Hcon(2n) has been deeply studied by many mathematicians, for example, studies in [10, 11,18,20,29,30,31,35,37,39]for convex hypersurfaces. For star shaped hypersurfaces, in[4]and[16],#T(Σ)≥nfor Σ∈Hst(2n) was proved under some pinching conditions. In [36], Viterbo proved a generic existence result for infinitely many closed characteristics on star shaped hypersurfaces. In [17],Hu and Long proved that#T(Σ)≥2 for Σ∈Hst(2n)on which all the closed characteristics and their iterates are non degenerate. In [19], Hofer, Wysocki, and Zehnder proved any non degenerate compact star shaped hypersurface has either two or infinitely closed characteristics, provided that all stable and unstable manifolds of the hyperbolic closed characteristics intersect transversally. In 2016,#T(Σ)≥2 was first proved for every Σ∈Hst(4)by Cristofaro Gardiner and Hutchings in[5]without any pinching or non degeneracy conditions. Different proofs of this result can also be found in[12],[15]and[22]. For the recent progresses on closed characteristics on compact star shaped hypersurfaces,one can also refer to[8,9,13,14,23,24]and the references therein.

It is very interesting to consider closed characteristics on hypersurfaces with special symmetries.Note that there are many studies about closed characteristics on compact convexPcyclic symmetric hypersurfaces,one can refer to[6,7,21,26,27,40]. In this paper,we study the multiplicity ofPcyclic symmetric closed characteristics on compact star shapedPcyclic symmetric hypersurfaces under a pinching condition. Letk ≥2 be a positive integer andP=, where

Theorem 1.1There holds#TP(Σ)≥1 for any Σ∈(2n).

Letn(y)be the unit outward normal vector of Σ atyandd(y):=n(y)·y,i.e.,the distance between the origin of R2nand the tangent hyperplane to Σ aty. Thend(y)> 0 for ally ∈Σ since Σ is strictly star shaped. Letd=min{d(y):y ∈Σ},R=max{|y|:y ∈Σ}andr=min{|y|:y ∈Σ}.

Theorem 1.2AssumeR2< (k+ 1)rdfor some Σ∈(2n). Then there exist at leastngeometrically distinctPcyclic symmetric closed characteristics on Σ.

Remark 1.1LetP=−I2nandk= 2,then Theorems 1.1–1.2 are the main results of[16]. Thus our results are slightly extensions of those of[16]. We should emphasize that we follow the ideas of[16].Compared with[11]and[26],the pinching condition of Theorem 1.2 is slightly broader,and it’s used to guarantee the closed characteristics we obtained are prime and geometrically distinct. The topic aboutPcyclic symmetric closed characteristics on compact star shapedPcyclic symmetric hypersurfaces are interesting, one can also refer to [1], [25]and [28]for the recent studies on convexPcyclic symmetric hypersurfaces. Note that our Theorem 1.2 extends Theorem 1.21 of [1] to the star shaped case. Our Theorem 1.2 also has potential applications to celestial mechanics,for example in[34],the H´enon Heiles Hamiltonian energy level presents Z3symmetry and the Hamiltonian energy level presents Z4symmetry in Hill’s lunar problem.

2 Proof of Theorem 1.2

We shall prove Theorem 1.2. Theorem 1.1 will be an easy consequence.

LetH(x)=j2(x),∀x ∈R2n,wherej:R2n →R is the gauge function of Σ,that is,j(λx)=λforx ∈Σ andλ ≥0. Then Σ=H−1(1)andH(Px)=H(x)since Σ∈(2n). In the following,we will find distinct solutions of the Hamiltonian system

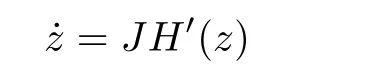
lying on Σ satisfying thatz(t+τ)=Pz(t)for someτ>0.

SetE=(R/(kπ)Z,R2n). Foranysmoothu∈E,we consider theactionintegralf(u) =uJu˙.Here we notethatJisminusof thatin[16].Then wehavef ∈C1(E,R).Define the bounded self adjoint linear operatorL:E →Eby:=f′(u)v,∀u,v ∈E,where<·,·>is the scalar product inE. By direct calculation,we have

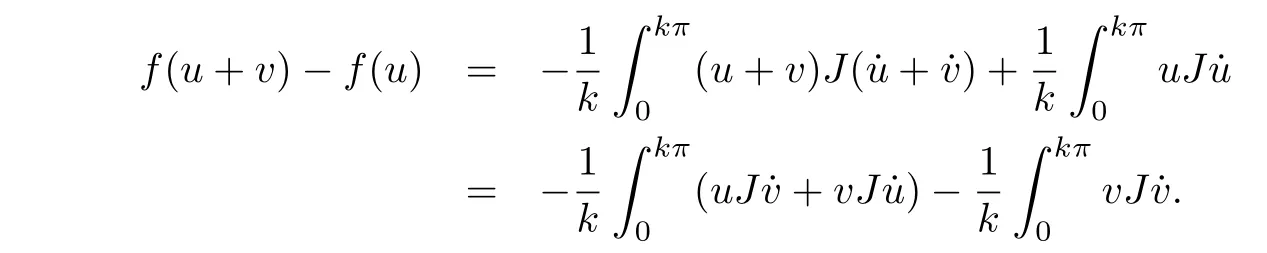
Noticing that

and

we obtain

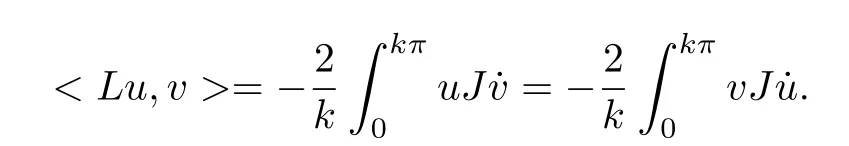
Lemma 2.1Ifu ∈Sis a critical point off|S,withf(u)>0,then there exists aλ>0,such that

Obviously,there exists aλ,such that ˙u=λJH(u). The positivity ofλeasily follows(see(2.5)). In the following we shall show that=H′(u)w, ∀w ∈E.

Note thatH(Pu) =H(u). Differentiatinguon the two sides,we haveH(Pu) =PH(u). ThenH′(un(t+π))=H′(Pun(t))=PH′(un(t)),sinceun ∈E1. ThenH′(un)∈E1,which implies

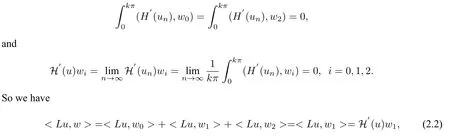
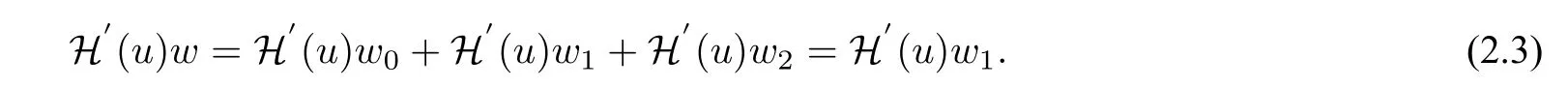
From(2.2)and(2.3),=H′(u)w,∀w ∈E. The Lemma is proved.

Ifusatisfies(2.1),thenu˜(t)≡u()is a solution ofu˙ =JH′(u)of periodkπλ,andu˜(t+λπ) =P˜u(t). Ifuhas minimal periodkπ,then ˜u(t)has minimal periodkπλ.

It is easy to know that the existence ofngeometrically distinctPcyclic symmetric closed characteristics on Σ is equivalent to the existence ofncritical points off|S, say,u1,u2,··· ,un,such thatf(ui)>0,ui(t)̸=uj(t+θ)fori ̸=j,θ ∈R/(kπZ)anduihas minimal periodkπ.

LetZ={u ∈S|f′|S(u)= 0,f(u)> 0}. If we consider the functionfand the manifoldSin the spaceE,then we have:

Lemma 2.2Ifu ∈Z,thenf(u)≥.

Recall thatH(αz)=α2H(z),by differentiatingαon the two sides,then we have

Ifu ∈Z,we can know there exists aλ>0,such that ˙u=λJH′(u)from lemma 2.1. Then

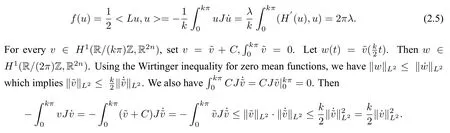
Hence,from(2.5),we have

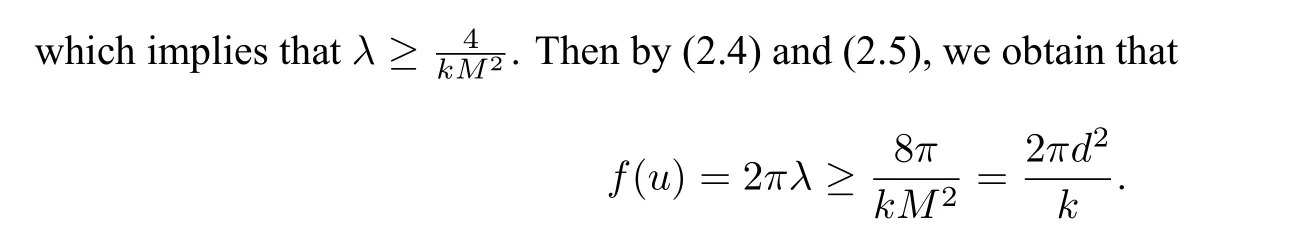
The Lemma is proved.

If we consider the functionfand the manifoldSin the spaceE1,then we have a stronger result:

Lemma 2.3Ifu ∈Z,thenf(u)≥.

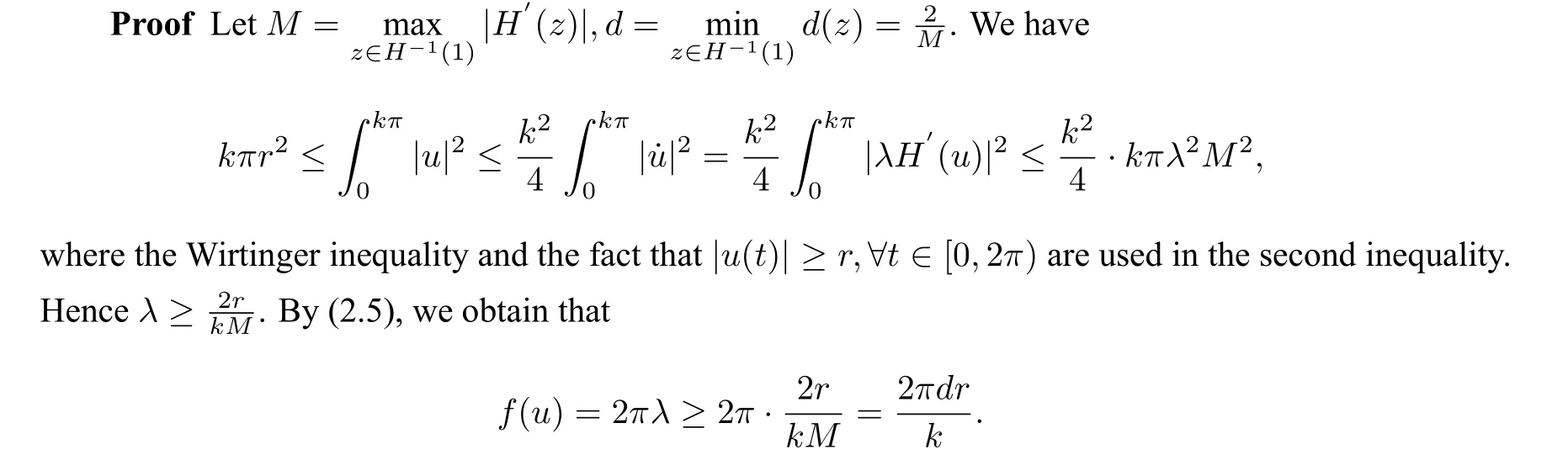
The Lemma is proved.

The following lemma is a consequence of Lemma 2.3.

Lemma 2.4Ifu ∈Zandf(u)<πdr, thenucan not be any multiple iteration of someu1∈Z,which implies thatuhas minimal periodkπ.

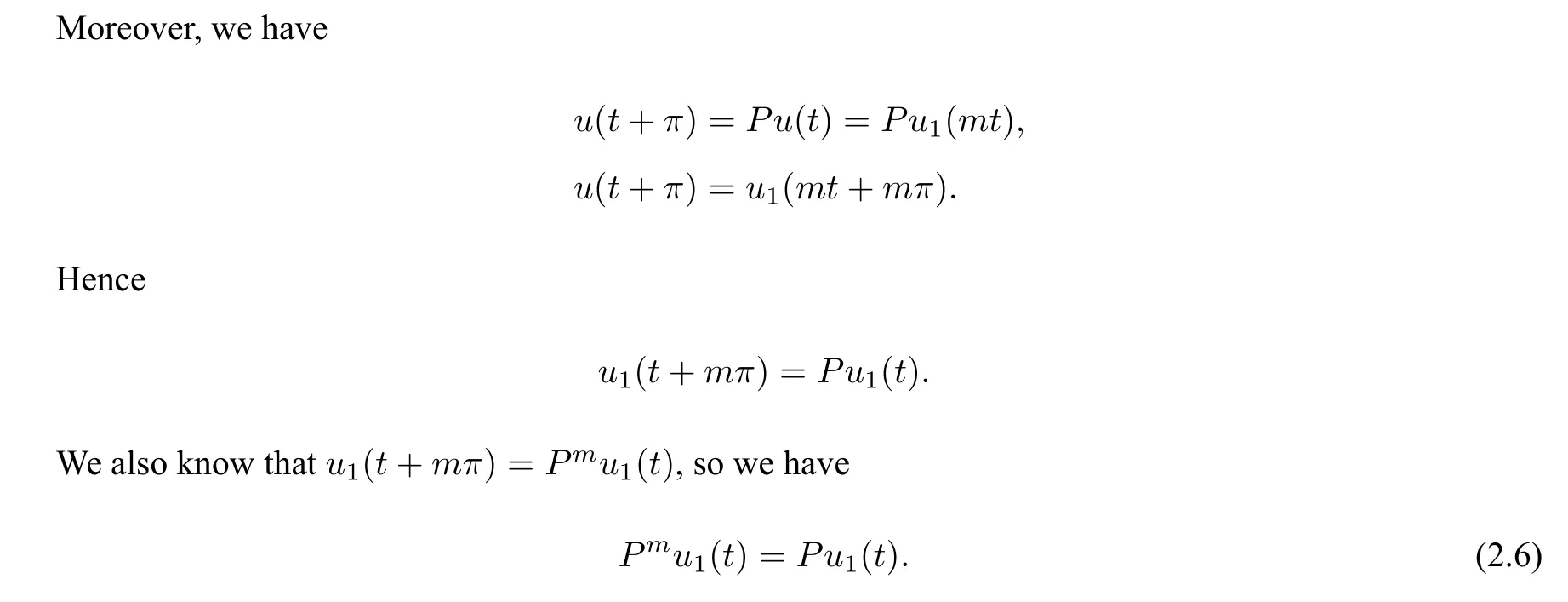
If 2≤m ≤k, we can multiply the left and right sides of (2.6) byPk−m. Then we getu1(t) =Pk−m+1u1(t)by usingPk=I2n. Thus,there exists anl ∈N such thatk −m+1 =lk. However,if 2≤m ≤k,we have 1≤lk ≤k −1,which is impossible.

Ifm ≥k+1,we have

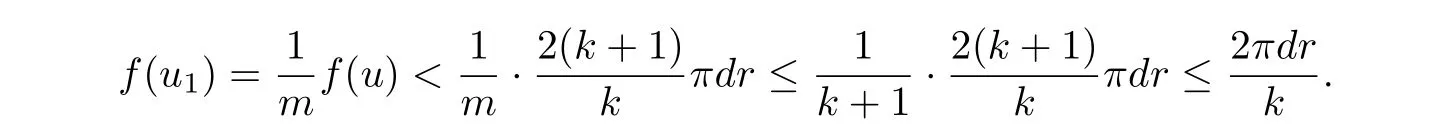
It is impossible, becausef(u1)>by Lemma 2.3. Souhas minimal periodkπ. The Lemma is proved.

Now, we define a pseudo index (see [2], [3]) and make use of the invariance offandSthrough theS1actionS1×E1→E1: (θ,u(t))→u(t+θ),u ∈E1,θ ∈S1, whereS1= R/(kπ)Z. Letφm= ek2mtJam+ek2(−m+2−k)tJa−m+2−k, whereal ∈R2nforl=m,−m+2−k,σm=f(φm),m ∈N,m ≡1(modk). Let

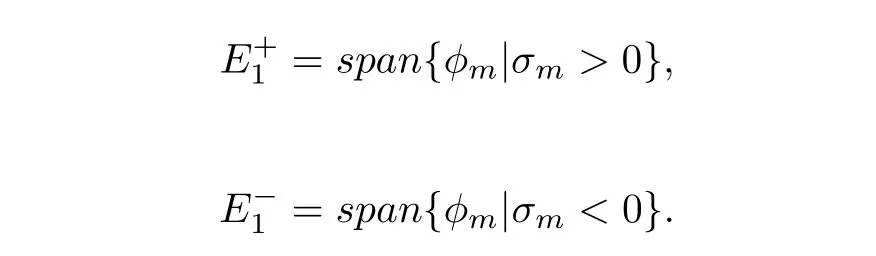
Obviously,E1=is the orthogonal decomposition ofE1with regard to the functionalf(see[33]). LetGbe aC1manifold ofE1,radially diffeomorphic to the unit sphere ofE1,invariant under theS1action. LetU:E1→E1be a self adjoint linear equivariant isomorphism such thatU()⊂.Denote by∪the set of these isomorphisms. Leth:G →Gbe an equivariant homeomorphism satisfying that there exist a continuous mapg:G →R+and aU ∈∪such thath −gU|Gis compact. Denote by ΓGthe family of all suchh,which is a group. LetVbe the family of closed,S1invariant subsets ofE1.ForA ⊂G,A ∈V,the pseudo index is defined as

whereiis theS1index introduced by Benci[3]. Recall the following results:

Proposition 2.1AssumeG1andG2areC1manifolds radially diffeomorphic to a sphere ofE1and invariant under theS1action. Letp:G1→G2be the radical projection fromG1toG2. Then

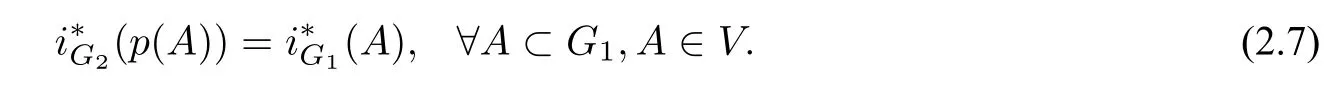
Proposition 2.2LetHh ⊂E1be a 2hdimensional invariant subspace andHh ⊕W=E1. Then forA ⊂G,A ∈V,

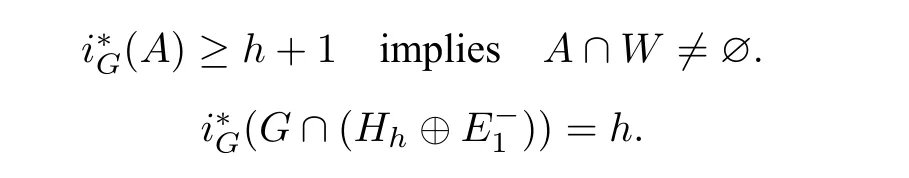
Supposef|Gsatisfies the Palais Smale condition. LetZc={u ∈G|f′|G(u) = 0,f(u) =c}. We define

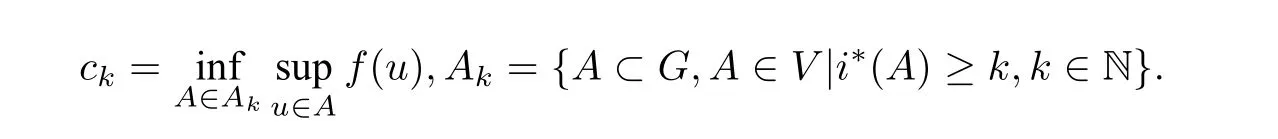
Thenckis a critical value off|G. Moreover ifc=ck+1=···=ck+p,theni(Zc)≥p. It is the famous Minimax principle. And it is known thatf|Ssatisfies the Palais Smale condition,see[4]and[16].

Let us considerSR={u ∈E1||u|2=R2},which is aC1manifold radially deffeomorphic to a sphere ofE1, invariant under theS1action.f|SRverifies the Palais Smale condition. So we can apply the Minimax Principle toSR. Let us denote bya1,a2,··· ,anthe firstncritical values off|SRof minimax type. We have the following lemma.

Lemma 2.5Forf|SRwe havea1=···=an=.

By Proposition 2.6,we havei∗(An)=n. We can immediately know that

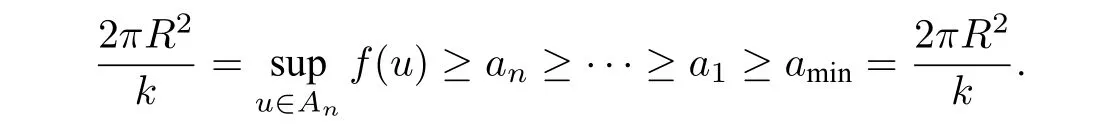
The Lemma is proved.

Now,we can prove Theorem 1.2.

Let

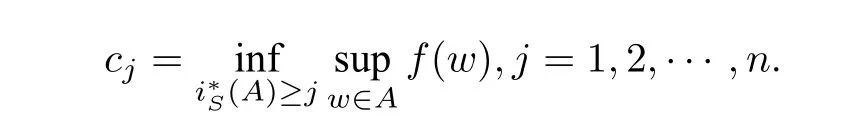
We know thatc1,c2,··· ,cnare critical values off|S,andcj ≥. For everyu ∈SR,there exists a uniqueλsuch thatλu ∈Sandλ ≤1. ForA ∈S ∩V,we have

wherepis the radical projection fromStoSR. By(2.7),we see that

So

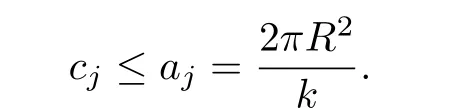
By the assumption thatR2<(k+1)dr,we have

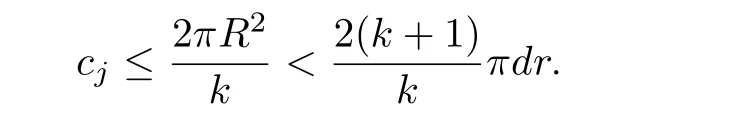
From Lemma 2.4,ifcj=f(uj),then we can easily knowujis a critical point off|Sandujhas minimal periodkπ.

Theorem 1.2 is proved.