杨纪鹏，夏 烨，闫业祥，孙利民,2

(1.同济大学 土木工程学院，上海 200092;2.同济大学 土木工程防灾国家重点实验室，上海 200092)

土木工程结构在强地震荷载作用下由于结构损伤而引起系统参数突变，其包括结构刚度、阻尼以及描述系统行为的其他参数，因而考虑参数时变特性的结构系统识别得到越来越多的重视。

Yang等[1]提出自适应最小二乘法，该方法在识别结构参数时需要观测结构的位移、速度和加速度，实际中地震作用下结构的位移和速度是很难观测到的，而加速度是容易测得的物理量。

Yang等[2-3]提出自适应扩展卡尔曼滤波法，该方法基于扩展卡尔曼滤波法(extended Kalman filter，EKF)，在状态误差协方差矩阵中引入自适应矩阵，追踪突变结构参数。扩展卡尔曼滤波是用泰勒展开式去线性近似状态估计值和量测观测值。该理念处理非线性模型的思想清晰，滤波过程简单有效；但该方法也有明显的缺陷：①进行泰勒级数近似展开时需要计算雅克比矩阵(Jacobian)，但对于有些非线性系统，其Jacobian矩阵不易计算；②通常EKF仅保留一阶精度，若要提高到二阶精度则要计算海塞矩阵，计算过程更加复杂；③因仅保留一阶精度，通常需要较高的采样频率才能保证滤波效果。

雷鹰等[4]将静力凝聚法与扩展卡尔曼滤波法相结合，识别结构参数，同时定量识别结构节点损伤程度，该方法基于扩展卡尔曼滤波，对于复杂系统求解Jacobian矩阵比较困难。

Julier等[5]根据确定性采样提出的无迹卡尔曼滤波(unscented Kalman filter，UKF)以Unscented变换来近似计算系统状态的后验均值和协方差，相较于直接近似非线性函数本身，前者更容易实现，UKF能以至少二阶精度逼近任何非线性系统。但传统UKF存在协方差矩阵开方时矩阵奇异的数学问题。谢强等[6-7]提出奇异值分解(singular value decomposition,SVD)计算状态误差协方差矩阵的平方根，但效果欠佳。

池传国等[8]提出一种基于M估计的强跟踪SVD-UKF算法。该算法利用M估计理论，对异常新息数据进行“筛选”，保留有用新息，剔除有害新息，有效避免由卫星信号野值引起的粗差对强跟踪SVD-UKF算法的鲁棒性影响。

王小旭等[9-10]提出强追踪无迹卡尔曼滤波器，该方法克服了传统UKF无法追踪时变结构参数的缺点，但其计算过程中需要计算状态预测误差协方差矩阵的平方根，其数值稳定性较差。

Van der Merwe等[11]提出平方根卡尔曼滤波，该方法基于UKF的算法框架，以协方差矩阵的平方根代替协方差矩阵进行递推运算。该算法避免了时间状态预测时协方差矩阵开方计算，但在滤波结果更新协方差矩阵平方根时，需要进行乔里斯基分解一阶更新，其对矩阵的正定性的要求与UKF一样高，并没有从根本上解决数值计算时不稳定的问题。

张玉峰等[12]基于平方根滤波的思想，对传统的Sage-Husa自适应滤波算法进行了改进，并与平方根无迹卡尔曼滤波(square root unscented Kalman filter,SRUKF)结合，该算法能直接对非线性系统的状态方差矩阵和噪声方差矩阵的平方根进行递推与估算，确保状态和噪声方差矩阵的对称性和非负定性，但文中仍需计算量测矩阵的Jacobian矩阵，未引入强追踪滤波因子，不能有效追踪时变系统参数。

叶浩泽等[13]在标准的平方根UKF算法上，首先改用了球型无迹变换对权系数以及Sigma点进行计算选取；其次改进了SRUKF中平方根矩阵的分解方法；同时在预测误差协方差矩阵中引入了自适应衰减因子。该文中也需计算观测矩阵的Jacobian矩阵，且文中计算强追踪滤波因子的方法并不适用于土木结构系统参数识别。

李敏等[14]提出一种改进的强跟踪平方根无迹卡尔曼滤波(strong tracking square root unscented Kalman filter，STSRUKF)导航方法，采用一种改进的平方根分解方法，改善了滤波器的稳定性。同时，基于强跟踪滤波器理论，引入多重自适应衰减因子调节协方差矩阵，使得滤波器具有强跟踪能力。数值模拟表明该方法效果并不好，同时该方法需要计算量测矩阵的Jacobian矩阵，文中所使用的强追踪滤波因子算法也不适用于土木结构系统参数识别。

基于以上问题，本文提出改进的强追踪平方根无迹卡尔曼滤波方法(modified strong tracing square root unscented Kalman filter ，MSTSRUKF)。该方法首先改进了协方差矩阵平方根计算方法，根据协方差定义直接使用QR分解计算其平方根，避免使用乔里斯基分解一阶更新，使协方差矩阵平方根计算过程无条件数值稳定；其次，引入量测矩阵Jacobian矩阵的等价形式进行计算，对于非线性量测系统，可避免求解Jacobian矩阵，减小计算工作量，使该方法更具有普适性；最后，引入强追踪滤波因子，根据土木工程结构参数特点，调整滤波因子矩阵对应项的比值，使该方法在引起较小参数波动的情况下即可识别到时变结构参数。

1 改进的平方根强追踪无迹卡尔曼滤波

1.1 标准的SRUKF算法

考虑如下的离散非线性系统模型

(1)

式中：f(·)为非线性状态函数；h(·)为非线性量测函数；Xk+1为n维系统状态向量；Zk+1为m维量测向量；uk为s维系统输入向量；wk为n维系统过程噪声;vk+1为m维量测噪声;wk和vk+1均为互不相关的零均值高斯白噪声。且有

E(wk)=0,cov(wk,wj)=Qkδkj,

E(vk)=0,cov(vk,vj)=Rkδkj,

cov(wk,vj)=0

(2)

式中：Qk和Rk分别为系统过程噪声协方差矩阵和系统量测噪声协方差矩阵;δkj为kronecker函数。基于UKF的平方根无迹卡尔曼滤波(SRUKF)标准流程如下。

步骤1初始化状态X0，状态误差协方差矩阵平方根S0

(3)

(4)

(5)

步骤3时间预测更新

(6)

(7)

(8)

(9)

步骤4量测更新

(10)

(11)

(12)

(13)

(14)

步骤5滤波结果更新

(15)

(16)

U=KkSZ

(17)

Sk+1|k+1=cholupdate{Sk+1|k,U,-1}

(18)

上述计算过程中用到的权值参数计算如下

(19)

式中:λ=α2(n+κ)-n;α为决定Sigma点在先验均值附近扩展程度的主要尺度因子，通常取1×10-3<α≤1;β为第二个尺度因子，用于强调后验协方差计算的第0个Sigma点的权重;κ为三级比例因子，通常取κ=3-n;n为状态向量的维数;qr(·)为QR分解;cholupdate(·)为乔里斯基分解一阶更新;上标T为矩阵的转置。

1.2 改进的SRUKF算法

1.2.1 改进的时间预测状态向量误差协方差矩阵平方根计算

在标准的SRUKF算法中，由式(8)与式(9)计算状态向量时间预测的误差协方差矩阵的平方根，即式(9)可等价描述为

(20)

式(9)通过cholupdate计算Sk+1|k时，要求式(20)等式右边必须是正定的，其要求与标准的UKF中计算误差协方差矩阵平方根一样严格，实际运算中由于舍入误差的影响，很难保证矩阵的正定性，为此根据时间预测误差协方差矩阵的定义

(21)

Sk+1|k=rT

(22)

又由式(21)推导得到

(23)

(24)

(25)

数值分析结果表明，式(25)对计算结果影响不大。

而李敏等提出如下的时间预测误差协方差矩阵的计算方法

(26)

(27)

数值分析结果表明，式(26)、式(27)所提出的协方差计算方法参数识别结果并不理想。故本文提出如下协方差矩阵平方根计算方法

(28)

再通过式(24)计算Sk+1|k。

1.2.2 改进的量测误差协方差平方根计算

同理，式(12)、式(13)可改进为

(29)

(30)

1.2.3 改进的滤波更新协方差矩阵计算

计算滤波结果更新状态向量误差协方差矩阵平方根时，式(17)、式(18)可等价描述为

(31)

这要求式(31)等式右边必须是正定的，由于舍入误差的影响，很容易使该部分失去正定性，因此还需对状态估计误差协方差矩阵平方根的计算做如下改进。

根据状态估计误差协方差的定义

(32)

将式(16)代入式(32)得

(33)

同时，式(1)中的量测方程可写为

Zk+1=Hk+1Xk+1+Vk+1

(34)

(35)

将式(34)、式(35)代入式(33)可得

(36)

式中，I为单位矩阵。

由于Vk+1与其他向量不相关，根据协方差矩阵定义，由式(36)可推导得到

(37)

根据状态向量时间预测误差协方差矩阵平方根计算的改进方法，可得到改进的滤波更新状态估计协方差矩阵的平方根计算方法

(38)

(39)

1.2.4 量测矩阵的改进

对于复杂的非线性结构，若观测向量与状态向量之间为非线性关系，为避免计算Jacobian矩阵，可使用量测矩阵Hk+1的等价形式。根据定义，状态预测自协方差矩阵Pk+1|k，输出预测自协方差矩阵PZZ,k+1和输出预测互协方差矩阵PXZ,k+1可写为式(40)～式(42)的形式

(40)

则可求得量测矩阵的等价形式为

(43)

1.3 强追踪滤波算法

要使滤波器式(16)成为强追踪滤波器的一个充分条件是实时在线调整增益矩阵Kk，使得

(44)

(45)

(46)

(47)

(48)

(49)

(50)

式中:tr[·]为矩阵的迹；l≥1为弱化因子；Γk+1为实际输出残差序列，可以表示为

(51)

设引入强追踪渐消因子后的时间预测误差协方差矩阵的平方根表示为Sk+1|k,new，计算出强追踪滤波因子后，式(28)、式(24)表示的时间预测误差协方差矩阵的平方根计算方法可更新为

(52)

(53)

根据以上推导，MSTSRUKF算法步骤可以描述为

步骤1根据式(3)、式(4)初始化系统状态;

步骤3时间预测更新，根据式(6)、式(7)、式(28)、式(24)计算时间预测状态向量及协方差矩阵的平方根;

步骤4量测更新，根据式(10)、式(11)、式(29)、式(30)、式(14)计算量测更新

步骤5计算渐消因子矩阵，更新时间预测误差协方差矩阵的平方根；根据式(43)计算量测矩阵Jacobian矩阵等价形式，根据式(46)～式(51)计算渐消因子矩阵，根据式(52)、式(53)计算引入渐消因子后的时间预测误差协方差矩阵的平方根;

步骤6滤波更新,根据式(15)计算增益矩阵，根据式(16)计算k+1时刻状态后验估计值；引入渐消因子后，k+1时刻状态预测协方差矩阵根据式(54)～式(56)计算

(54)

(55)

(56)

2 数值算例验证

2.1 三自由度线性结构系统

首先考虑一个三自由度线性结构系统遭受地震激励，其运动方程可以写为

(57)

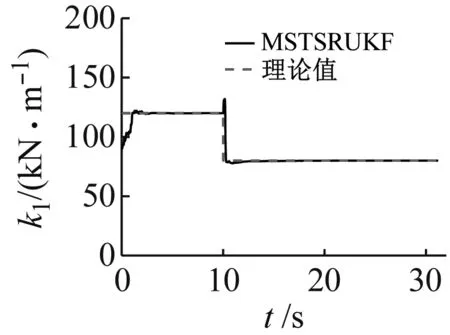
本算例中，取m1=m2=m3=1 000 kg，k1=120 kN/m，k2=120 kN/m，k3=60 kN/m。c1=c2=c3=0.6 kN·s/m，地震激励选取El Centro地震波，采样频率100 Hz，地震持续时间31.2 s。

为模拟实际观测中噪声的干扰，在模拟的量测加速度数据中加入5%RMS(root mean square)的高斯白噪声，然后使用低通滤波去除加速度时程中的高频成分，滤波截断频率为20 Hz，为了验证MSTSRUKF在识别线性结构参数突变时的有效性，设定当t=10 s时:结构一层刚度由k1=120 kN/m突变到k1=80 kN/m，二层刚度k2=120 kN/m突变到k2=80 kN/m，三层刚度k3=60 kN/m突变到k3=40 kN/m；结构一层阻尼由c1=0.6 kN·s/m突变到c1=0.7 kN·s/m，二层阻尼c2=0.6 kN·s/m突变到c2=0.65 kN·s/m，三层阻尼c3=0.6 kN·s/m突变到c3=0.65 kN·s/m。状态向量初值取为X0=[0,0,0,0,0,0,90,90,50,0.3,0.3,0.3]T

结构参数识别结果,如图1所示。结构各层位移识别结果,如图2所示。

若以1～10 s为第一阶段，10.0～31.2 s为第二阶段，不同阶段参数最终识别结果如表1所示。

由图1、图2及表1可以看出，本文提出的MSTSRUKF：①能够快速有效地识别突变的结构参数；②由于刚度参数的数量级远大于阻尼参数，其在协方差矩阵中起主要作用，故刚度参数识别精度高于阻尼参数，且阻尼参数震荡幅度更大，收敛速度慢于刚度参数；③能够准确估计出结构位移时程；④由各个阶段最终识别结果看出，即使加入5%白噪声，最终收敛精度仍然很高，刚度参数识别误差不大于0.2%，阻尼参数识别误差不大于4%，具有较高的鲁棒性；⑤所提出算法数值稳定，不存在因矩阵奇异而计算中断的问题。

表1 线性系统时变参数识别结果Tab.1 Time-varying parameter identification results of linear system

2.2 三自由度Bouc-Wen模型系统

考虑一个三自由度剪切型框架结构，底层采用Bouc-Wen滞回模型，受地震荷载激励，其运动方程可写为

(59)

(a)

本算例中，取m1=450 kg，m2=400.5 kg，m3=350.5 kg；k1=20.5 kN/m，k2=23.5 kN/m，k3=23.5 kN/m；c1=0.205 kN·s/m，c2=0.255 kN·s/m，c3=0.255 kN·s/m；α=0.2，β=2，γ=1，n=1，由于该模型参数的冗余性，n不作为待识别参数。地震激励选取El Centro地震波，采样频率100 Hz，地震持续时间31.2 s。

(a)

本文中认为地震输入已知，观测量为各层绝对加速度。为模拟实际观测中噪声的干扰，在模拟的量测加速度数据中加入5%RMS的高斯白噪声，然后使用低通滤波去除加速度时程中的高频成分，滤波截断频率为20 Hz，为了验证MSTSRUKF在识别非线性结构参数突变的有效性，设定当t=15 s时：结构一层刚度由k1=20.5 kN/m突变到k1=14 kN/m，结构二层刚度k2=23.5 kN/m突变到k2=16 kN/m，三层刚度k3=23.5 kN/m突变到k3=16 kN/m。状态向量初值取为X0=[0,0,0,0,0,0,0,16,16,16,0.16,0.16,0.16,0.16,1.6,0.8]T

结构参数识别结果，如图3所示。结构各层位移识别结果，如图4所示。第一层滞回曲线及滞变位移识别结果，分别如图5、图6所示。

(a)

(a)

图5 第一层滞回曲线识别结果Fig.5 Hysteric loop estimation results of 1st floor

图6 第一层滞变位移识别结果Fig.6 Hysteric displacement estimation results of 1st floor

若以1～15 s为第一阶段，15.0～31.2 s为第二阶段，不同阶段参数最终识别结果,如表2所示。

由图3、图4、图5、图6以及表2可以看出，本文提出的MSTSRUKF：①对于非线性系统具有良好的识别效果，能较为准确地识别各层位移；②能够有效识别到参数突变，刚度参数在经过短暂震荡后很快收敛到真值；③根据先验知识调整阻尼项在渐消因子中对应μk值，阻尼项经较小幅度的震荡后，也很快收敛到真值；④由于刚度参数的数量级远大于阻尼参数的数量级，故刚度参数的识别精度高于阻尼参数；⑤结构参数突变后，描述Bouc-Wen模型系统的参数识别精度有所降低，最高误差达到-11.19%；⑥所提方法数值计算稳定，对于强非线性系统仍能稳定、有效运行。

表2 Bouc-Wen模型系统时变参数识别结果Tab.2 Time-varying parameter identification results of Bouc-Wen model system

2.3 三自由度杜芬结构系统

考虑一个三自由度剪切型杜芬系统遭受地震激励，其运动方程可以写为

(60)

本算例中取m1=m2=m3=1 000 kg，c1=c2=c3=0.6 kN·s/m，k1=120 kN/m，k2=120 kN/m，k3=60 kN/m，kd1=200 kN/m3，kd2=200 kN/m3，kd3=-50 kN/m3。地震激励选取El Centro地震波，采样频率100 Hz，地震持续时间31.2 s。

本文中认为地震输入已知，观测量为各层绝对加速度。为模拟实际观测中噪声的干扰，在模拟的量测加速度数据中加入5%RMS的高斯白噪声，然后使用低通滤波去除加速度时程中的高频成分，滤波截断频率为20 Hz，为了验证MSTSRUKF在识别非线性结构参数突变的有效性，设定当t=15 s时，结构一层刚度由k1=120 kN/m突变到k1=100 kN/m，结构二层刚度k2=120 kN/m突变到k2=100 kN/m。状态向量初值取为X0=[0,0,0,0,0,0,90,90,50,0,0,0,0.3,0.3,0.3]T。

结构参数识别结果,如图7所示，结构各层位移识别结果,如图8所示。

(a)

(a)

若以1～15 s为第一阶段，15.0～31.2 s为第二阶段，不同阶段参数最终识别结果,如表3所示。

表3 Duffing系统时变参数识别结果Tab.3 Time-varying parameter identification results of Duffing system

由图7、图8及表3可以看出，本文提出的MSTSRUKF：①能够准确估计Duffing系统位移时程；②能够有效追踪到结构刚度突变，并很快收敛到真值；③根据先验知识调整阻尼项在渐消因子中对应μk值，阻尼参数微小震荡后快速收敛到真值；④与位移三次方相关的刚度参数识别误差略微偏大，最大误差为5.54%；⑤计算过程数值稳定，不存在因数学计算不稳定而意外终止的问题。

3 结 论

针对土木工程结构地震作用下时变参数识别问题，提出改进的强追踪平方根无迹卡尔曼滤波算法。算法克服了传统UKF及SRUKF协方差矩阵平方根递推过程中数值计算不稳定的问题，使递推过程无条件数值稳定；其次使用量测矩阵Jacobian矩阵的等价形式，避免复杂系统求解Jacobian矩阵，简化计算方法，扩展该方法的应用范围；最后引入强追踪滤波技术，实现时变结构的参数识别。数值分析结果表明：

(1)线性系统数学模型相对简单，其时变参数识别结果优于非线性系统，因刚度参数与阻尼参数数量级相差较大，刚度参数识别结果优于阻尼参数。

(2)对于Bouc-Wen模型系统，由于控制滞回特性的参数较多，而系统对不同参数的敏感性也不同，故应科学选取敏感参数的初值及协方差矩阵中对应的元素值，避免识别过程中系统发散。

(3)对于杜芬系统，与位移三次方对应的刚度参数识别结果精度低于与一次项对应的刚度参数，说明其对系统的影响程度不如一次项对应的刚度参数。

(4)对于时变参数的线性系统和非线性系统，所提方法均能较好地识别结构参数，结构状态预测结果在初始阶段有一定误差，待参数收敛后预测结构状态也与真实状态吻合良好。

(5)在数值模拟过程中，所提出的算法数值计算稳定，最终识别结果表明本文提出的方法在避免求解Jacobian矩阵后能够准确识别结构参数。

针对时时参数突变的情况因收敛需要过程，当结构刚度、阻尼以及控制滞回特性的参数变化在合理范围内时，所提算法能够收敛；本算法确保了递推过程计算的稳定性，但实际工程中观测量数目远小于结构的自由度数目，实际应用效果还需进一步验证。