马文君, 孙亮亮

(1. 兰州工商学院 经济学院, 兰州 730101; 2. 西北师范大学 数学与统计学院, 兰州 730070)

0 引 言

自Lazer等[1]提出并研究了如下吊桥方程的大振幅周期振荡问题

以来, 关于吊桥方程解的存在性和行波解性质的研究已有很多结果[2-4]. 近年来, 随着自然界中随机干扰或不确定因素对确定性系统的影响, 关于随机动力系统的研究也得到广泛关注[5-9], 例如, Crauel等[7]对非线性扩散方程、 Navier-Stokes方程、 非线性波方程等证明了其随机吸引子的存在性. 但在实际应用中, 吊桥系统不可避免地受随机噪声的影响. 本文考虑如下带有加性噪声的吊桥方程：

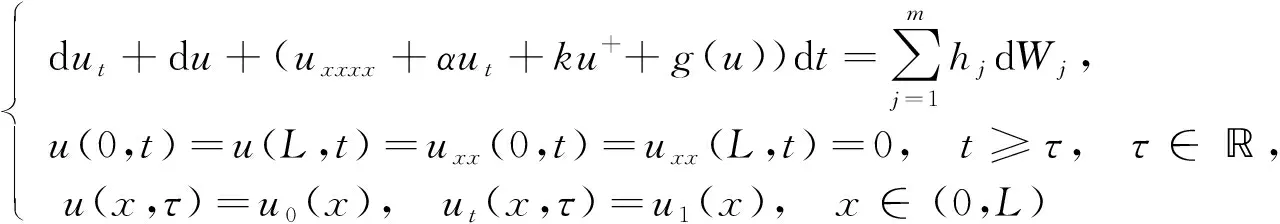
(1)

随机吸引子的存在性, 其中: (x,t)∈(0,L)×[τ,+∞);u=u(x,t)表示桥面在竖直方向的振动,u+为其正部, 即

k>0表示弹性系数,ku+是桥面在垂直方向振动时由Hooke定律得到的恢复力.根据Hooke定律, 当吊桥被拉长时, 桥梁将受到大小与位移成正比的恢复力作用;α是黏性阻尼系数; 对任意的s∈, 非线性函数g∈C2(,)满足下列假设:

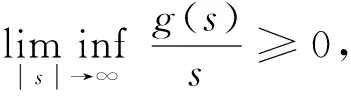
(2)

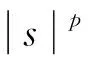
(3)

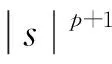
(4)

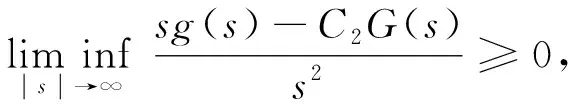
(5)

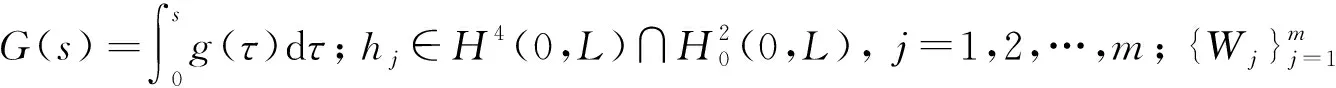
Θ={ω=(ω1,ω2,…,ωm)∈C(,m):ω(0)=0}

被赋予紧的开拓扑, P是相应的Wiener测度, F是Θ上的Borelσ-代数.记W(t,ω)∶=ω(t), 且定义

θtω(·)=ω(·+t)-ω(t),t∈,ω∈Θ.

文献[10]研究了带有加性噪声的随机强阻尼Plate方程随机吸引子的存在性; 文献[11]讨论了带白噪声的可拉伸吊桥方程随机吸引子的存在性; 文献[12]研究了带线性记忆和弱阻尼的问题(1)拉回吸引子的存在性. 但对带有加性噪声的随机吊桥方程(1)解的渐近行为研究目前尚未见文献报道. 由于当系统受到加性噪声干扰时, 状态空间的有界子集不再保持不变， 为建立系统的渐近紧性带来困难. 因此, 研究带有加性噪声的随机吊桥方程(1)随机吸引子的存在性有一定的理论意义. 本文讨论带有加性噪声的阻尼吊桥方程(1)解的渐近行为, 用算子分解技巧, 通过对方程的解进行先验估计, 给出随机动力系统的一致渐近紧性, 从而证明方程(1)随机吸引子的存在性.

1 预备知识

设(X,‖·‖X)是一个具有Borelσ-代数B(X)的可分的Hilbert空间, D是X上所有调和随机集的集合, (Θ,F,P,(θt)t∈)是一个度量动力系统.

定义1[5]设(Θ,F,P,(θt)t∈)是一个度量动力系统, 对于映射φ:+×Ω×X→X, 若其为(B(+)×F×B(X),B(X))-可测的, 且对所有的s,t∈+,x∈X和ω∈Θ均满足下列条件:

1)φ(0,ω)x=x;

2)φ(s,θtω)∘φ(t,ω)x=φ(s+t,ω)x.

则称φ为随机动力系统(RDS).进一步, 如果对于t≥0,ω∈Θ,φ关于x是连续的, 则称φ为连续随机动力系统.

定义2[5]如果随机集A∶={A(ω)}ω∈Θ∈X满足下列条件, 则称A为随机动力系统φ的D-随机吸引子:

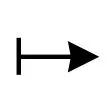
2) A是φ-不变的, 即对所有的T≥0及a.e.ω∈Θ,φ(t,ω,A(ω))=A(θtω);

3) A吸引所有调和随机集B∈D, 即对所有的a.e.ω∈Θ, 有

其中dist(·,·)表示X中两个子集之间的Hausdorff半距离.

命题1[5]设φ是X中关于(Θ,F,P,(θt)t∈)的连续随机动力系统, 若存在一个随机紧集K(ω), 使得对任意非随机有界集{B(ω)}ω∈Θ, 有

则φ存在一个D-随机吸引子A={A(ω)}ω∈Θ, 其中

2 解的存在唯一性

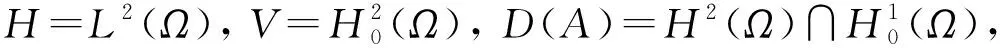
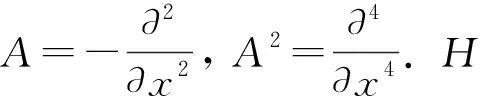
显然有V⊂H=H*⊂V*, 其中H*,V*分别是H,V的对偶空间.

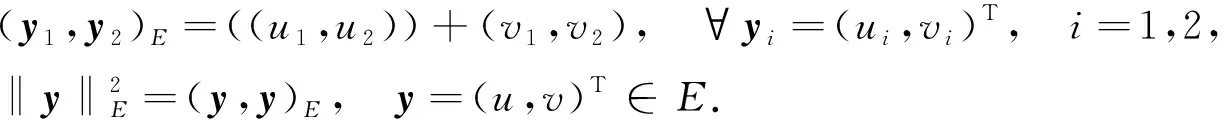
(6)

此外,Lp(Ω)范数记为‖·‖p.由Poincaré不等式, 得

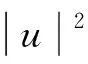
其中λ1是一个正常数.

为将问题(1)转化为带有随机参数的确定性系统, 并证明其可生成一个随机动力系统.下面考虑Ornstein-Uhlenbeck方程

dzj+zjdt=dWj(t),j={1,2,…,m}

(7)

和Ornstein-Uhlenbeck过程

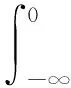
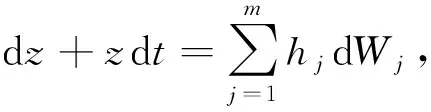
(8)

则

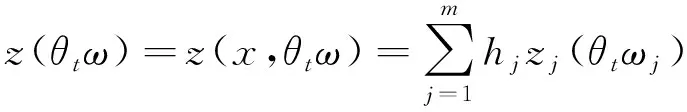
(9)

是式(8)的一个解.

‖z(θtω)‖≤eε|t|r(ω), e-ε|t|r(ω)≤r(θtω)≤eε|t|r(ω),

‖A(l)z(θtω)‖≤eε|t|r(l)(ω), e-ε|t|r(l)(ω)≤r(l)(θtω)≤eε|t|r(l)(ω),

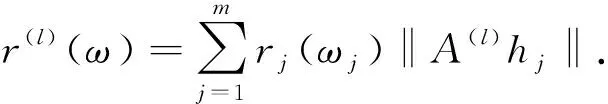
将方程(1)转化为

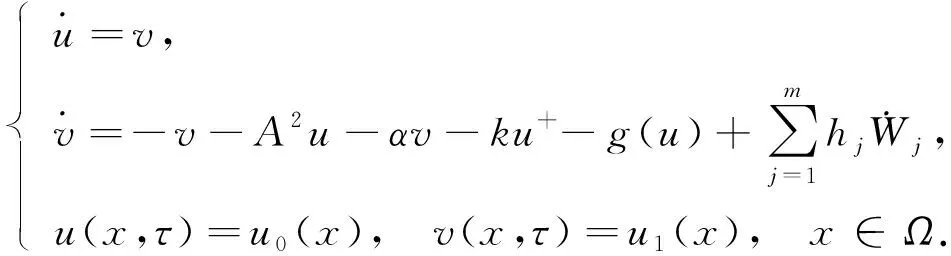
(10)

设

可得方程(10)的矩阵形式：

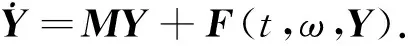
(11)

设φ1=u,φ2=v-z(θtω), 方程(10)可转化为如下等价系统：

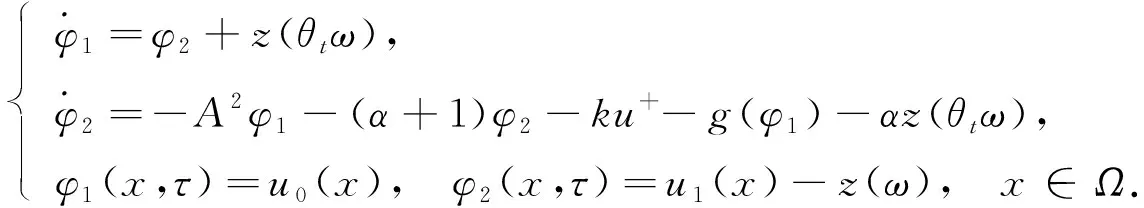
(12)

设φ=(φ1,φ2)T, 可得

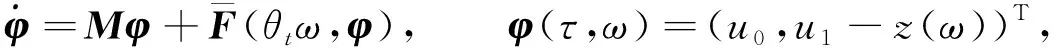
(13)

其中

由文献[15]可知, -M是E上的C0-半群e-Mt的无穷小生成元, 且函数F(·,ω):E→E关于φ局部Lipschitz连续.所以, 由文献[15]中发展方程解的局部存在唯一性经典半群理论, 可得随机偏微分方程(13)有唯一解, 例如, 对a.s.φ(τ,ω)∈E, 有

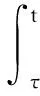
对a.e.ω∈Θ,T>0, 下列结论成立:

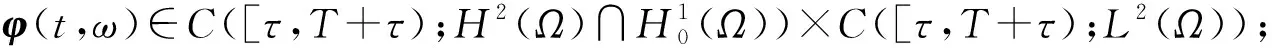
(ii)φ(t,φ(τ,ω))关于t和φ(τ,ω)连续;

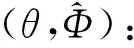
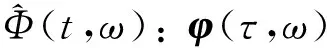
(14)

因此, 通过变换

(15)

也可生成一个与方程(10)相应的随机动力系统.

3 随机吸引子的存在性

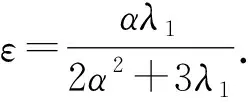
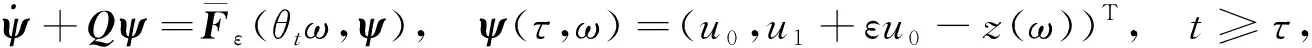
(16)

其中

定义映射

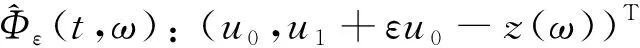
则

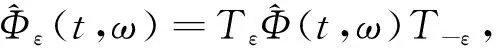
(17)

设υ(t)=(υ1,υ2)T=(u(t),v(t)+εu(t))T是系统(13)的解, 则式(13)可化为

υt+Qυ=G(θtω,υ),υ(-τ,ω)=(u0,u1+εu0)T,t≥τ,

(18)

其中

下面证明算子Q在E中的正定性.

引理2对任意的υ=(υ1,υ2)T∈E, 有

证明: 因为Qυ=(ευ1-υ2,(A2-ε(α-ε+1))υ1+(α-ε+1)υ2)T, 由Poincaré不等式可得

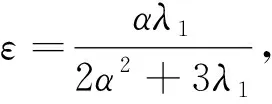
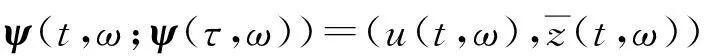
‖ψ(-1,ω;ψ(τ,ω))‖E≤r0(ω),τ≤T(B).

(19)

且对τ≤t≤0,

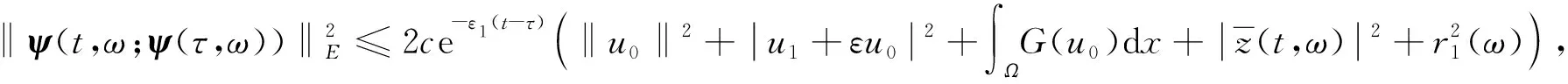
(20)

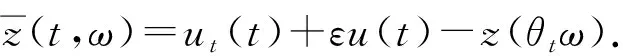
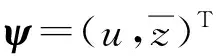
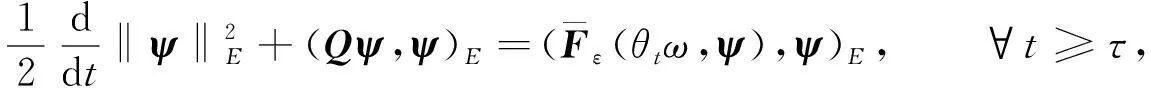
(21)

其中

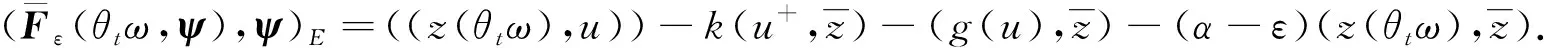
(22)

由Cauchy-Schwarz不等式和Young不等式, 有

(23)

(24)

(25)

结合式(3)～(5), 可得

故∃M1>0, 使得

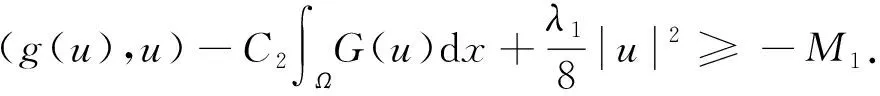
(27)

由式(26),(27), 得

由式(21),(23)～(25),(28)和引理2, 得

利用引理1, 有

其中

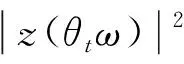
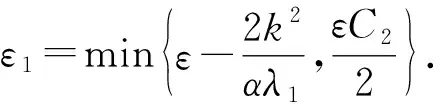
由引理1, 有

其中

令

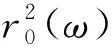
证毕.

为得到正则性估计, 本文利用文献[8,16-17]中的方法, 将系统(1)的解u(t)分解成u=y1+y2, 分别满足下列方程:

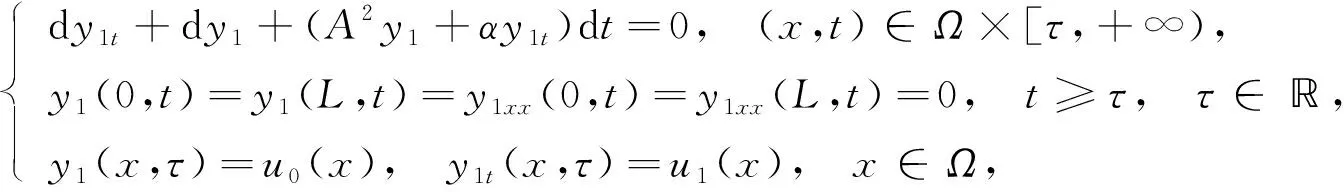
(30)

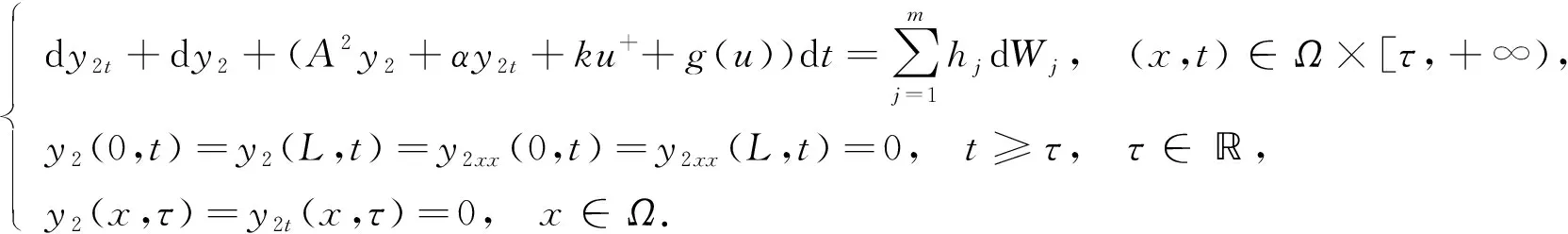
(31)

下面对方程(30)和方程(31)的解进行先验估计.

引理4设B是E上的非空有界子集, 若条件(2)～(5)成立, 则对任意的(u0,u1+εu0)T∈B, 有

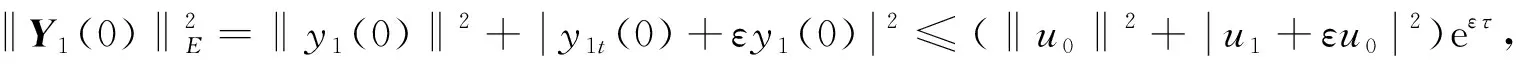
(32)

并存在一个随机半径r2(ω)>0, 使得对P-a.s.ω∈Θ, 有

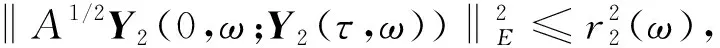
(33)

其中Y1=(y1,y1t+εy1)T和Y2=(y2,y2t+εy2-z(θtω))T分别满足方程(30)和方程(31).

证明： 用初值为(u0,u1+εu0)T的y1t+εy1与方程(30)在L2(Ω)上做内积.由引理2可得式(32).下面证明式(33), 从而可得解(y2,y2t)更高的正则性.设Y2=(y2,y2t+εy2-z(θtω))T, 方程(31)可转化为

Y2t+QY2=H(Y2,ω),Y2(τ)=(0,-z(ω))T,t≥τ,

(34)

其中

用AY2与方程(34)在E上做内积, 得

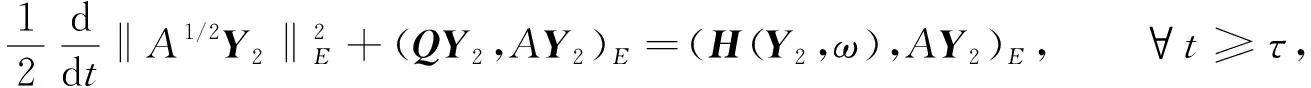
(35)

其中

由引理2可知,

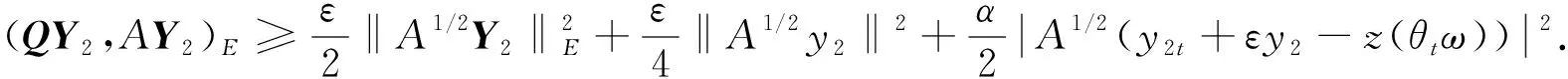
(37)

下面对式(35)右边的各项进行如下估计:

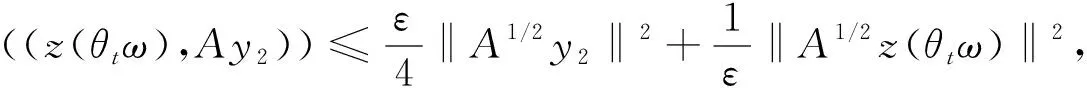
(38)

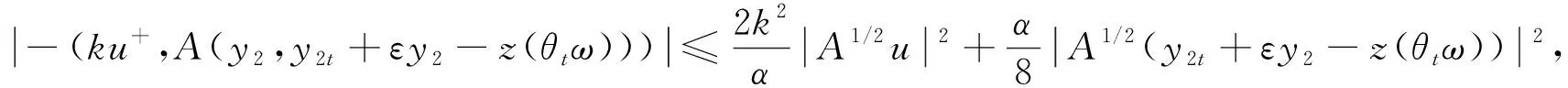
(39)

由式(3),(20)及Sobolev嵌入定理知,g′(u)在L∞上一致有界, 即存在常数M2>0, 使得

|g′(u)|L∞≤M2.

(41)

由Young不等式和式(41), 得

其中Cs>0是一个嵌入常数.

结合式(35)～(42),(20), 对所有的τ≤T(B), 均有

由Gronwall引理和引理1可得

令

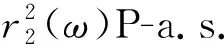
证毕.

从而有

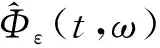
dist(Φε(t,θ-tω)B,B1/2(ω))→0, P-a.s.

因此, 由式(15)所确定的随机动力系统Φε(t,ω)有一致渐近紧的吸引集B1/2(ω)∈E, 即随机动力系统Φε(t,ω)在E中一致渐近紧.

定理1假设式(2)～(5)成立, 则式(15)所确定的随机动力系统Φε(t,ω)有一个非空紧的D-随机吸引子A.

证明: 结合引理3、 引理4及命题1可知结论成立.