基于广义概率假设密度的多目标运动估计方法研究

2021-09-18余萌徐琰珂胡茄乾

航空兵器 2021年4期

余萌徐琰珂胡茄乾

摘要：面向空对空作业的发展需求，提出了一种基于广义概率假设密度的多目标运动估计方法。在Faster-RCNN方法基础上引入多尺度分析，并利用改进K-means方法对观测目标进行粗聚类，以此为前置输入，提出了基于广义泊松分布的概率假设密度滤波器，将聚类信息纳入滤波估计的权重更新中，增强了对变阵群目标的跟踪时效性。仿真结果表明，本文方法在没有初始聚类信息的先验知识下，依然能够完成对多目标的识别分类与跟踪，且精度优于现有的集群目标运动估计方法。

关键词：多目标运动估计; K-means聚类; 目标识别; 概率假设密度; 态势感知

中图分类号：TJ765; TP391.4 文献标识码： A 文章编号：1673-5048（2021）04-0037-06

0 引言

为适应日趋复杂的作战环境，多飞行器协同作战方案逐渐成为当前空中打击作业的热点方向。美国海军研究的低成本无人机蜂群（Drone Swarm）技术已经成功完成了多次实地测验，初步实现了无人机集群编队飞行与快速机动。俄罗斯新的S-70“猎人”（Okhotnik-B）重型隐形无人机成功伴飞苏-57，突出了战斗支援角色，旨在扩大战斗机的能力。这些无人机集群和无人机与有人机的编队，大大加强了空中打击力量的突防能力，为国土防空增加了新的压力。为实现对空中集群目标的有效防御，需要发展具有集群目标针对性的跟踪应对技术。

通常情况下，多飞行器集群目标都是按照一定的编队飞行方式进行空中作业，通过在复杂背景中进行机动目标集群聚类分析，可以实现对集群目标的阵群态势粗估计。传统的无监督聚类方法（如谱聚类、 K-means等）容错性差，且对初始值非常敏感，尤其对有噪声的机动目标聚类效果欠佳。本文在Faster-RCNN方法基础上引入多尺度分析，并利用改进K-means方法对观测目标进行了粗聚类，将集群目标的态势粗估计分为群目标识别以及类别数估计两部分，旨在提升集群目标运动估计精度的同时，增强估计方式的灵活性。

在群目标识别方面，本文以Faster-RCNN为基础进行改进。经典R-CNN[1]采用了Selective Search算法来提取图像中可能存在的兴趣区域（Regions of Interest），之后对每个提取区域采用标准的卷积神经网络（CNN）进行分类。在R-CNN后， 2015年提出的Fast-RCNN[2]采用兴趣区域池化来共享计算量较大的部分，以此提高模型的效率，随后发展的Faster-RCNN[3-4]是建立在Fast-RCNN基础上的一个完全可微分模型，在卷积层后使用Region Proposal Network（RPN）生成一系列靶块，对其进行裁剪过滤后利用softmax判断靶块属于前景还是后景，同时使用另一分支进行靶块修正，凝练较为精确的提议（Proposal）。 Faster-RCNN与Fast-RCNN的明显区别就是使用了RPN代替了选择性搜索来产生提议，并强调提议的CNN网络与目标识别的CNN共享。 Faster-RCNN同时将特征抽取、候选区域提取、边界框回归、分类整合到了一个网络当中，使目标识别的综合性能得到了很大改进。

分类态势粗估计可以为多目标跟踪提供前置输入。传统的多目标跟踪方法有联合数据关联方法（JPDA）[5]、假设目标跟踪方法（MHT）[6-7]等，这些方法多利用先验假设，将集群目标出现的几类运动情景综合考虑（如遮挡、虚报或目标合并等）。考虑到目标以集群为单位运动时，目标的数量、阵群会发生变化，而传统方法对阵群可变的目标运动估计解释性不足[8]，本文基于随机有限集合思想的扩展目标概率假设密度（ET-PHD）滤波方法[9]，面向阵群可变的多目标运动估计提出相应的方案。核心方法是利用先验的粗聚类信息为ET-PHD方法提供聚类初值，并引入广义泊松分布来增强对概率强度估计的解释性，进而提高对阵群可变的目标跟踪品质。航空兵器 2021年第28卷第4期

余萌，等：基于广义概率假设密度的多目标运动估计方法研究

1 多目标编队的态势粗估计

1.1 基于Faster-RCNN的多目标识别

多目标识别是多目标运动估计的前置环节，能够为后续态势感知、运动估计提供基礎数据。考虑应用背景，本文选择深度学习方法——Faster-RCNN，对组网结构进行量体裁衣，发展了基于Faster-RCNN的集群目标识别方法，使用的敏感器为机载单目相机。

1.1.1 数据库选择与组建

选择的深度学习训练集为DOTA（A Large-Scale Dataset for Object Detection in Aerial Images）[10]，是武汉大学与华中科技大学联合制作的遥感图像数据集，共有2 806张遥感图像以及15个类别。经过适当修改，该数据库最终包含了直升机、无人机、客机、战斗机以及怀疑目标这五个类别，其中在怀疑目标类别中归属了诸如热气球、翼伞、鸟类等空中目标。

1.1.2 基于改进Faster-RCNN的空中多目标识别

考虑空中作业环境中前/后景差异相比地面场景中更为明显，特征的颗粒度更高，因此，从计算代价角度考虑，并不需要生成一系列稠密的靶块进行前/后景判断。为此，本文对Faster-RCNN方法进行了改进，在原图尺度上采用谱残差方法替换原方法中候选靶块生成，利用多个尺度下的局部图像显著性表征，通过非极大抑制实现候选框生成，如图1所示。

这种方法在前/后景差异明显的情况下可以在保证识别精度的同时，大幅降低训练所需计算代价。在获得Proposal的特征图后，分类时采用全连接层与softmax计算每个Proposal的类别归属，并输出5×1的概率向量。同时，利用边框回归得到每个Proposal的位置偏移量，实现更准确的目标检测。由于本文对数据库进行了重新设计，因此对整体组网进行了重新训练，并未使用流行的迁移学习方法。

利用Faster-RCNN能够实现基于单目相机的目标识别，但考虑方法目的与实时性，在此仅将其作为集群目标的初始信息，其余集群运动估计及编队态势提取与此环节独立。图2为使用Faster-RCNN的飞行目标检测示意图。

利用改进Faster-RCNN进行算法测试，结果表明，基于显著性多尺度RPN表征的简化方法与原Faster-RCNN并无明显差异，但改进方法的训练成本大幅降低，在未来出现未编目飞行目标时，重训练以及参数调整的灵活性优势明显。

1.2 多目标隶属估计

通过Faster-RCNN可以输出目标的群类别以及在图像中的矩心位置，其中，群类别是以概率向量来描述，一个典型的输出结果如下：

Proposal={[k1， m1]， [k2， m2]， …， [kN， mN]}（1）

式中： k=[p1， p2， …， pK]T为概率向量， [pi|i∈K]为属于其中某类的概率， K为类别总个数; m=[μ， ν]为群目标在图像中的矩心位置，此处为目标所属检测框的矩心。以Proposal提供的目标识别为基础，结合K-means方法[11]提出了目标快速聚类方法，其主要思想是在K-means方法的基础上引入分类评估置信率函数，即

wj=∑x∈Djln（Djx-mj）∑k∈K∑x∈Dkln（Dkx-mk）（2）

式中： Dj为第j个类别中的目标聚类集; wj为相对应的权重参数。在K-means迭代过程中，根据置信率评估结果剔除置信过小的分类，算法的伪代码实现流程图如图3所示。

相比经典K-means方法，本文方法的计算复杂度从O（itn）上升至O（k·itn）。该方法能够通过置信率实时估计来增强对观测噪声的抗干扰能力，相比经典方法在鲁棒性上有一定提升，图4所示为观测噪声影响情况下的估计结果示例。

红色棱柱为在编队在相机像平面下的跟踪估计结果，机载相机的观测结果以粒子点描述。将运动目标分为3个编队，并在不同信噪比的条件下比较经典K-means与Proposal-K-means两种方法的估计结果。

Proposal-K-means群目标隶属估计方法 P-K-means（K， M， x， D）

输入：（k1， m1），（k1， m2）D1

k2， m3D2， …， kK， mMDV∥Proposal 提供的分类及像素位置

For （k， m）∈（K， M）

针对每个Proposal：

选择K个聚类点作为初始聚类中心： mi， i=1， …， D

重复

初始化sj=0， j=1， …， D， nj=0， j=1， …， D

For x∈D

j=argminfdist（x， mf）

分配相应的x到类别j：

sj=sj+x; nj=nj+1;

End

mj=sj/nj， j=1， …， k

直至mj迭代收敛。

对每一个分类评估其置信率：

wj=∑x∈DjlnDjx-mj/∑k∈K∑x∈DklnDkx-mk

剔除wj过小的分类

输出聚类结果： K-， M-

图4（a）中编队数目为3个，由图可知，经典K-means能够准确跟踪编队目标的像素位置信息，仅在仿真末段编队1与编队2较为接近时，出现6处估计精度欠佳的情况（规定估计结果与编队内任一成员的像素欧式距离大于60即为精度欠佳）。本文所提出的Proposal-K-means在无编队数目这一先验信息情况下，与经典K-means的估计结果无显著差异。由图4（b）可以看出，即便在已知编队数量为3个的前提下，估计精度欠佳的比例仍达到了31%，主要归因于当观测噪声与目标的像素位置比较接近时，仅采用欧式距离作为判据法并不能做出准确的区分。相比经典K-means方法， Proposal-K-means在群矩心位置的估计精度上提升明显，如图4（c）所示，其估计精度欠佳的比例为18%（相比经典K-means降低了40%），其主要是因为Proposal-K-means将编队的隶属信息作为输入，并通过实时监测分类的置信率来剔除隶属信息不可靠的估计结果，即相比经典K-means引入了审查环节，因此能够在一定程度上减少估计精度欠佳的分类。图4（d）其群矩心位置估计与真实情况具有较为明显的差异，聚类精度仅为60%，此结果也符合仿真预期，因为K-means本质上仍对噪声抗干扰能力不足，需要使用集群运动估计方法来提升目标运动状态估计的鲁棒性。

由于Proposal能够提供给K-means分类以及矩心的初值，故将经典K-means从有监督学习转变为无监督学习，更加符合任务对自主性与灵活性的需求。

2 多目标运动估计

ET-GM-PHD方法面向的是单个目标可产生多观测量的跟踪场景。在本文的应用背景下，若将单阵群视为扩展目标（即能够产生多个观测量的目标），便可以使用ET-GM-PHD滤波方法进行集群目标運动估计。 PHD滤波方法与传统滤波方法的主要区别是去除了计算量庞大的测量信息与运动目标进行匹配关联的步骤，采用多目标随机有限集合的概率分布一阶矩进行状态估计，将定义在多目标状态空间上的后验概率密度映射到单目标的状态空间上，并将单目标状态空间分布定义为概率假设密度（Probability Hypothesis Density， PHD），又称目标强度[12]。由于在目标强度分布的迭代估计过程涉及到集合积分的运算，其算力需求过大， Vo等人提出了GM-PHD方法[13]，其利用加权高斯混合模型刻画该目标的强度分布，并通过与Kalman滤波器相似的预测步与更新步操作，实现时间上的传递，显著降低了PHD算法的许用算力。

以Dk|k-1， Dk表示离散时间下k时刻目标状态强度的预测值与更新值，则有

Dk|k-1（x）=∫pS， k（ζ） fk|k-1（x|ζ）Dk-1（ζ）dζ+γk（x）

Dk（x）=LZk（x）Dk|k-1（x）

LZk（x）=[1-pD， k（x）]+

∑z∈ZkpD， k（x）gk（z|x）κk（z）+∫pD， k（ε）gk（z|ε）Dk|k-1（ε）dε （3）

式中： fk|k-1（x|ζ）为目标状态转移方程; ζ为前一步状态; Zk为第k步的目标观测集; g（z|x）为观测后验概率; κk（z）为噪声干扰强度; γk（x）为新生目标强度，对应可能出现的干扰弹等战术策略; pD， k为目标的检测率，该数值根据设备及应用场景可能会有所变动; LZk（x）为伪量测似然率，代表了预测与更新过程的强度传递。

在针对扩展目标（Extended Target）提出的ET-PHD滤波框架中， Mahler[14]认为单个目标具有多个“散射中心”，体现在量测上则认为每个目标可以产生多个目标量测，并且该假设服从泊松分布x～λ（λ为期望目标量测数），则LZk（x）可以描述为

LZk（x）=1-（1-e-λ（xk））pD（xk）+e-λ（xk）pD（xk）·

∑p∠Z′kωp∑W∈pλ（xWk）dW∏zk∈Wg（zk|x）σkκk（zk）（4）

式中： p∠Zk为对目标测量集的聚类分割; ωp为聚类方式p在所有可能聚类方式中所占的比重; W为量测单元子集; W为子集W中元素个数; σk为期望噪声个数; dW为分割单元因子：

dW=δ|W|， 1+Dk|k-1e-λ（x）λ（x）|W|pD， k（x）∏zk∈Wg（zk|x）σkκk（zk）（5）

以上针对扩展目标的跟踪算法在应用至集群目标运动估计问题时有两处值得商榷：（1）集群目标的数目强度函数与基于泊松分布假设的单目标散射强度分布不可一概而论; （2）原ET-GM-PHD方法采用了量测子集遍历分割，虽然Mahler在理论上证明了ET-PHD方法的收敛一致性[12]，但显然不能直接应用到实时性要求较高的集群目标运动估计中。考虑以上因素，本文对式（4）中的强度函数进行重新梳理，引入了上述的态势粗估计信息作为前置输入，指导阵群组合的候选，并将PHD滤波中的泊松分布假设进行拓展，设计广义泊松分布：

pdf=λke-λk！pdf=λnmnm！H（λ， n， m， c）（6）

式中： pdf为概率密度函数（probability density function）; H（λ， n， m， c）为新引入的态势响应函数，可以描述为

H（λ， n， m， c）=eλ1（m， n）if c=c1

eλ2（m， n）if c=c2

eλi（m， n）if c=ci

eλD（m， n）if c=cD （7）

式中： ci（i=1， 2， …， D）为编队态势编目信息; λ1， 2， …， D为泊松分布均值; n， m为相关参数。将经典泊松分布进行式（6）的拓展，旨在赋予强度分布函数的灵活度，其强度估计可以根据编队态势进行灵活调整，相比原方法，更强调对变阵群目标跟踪质量的提升。结合式（5）～（6），式（3）可重新梳理为

Lz（x）=1-pD（xk， n， m）+e-λ（n， m， c）pD（xk， n， m）+e-λ（n， m， c）pD（xk， n， m）∑p∠z′kωp∑W∈pλxWkdW·

∏zk∈Wφzkxkσkκk（zk）（8）

式中：

m（j）S， k|k-1=Fk-1m（j）k-1

P（j）S， k|k-1=Qk-1+Fk-1P（j）k-1FTk-1

其中： Fk-1为状态转移雅克比矩阵，本文对空中机动目标的动力学建模沿用标准的辛格（Singer）模型[15]。由于两个高斯混合集的加法封闭，即两者相加仍为高斯混合集，因此，目标后验强度预报值可以描述为一个整体高斯混合集形式，即

式中： Jk|k-1=Jk-1+Jγ， k。结合观测量的强度估计增量，对目标后验强度的估计可以描述为

Dk（x）=（1-pD， k）Dk|k-1（x）+∑z∈ZkDD， k（x， z）（10）

式中：DD， k（x， z）=Dk|kx|Z（k）。基于观测量的目标后验强度估计，同样利用高斯混合集近似该分布：

DD， k（x， z）=∑Jk|k-1j=1ω（j）k（z）N（x;m（j）k|k（z）， P（j）k|k）（11）

式中：

ω（j）k（z）=pD， kω（j）k|k-1q（j）k（z）κk（z）+∑Jk|k-1l=1ω（l）k|k-1q（l）k（z）

q（l）k（z）=N（z; Hkm（l）k|k-1， Rk+HkP（l）k|k-1HTk）

m（l）k|k（z）=m（l）k|k-1+K（l）k（z-Hkm（l）k|k-1）

P（l）k|k=[I-K（l）kHk]P（l）k|k-1

K（j）k=P（j）k|k-1HTkHkP（l）k|k-1HTk+Rk-1

此處所提方法与原始ET-GM-PHD方法的不同之处，在于利用了广义泊松分布对权值进行重新梳理。具体而言，基于Proposal-K-means得到的分类信息，即zW∈Zp∠Zk，针对每个高斯核函数进行权值计算：

Γ（j）=e-λ（n， m（j）k|k-1， c）（λ（n， m（j）k|k-1， c））|W|

φ（j）W=N（zW;HWm（j）k|k-1， HWP（j）k|k-1HTW+RW）

Φ（j）W=φ（j）W∏zk∈W1σkκk（zk）

ω（j）k=Γ（j）pD， kΦ（j）Wω（j）k|k-1（12）

最终将权值、估计均值与方差按经典高斯混合集处理方法进行合并，并保留权重大于0.5的均值估计，最终输出最终估计结果。

3 算法仿真与分析

为验证本文所提方法有效性，编写了一套多目标运动模拟软件。

在仿真软件中，用户可以自由导入运动目标的物理模型，定义编队个数及队内隶属成员信息。如图5所示，在软件中导入了3个编队，执行100 s的编队飞行任务，飞行速度为300～330 km/h，跟踪机保持300 km/h的匀速飞行，编队1～3中分别设置了4， 3， 3个成员。

结合仿真软件，对本文算法进行完整的仿真分析，并选择了Farin等人提出的基于L1优化的多目标跟踪方法[16]、标准ETPHD方法[17]、 BURNULLI-I方法[13]、标

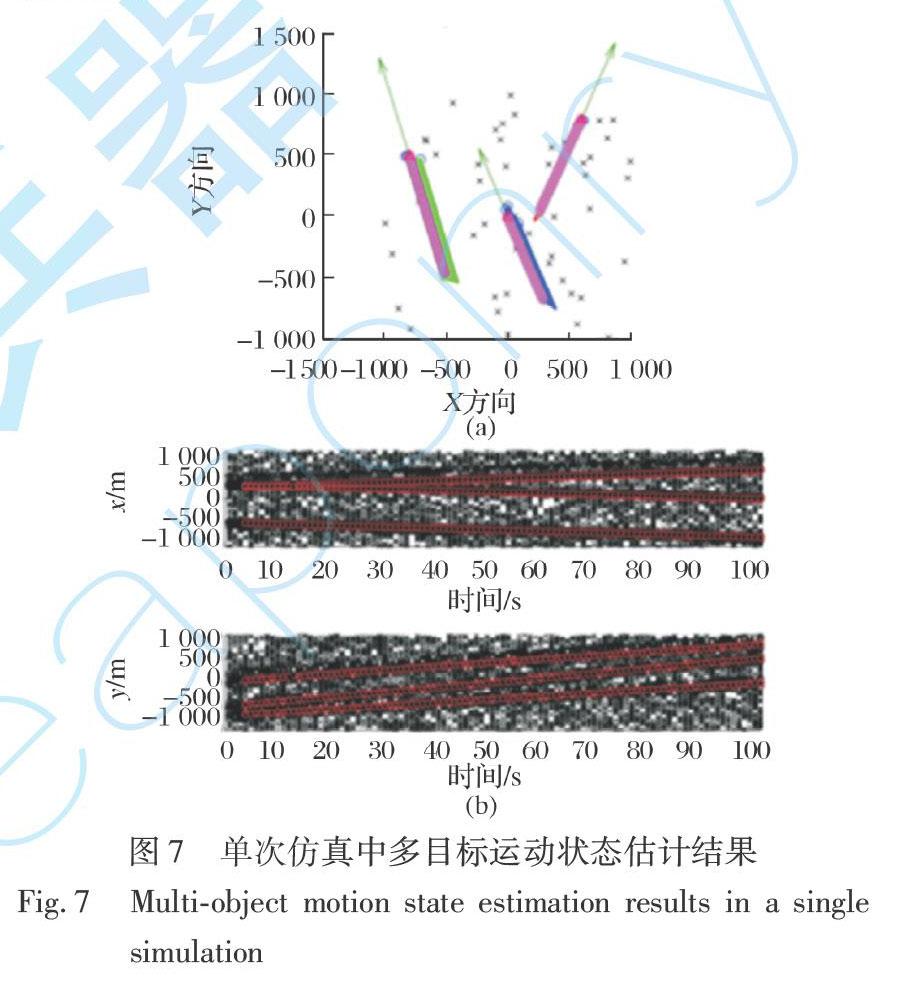
准MHT方法[18]以及基于标准K-means的ET-GM-PHD方法作为对比方案，利用标准最优次模式分配距离（Optimal Sub-Pattern Assignment， OSPA）[19]作为评估依据，进行蒙特卡洛仿真验证，仿真打靶次数为100次。 OSPA是一种多目标运动估计性能评价的一致性度量方法，其将真实轨迹与估计轨迹之间的误差分为距离误差与关联误差两个部分，进而综合衡量估计误差大小。单次仿真中集群目标二维运动轨迹及估计结果，如图6～8所示。

图6为本次仿真的集群目标运动轨迹在X-Y平面下的投影，其中横纵坐标等比缩放至-1 000～ 1 000。将观测信噪比调整至0.4，图7（a）为添加了观测噪声后本文方法的运动状态估计结果，其中加粗线为最终估

计轨迹; 图7（b）为在噪声影响下的状态估计时间历程。

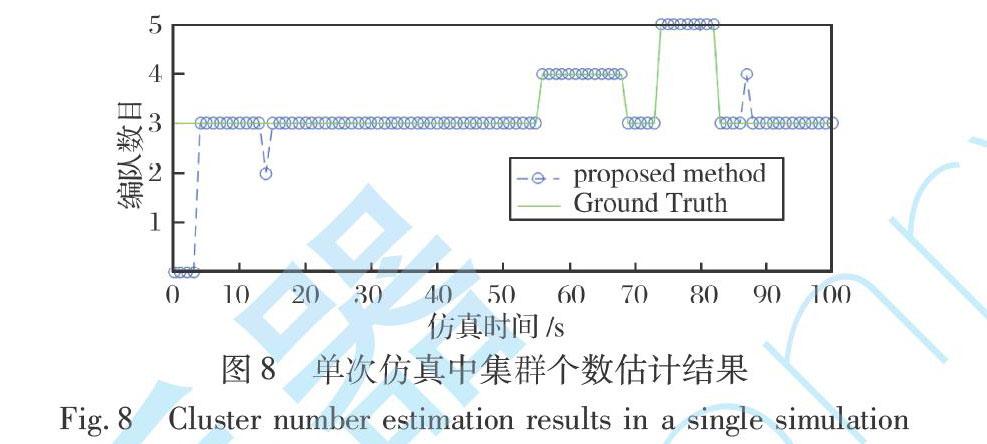
可以看出，本文方法在该次仿真中能够全程跟踪3个编队的运动状态，目标的状态估计OSPA精度均在300以内，优于其他5种对比算法，并且能够实现其编队数目态势的实时估计，在一定程度上也体现了算法的优势。本文算法在前100步仿真中仅出现2次编队数量估计错误，如图8所示。

与上述多目标跟踪方法的比较结果如图9所示。

本文方法的OSPA指标能够稳定在300以内，且估计变化幅度最低，表明其估计精度与稳定性均优于其他的多目标跟踪方法。本文算法在75%的时间内（离散时间统计）能够准确捕捉所有目标的编队数目态势信息。本文方法

的实时性略微差于其他5类方法，但并无显著差异，此结果也符合仿真预期。因本方法增加了对编队态势估计环节，在一定程度上降低了算法的实时性，

取而代之的是能够更加快速地捕捉到集群目標编队态势的变化。此点优势更加贴近实际空对空作业的任务需求，体现了算法的优势。

4 结论

本文面向空对空作业背景下多目标的实时跟踪任务需求，发展了集群目标运动的估计方法。针对集群目标态势粗估计方面，组建了目标识别数据库，将多尺度显著性分析引入Faster-RCNN，提出了集群目标检测方法，在此基础上结合改进K-means发展了集群态势粗估计方案。其次，以ET-GM-PHD方法为基础，引入广义泊松分布概念对PHD滤波过程中权重更新进行重新梳理，提高了对阵群可变的集群目标跟踪精度。最终，本文面向研究的应用背景编写了多目标运动与跟踪仿真软件，并对算法进行了仿真分析，与现有的主流多目标跟踪方法相比，本文方法虽在实时性上略显劣势，但运动估计精度提升明显。

参考文献：

[1] Krizhevsky A， Sutskever I， Hinton G. ImageNet Classification with Deep Convolutional Neural Networks[J]. Communications of the ACM， 2017， 60（6）： 84-90.

[2] Girshick R. Fast R-CNN[C]∥Proceedings of the IEEE International Conference on Computer Vision， 2015： 1440-1448.

[3] Ren S Q， He K M， Girshick R， et al. Faster R-CNN： Towards Real-Time Object Detection with Region Proposal Networks[C]∥ Proceedings of the 28th International Conference on Neural Information Processing Systems， 2015： 91-99.

[4] Fattal A-K， Karg M， Scharfenberger C， et al. Saliency-Guided Region Proposal Network for CNN Based Object Detection[C]∥IEEE 20th International Conference on Intelligent Transportation Systems （ITSC）， 2017.

[5] Roecker J A. A Class of Near Optimal JPDA Algorithms[J]. IEEE Transactions on Aerospace and Electronic Systems， 1994， 30（2）： 504-510.

[6] Blackman S S. Multiple Hypothesis Tracking for Multiple Target Tracking[J]. IEEE Aerospace and Electronic Systems Magazine， 2004， 19（1）： 5-18.

[7] Svensson D， Wintenby J， Svensson L. Performance Evaluation of MHT and GM-CPHD in a Ground Target Tracking Scenario[C]∥12th International Conference on Information Fusion， 2009： 300-307.

[8] Chong C Y， Mori S， Reid D B. Forty Years of Multiple Hypothesis Tracking-A Review of Key Developments[C]∥21st International Conference on Information Fusion， 2018.

[9] Granstrom K， Lundquist C， Orguner O. Extended Target Tracking Using a Gaussian-Mixture PHD Filter[J]. IEEE Transactions on Aerospace and Electronic Systems， 2012， 48（4）： 3268-3286.

[10] Xia G S， Bai X， Ding J， et al. DOTA： A Large-Scale Dataset for Object Detection in Aerial Images[C]∥ IEEE/CVF Conference on Computer Vision and Pattern Recognition， 2018.

[11] Jain A K. Data Clustering： 50 Years Beyond K-Means[J]. Pattern Recognition Letters， 2010， 31（8）， 651-666.

[12] Mahler R P. A Theoretical Foundation for the Stein-Winter “Pro-bability Hypothesis Density （PHD）” Multitarget Tracking Approach[R]. Eagan： Lockheed Martin Corporation， 2000.

[13] Vo B-T， Vo B-N， Cantoni A. The Cardinality Balanced Multi-Target Multi-Bernoulli Filter and Its Implementations[J]. IEEE Transactions on Signal Processing， 2009， 57（2）： 409-423.

[14] Mahler R. Divergence Detectors for Multitarget Tracking Algorithms[C]∥ Proceedings of SPIE-The International Society for Optical Engineering， 2013， 8745（4）： 241-253.

[15] 魏喜慶，顾龙飞，李瑞康，等.基于Singer模型的高超声速飞行器轨迹跟踪与预测[J]. 航天控制， 2017， 35（4）： 62-66.

Wei Xiqing， Gu Longfei， Li Ruikang， et al. Trajectory Tracking and Prediction of Hypersonic Vehicle Based on Singer Model[J]. Aerospace Control， 2017， 35（4）： 62-66. （in Chinese）

[16] Farina A， Ristic B， Timmoneri L. Cramer-Rao Bound for Nonlinear Filtering with Pd<1 and Its Application to Target Tracking[J]. IEEE Transactions on Signal Processing， 2002， 50（8）： 1916-1924.

[17] Yang J L， Li P， Yang L， et al. An Improved ET-GM-PHD Filter for Multiple Closely-Spaced Extended Target Tracking[J]. International Journal of Control， Automation and Systems， 2017， 15（1）： 468-472.

[18] Kim C， Li F X， Ciptadi A， et al. Multiple Hypothesis Tracking Revisited[C]∥IEEE International Conference on Computer Vision （ICCV）， 2015： 4696-4704.

[19] Beard M， Vo B T， Vo B N. OSPA （2）： Using the OSPA Metric to Evaluate Multi-Target Tracking Performance[C]∥International Conference on Control， Automation and Information Sciences （ICCAIS）， 2017： 86-91.

Research on Multi-Target Motion Estimation Method Based on

Generalized Probability Hypothesis Density

Yu Meng1， Xu Yanke2， 3， Hu Jiaqian1*

（1. College of Astronautics， Nanjing University of Aeronautics and Astronautics， Nanjing 210016， China;

2. China Airborne Missile Academy， Luoyang 471009， China;

3. Aviation Key Laboratory of Science and Technology on Airborne Guided Weapons， Luoyang 471009， China）

Abstract： Aiming at the development needs of air-to-air operations， this paper proposes a multi-target motion estimation method based on generalized probability hypothesis density. Multi-scale analysis is introduced into based on the Faster-RCNN algorithm， and the improved K-means method is used to perform coarse clustering on the observed targets. With this as a pre-input， a probability hypothesis density filter based on generalized poisson distribution is proposed， and the clustering information is included in the weight update of the filter estimate to enhance the tracking timeliness of targets for the variable group. The simulation results show that the proposed method can still complete the recognition and classification of multiple targets without prior knowledge of the initial clustering information， and is superior to present swarm target motion estimation method in precision.

Key words： multi-target motion estimation; K-means clustering; target recognition; probability hypothesis density; situational awareness