甄绪 刘方 夏玉萍

摘 要： 传统的航迹融合算法未充分考虑传感器精度和量测丢失对航迹质量的影响， 从而导致融合后的航迹质量下降。 为了提高跟踪性能， 提出一种基于信息质量选择的动态航迹融合算法。 该算法通过交互式多模型补偿滤波来获得局部航迹和信息熵， 然后利用信息熵来度量局部航迹质量。 根据设置的双门限筛选出质量好的局部航迹， 并将其信息熵归一化的结果赋给传感器的权值， 实现权值的动态分配。 仿真结果表明， 在考虑不同的传感器精度和量测丢失率的情况下， 该算法对机动目标的跟踪性能优于已知的航迹融合算法。

关键词：多传感器; 量测丢失; 信息熵; 航迹选择; 航迹融合; 目标跟踪

中图分类号：TJ765; TP391   文献标识码：    A  文章编号：1673-5048（2021）04-0030-07

0 引  言

机动目标跟踪领域的研究工作大都假设量测数据完备， 但在实际应用中， 由于传感器本身故障、 外来干扰等一些不确定因素的影响， 导致传感器获得的信息为不完备信息[1]。 近年来， 国内外一些学者针对不完备信息， 尤其是量测丢失情况下的传感器融合估计问题进行了研究， 并取得一定的成果。 文献[2-6]基于不同的方法对滤波器进行设计改良， 研究了量测丢失情况下的系统的滤波问题，  这些方法主要针对单传感器开展研究。 文献[7-10]研究一类离散随机系统在量测丢失情况下的多传感器系统的最优估计问题， 采用的方法是集中式融合估计， 这些方法过程复杂， 计算量大， 制约了算法的工程应用。 文献[11-15]研究了量测丢失情况下的分布式多传感器系统的最优估计问题， 由于基于运动的模型单一， 方法对模型匹配要求较高， 当模型匹配不准确时， 融合估计效果变差， 不适合机动目标跟踪。 文献[16-17]从多传感器不同精度和不同量测丢失率方面对机动目标跟踪进行研究， 提高了分布式多传感器系统对机动目标的跟踪性能。 目前大部分学者都是在单一条件下对传感器的跟踪性能开展研究， 然而在实际应用中， 分布式多传感器融合系统受到干扰或发生故障时， 传感器的精度发生变化以及量测丢失等情况是同时存在的。 此外， 这些分布式多传感器融合估计方法均未充分考虑到单个传感器航迹质量的好坏对融合后的系统航迹质量的影响。

针对上述问题， 本文从航迹选择的角度出发进行研究， 提出基于信息质量选择的动态航迹融合算法。 本文算法用文献[11]中的局部最优线性滤波器代替交互式多模型中的卡尔曼滤波器， 来获取局部航迹和信息熵， 利用信息熵选择出质量好的局部航迹进行航迹融合。 该算法克服了文献[11]当模型匹配不准确时， 算法的跟踪性能变差的缺陷， 而且通过航迹选择， 避免了文献[16]及其他传统方法中质量差的航迹对系统航迹的影响， 提高了在传感器不同精度和不同量测丢失率情况下对机动目标的跟踪性能。

1 问题描述

假设量测丢失情况下的线性离散信号模型和观测模型分别为

X（t+1）=X（t）+Γw（t）（1）

Z（t）=α（t）HX（t）+v（t） （2）

式中： X（t）为t时刻的系统的状态矢量; Φ 为预测状态转移矩阵; Γ 为系统扰动矩阵; 系统扰动噪声w（t）

是均值为零、 方差为Q（t）的高斯白噪声序列; Z（t）为t时刻传感器对目标的观测值; H为观测矩阵; 观测噪声v

（t）是均值为零、 方差为R（t）的高斯白噪声序列， 且

w（t），  v（t）相互独立， 即满足：

E[w（t）]=0，

E[w（t）·wT（l）]=Q（t）δtl，

E[v（t）]=0，

E[v（t）vT（l）]=R（t）·δtl，

E[w（t）vT（l）]=0， l=1，  2，  …， t;  α（t）是取值為0或者1的离散随机变量， α（t）=1表示传感器量测到完备的数据信号， α（t）=0表示量测数据信号丢失;  λ表示传感器的数据量测丢失率， 满足Prob{α（t）=0}=λ， 0≤λ≤1， 式中α（t）=0对应δ取极限形式， 即δ→∞。

2 基于信息质量选择的动态航迹融合算法

2.1 分布式航迹融合处理流程

该算法首先通过交互式多模型（Interactive Multiple Model，  IMM）补偿滤波获得各个传感器的局部航迹和信息熵， 利用信息熵对局部航迹质量进行度量， 依据设置的信息熵双门限， 选择出质量好的局部航迹。 然后将选中的局部航迹的信息熵进行归一化处理， 将归一化的结果分配给相应的局部航迹作为融合权值， 实现权值的动态分配。 最后采用加权融合方法， 获得系统航迹信息。 图1为分布式航迹融合处理流程。

2.2 分布式航迹融合具体步骤

从图1中可以看出该航迹融合处理流程分为4个步骤， 即基于信息熵的航迹质量度量、 双门限航迹选择、 权值动态分配和航迹融合。

2.2.1 基于信息熵的航迹质量度量

（1） 交互式多模型补偿滤波

文献[11]的局部最优线性滤波器是一种类卡尔曼滤波器， 对存在量测丢失情况的信号具有很好的预测补偿作用， 但其融合算法过于复杂， 不利于工程应用。 本文将该滤波器应用到交互式多模型滤波算法中， 在模型j下的离散线性信号模型和观测模型为

xj（t+1）=Φjxj（t）+Γjwj（t）（3）

zj（t）=Hjxj（t）+vj（t） （4）

yj（t）=αj（t）zj（t）+（1-αj（t））zj（tt-1） （5）

式中： j=1， 2， …， M，  M为模型数量;  xj（t）为传感器在t时刻的系统状态矢量; 系统扰动噪声wj（t）和量测噪声vj（t）是均值为零的高斯白噪声序列， 且wj（t）， vj（t）相互独立。 αj（t）为取值为0或1的离散随机变量; zj（tt-1）为传感器从t-1到t时刻的预测的观测值; zj（t）为传感器在t时刻的真实观测值; yj（t）为本文交互式多模型补偿滤波算法所定义的传感器在t时刻的观测值， 主要用于补偿滤波， 即若t时刻存在量测丢失时， yj（t）为预测的观测值， 若t时刻不存在量测丢失时， yj（t）为真实的观测值。

通过交互式多模型算法[18]进行补偿滤波， 可以得到t时刻传感器局部航迹总体估计值为X^（tt）， 在模型j下的状态矢量估计值、 误差协方差矩阵和新息分别为x^j（tt）、 Pj（tt）和dj（t）， 与模型j最匹配的极大似然函数为Λj（t）：

x^j（tt）=x^j（tt-1）+Kj（t）[yj（t）-Hjx^j（tt-1）]（6）

Pj（tt）=[In-αjKj（t）Hj]Pj（tt-1）（7）

Λj（t）=12π|Sj（t）|exp{-12dTj（t）S-1j（t）dj（t）}（8）

则可以得到模型j的匹配概率为

uj（t）=1cΛj（t）∑Mi=1pijui（t-1）（9）

其中， 式（6）～（7）来源于文献[11] 中局部最优线性滤波器算法， 此濾波器应用于交互式多模型算法中， 通过该滤波器获得传感器的局部航迹信息。

（2）局部航迹信息熵

根据信息熵的定义， 自信息量I（X）的数学期望Hs（X）为

Hs（X） = E[I（x）] =∑x∈Xp（x）I（x） =-

∑x∈Xp（x）lgp（x）（10）

式中： Hs（X）为集合X的信息熵; p（x）为集合X中x事件发生的概率。

由信息熵的定义， 可得交互式多模型补偿滤波算法中t时刻产生的局部航迹信息熵为

Hs（X^（t|t））=∑Mj=1-uj（t）lguj（t）（11）

将Hs（X^（t|t））简写为Hs（t）。

信息熵是对系统自身不确定性的度量， 表示信息的可信程度， 一个系统越稳定， 即变量的不确定性越小， 熵值也就越小。 在交互式多模型滤波算法中， 当t时刻的量测信息为不完备信息时， 模型j产生的新息dj（t）为真实观测值与模型j在t时刻预测的观测值之差。 而模型匹配概率与新息dj（t）相关， 从而导致t时刻各个模型与目标真实运动模型的匹配误差增加， 出现模型匹配混乱现象， 即模型匹配的不确定性变大， 此时得到的各个模型的匹配概率差别较小， 该算法获得的目标状态矢量与真实值相差较大， 计算得到的信息熵较大; 相反， 当t时刻的量测信息为完备信息时， 就存在某个模型与目标真实运动模型匹配效果较好。 该算法获得的目标状态矢量与真实值相差较小， 此时计算得到的信息熵较小。

因此， 可以利用信息熵来度量局部航迹质量， 即当信息熵越小时， 该局部航迹质量就越好; 信息熵越大时， 该局部航迹质量就越差。

2.2.2 航迹选择

大量实践应用表明， 当传感器的数量大于等于2个且产生的局部航迹质量较优时， 融合产生的系统航迹具有较好的航迹质量; 然而当传感器的局部航迹质量参差不齐时， 盲目的选择所有的局部航迹进行融合， 将会降低系统航迹的质量。 在传感器不同精度及不完备量测情况下， 为了提升系统航迹质量， 需要判断局部航迹是否符合融合要求， 是选择全部航迹还是择优选择部分航迹， 为此设计一种双门限选择策略。 航迹选择流程， 如图2所示。

假设通过交互式多模型滤波算法获得传感器i的局部航迹， 其中模型k被选择的概率为uik（t）， 当uik（t）大于β时（β为模型选择概率）， 认为该时刻模型k的匹配效果较好。 β取值范围为0.7～0.9， 此时算法性能较好， 且β值的变化对算法的性能影响不大， 这一结论将在仿真环节中得到证实。 则该时刻传感器i的局部航迹信息熵为

Hsi（t）=-uik（t）lguik（t）-∑Mj=1， j≠kuij（t）lguij（t）（12）

在∑Mj=1uij（t）=1和β≤uik（t）≤1约束条件下， 可得Hsi（t）的取值范围为0～γ1（t）， 即当Hsi（t）≤γ1（t）时， 则选中该局部航迹。 此时传感器i的局部航迹的运动模型匹配效果较好， 通过该模型获得的目标运动状态矢量与目标真实值相近。

当t时刻所有的局部航迹的信息熵都大于γ1（t）时， 则按照门限γ2（t）进行航迹选择， γ2（t）定义为所有传感器局部航迹信息熵的平均值， 即

γ2（t）=∑Ni=1Hsi（t）N（13）

当Hsi（t）≤γ2（t）时， 该局部航迹被选中， 此时选中的局部航迹较其他未选中的局部航迹具有较好的航迹质量。

该算法设置了两个门限γ1（t）和γ2（t）， 其中γ1（t）<γ2（t）。 β值的设置影响门限γ1（t）， 但不受量测丢失率λ的影响。 量测丢失率λ影响局部航迹信息熵Hsi（t）， 当λ不同时， Hsi（t）也会有所不同， 该算法将会根据不同的门限进行局部航迹选择。 当量测丢失率λ较小时， 局部航迹信息熵Hsi（t）较小， 此时局部航迹质量较好， 通过γ1（t）将航迹质量较好的局部航迹选择出来; 当量测丢失率λ较大时， 局部航迹信息熵Hsi（t）较大， 此时局部航迹质量较差， 通过γ2（t）将航迹质量相对较好的局部航迹选择出来。

2.2.3 权值分配

假设被选中的传感器局部航迹数量为n， n≤N， 按照选中的先后顺序将传感器的局部航迹进行编号。 t时刻传感器i（i=1， 2， …， n）的局部航迹信息熵Hsi（t）越小， 表示传感器i的局部航迹质量越好， 该航迹在航迹融合时权值分配应该越大。 将t时刻所有被选中的传感器的局部航迹信息熵的倒数1/Hsi（t）进行归一化处理， 将其归一化的结果作为局部航迹融合时的权值， 权值wi（t）满足传感器i的局部航迹信息熵越小， 在航迹融合时权值分配越大的原则。 wi（t）的表达式为

wit=1/Hsi（t）∑ni=11/Hsi（t）（14）

∑ni=1wi（t）=1（15）

2.2.4 航迹融合

t时刻通过航迹选择获得的传感器i的局部航迹状态矢量为X^i（t|t）， 融合权值为wi（t）， 进行加权融合， 得到系统航迹X（t|t）：

X（t|t）=∑ni=1wi（t）X^i（t|t）（16）

3 仿真结果与分析

为了验证该算法的有效性， 实验中， 交互式多模型采用CV， CA， CT三种模型， 系统状态向量为X=[x x· y y· x¨ y¨]T， 模型的先验概率为U=[1/2 1/6 1/3]， 模型的转移概率矩阵为

P=0.700.150.150.150.700.150.150.150.70（17）

本次实验采用3个传感器对同一目标进行观测， 采样周期和融合周期均为1 s， 观测时长为120 s， 传感器的位置分別为（-40 km，  -5 km）、 （-20 km，  -20 km）、 （-10 km，  -10 km）， 量测方程为

Zk（t）=HX（t）+Vk（t）， k=1， 2， 3（18）

式中： Vk（t）是均值为零的高斯白噪声序列; H为观测矩阵，

H=1 0 0 0 0 00 0 1 0 0 0。

实验假定传感器的观测数据已经完成数据关联和时空校准等数据预处理环节， 比较在不同情况下文献[11]算法、 文献[16]算法和本文算法的跟踪性能。 实验采用蒙特卡洛仿真方法， 仿真次数为m=500次， 跟踪性能指标为距离均方根误差， 其表达式如下：

RMSE=∑mi=1（（x-x^i）2+（y-y^i）2）m

（19）

假设目标做机动运动， 初始位置为（-3 000 m， 1 000 m）， 初始速度445 m/s， 在0～30 s匀速飞行; 在31～60 s以转弯率为0.03 rad/s做转弯运动; 在61～90 s以转弯率为-0.03 rad/s做转弯运动; 在91～120 s以转弯率为0.03 rad/s做转弯运动。 图3为机动目标航迹。

3.1 三种算法的跟踪性能比较及β值对算法跟踪性能的影响

假设3个传感器的观测精度均为28.28 m， 量测丢失率相同， 在λ=20%和λ=50%两种情况下进行仿真实验。

图4为λ=20%时三种算法的跟踪性能比较。 从图中可以看出， 文献[11]算法虽然在部分观测时间段内的跟踪性能优于本文算法和文献[16]算法， 但是该方法需要经过很长的观测时间才能达到稳定的跟踪效果， 特别是当目标的运动状态发生转变时， 文献[11]算法表现出极大的不稳定性， 总体跟踪性能较差。 经实验分析得到， 文献[11]算法在CT和CV模型下的跟踪性能比在CA模型下的跟踪性能还要差。 而文献[16]算法虽然在跟踪机动目标时的总体性能优于文献[11]算法， 但整体性能仍然不如本文算法。

表1和图5表明， 在同一λ值情况下， 当β取值分别为0.7， 0.8和0.9时， 本文算法的RMSE曲线几乎完全重合，RMSE值也几乎相等， 算法的跟踪性能优于文献[16]算法的跟踪性能， 随着λ值变大， 本文算法的跟踪性能开始下降。

经仿真实验数据统计分析， 当β取值范围为0.7～0.9时， 门限γ1的取值范围为0.4～0.8; 当λ在0～50%之间取任意值时， 本文算法获得的各传感器局部航迹信息熵都分布在0～1.098之间。 因此， γ1的取值在各传感器局部航迹信息熵取值分布范围内， 不会远大于或远小于局部航迹信息熵可能的取值范围， 确保了本文算法中双门限航迹选择的实现。

由于实际过程中目标运动的不确定性， 算法中模型选择的不准确， 都会导致模型匹配概率不高， 因此β值不宜设置过大。 此外， 当β取值范围为0.9～1时， 门限γ1的取值范围为0～0.4， 在0～γ1区间内各传感器的局部航迹信息熵分布较少， γ1值随着β值的增大而减小， 致使大部分局部航迹通过门限γ2进行选择， 而通过门限γ1进行选择的航迹很少， 容易导致门限γ1失效， 航迹筛选效果不佳。

同理， 当β取值范围为0.5～0.7时， 门限γ1的取值范围为0.8～1.039， 在0～γ1区间内各传感器的局部航迹信息熵分布较多， γ1值随着β值的减小而增大， 致使大部分局部航迹通过门限γ1进行选择， 而通过门限γ2进行选择的航迹很少， 容易导致门限γ2失效， 航迹筛选效果不佳。 当β值小于0.5时， 此时模型匹配概率较低， 局部航迹质量较差， 因此β值设置要高于0.5。

综上， 为了确保获得较好的航迹筛选效果， 将β的取值范围设置为0.7～0.9。 此外， 当λ在0～50%之间取值， β在0.7～0.9之间取值时， β的取值对算法的跟踪性能影响不大， 本文算法跟踪性能随着λ取值的增加而降低。

3.2 文献[16]算法与本文算法的跟踪性能比较

从3个传感器的观测精度不同或量测丢失率不同等方面， 来比较文献[16]算法和本文算法对机动目标的跟踪性能， 下面的实验β取值为0.8。

3.2.1 传感器量测丢失率相同、 观测精度不同情况下的跟踪性能比较

假设3个传感器的量测丢失率相同， 均为25%， 而观测精度不相同， 分别在三种不同情况下进行比较：

情况1： 3个传感器的观测精度差别不大， 分别为28.28 m， 30.41 m， 32.53 m。

情况2： 3个传感器的观测精度差别较大， 分别为28.28 m， 31.82 m， 35.36 m。

情况3： 3个传感器的观测精度差别较大， 分别为28.28 m， 33.94 m， 39.59 m。 实验结果如表2和图6所示。

表2和图6表明， 当量测丢失率为25%， 3个传感器观测精度差别不同时， 文献[16]算法的跟踪精度相对于传感器1的跟踪精度分别提高6.63%， 3.84%， 1.32%， 本文算法的跟踪精度相对于传感器1的跟踪精度分别提高23.41%， 20.08%， 17.02%， 并且本文算法的跟踪性能优于文献[16]算法的跟踪性能， 跟踪精度分别提高17.97%， 16.87%和15.91%。

不断增加λ值， 在3个传感器观测精度差别不大的情况下， 对比单传感器跟踪与融合算法跟踪的跟踪性能， 仿真实验结果如表3所示。

从表2～3中可知， 单传感器、 文献[16]算法和本文算法的跟踪精度都会随着量测丢失率的增加而降低， 当λ<25%时， 本文算法的跟踪精度数值小于3个传感器的观测精度最小设置值， 同时小于单传感器和文献[16]算法的跟踪精度; 当λ<50%时， 本文算法的跟踪精度小于3个传感器观测精度数值的最大设置值， 仍小于单传感器和文献[16]算法的跟踪精度; 当λ>50%时， 通过仿真实验发现， 本文算法的跟踪精度数值开始大于3个传感器观测精度的最大设置值， 但跟踪性能仍然优于单传感器和文献[16]算法的跟踪性能。

因此无论λ值如何变化， 本文算法的跟踪精度始终小于单传感器和文献[16]算法， 其跟踪性能始终优于单传感器和文献[16]算法。 但考虑到当λ>50%时， 在实际应用过程中， 该传感器已经不能发挥作用， 因此对λ>50%的情况不再进行深入分析。

3.2.2 传感器观测精度相同、 量测丢失率不同情况下的跟踪性能比较

假设3个传感器观测精度相同， 均为28.28 m， 量测丢失率不同， 分为两种不同情况进行比较。

情况1： 3个传感器的量测丢失率相差不大， 分别为25%， 30%， 35%。

情况2： 3个传感器的量测丢失率相差较大，  分别为25%， 35%， 45%。

實验结果如表4和图7所示。 从表4和图7知，  当3个传感器观测精度均为28.28

m， 量测丢失率不同时， 文献[16]算法的跟踪精度相对于传感器 1的跟踪精度分别提高5.52%、 降低13.25%， 该算法的跟踪性能开始变差; 本文算法的跟踪精度相对于传感器1的跟踪精度分别提高27.32%， 24.41%， 其中传感器1在3个传感器中跟踪性能最好， 并且本文算法的跟踪性能始终优于文献[16]算法的跟踪性能。 经仿真实验验证， 当3个传感器中一个或者两个传感器的量测丢失率大于50%时， 其他传感器的量测丢失率小于50%时， 本文算法的跟踪性能仍然优于单传感器和文献[16]算法的跟踪性能。

3.2.3 传感器量测丢失率不同、 观测精度不同情况下的跟踪性能比较

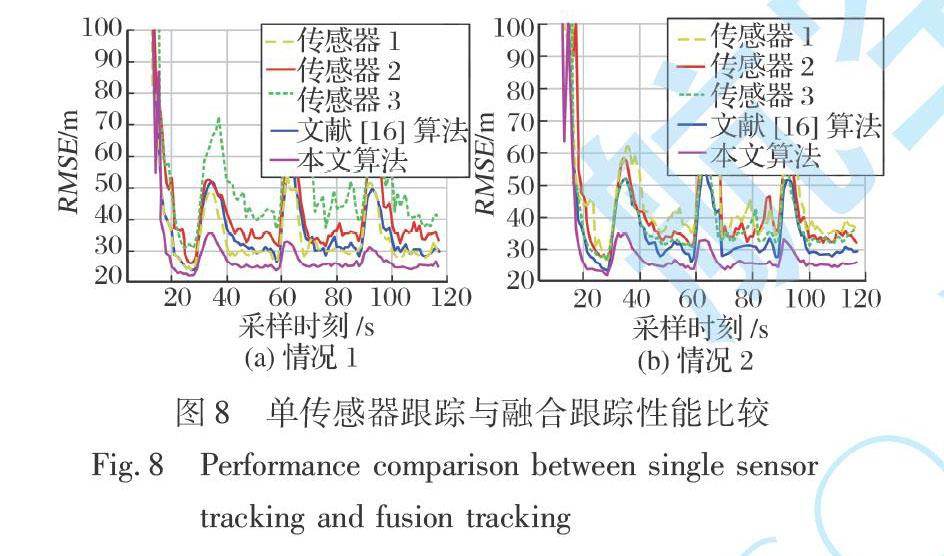
情况1： 传感器的量测丢失率随着观测精度的增大而减小。 3个传感器的观测精度分别为28.28 m， 30.41 m， 32.53 m， 量测丢失率分别为25%， 30%， 35%。

情况2： 传感器的量测丢失率随着观测精度的增大而增大。 3个传感器的观测精度分别为28.28 m， 30.41 m， 32.53 m， 量测丢失率分别为35%， 30%， 25%。

实验结果如表5和图8所示。

从表5和图8知， 当3个传感器观测精度不相同， 量测丢失率也不相同时， 文献[16]算法的跟踪精度相对于均方根误差最小的传感器1的跟踪精度分别降低2.99%、 提高22.74%， 本文算法的跟踪精度相对于传感器1的跟踪精度分别提高21.11%， 40.86%， 其中传感器1在3个传感器中跟踪性能最好。

上述仿真实验表明， 多传感器跟踪机动目标时， 当传感器间观测精度不同或丢失率不同时， 无论λ取何值时， 本文算法的跟踪性能始终优于单传感器的跟踪性能和文献[16]算法的跟踪性能。

4 结 束 语

本文引入信息熵的概念用来度量局部航迹质量， 提出一种基于信息质量选择的动态航迹融合算法。 仿真结果表明， 当分布式多传感器跟踪系统受到干扰时， 在传感器精度发生变化以及量测丢失情况下， 采用本文算法能够获得较好的跟踪性能。 运动模型选择的好坏对本文算法的应用有较大影响， 因此研究探索一种不受模型影响或受模型影响较小的算法是目前亟待解决的问题。

参考文献：

[1] Ma K，  Zhang H G，  Wang R T，  et al. Target Tracking System for Multi-Sensor Data Fusion[C]∥2017 IEEE 2nd Information Technology，  Networking，  Electronic and Automation Control Conference （ITNEC），   2017.

[2] Shi J，  Qi G Q，  Sheng A D. Tracking Filter Using Measurements of Target Extent with Intermittent Observation[C]∥2013 International Conference on Computational and Information Sciences，   2013.

[3] Yan L P，  Zhou D H，  Fu M Y，  et al. State Estimation for Asynchronous Multirate Multisensor Dynamic Systems with Missing Mea-surements[J]. IET Signal Processing，  2010，  4（6）： 728.

[4] Deng Z H，  Shi L，  Yin L J，  et al. UKF Based on Maximum Correntropy Criterion in the Presence of both Intermittent Observations and Non-Gaussian Noise[J]. IEEE Sensors Journal，  2020，  20（14）： 7766-7773.

[5] Sun S L，  Tian T，  Lin H L. Optimal Linear Estimators for Systems with Finite-Step Correlated Noises and Packet Dropout Compensations[J]. IEEE Transactions on Signal Processing，  2016，  64（21）： 5672-5681.

[6] Ma J，  Sun S L. Linear Estimators for Networked Systems with One-Step Random Delay and Multiple Packet Dropouts Based on Prediction Compensation[J]. IET Signal Processing，  2017，  11（2）： 197-204.

[7] Korany Mohamed S M，  Nahavandi S. Optimal Multisensor Data Fusion for Linear Systems with Missing Measurements[C]∥2008 IEEE International Conference on System of Systems Engineering，  2008： 1-4.

[8] Yang C，  Zheng J Y，  Ren X Q，  et al. Multi-Sensor Kalman Filtering with Intermittent Measurements[J]. IEEE Transactions on Automatic Control，  2018，  63（3）： 797-804.

[9] Qi B，  Sun S L. Optimal Filtering of Multi-Sensor Networked Systems with Unknown Channel Interferences and Compensation of Packet Losses[C]∥36th Chinese Control Conference （CCC），  2017.

[10] Shivashankarappa N，  Raol   J R. Data Fusion Algorithms with State Delay and Missing Measurements[J]. International Journal of Engineering Research and Applications，  2017，  7（6）： 62-68.

[11] Ding J，  Sun S L，  Ma J，  et al. Fusion Estimation for Multi-Sensor Networked Systems with Packet Loss Compensation[J]. Information Fusion，  2019，  45： 138-149.

[12] 許志刚，  盛安冬，  郭治. 基于不完全量测下离散线性滤波的修正Riccati方程[J]. 控制理论与应用，  2009，  26（6）： 673-677.

Xu Zhigang，  Sheng Andong，  Guo Zhi. The Modified Riccati Equation for Discrete-Time Linear Filtering with Incomplete Mea-surements[J]. Control Theory & Applications，  2009，  26（6）： 673-677.（in Chinese）

[13] 吴黎明，  马静，  孙书利. 具有不同观测丢失率多传感器随机不确定系统的加权观测融合估计[J]. 控制理论与应用，  2014，  31（2）： 244-249.

Wu Liming，  Ma Jing，  Sun Shuli. Weighted Measurement Fusion Estimation for Stochastic Uncertain Systems with Multiple Sensors of Different Missing Measurement Rates[J]. Control Theory & Applications，  2014，  31（2）： 244-249.（in Chinese）

[14] 楚天鹏. 不完全信息下分布式目标跟踪算法[J]. 兵工自动化，  2017，  36（9）： 39-44.

Chu Tianpeng. Distributed Target Tracking Algorithm with Incomplete Information[J]. Ordnance Industry Automation，  2017，  36（9）： 39-44.（in Chinese）

[15] Chen B，  Zhang W A，  Yu L. Distributed Fusion Estimation with Missing Measurements，  Random Transmission Delays and Packet Dropouts[J]. IEEE Transactions on Automatic Control，  2014，  59（7）： 1961-1967.

[16] 李松，  胡振濤，  李晶，  等. 基于多传感器不完全量测下的机动目标跟踪算法[J]. 计算机科学，  2013，  40（8）： 277-281.

Li Song，  Hu Zhentao，  Li Jing，  et al. Multi-Sensor Information Fusion Motivate Target Tracking Algorithm Based on Missing Measurements[J]. Computer Science，  2013，  40（8）： 277-281.（in Chinese）

[17] Zhang K，  Wang Z Y，  Guo L L，  et al. An Asynchronous Data Fusion Algorithm for Target Detection Based on Multi-Sensor Networks[J]. IEEE Access，  2020（99）： 1.

[18] Mazor E，  Averbuch A，  Bar-Shalom Y，  et al. Interacting Multiple Model Methods in Target Tracking： A Survey[J]. IEEE Transactions on Aerospace and Electronic Systems，  1998，  34（1）： 103-123.

Dynamic Track Fusion Algorithm Based on

Information Quality Selection

Zhen Xu， Liu Fang ， Xia Yuping

（National Key Laboratory of Science and Technology on Automatic Target Recognition，

National Defense Science and Technology University，   Changsha 410005，  China）

Abstract： The traditional track fusion algorithm does not fully consider the situation that the accuracy of sensors and the measurement loss lead to the track quality degradation. In order to improve the performance of dynamic tracking，  a dynamic track fusion algorithm based on information quality selection is proposed. The algorithm obtains the local track and information entropy by interacting multiple model compensation filtering，  and then uses the information entropy to measure the quality of the local track. The local track with good quality is selected according to the double threshold. Then，   the information entropy normalization result is assigned to the weight of the sensor to realize the dynamic matching of the weight. The simulation results show that the algorithm outperforms the known track fusion algorithm in tracking maneuvering targets with different sensor accuracy  and measurement losses.

Key words： multi sensor; measurement loss; information entropy; track selection; track fusions;  target tracking