何黎霞， 孙峪怀， 胡 艳

(四川师范大学 数学科学学院， 四川 成都 610066)

0 引言

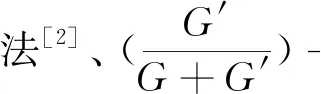
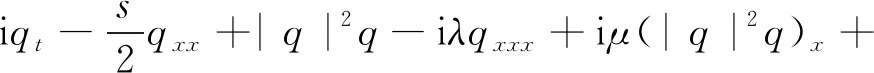
(1)

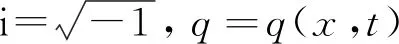
1 方法的简述

完全判别系统法的主要步骤可概括如下：

考虑非线性数学和物理方程

P(q,qx,qt,qxx,qxt,qtt,…)=0,

(2)

其中,q=q(x,t)是未知函数，P是关于q及其偏导数的多项式.作行波变换q(x,t)=u(ξ)exp(iφ),ξ=x-ct,φ=x+ωt+θ，方程(2)简化为如下常微分方程

u′(ξ)=F(u,a1,…,am),

其中,a1,…，am是参数.将上式积分一次，得到

(3)

其中,ξ0是积分常数.显然，只需求解(3)式.然而, 确定参数a1,…,am的取值范围却十分困难.借助多项式的完全判别系统[16]，确定参数a1，…，am的取值范围，从而得到F(u,a1,…,am)的具体形式.最后，直接求解积分式(3)，进而得到方程(1)的解.

2 过程与结果

假设方程(1)有如下形式的解

q(x,t)=u(ξ)exp(iφ),ξ=x-ct,φ=x+ωt+θ,

(4)

其中,u和φ分别表示q的振幅和相位.将(4)式代入方程(1)，并且令虚部和实部分别为零，可得

(5)

(6λ-s)u″=(2ω+2λ-s)u+(2μ-2)u3,

(6)

比较方程(5)和方程(6)，有

对方程(5)积分一次，可得

(u′)2=mu4+nu2+a2,

(7)

其中,a2是积分常数，

作如下变换

方程(7)转化为

(8)

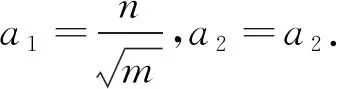
将方程(8)写成积分形式，有

(9)

其中,ζ0是积分常数，并且在方程(1)的精确解中令其为零.

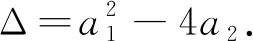
情形1假设Δ=0.由于ψ>0，有

(10)

如果a1<0，由(10)式可得方程(1)有如下形式的解

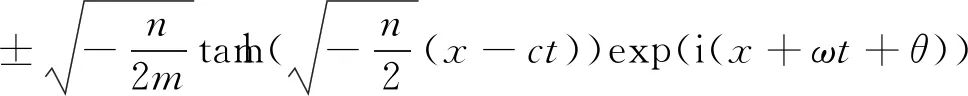
其中,

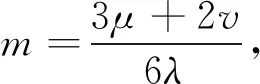
如果a1>0，由(10)式可得方程(1)有如下形式的解

其中,

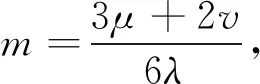
如果a1=0，由(10)式可得方程(1)有如下形式的解

其中,

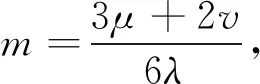
情形2假设Δ>0并且a2=0.由于ψ>-a1，有

(11)

如果a1<0，由(11)式可得方程(1)有如下形式的解

其中,

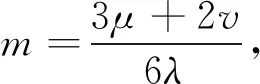
如果a1>0，由(11)式可得方程(1)有如下形式的解

其中,

情形3假设Δ>0，a2≠0并且α<β<γ.假设α,β,γ中一个为零，其余为F(ψ)的根.作变换ψ=α+(β-α)sin2φ，可得

(12)

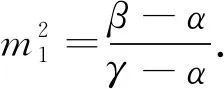
其中,

当m1=0或m1=1时，Jacobi椭圆函数将退化为三角函数或双曲函数，从而得到方程(1)额外的解

其中,

当m1=0或m1=1时,Jacobi椭圆函数将退化为三角函数或双曲函数，从而得到方程(1)额外的解

其中,

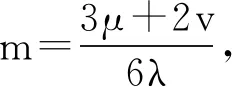
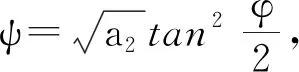
(13)

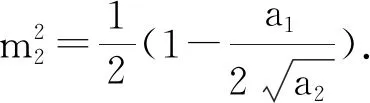
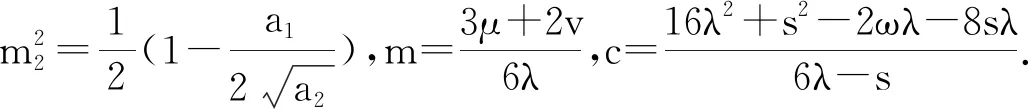
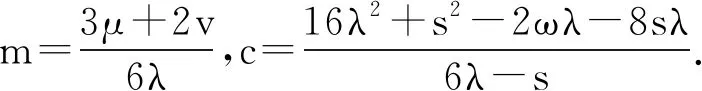
为了更直观地理解这些显示解，将参数取特殊值，绘制了部分显示解的三维图.图1(a)-图3(a)分别表示扭结波解q1(x,t)、周期波解q15(x,t)以及暗孤波解q16(x,t).图1(b)-图3(b)分别表示三个行波解在t=0，t=1时沿x轴的波.

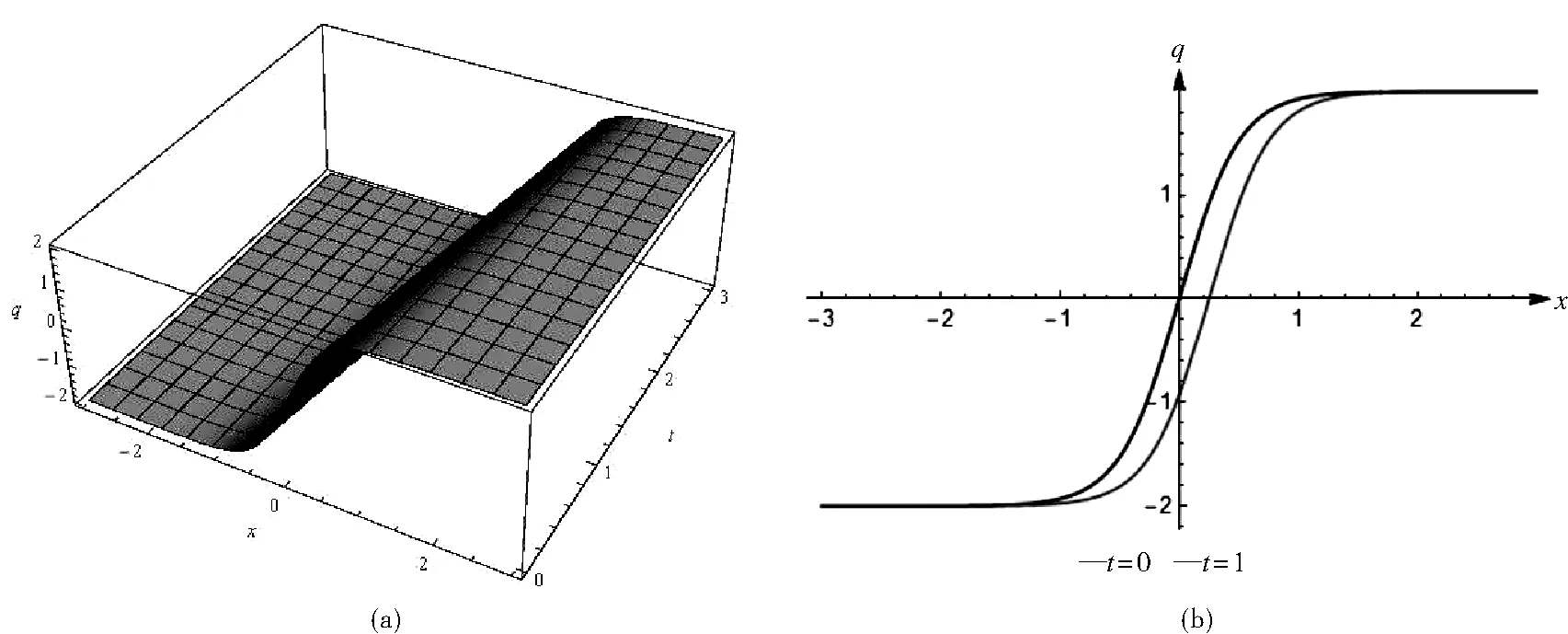
图1 扭结波解q1(x,t),当时的图像

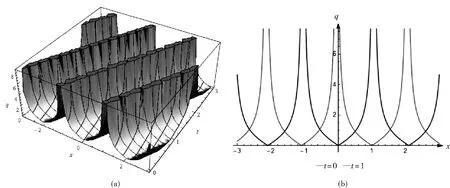
图2 周期波解q15(x,t),当时的图像

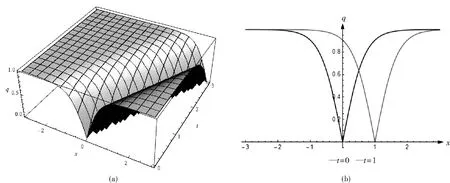
图3 暗孤波解q16(x,t),当时的图像

3 结论