王建红

（上海立信会计金融学院 统计与数学学院，上海201209）

0 引言

行列式是线性代数课程中的一个基本概念，也是解决一些数学问题的重要工具。行列式的出现源于线性方程组的求解，是由德国数学家莱布尼茨和日本数学家关孝和发明的。后来，瑞士数学家克莱姆对行列式的定义和展开法则作出了比较完整、明确的阐述，并给出了现在所称的解线性方程组的克莱姆法则[1，2]。行列式在数学分析、几何学、运筹学、线性方程组理论和二次型理论等多方面有着重要的应用。除了数学学科上的应用之外，其在物理学、力学、天文学以及其他技术学科中也有广泛应用[3，4]。行列式的理论奠定了高等数学的理论基础，同时也为数学在现实生活中的广泛运用提供了理论依据，因此行列式的计算是线性代数教学中的重要内容之一。其计算方法较多，技巧性较强。要想掌握好行列式的计算，首先需具体分析所求行列式的特点和元素的规律性，针对其特征采取适当的方法。其次，通过做题不断总结，积累经验。本文通过分析一些具体行列式的结构特点，介绍了常见的9种计算具体行列式的方法，给出了一些计算抽象型行列式的技巧。

1 具体型行列式的计算方法

1.1 定义法

定义：

其中p1,p2…p n是n阶排列。

由行列式定义可知，其展开是n!项之和，因此定义法基本只适合低阶（二或三阶）行列式和非零元素特别少的行列式（一般不多于2n个）。对于有些零元素分布比较有规律，如上（下）三角形行列式和含有零块的行列式，也可以考虑利用定义法计算。由于定义法不太常用，这里不举例说明。

1.2 化三角形法

性质：

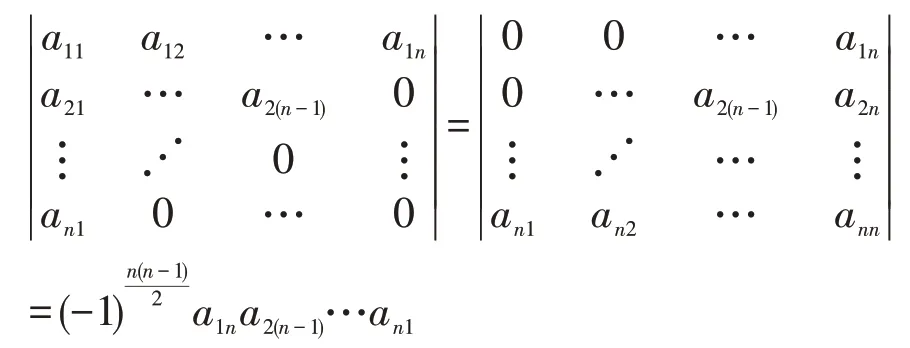
该性质中的行列式分别称为主对角线和次对角线的上（下）三角行列式。一般地，行列式自身不一定满足此形式，可利用行列式的性质将其化为该形式。化三角形法是行列式计算中最常用的方法,特别适合于一类爪型（或可化为爪型）行列式以及行和（列和）相等的行列式计算。所谓爪型行列式是指除首行首列和主对角线元素外其余元素均为零的行列式。

解法一：各行元素之和相等，将所有列加至第一列，再化为上三角行列式。

解法二：可将各行减去第1行，化为爪型行列式，再化为上三角行列式。

1.3 降阶法

利用行列式按行（列）展开定理或拉普拉斯定理将其降成低阶行列式计算。按行（列）展开前一般需要利用行列式的性质将某行（列）化为只有一个非零元素的行（列）。若行列式中出现大片的零元素，即包含零块，且非零的k阶子式个数较少时，也可利用拉普拉斯定理将行列式较快的降阶。

解：该行列式第二行是同一元素，其余各行与第二行有(n-1)个元素相同，因此将其余各行减去第二行，将第一行化成只有一个非零元素，再按第一行展开降阶可得

1.4 增阶法

增阶法是指在不改变原行列式值的情况下，通过增加一特殊行和列对行列式进行计算。该方法一般适合于行列式中每行或每列对应位置元素（除对角线位置外）都相同的。增加的行和列，一般需要首行首列元素为1,首行其余元素为每行相同的元素，首列其余元素均为零。增加一阶后一般可利用行列式的性质化为爪型行列式再计算。

解：通过增加一行和一列可得

1.5 拆项法

当行列式某行（列）是两项或多项之和时，可利用行列式的性质将其拆成两个或多个行列式的和再计算。但有些行列式不具备这种形式时，也可以用拆项法简化计算，将某行（列）所有元素拆成两项之和，有些项看成加上零元素。

解：1.若b=c，由例1可知

D n=[a+(n-1)b](a-b)(n-1)。

2.若b≠c，将最后一列中b=b+0,a=b+(a-b),得

由于b,c是对称的，则

1.6 数学归纳法

数学归纳法一般适合于行列式的结论已知且结论与自然数相关，尤其是关于行列式的证明题。也可以用于在计算n阶行列式时，先计算n=1,2的情形，找出一般规律，归纳出n阶的结论，再用数学归纳法给出证明。

例5.计算

解：易 知n=1,D1=cosθ；n=2,D2=2 cos2θ-1=cos 2θ因此猜想D n=cosnθ。

这时可以利用数学归纳法给出证明,n=1时，显然成立。假设结论≤n-1阶成立，则将D n按最后一行展开可得

Dn=2 cosθD n-1-D n-2=2 cosθcos(n-1)θ-cos(n-2)θ=cosnθ。

1.7 递推公式法

若行列式的元素分布比较有规律，可以设法找出n阶行列式与较低阶行列式之间的递推关系式，再解出此行列式。一般递推关系式有以下两种情形:

（1）若n阶行列式满足aD n+bD n-1+c=0，需再找出D n与D n-1的另一个关系式，联立方程组解出D n;

（2）若n阶行列式满足aD n+bD n-1+cD n-2=0，则考虑特征方程ax2+bx+c=0。

1.若特征方程的判别式Δ≠0，则特征方程有两个不相等的根x1,x2，此时可设(A,B待定)，令n=1,n=2解出A,B即可。

2.若特征方程的判别式Δ=0，则特征方程有两个相等的根x1、x2，此时可设(A,B待定)，同样令n=1,n=2解出A,B即可。

例6.计算

解：将此行列式按第一列展开可得

所以，特征方程为x2-2ax+a2=0，有两个相等的特征根x1=x2=a。

可设D n=(A+nB)an-1，又因为

所以D n=(n+1)an。

1.8 公式法

公式法一般是指利用范德蒙行列式的计算结果来计算某些可化为该形式的行列式。n阶范德蒙行列式为：

V n=0⇔x i(i=1,2，…，n)中至少两个相等。

例7.计算

解：将第一行1=ai-(a i-1)，则该行列式可化为两个范德蒙行列式

1.9 特征值法

设是n阶矩阵A的全部特征值（重根按重数计算），则矩阵A的行列式|A|=λ1λ2…λn。所谓矩阵A的特征值λi是指满足方程 |λi E-A|=0的根。由于计算特征值时需要求行列式，所以用特征值法计算行列式的方法不常用，一般可用于一些证明题中。

2 抽象型行列式的计算技巧

抽象型行列式是指不给出具体元素，往往涉及与行列式相关联的方阵、伴随阵、逆矩阵、分块矩阵或用行（列）向量表示的矩阵等行列式的计算。因此，计算此类行列式需灵活运用矩阵和行列式的有关性质。

（1）设A是n阶方阵，k是一常数，则|AT|= |A|, |kA|=k n|A|，|A*|= |A|n-1（A*是A的伴随矩阵）

（2）若A是n阶可逆方阵，则 ||A-1= ||A-1。

（3）设A,B均是n阶方阵，则 ||AB= ||A||B。

（4）设A,B分别是m阶和n阶方阵，对于分块矩阵，其行列式

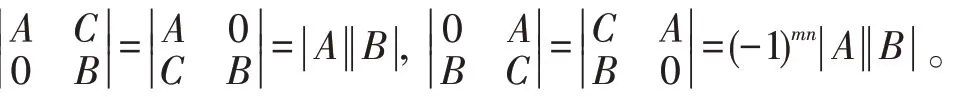
（5）若A是n阶可逆方阵，对于分块矩阵，利用初等变换可得，两边取行列式得

（6）若行列式的行或列以向量及其运算形式给出时，可利用行列式的性质计算。