常娟，杜迎雪，刘卫锋

（郑州航空工业管理学院数学学院，河南郑州 450046）

0 引言

作为经典Zadeh 模糊集［1］的重要推广，直觉模糊集（intuitionistic fuzzy set，IFS）［2］用隶属度和非隶属度分别表示肯定和否定的程度，能更全面地描述模糊信息。IFS 要求隶属度和非隶属度之和不大于1，但在决策过程中，往往会出现二者之和大于1 的情况，此时IFS 的决策理论和方法就不再适用。为此，YAGER 等［3-4］在IFS 补运算的基础上，将隶属度和非隶属度的取值范围由三角形区域（μ+ν≤1）拓展至14 圆区域（μ2+ν2≤1），由此提出毕达哥拉斯模糊集（Pythagorean fuzzy set，PFS）。显然，PFS延续了IFS 的优势，应用范围更广泛。近年来，PFS已成为研究热点，并取得了丰富的研究成果。其中，ZHANG 等［5-6］给出了PFS 的定义，并定义了毕达哥拉斯模糊集（Pythagorean fuzzy number，PFN）的运算和距离、相似度和比较方法；PENG 等［7］定义了PFN 的除法和减法运算；李德清等［8］比较分析了PFN 的排序方法，并重新定义了PFN 的距离；曾守桢等［9］提出了PFS 的混合加权距离测度。在决策方法方面，文献［5，8-9］基于不同的距离测度将逼近理想解排序法（technique for order preference by similarity to an ideal solution，TOPSIS）应用于PFN环境；REN 等［10］研究了在毕达哥拉斯模糊环境下的TODIM 多属性决策方法；杨艺等［11］将偏好关系引入PFN，并将其用于群决策问题。在集成算子方面，刘卫锋等［12-13］定义了PFN 加权平均算子和加权几何算子、拟有序加权算子、交叉影响算子等一系列算子；WU 等［14］、彭定洪等［15］分别提出了毕达哥拉斯模糊Hamacher 算子和Heronian 算子。以上研究是毕达哥拉斯模糊理论的重要内容，也为处理不同条件下的决策问题提供了方法。

虽然PFS 克服了直觉模糊集的不足，但并不能刻画决策者在决策时犹豫不决的状态，为此，结合TORRA［16］定义的犹豫模糊集，刘卫锋等［17］定义了毕达哥拉斯犹豫模糊集（Pythagorean hesitation fuzzy set，PHFS）。PHFS 既能刻画决策者现实的犹豫状况，又扩充了隶属度和非隶属度的范围，因此在决策理论和实际应用中具有重要意义。最近，关于PHFS 的研究取得了一些新成果，刘卫锋等［17-18］提出了毕达哥拉斯犹豫模糊数（Pythagorean hesitation fuzzy number，PHFN），并定义了PHFN 的运算、比较方法、加权集成算子和相关测度；WEI 等［19-21］研究了毕达哥拉斯犹豫模糊Hamacher 集成算子、Hamy 平均算子和Bonferroni 平均算子；LIANG等［22］研究了毕达哥拉斯犹豫模糊TOPSIS 法；此外，KHAN 等［23］也提出了PHFS，但其本质为IFS 在毕达哥拉斯模糊环境中的推广，与刘卫锋等［17］提出的PHFS 不全相同。可见，PHFS 的理论成果已日趋丰富，但以上成果偏重于集成算子理论，涉及距离测度研究的文献较少，文献［22］仅研究了PHFN 的距离，并未涉及PHFS 的距离测度，而距离测度是反映模糊集间差异程度的重要工具，有重要的理论价值，因此，关于PHFS 的距离测度研究，特别是涉及元素权重和位置权重的距离测度研究是非常必要的。

受文献［9，24-25］启发，本文从有序加权角度研究PHFS 的距离测度，同时在兼顾属性权重的基础上，定义广义PHFS 混合加权距离测度（DGPHFHWA），研究其特殊形式和性质。此外，针对属性值为PHFN 且权重未知的多属性决策问题，通过指数熵确定属性权重，并提出基于DGPHFHWA的多属性决策方法。最后，通过算例及方法对比说明本文方法的可行性和合理性。

1 相关概念

根据YAGER 等［3-4］提出的PFS 隶属度的特点，ZHANG 等［5］给出PFS 的定义。

2 广义PHFS 混合加权距离测度

为定义2 个PHFS 的距离测度，首先定义PHFN 的距离，设α=。一般情况下集合的基数是不相等的，即|，为确保计算的合理性，以上集合应具有相同的基数。针对此问题，考虑决策者不同的风险偏好，XU 等［26］提出，拓展基数小的集合，通过添加元素使2 个集合的基数相等，具体为：

（1）乐观角度，在基数小的集合中添加多个大元素；

（2）悲观角度，在基数小的集合中添加多个小元素。

通过以上处理，给出以下犹豫模糊集的距离测度。

3 基于DGPHFHWA的PHF 决策方法

在多属性决策问题中，当邀请多位专家确定隶属度和非隶属度信息时，决策数据往往难以达成一致，而且容易出现最大隶属度和非隶属度之和大于1 的情况。针对此问题，用PHFN 表示属性值，既可以扩充隶属度和非隶属度的范围，又可以完整体现决策数据，避免信息丢失。因此，研究属性值为PHFN 的多属性决策问题具有实际意义。

4 决策应用

4.1 决策算例

例1近年来，随着我国移动设备的普及和信息技术的快速发展，电子商务得到了迅猛发展，我国已成为全球电子商务的引领者。物流作为实现电子商务的重要环节，不仅承担着大部分成本，也是实体商品和客户之间最直接的沟通环节，因此电子商务的成败与物流质量密不可分。设某电子商务公司因业务发展，需要选择合适的物流公司，现有4 个物流公司｛A1，A2，A3，A4｝可供选择。通过邀请相关领域的专家，从经营状况（e1）、信息化水平（e2）、设备设施（e3）、管理与服务（e4）4 个指标对各物流公司进行评估。各物流公司在各指标下的评估信息用PHFN表示。例如：每位专家分别用［0，1］间的数字评估对公司A1经营状况（e1）的满意度和不满意度，满意度分值越高表示越满意，不满意度分值越高表示越不满意。因为不同的专家意见可能不一致，最终评定满意度为0.3 和0.8，不满意度为0.4。故A1在属性指标e1下的评估值用PHFNα11=表示。类似地，可确定其他指标值αij，i=1，2，3，4，j=1，2，3，4，具体如表1 所示。

表1 毕达哥拉斯犹豫模糊决策矩阵Table 1 Pythagorean hesitant fuzzy decision matrix

步骤1由于各指标值均属于效益型，故不需要对决策矩阵进行规范化处理。由定义11，计算各属性信息的指数熵，得

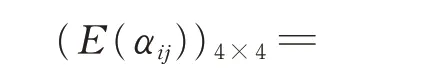
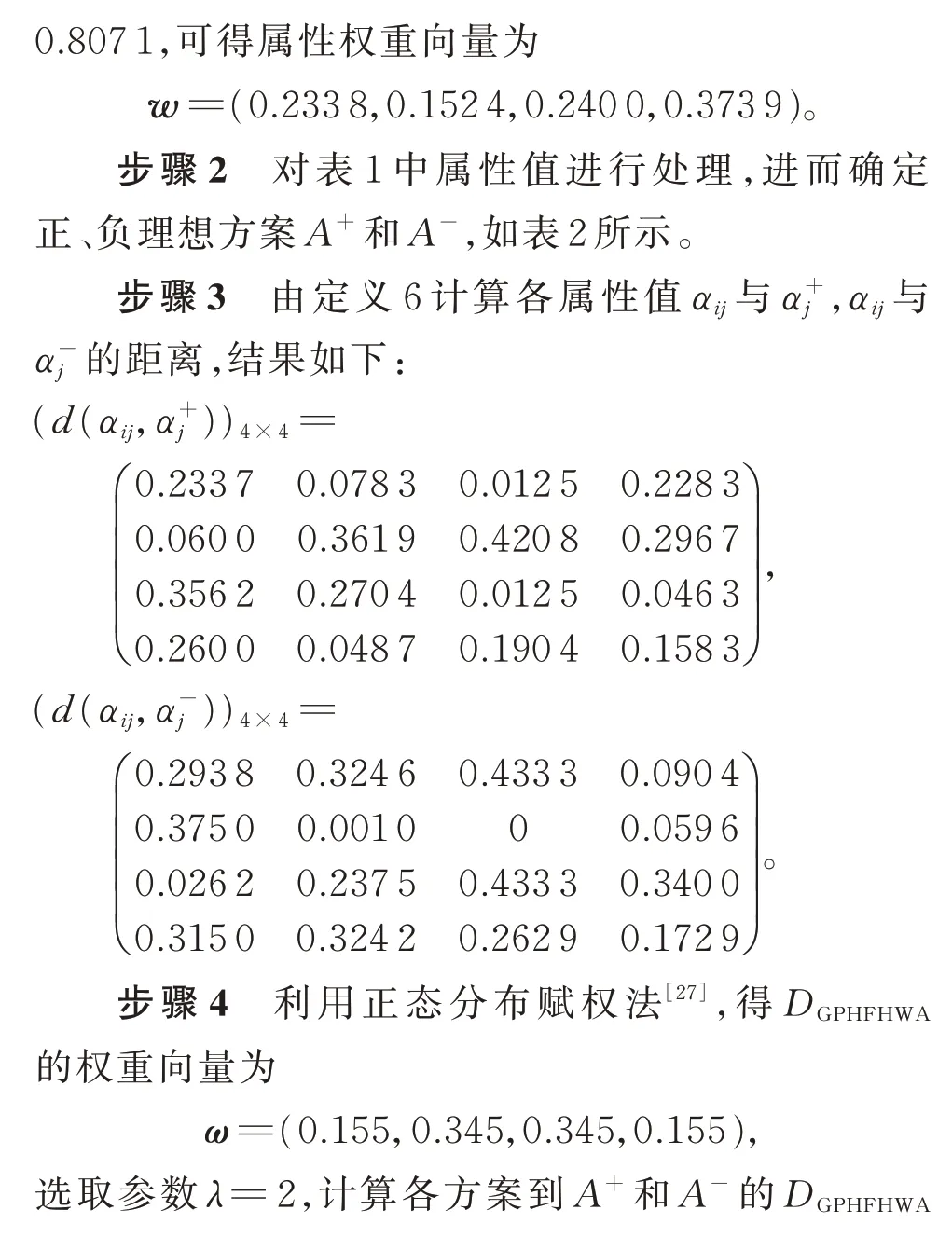
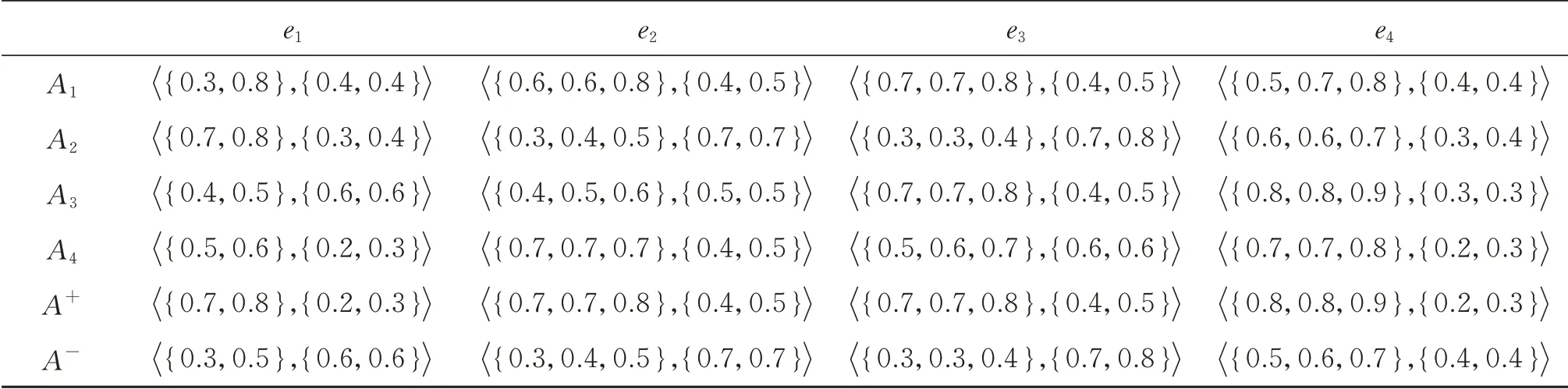
表2 处理后的毕达哥拉斯犹豫模糊决策矩阵Table 2 The processed Pythagorean hesitant fuzzy decision matrix

4.2 算例分析

首先，考虑DGPHFHWA算子中参数λ的取值对决策结果的影响，当λ取不同值时，所得排序结果如表3 所示。可知：（1）当λ→0 和λ=0.2 时，排序结果均为A1≻A3≻A4≻A2，而当λ≥0.5 时，排序结果为A3≻A1≻A4≻A2，λ值确实对排序结果产生了影响；（2）随着λ的增大，A1，A3，A4的贴近度有不同程度减小，而A2的贴近度逐渐增大，当λ≥0.5 时，排序结果呈稳定状态，但方案间的区分度随λ的增大而减小；（3）在所有排序中，A2均为最劣，这与表1 中A2的各项属性值相对较弱这一实际情况一致。可见，基于DGPHFHWA测度的决策方法具有一定的灵活性和较强的稳定性，可满足决策者的目的和需求。

其次，如果在步骤4 中将DGPHFHWA替换为DPHFWA或DPHFOWA，其排序结果如表3 所示。可见，这2 个距离测度所得结果各不相同，且均与DGPHFHWA有差别。这是由于DPHFWA仅考虑属性权重，而DPHFOWA仅考虑位置权重，二者在集成数据时角度不同。基于DGPHFHWA的决策方法可兼顾属性权重和位置权重，集成结果更为全面、合理。

文献［17］所提出的基于毕达哥拉斯犹豫集成算子的方法得到的排序结果为A3≻A4≻A1≻A2，文献［18］基于相似度的方法得到的排序结果为A3≻A1≻A4≻A2，这2 种结果在表3 中均有体现，说明本文所提方法更具一般性。值得注意的是，在λ≥0.5 时文献［18］基于相似度的方法与本文方法的排序结果相同，这是由于相似度和距离测度为模糊集关系的2 个重要度量，均可用于描述模糊集的差异性。

表3 不同距离测度下的排序结果Table 3 Ranking results under different distance measures

5 结束语

在PHFN 的距离基础上，定义了广义PHFS 混合加权距离测度（DGPHFHWA）。该距离测度既考虑元素的重要性，又可通过选定位置权重，避免数据过大或过小对结果造成影响，从而提高PHFS 之间测度结果的科学性。其次，针对属性值为PHFN 的多属性决策问题，利用毕达哥拉斯犹豫模糊指数熵确定属性权重，并提出基于广义PHFS 混合加权距离测度的决策方法，该方法可通过选取参数λ，满足决策者的不同目的和需求。通过算例分析和方法对比，得到本文方法是合理的，其结果更具一般性，可为决策者提供更多的决策机会。值得注意的是，DGPHFHWA不仅适用于TOPSIS 法，还可应用于如投影法、幂集成算子等决策方法，以及群决策问题等，具有一定的应用价值。综上，文中所提的DGPHFHWA和决策方法是对毕达哥拉斯犹豫模糊决策理论的补充。如何定义不受决策者态度影响，且直接反映毕达哥拉斯犹豫模糊原始信息的距离测度，是值得进一步研究和探讨的问题。