倪成才 方昆升 唐小焱

（1. 北华大学林学院，吉林 吉林 132013；2. 广州天权信息科技有限公司，广东 广州 510635；3. 贵州财经大学大数据应用与经济学院，贵州 贵阳 550005）

林分的优势木平均树高(简称优势树高)主要受立地质量和林分年龄的影响[1]。为了对比不同年龄林分的立地质量，需要将林分的优势树高转换为一个特定林龄时的树高，以消除林分林龄对优势树高的影响效应，此特定林龄称为指数年龄，指数年龄时的优势树高称为立地指数，是林业上在衡量立地质量的重要量化指标[2]。

在林学上，将现时林分优势树高转化为立地指数的模型称为立地指数模型[3]。目前，广泛应用的立地指数模型为Clutter 和Bailey 于1974 年提出的差分模型[4]，以及Cieszewski 和Bailey 于2000 年提出的广义差分模型[5]。差分型立地指数模型假设在理论生长模型中，例如理查德方程，仅有一个随林分(立地质量)变化而变化的可变参数，如果指定渐近线参数(asymptote)为可变参数，则可以导出单型模型；而指定渐近线以外的参数为可变参数时，则可导出多型模型[3]。

差分型立地指数模型根据一个林分在现时t1时的优势树高h1来估计在指数年龄t2时的树高h2，模型给出的h2估计值和实测值间必然存在差异，其受多个随机因素的影响，包括t2和t1间的距离、模型参数的估计误差、以及与h1和h2分别相关联的随机误差项等[1-3]。本文以实测数据为基础，对估计误差的行为模式进行经验性分析。

1 材料与方法

1.1 立地指数模型

本文考虑的理论生长方程包括豪斯费尔德（Hossfeld）、考尔夫（Korf）、理查德（Richards）[2]、威布尔（Weibull）、单分子（Mitscherlich）以及逻辑斯蒂（Logistic）模型[3]，均为三参数的生长方程。由于单分子和逻辑斯蒂模型拟合残差均方明显高于其它生长方程，因而在后续分析不予考虑，仅以表1 中4 个模型为基础模型，并推导出了8 个差分型生长模型，单型和多型模型各有4 个，均同时列于表1。

1.2 数据

数据来源于110 个黑云杉Picea mariana 样地优势木的树干解析。样地布设于加拿大哥伦比亚省的黑云杉天然林，面积为0.04 hm2，20 m×20 m。每个样地选取了胸径最大的3 株优势木，每株优势木未经历过任何影响树高生长的损伤、疾病或受压等过程。每株优势木在0.3、0.8 和1.3 m 处，以及胸高以上每隔1 m 处截断，查取年轮数，并纵切获取树高数据。

表1 理论生长模型及导出的差分立地指数模型Table 1 Theoretical growth functions and derived ADA site index models

1.3 估计误差的分析方法

所用数据为树干解析逐年的年龄和树高。对于模型拟合来说数据过多，也与现实中重复观测的优势树高的数据不同，因而通过SAS 的IML 过程，以样地测量时林龄为起点，从树高生长序列中每隔10 年提取一组树高—年龄的数据，共计5次，以模仿实际应用中的重复观测数据。

表1 中的8 个立地指数模型用SAS9.2 的nlin过程拟合，采用了分类变量回归法拟合模型，其技术细节可参考Cieszewski 等[6]。在完成模型拟合后，需要分析每一个模型的立地指数估计误差的行为模式和变化规律。假设有n 个样地的数据，给定第i 个样地在年龄t1时的优势树高为hi,1，估计在指数年龄t2时的树高 hˆi,2(立地指数)，所有样地的估计误差均方(MSE)可定义为

由于差分模型通过一个年龄时(t1)树高(h1)估计另一个年龄时(t2)的树高(h2)，因而又常称之为投影模型。立地指数常用于作为林分特征预估方程的预测变量，例如蓄积和胸断面积等。式(9)中MSE 可用于近似地代表从(t1, h1)投影到(t2, h2)的估计误差的方差，便于评估立地指数估计误差对其它林分特征的预测误差的影响效应(误差分量)。通过不同的t1和t2取值组合，可以分析在不同投影长度t1和t2间的距离和投影方向时不同模型的估计误差的变化规律。投影方向指t1和t2间对比关系，例如t1≤t2时，由于投影方向与时间轴一致，因而可称之为正向投影，否则为反向投影。

2 结果与分析

2.1 模型拟合结果

利用SAS 9.2 的nlin 过程拟合了表1 中8 个差分指数模型，各模型的参数估计值和拟合残差均方列于表2。由于各模型均有3 个参数，因而可以用拟合残差均方对比拟合效果。一般而言，源于同一理论方程的多型模型优于单型模型。模型(2)的拟合残差均方值最小，为0.353 0 m2，但与其它多型模型相比，优势并不明显。

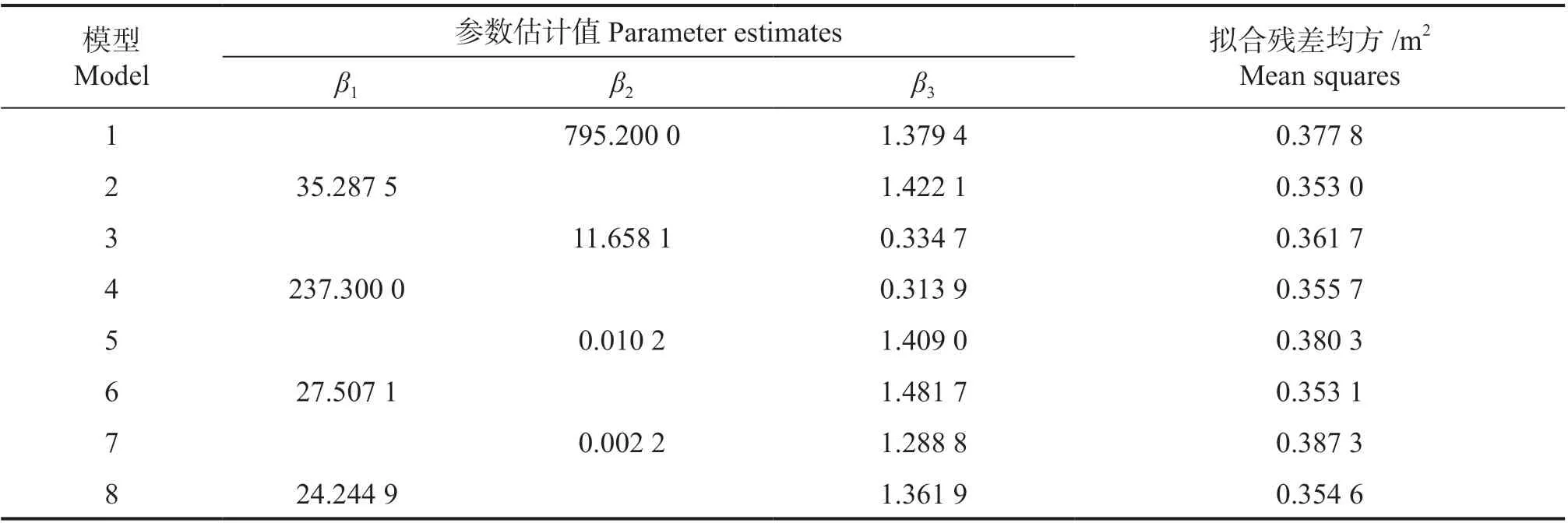
表2 选用的立地指数模型的参数估计值Table 2 Parameter estimates for selected site index models

由于误差均方(MSE)与预测误差的方差密切相关，可用于评估立地指数对其它林分特征预估准确性的影响效应，因而如下的分析将以误差均方(MSE)为主，以平均相对误差(MRE)为辅。

2.2 估计误差的经验性分析

不同投影方向和投影距离时，代表性的MSE行为模式示意于图1 和2。图1 和图2 分别给出了当t1=100 和60 时随t2值变化的误差均方(MSE)的变化模式。当t2=t1时MSE 值为0，所有的差分指数模型包括广义差分模型，均有这一性质，例如表1 的8 个模型均如此。

图1 估计误差均方随指数年龄t2 的变化趋势(t1=100)Fig. 1 The trends of mean squared estimate error with t2 at t1=100

图2 估计误差均方随指数年龄t2 的变化趋势(t1=60)Fig. 2 The trends of mean squared estimate error with t2 at t1=60

估计误差均方(MSE)一般随投影距离增加而增加。当t2＞t1时(正向投影)，一般表现为随投影距离的增加而单调增加；但当t2＜t1时(反向投影)，MSE 首先随投影距离而增加，达到一个峰值后再逐渐下降，如图1 所示。

在投影距离一定时，反向投影(t2＜t1时)的MSE 往往明显低于正向投影(t2＞t1时)。假设林分现时年龄t1=60，如果投影距离为20 年，图2显示反向投影的MSE 约为0.35 m2，但正向投影的MSE 则约为0.90 m2。一般而言，反向投影的MSE 值一般均在可接受的范围之内。从图2 可见，从t1=60 投影到t2=140 时，立地指数的估计误差均方最高可达10 m2。

在投影距离和方向均相同时，多型模型的MSE 往往显著地少于单型模型。在图2 中共计有8 个立地指数模型的估计误差MSE 曲线，单型和多型各有4 个。在80 到140 年的范围内，多型和单型MSE 变化曲线自然地汇聚而成2 个截然不同的曲线族。单型曲线的MSE 相互重叠，位于图2上方，相互间几乎无法分辨，表现出了高度一致的行为模式；而多型曲线则位于下方，表现出一致的、与单形曲线完全不同的MSE 变化规律，且MSE 值系统地显著少于单型曲线，例如当t2=140时，多型模型的MSE 约为6 m2，而单型模型的MSE 却高达10 m2，参考图2。

平均相对误差(MRE)行为模式的代表性结果示于图3 和4。MRE 同MSE 相比，行为模式基本一致，MRE 同样表现出了随投影距离延长而增加的趋势，而且单型曲线也内部趋势一致，与多型曲线截然不同，MRE 往往明显高于多型曲线。MRE 和MSE 相比，也有几点不同。第一点，在反向投影(t2＜t1)时，MRE 表现出一定程度的单调性，随着投影距离的延长MRE 单调增加，并不存在一个类似于MSE 的峰值。第二点，正向投影的MRE 随投影距离增加速度低于反向投影，这一点也与MSE 不同。

图3 平均相对误差随指数年龄t2 的变化趋势(t1 =100)Fig. 3 The trends of mean relative error with t2 at t1 =100

图4 平均相对误差随指数年龄t2 的变化趋势(t1=60)Fig. 4 The trends of mean relative error with t2 at t1=60

3 结论与讨论

从以上分析可见，在估计立地指数时应尽量地避免长距离投影(预测)，以减少估计误差，因而需要确定合理的指数年龄(t2)以降低投影距离。关于指数年龄的讨论可参考陈永富[7]的报道。从控制MRE 角度看，一方面要通过合理的指数年龄降低投影距离，另一方面则需要尽可能地减少反向投影。但从MSE 角度看，特别是当立地指数将作为其它林分特征(例如蓄积)的预测变量时，则在确定指数年龄时应尽量减少正向投影，因为较大MSE 可能极大地降低目标林分特征的预测准确性。无论MRE 或MSE，均要求应根据总体的林龄结构，以及各林龄的面积比例系数等因素来确定指数年龄，而不可以随意指定。这一结论与差分模型的指数年龄无关性(base-invariance)并不矛盾，因为这一属性仅为差分模型的期望方程的一个性质。