孟 彬,韩燕苓

齐鲁工业大学(山东省科学院) 数学与统计学院,济南 250353

曲线的几何特征可以由曲线的弯曲程度刻画,曲线的弯曲程度称为曲线的曲率[1]；三维欧氏空间中,曲线的几何特征不仅可以用弯曲程度刻画还可以用扭曲程度刻画,空间曲线的扭曲程度称为曲线的挠率[1]。曲率在轨道设计、桥梁设计等方面有着重要的应用,陈志刚等[2]介绍了利用曲率类属性预测储层裂缝的应用。挠率在生活中也起着不可或缺的作用,C Blankenburg等[3]给出了3D图像中曲线挠率的估计。除曲线外,曲面几何特征也可由曲面的曲率刻画,曲面曲率在图像处理和地形分析等方面有着重要的作用,文献[4]至文献[6]介绍了曲面曲率的求法及应用。

曲率是探索曲线几何特征最重要的概念之一,本文的主要任务是计算平面、空间曲线的数值曲率,特别是离散点的数值曲率。

1 解析方法

对于平面(空间)上任何一条正则曲线C,都可以用显函数y=f(x)或者隐函数F(x,y)=0来表示,显函数和隐函数都可以表示成向量函数

r(t)=(x(t),y(t))或

r(t)=(x(t),y(t),z(t))。

(1)

定义[1]设曲线C的方程为r(s),其中s是曲线的弧长参数。

(2)

1.1 平面曲线

解析方法:当曲线(1)的参数t是弧长参数s时,曲率的经典计算公式[1]为：

k(s)=|r''(s)|。

(3)

弧积分的被积函数是向量函数导函数的模长,若模长不是常数,被积函数通常含有开方运算,弧积分计算困难。于是,在平面曲线中,(3)式只适用于计算向量函数模长为常数的曲率。

例1:计算r(t)=(3sint,3cost),t∈(0,2π)的曲率。

解:上述曲线的参数不是弧长参数,首先将参数用弧长参数表示：

(4)

将(4)式代入原式

由公式(3)

例1的导函数模长是一个常数,所以参数t可以表示为弧长参数s,但是一般情况下弧积分不能表示为关于t的次数为1的单项式,所以很难用弧长参数表示任意参数,这使得计算曲率的解析解非常困难。

1.2 空间曲线

由于空间曲线存在法向量,本文首先引入空间曲线的两个法向量[1]:

2)次法向量:曲线的切向量和主法向量唯一确定了曲线的次法向量γ(s)=α(s)×β(s)。

当曲线r(s)=(x(s),y(s),z(s))的参数是弧长参数时,可直接由公式(2)计算曲线的曲率。当k(s)≠0时,对两个法向量及其切向量做若干次微分运算以及内积运算(陈维桓,微分几何[1])后,可推导出求解空间曲线曲率的计算公式。

解析方法:对空间曲线的任意参数t,曲线曲率的经典计算公式[1]为

(5)

例2:计算曲线r(t)=(5sint,5cost,3t),t∈(0,2π)的曲率。

解:由公式(5)需要计算曲线的一阶导函数、二阶导函数及其向量积:

r'(t)=(5cost,-5sint,3),

r''(t)=(-5sint,-5cost,0),

r'(t)×r''(t)=(15cost,-15sint,-25),

在实际生活中,如果需要计算曲率的对象是一些离散点而不是函数表达式时,很难用公式(3)和(5)计算曲率的解析解。此外,曲率的计算无论是在桥梁设计还是轨道设计等方面都有很重要的应用,所以计算曲率很有必要。由本节内容得知计算曲率的解析解有很多局限性,于是本文给出一种计算曲线曲率数值解的方法。

2 数值方法

定理1[1]:设α(s)是曲线C的单位切向量,s是弧长参数,用Δθ表示α(s)与α(s+△s)之间的夹角,则

由定理1与图1以及向量夹角与内积的关系,本文给出一种曲线曲率的计算公式。

图1 曲线方向向量与夹角

定理2:设曲线C是一条正则参数曲线,它的方程为r(t),其中t是任意参数,s是弧长,Δs是弧长增量,若极限

(6)

存在,则曲线C在t0点的曲率为k(t0)。

证明:由定义及定理1

(7)

平移α(s)与α(s+△s)至同一起点(图1),α(s)与α(s+△s)夹角的余弦值可以由α(s)与α(s+△s)的内积表示

(8)

(9)

夹角的大小与参数无关,所以

(10)

将(10)式代入(7)式

公式(6)是由内积与夹角余弦的关系得到的,虽然此式也可以用来计算曲率解析解,但是反三角函数不易计算具体值,所以此式最主要用于计算曲率数值解。

特别,若正则曲线是一段圆弧,则曲率可用圆弧所在圆的半径表示。

推论:设曲线C是一段圆弧,它的方程为r(t),其中t是角度参数,R是圆弧所在圆的半径,此时曲率可表示为

(11)

证明:由图2,当曲线是圆弧时Δt=Δθ,所以

图2 参数增量与方向向量夹角的关系

化简后取极限

(12)

设圆弧的向量函数为r(t)=(Rsint,Rcost),t∈(θ1,θ2),则|r'(t)|=R,所以(12)可写为

当曲线C是一段圆弧时,计算曲率只需要求曲线C的导函数,这大大降低了计算曲率的难度,并且(11)式既便于计算曲率解析解也便于计算曲率数值解。

定理3 设曲线C是一条正则参数曲线,方程为r(t),其中t是任意参数,Δt是参数t的增量,Δs是弧长增量(t是弧长参数时Δt=Δs),令k-(t0)、k+(t0)分别为t0的左、右曲率,若左曲率

(13)

与右曲率

(14)

均存在,则

k(t0)=k-(t0)=k+(t0)。

在三维欧氏空间中,(10)式仍然表示曲线切向量的夹角,但圆弧曲线中Δt不再等于切向量的夹角Δθ(实际上等于两切向量夹角的方向余弦),所以(11)式只适用于求平面圆弧曲线的曲率,而(6)式中切向量的夹角在空间中的计算方法不变,所以(6)式也适用于计算空间曲线的曲率。

3 MATLAB程序实现

3.1 验证公式

本小节通过计算连续函数离散化后点的数值曲率验证曲率计算公式(6)和(11)在实际问题中的适用性。

例3:编程计算y=sinx的数值曲率。

由上表可以看出误差的阶数都是10-3,而步长取定为10-2,误差小于步长。

表1中误差是直接将MATLAB计算出的结果与解析解(精确到小数点后15位)比较后的误差,但通过MATLAB计算的数值结果与精确解(精确到小数点后15位)的关系可以看出,tk处的数值解与tk+1处的精确解“几乎相等”。

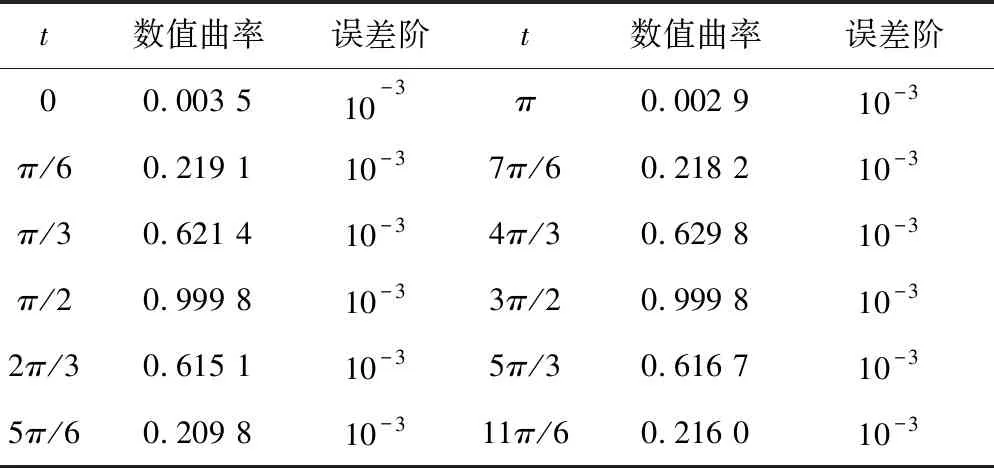
表1 y=sinx数值曲率

选用向后差商公式[7]计算数值导数并按照左曲率公式(13)编程得到tk的数值曲率的值恰为表2中数值曲率tk+1的值,数值曲率与误差如下表所示。

表2 数值解与精确解

对比表2与表3,数值导数公式的选取不同会导致数值曲率的计算结果不同。

表3 数值曲率与误差

例4:编程计算y=x3,x∈(0,3)的数值曲率。

表4表明,用向前差商公式求数值导数和右曲率公式(14)编程求数值曲率的结果不存在表2中数值解与解析解“错位”的问题。同时再用向后差商公式求数值导数和左曲率(13)编程求数值曲率的结果与表4结果相同。

表4 数值解与精确解

在MATLAB中可以求符号函数的极限(文献[8]至文献[10]给出了用MATLAB计算正则参数曲线弧长、导数、极限以及曲率解析解的相关介绍及MATLAB程序)但无法求离散数据的极限,在取极限运算时往往以小步长近似极限,所以表2与表3的结果可看作小步长下的左曲率(13)与右曲率(14)。在极限运算下左曲率与右曲率是相等的,但在离散数据的MATLAB编程中数值导数或左、右曲率的选择不同数值曲率的计算结果也不同。

例3和例4表明,数值导数选向前差商公式时配合右曲率编程计算数值曲率的结果与数值导数选向后差商公式时配合左曲率编程计算数值曲率的结果相同,并且计算结果的精度优于另外两种组合。表3与表4的结果表明,步长取Δt=0.01,除个别端点外误差均小于Δt2,误差可由步长控制。

例5:编程计算例1的数值曲率。

解:首先引入求数值导数的三点公式[11]:

由公式(11)可知,圆的曲率是半径的倒数,当半径是3时,曲率解析解为1/3,取步长0.01,用三点公式求数值导数,对公式(11)编程计算,得到结果如下表。

表5 例1的数值曲率

由上表可以看出,数值曲率的误差阶是10-6,而步长是10-2,误差可由步长控制。改变步长对比计算结果发现,当误差达到10-9后很难再减小,原因在于MATLAB软件本身含有存储误差以及计算时产生的截断误差。

通过例3、例4和例5验证了公式(6)和公式(11)适用于计算离散点处的数值曲率。计算数值曲率时可以直接用离散公式(5),但由于公式(5)需要计算向量函数的二阶导数,这会增大数值曲率计算的误差,而(6)式只需要计算向量函数的一阶导数,理论误差要小于(5)式。

例6:分别用公式(5)和公式(6)编程计算曲线r(t)=(5sint,5cost,3t),t∈(0,2π)的数值曲率。

解:由例2可知正螺旋线的曲率是5/34,取步长0.01,用向前差商公式求数值导数,编程得到结果见表6:

表6 数值曲率

由上表可以看出,除最后一个点外,公式(5)的误差都是10-6阶,而公式(6)的误差都是10-7阶,所以公式(6)的计算结果要好于公式(5)。除此之外,通过改变本例的步长发现,随着步长的减小误差很难再有大幅度的减小,原因是存在截断误差。上表中,公式(5)与公式(6)最后一个数值曲率均为0,这是由于求数值导数时使用的是向前差商法,差商法只能求(n-1)个点的数值导数(n为离散点的个数),为使计算时维度相同,可令tn的数值导数为向后差商,这使得最后两个数值导数的值是相同的,所以最后一个点的数值曲率为0。用三点公式计算最后一点的数值导数可避免最后一个数值曲率为0的情况。

由以上四个例子可知,公式(6)与公式(11)适用于计算离散点处的数值曲率,并且本文例题指出数值曲率的误差精度不会低于步长的精度。

3.2 实际应用

曲率半径与向心力的计算有直接的关系,所以曲率半径在铁路、高速等轨道设计中起着至关重要的作用。

例7:给定一组离散数据,计算各点处的数值曲率。

表7 离散数据

解:根据公式(6)编程计算可得各点处的数值曲率如表8。

表8 离散点的数值曲率

离散点图像与数值曲率图像:

由图3可以看出:沿着x轴正方向,曲线相邻点的切线夹角随着x趋于正无穷逐渐趋于0,与图4数值曲率走势相吻合。

图3 离散点图像

图4 数值曲率图像

4 总 结

平面曲线和空间曲线的数值曲率都可以用公式(6)求解,但是在计算数值导数时选用的数值算法不同会导致计算结果的精度不同。例题3至例题5表明,不管用向前(有的是向后)差商公式还是三点公式求数值导数,得到结果的精度都不会低于步长的精度,所以数值曲率的精度可由步长控制。对于公式(6)而言,它需要计算反三角函数,计算曲率的解析解没有普适性；对于公式(11)而言,它既可以用来计算数值曲率也可以计算解析曲率。通过编程计算发现:随着步长的无限减小,误差精度很难再有提升,原因在于MATLAB的存储误差以及在计算时产生的截断误差。