马艳丽，聂东明，于 萍

(安徽新华学院 通识教育部，合肥 230088)

0 引 言

传染病是危害人类身体健康的大敌，传染病的防治一直受到高度重视。世界各国政府和研究机构采取了一系列的预防和控制措施，已取得辉煌的成果。但是，随着经济发展的全球化，生态环境的变化及病原体抗药性的增强，一些已被灭绝或治愈的传染病和一些新出现的传染病呈现出全球化传播和发展的趋势。因此，不管是国内还是国外对传染病进行有效的预防和控制都是刻不容缓的。

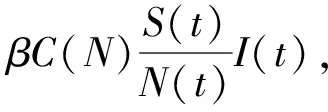
此外，为了有效地预防和控制传染病的发生和发展，通常采取相应的预防和控制策略，并且同样的防控策略可以用不同的方式来体现，如有连续接种与脉冲接种、连续剔除与脉冲剔除等[8]。目前已有大量的文献[9-13]研究了连续方式的预防和控制策略对传染病流行的影响，但关于不同预防和控制措施的混合且对各种防控措施进行比较的文献还不多见。针对上述情况，本文将连续方式的接种、剔除和隔离干扰引入模型，建立了一类具有非单调传染率的SIQR传染病模型，从理论研究和计算机模拟方面分析了无病平衡点和地方病平衡点的存在性以及全局稳定性。

1 模型的假设及建立

根据上述假设和说明，可以得到如下SIQR仓室结构，如图1所示。

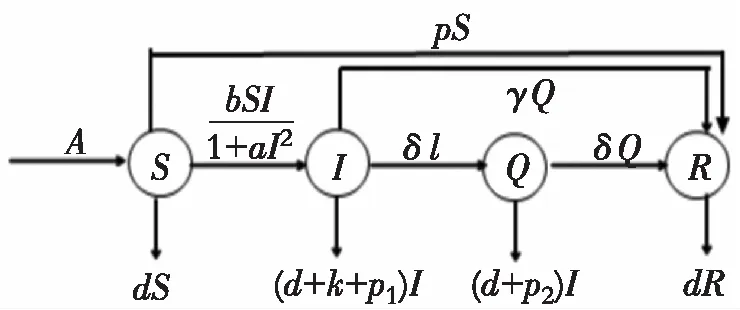
图1 SIQR传染病模型框图

得到相应的SIQR微分方程模型:

(1)

2 平衡点的存在性分析

对于式(1),令d+p1+γ+δ+k=m，ε+d+p2=n，则可以得到如下系统:

(2)

(3)

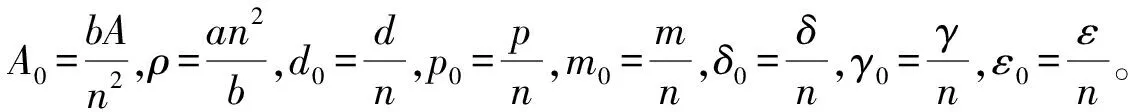
总人群令为N(t)，N(t)=S(t)+I(t)+Q(t)+R(t)。由式(3)可得到总人群方程:

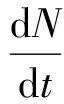
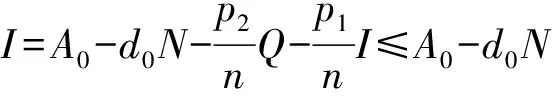
从而得到:

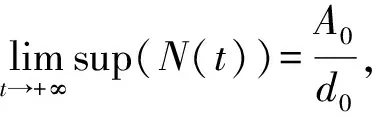
且D是式(3)的一个最大正向不变集。

令式(3)中各个方程的右端项等于零:

(4)

通过计算得到式(3)的无病平衡点：

当S=m0(1+ρI2)时，得到:

m0(d0+p0)ρI2+m0I+m0(d0+p0)-A0=0

(5)

定义疾病流行与否的阈值-基本再生数：

当R0>1时，由式(4)和(5)得到式(3)的唯一地方病平衡点E*(S*,I*,Q*,R*)，其中：

综上讨论可以得到如下定理:

定理1 式(3)总存在无病平衡点E0；当R0>1时，式(3)还存在唯一的地方病平衡点E*。

3 无病平衡点的稳定性分析

定理2 当R0<1时，式(3)的无病平衡点E0是局部渐近稳定的；当R0>1时，无病平衡点E0是不稳定的。

证明当基本再生数R0<1时，在无病平衡点E0处，式(3)的雅可比矩阵是

矩阵J(E0)的特征方程为

(λ+d0+p0)(λ+m0(1-R0))(λ+1)(λ+d0)=0

可得4个特征值分别为

λ1=-(d0+p0)，λ2=m0(R0-1)

λ3=-1，λ4=-d0

当R0<1时，λ1<0，λ2<0，λ3<0，λ4<0，即矩阵J(E0)的一切特征值的实部都是负数，所以，式(3)的无病平衡点E0具有局部渐近稳定性；当R0>1时，特征值λ2>0，即矩阵J(E0)至少存在一个特征值，它的实部是正数。因此，无病平衡点E0在闭集D内是不稳定的。

定理3 当R0<1时，式(3)的无病平衡点E0是全局渐近稳定的。

证明根据式(3)的第一个表达式可以得到

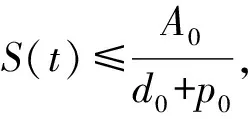
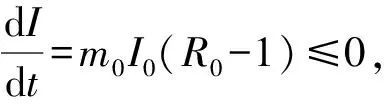
(6)

解式(6)中的第一个和第二个方程可以得到:

从而得到:

(7)

将式(7)代入式(6)中的第3个表达式得到如下结果:

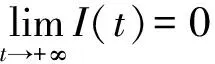
4 地方病平衡点的稳定性分析

定理4 当R0>1时，式(3)的地方病平衡点E*局部渐近稳定。

证明在地方病平衡点E*处，系统式(3)的雅可比矩阵是

则矩阵J(E*)的4个特征值分别为λ1，λ2，λ3=-1<0，λ4=-d0<0，其中特征值λ1和λ2也是二阶矩阵

的特征根，即是方程λ2+a1λ+a2=0的两个根，其中，

由Hurwitz判据，在方程λ2+a1λ+a2=0时，有

H2=a1a2=

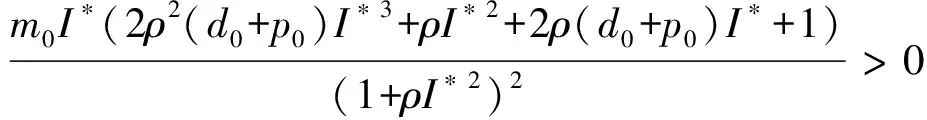
即特征值λ1<0，λ2<0。又由于特征值λ3=-1<0，λ4=-d0<0，从而得到矩阵J(E*)的一切特征值的实部都是负的。所以，当R0>1时，式(3)的地方病平衡点E*局部渐近稳定。

定理5 当R0>1时，式(3)的地方病平衡点E*全局渐近稳定。

证明因为式(3)的前两个式子不含有Q和R，故研究式(3)的子系统:

(8)

对于式(8)，构造Liapunov函数:

则V(t)是正定函数，因为V(t)沿着式(8)的导数有:

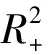
考虑式(3)的第三个方程，可以得到其极限方程为

借助洛必达法则得到:

同理，可以计算出:

所以，在区域D上，式(3)的地方病平衡点E*具有全局吸引性，结合定理4，故则当R0>1时，式(3)的地方病平衡点E*是全局渐近稳定的。

5 计算机模拟

在式(3)中，选取参数A0=0.2，ρ=3，d0=0.4，p0=0.2，m0=0.5，γ0=0.1，δ0=0.2，ε0=0.4。取 6组不同的初值分别为S(0)=0.15，I(0)=0.03，Q(0)=0.2，R(0)=0.3；S(0)=0.075，I(0)=0.025，Q(0)=0.1，R(0)=0.05；S(0)=0.2，I(0)=0.05，Q(0)=0.03，R(0)=0.1；S(0)=0.25，I(0)=0.05，Q(0)=0.16，R(0)=0.2；S(0)=0.4，I(0)=0.1，Q(0)=0.08，R(0)=0.12；S(0)=0.1，I(0)=0.2，Q(0)=0.05，R(0)=0.15。通过计算可得R0=0.666 7<1，无病平衡点E0=(0.333,0,0,0.167)，利用Matlab软件对式(3)进行数值模拟可以得到图2。

图2 R0=0.666 7时，6组不同初值时的无病平衡点的全局稳定性示图

选取参数A0=4，ρ=0.02，d0=0.5，p0=0.2，m0=0.8，γ0=0.1，δ0=0.1，ε0=0.25。取6组不同的初值分别为S(0)=0.6，I(0)=3.4，Q(0)=2.2，R(0)=4.5；S(0)=1.5，I(0)=3，Q(0)=2.4，R(0)=4；S(0)=3.5，I(0)=0.5，Q(0)=1.8，R(0)=2；S(0)=2.5，I(0)=1.6，Q(0)=0.9，R(0)=3.4；S(0)=3，I(0)=1.2，Q(0)=4，R(0)=2.6；S(0)=2，I(0)=2.6，Q(0)=0.5，R(0)=1.5。通过计算可得R0=7.142 9>1，地方病平衡点E*=(1.065,4.068,0.408,1.446)，利用Matlab软件对式(3)进行数值模拟可以得到图3。

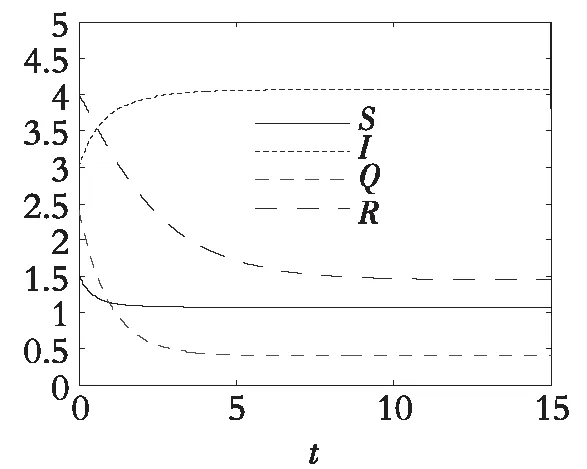
图3 R0=7.142 9时，6组不同初值时地方病平衡点的全局稳定性示图

由图2和图3可以看出，对于选定的初值，当R0<1时，对于式(3)的解(S,I,Q,R)都趋向于无病平衡点E0，从而证实定理3是正确的；当R0>1时，式(3)的解(S,I,Q,R)都稳定于地方病平衡点E*，从而说明定理5的准确性。

6 接种、剔除和隔离策略的比较和分析

(9)

(10)

(11)

由式(9)(10)和(11)可以得到，Δp<0，Δδ<0，Δk<0，因此，在对传染病进行预防接种、隔离和剔除策略后，都可以减少基本再生数R0，从而有利于控制传染病的发生和传播。

由式(10)(11)可以得到，Δδ=Δk，从而说明代表隔离强度的参数δ，与代表剔除强度的参数k，对于基本再生数的影响是相同的。在其他情况不变的条件下，从基本再生数的角度看来，隔离和剔除策略对于疾病流行性态的影响是相同的。但从实际角度看来，隔离的种群需要花费很大的治疗成本，而剔除则花费的成本较小。因此，对于没有限制的如动物种群，可以用剔除的方法来消除疾病，但对某些种群，剔除策略是不可行的，而隔离无疑成了替代的方式。

由式(9)(10)可知，Δp≠Δδ，即接种策略对于基本再生数的影响不同于隔离策略。将Δp与Δδ做比值，得到:

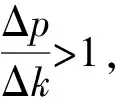
但是，从实际的角度出发，由于易感者S(t)的数量通常大于染病者I(t)的数量或隔离者Q(t)的数量，增加单位预防接种比例的成本远远高于改善单位隔离成本或剔除成本。因此，在实施预防和控制传染病的实际策略时应考虑混合策略的情况，使得成本和效益最佳。

7 结 论

将连续方式的接种、剔除和隔离干扰引入模型，构建了一类具有非单调传染率的SIQR传染病模型。利用定义法给出了模型的基本再生数R0，通过计算得到了无病平衡点和地方病平衡点的存在性。从理论研究和计算机模拟方面证明了无病平衡点和地方病平衡点的全局稳定性，并借助基本再生数R0的偏导数，对连续方式的接种、剔除和隔离策略进行了比较和分析。本文考虑的接种、剔除和隔离策略是连续方式的，且隔离策略仅仅对染病者实施，对于其他方式，如考虑脉冲方式，或对易感者隔离等问题是今后主要努力研究的方面。

参考文献(References):

[1] 徐文雄，张仲华.年龄结构SIR流行病传播数学模型渐近分析[J].西安交通大学学报，2003，37(10):1086—1089

XU W X，ZHANG Z H.Asymptotic Snalysis of Age Structure SIR Epidemic Spread Mathematical Model[J].Journal of Xi’an Jiaotong University，2003,37(10):1086—1089(in Chinese)

[2] 周美涛.一类具有双线性发生率和常数治疗函数的SIRS传染病模型的动力学行为[J].辽宁工业大学学报(自然科学版)，2015，35(5):344—350

ZHOU M T.Dynamic Behavior of a SIRS Epidemic Model with Bilinear Incidence and Constant Treatment Function[J].Journal of Liaoning University of Technology(Natural Science Edition),2015,35(5):344—350(in Chinese)

[3] 马艳丽，张仲华，聂东明.具有连续接种与剔除的SIQR流行病模型全局稳定性[J].应用数学，2016，29(4):782—787

MA Y L,ZHANG Z H,NIE D M.Global Stability of SIQR Epidemic Model with Vaccination Elimination Strategy[J].Applied Mathematics，2016,29(4):782—787(in Chinese)

[4] 徐金瑞，王美娟，张拥军.一类具有标准发生率的SIS型传染病模型的全局稳定性[J].生物数学学报，2010，25(2):249—256

XU J R.WANG M J,ZHANG Y J.Global Stability of a SIS Epidemic Model with Standard Incidence[J].Journal of Biomathematics，2010,25(2):249—256(in Chinese)

[5] 马艳丽，张仲华.潜伏类和移出类具有传染性的SEIR模型的渐近分析[J].中国科学技术大学学报，2016，46(2):953—103

MA Y L,ZHANG Z H.Asymptotical Analysis of a SEIR Model with Infectious Forcein Latent Period and Immune Period[J].Journal of University of Science and Technology of China，2016,46(2):953—103(in Chinese)

[6] LI G H，JIN Z.Global Stability of a SEI Epidemic Model[J].Chaos，Solitions and Fractals，2004，21(1)，925—931

[7] XIAO D M，RUAN S G.Global Analysis of an Epidemic Model with Nonmonotone Incidence Rate[J].Mathematical Biosciences，2007，208(2):419—429

[8] 章培军，李维德，朱凌峰.SIRS传染病模型的连续接种和脉冲接种的比较[J].兰州大学学报(自然科学版)，2011，47(1):82—86

ZHANG P J,LI W D,ZHU L F.Comparison of Continuous Vaccination and Pulse Vaccination in SIRS Infectious Disease Model[J].Journal of Lanzhou University(Natural Science Edition),2011,47(1):82—86(in Chinese)

[9] MA Y L，LIU J B，LI H X.Global Dynamics of a SIQR Model with Vaccination and Elimination Hybrid Strategies[J].Mathematics，2018，6(12):328—339

[10] 周艳丽，王贺桥.具有隔离和接种策略的传染病模型稳定性分析[J].上海理工大学学报，2010，32(3):249—252

ZHOU Y L，WANG H Q.Stability Analysis of an Infectious Disease Model with Isolation and Vaccination Strategies[J].Journal of University of Shanghai for Science and Technology,2010,32(3):249—252(in Chinese)

[11] TAN X X,LI S J，DAI Q W，et al.An Epidemic Model with Isolated Intervention Based on Cellular Automata[J].Advanced Materials Research,2014,926(1):1065—1068

[12] ECKALBAR J C,ECKALBAR W L.Dynamics of a SIR Model with Vaccination Dependent on Past Prevalence with High-order Distributed Delay[J].Biosystems，2015,129(1):50—65

[13] LI J Q,YANG Y L.SIR-SVS Epidemic Models with Continuous and Impulsive Vaccination Stratgies[J].Journal of Theoretical Biology,2011,280(1):108—116