于学明 李世臣

(1．河南省商水县希望中学 466100；2．河南省周口市川汇区教研室 466001)

文[1]介绍了Philon线的定义及其性质，揭示了在定角内过定点的直线，被角所截最小线段的几何特征．由于过定点的直线可以看作是以定点为顶点的平角，于是我们把平角换成某个定角θ(0°<θ<180°)进行了探究，发现存在类似的Philon线，同样具有优美的几何性质，最后以几何视角诠释了圆锥曲线夹在两条固定切线间切线段长的极值问题．

广义Philon线定义如图1，已知∠MON是定角，点P是角内的一个定点，点A，B分别在射线OM，ON上，∠APB的大小为定值，当线段AB的长度取得极值时，我们称此时的线段是在定角内，以定点为顶点，张角为定值的广义Philon线．

图1

下面探讨广义Philon线的几何特征．

定理如图2，在定角∠MON内，线段AB是以定点P为顶点，张角为定值的广义Philon线．连接OP，若∠AOP=α，∠POB=β，∠BPA=θ，∠PAO=x，∠OBP=y，则

图2

证明设PO=ρ，在△OAP和△OPB中，

由正弦定理得

在△APB中，由余弦定理得

AB2=PA2+PB2-2PA·PB·cosθ

因为α+β+x+θ+y=360°，

所以y=360°-(α+β+θ+x)．

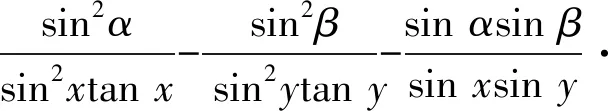
移项整理得

提取公因式后即得(※)式．证毕.

性质1如图3，在定角∠MON内，线段AB是以定点P为顶点，张角为定值的广义Philon线．作AD⊥PB于点D，BE⊥PA于点E，直线OA，OB过点A，B的垂线分别交直线BE，AD于点F，G，连接PF，PG，则S△PAF=S△PBG．

图3

证明如图2，在△OAP和△OPB中，由正弦定理知

代入(※)式得

因为AD⊥PB，BE⊥PA，

则AE=PA-PB·cosθ，

BD=PB-PA·cosθ．

因为AF⊥OA，BG⊥OB，

则∠PAF=x-90°，∠GBP=y-90°,

于是PA·EF=PB·DG,

性质2如图4，在定角∠MON内，线段AB是以定点P为顶点，张角为定值的广义Philon线．直线OA，OB过点A，B的垂线交于点H，则△PAB的外心S在直线PH上．

图4

证明设直线AH，BH，PH分别交PB，PA，AB于点J，I，K，作AD⊥PB于点D，交直线BI于点G，作BE⊥PA于点E，交直线AJ于点F，设直线PH交AB于点K．

对于直线BI截△PAD，直线AJ截△PBE，由梅涅劳斯(Menelaus)定理得

由于AP·FE=PB·DG，

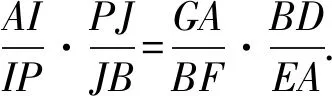
对共点于H的三条直线，

由塞瓦(Ceva)定理得

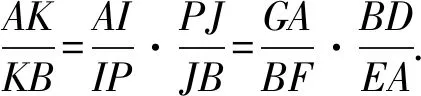
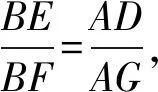
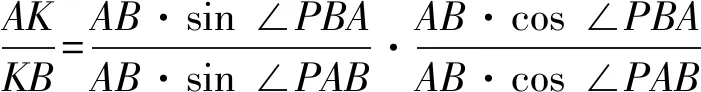
设点K到AP，BP的距离为dK-AP，dK-BP，则

设△PAB的外接圆半径为R，S到PA，PB的距离为dS-AP，dS-BP，则

所以△PAB的外心S在直线PH上．

性质3如图5，在定角∠MON内，线段AB是以定点P为顶点，张角为定值的广义Philon线．HA⊥OM，HB⊥ON，HC⊥PA于点C，HD⊥PB于点D，则CD∥AB．

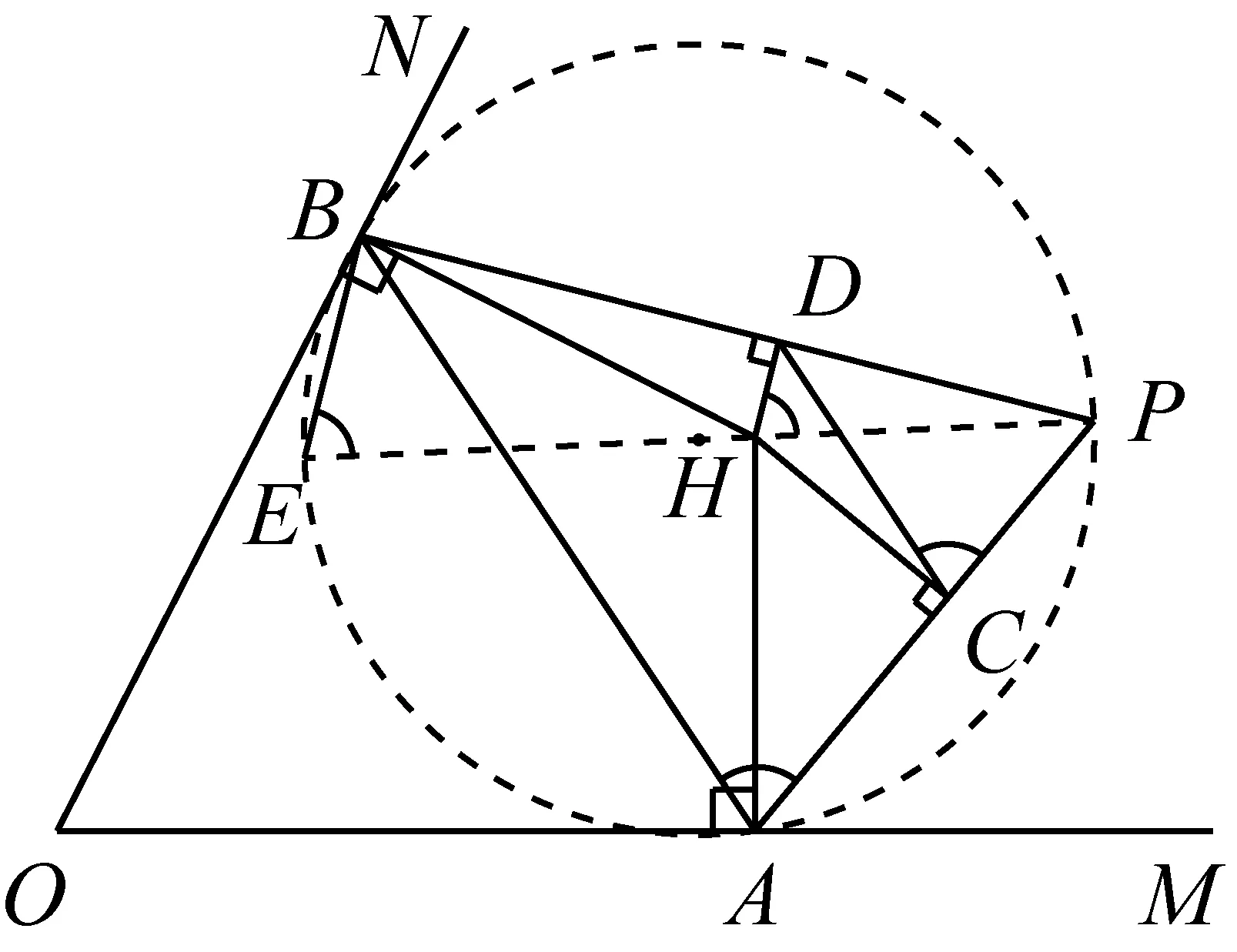
图5

证明设直线PH与△PAB的外接圆另交于点E．

由性质2知，线段PE是△PAB的外接圆直径．

连接BE，则∠BEP=∠BAP，BE⊥BP．

因为HD⊥BP，则BE∥HD，

所以∠BEP=∠DHP．

因为HC⊥PA，HD⊥PB，

所以H，C，P，D四点共圆．

所以∠DHP=∠DCP．

于是∠BAP=∠DCP，所以CD∥AB．

为了以下证明方便引入两个引理．

引理1如图6，线段AB，CD交于点O，△OAC，△OBD的外接圆交于点P，PE⊥AC于点E，PF⊥BD于点F，PG⊥AB于点G，PH⊥CD于点H，连接PA，PB，PC，PD，EF，GH，求证：(1)E，F，G，H四点共线；(2) △PAB∽△PEF∽△PCD；(3) △PAC∽△PGH∽△PBD．

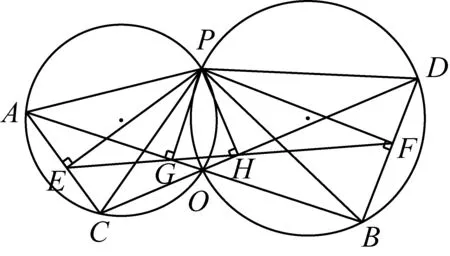
图6

证明(1)因为PE⊥AC，PF⊥BD，PG⊥AB，PH⊥CD，由西姆松定理知，点E，G，H共线，点G，H，F共线．所以E，G，H，F四点共线．

(2)由P，A，E，G；P，E，C，H四点共圆，

所以∠PAG=∠PEG=∠PCH．

同理∠PBO=∠PFH=∠PDH．

所以△PAB∽△PEF∽△PCD．

(3)由P，A，E，G；P，G，B，F四点共圆，

所以∠PAC=∠PGH=∠PBD．

同理∠PCA=∠PHG=∠PDB．

所以△PAC∽△PGH∽△PBD．

引理2如图7，点P是△ABC外接圆上一点，连接PA，点P关于△ABC的西姆松线是l，AG⊥l，则∠PAB=∠CAG．

图7

证明设l与AB，AC分别交于点D，E，连接PD，PE．

因为l是点P关于△ABC的西姆松线，所以PD⊥AB，PE⊥AC．所以A，D，P，E四点共圆，∠PAB=∠PED．

因为PE⊥AC，AG⊥l，

所以∠PED=∠CAG．

所以∠PAB=∠CAG．

性质4如图8，在定角∠MON内，线段AB是以定点P为顶点，张角为定值的广义Philon线．直线OA，OB过点A，B的垂线交点为H，过A，H，P三点的圆与直线PB交于点C，直线AC交过B，H，C三点的圆于点Q，PD⊥AB于点D，QE⊥AB于点E，则AD=BE．

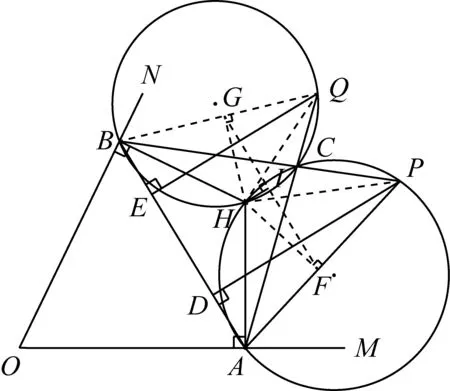
图8

证明连接BQ，HQ，HP，

由引理1(3)知△HAP∽△HQB．

作HF⊥AP于点F，HG⊥BQ于点G．

连接GF，由引理1(1)知，直线GF是点H关于△APC和△BCQ的西姆松线．

由性质3知，GF∥AB．

因为PD⊥AB，QE⊥AB，

所以PD⊥GF，QE⊥GF．

由引理2知∠APD=∠HPC，∠BQE=∠HQC．

作HI⊥GF于点I，由引理1(2)知

∠HFI=∠HPC，∠HGI=∠HQC．

所以∠APD=∠HFI，∠BQE=∠HGI．

所以Rt△APD∽Rt△HFI，

Rt△BQE∽Rt△HGI．

所以AD=BE．

性质5如图9，在定角∠MON内，线段AB是以定点P为顶点，张角为定值的广义Philon线．直线OA，OB过点A，B的垂线交点为H，过A，H，P三点的圆与直线PB交于点C，直线AC交过B，H，C三点的圆于点Q，直线PH交△PAB的外接圆于点J，则JQ⊥AB．

图9

证明作PD⊥AB于点D，QE1⊥AB于点E1，由性质4知，AD=BE1．

作JE2⊥AB于点E2，

由性质2知，PJ是△PAB的外接圆直径．

所以AD=BE2．

于是BE1=BE2，点E1，E2重合．

所以JQ⊥AB．

性质6如图10，在定角∠MON内，线段AB是以定点P为顶点，张角为定值的广义Philon线．直线OA，OB过点A，B的垂线交点为H，HT⊥AB于点T，过A，H，P三点的圆与直线PB交于点C，直线AC交过B，H，C三点的圆于点Q，则∠PTH=∠QTH．

图10

证明作直线PH交△PAB的外接圆于点J，由性质5得JQ⊥AB于点E．

连接JB，则JB⊥BP．作HK⊥BP于点K，

作PD⊥AB于点D，由性质4，AD=BE．

性质4已证∠APD=∠HPK，

∠BQE=∠HQC=∠HBK．

所以,Rt△APD∽Rt△HPK，

Rt△BQE∽Rt△HBK．

因为HT⊥AB于点T，所以PD∥HT∥JE．

所以Rt△PDT∽Rt△QET．

于是∠PTD=∠QTE．

所以∠PTH=∠QTH．证毕.

以上探究了广义Philon线的性质1～6，下面探究其与圆锥曲线的关系．

由文[2]知道：“在椭圆中，一条切线介于两条定切线间的部分，在一个焦点的视角为常量．”逆向思考：一条动直线被两条固定直线所截，所得线段对一个定点的视角为常量，这些动直线的包络是否是一条以定点为焦点的圆锥曲线呢？这一猜想很容易在动态数学软件Geogebra上进行验证，下面仅给出椭圆情形的证明过程．

命题如图11，已知两条定直线的交角∠MON=ω，动直线l交定直线于点Y，Z，线段YZ与定点P的视角∠YPZ=θ为定角．若ω+θ<180°，则l的包络曲线是椭圆．

图11

证明作PD⊥l于点D，PU⊥OM于点U，PV⊥ON于点V，因为ω+θ<180°，则点P在△OYZ的外接圆外部．

由西姆松(Simson)定理知，U，D，V三点不共线．连接DU，DV，由于P，U，Y，D；P，V，Z，D四点共圆，易知∠DPY=∠DUY，∠DPZ=∠DVZ．

在凹四边形OUDV中，∠UDV=∠UOV+∠DUO+∠DVO=∠UOV+∠DPY+∠DPZ=∠MON+∠YPZ=ω+θ．

由条件知U，V是定点，点D是动点，∠UDV是定值，所以D，U，V三点确定一个定圆．设圆心为W，半径WD为a．延长PW至Q，使WQ=PW；延长PD至X，使DX=PD．连接QX，交直线l于点T，则XQ=2WD=2a．连接TP，易知TP=TX，所以TP+TQ=QX=2a(定值)．

由椭圆及其切线的定义知，点T的轨迹是一个椭圆，直线l切椭圆于点T．所以l的包络曲线是椭圆．证毕.

根据广义Philon线的定义和性质判断，在椭圆中，介于两条定切线之间，且取得极值的切线段就是广义Philon线．焦点在这条切线上的射影到切线段端点的距离相等．这样，用广义Philon线直观地解释了圆锥曲线夹在两条固定切线之间切线段长的极值问题．对于抛物线(ω+θ=180°)和双曲线(ω+θ>180°)两种情形可作类似的解释．

本文探讨了广义Philon线的几何特征，关于怎样用已知量来表达极值，以及取得的极值是极大值还是极小值问题有待进一步研究．