■安徽省利辛高级中学 胡 彬

1.（2020 年龙岩模拟）如图1，在四棱锥P-ABCD 中，PA ⊥平面ABCD，在四边形ABCD 中，∠ABC=90°，AB=4，BC=3，CD =，AD=2，PA=4。

（1）证 明：CD ⊥平面PAD；

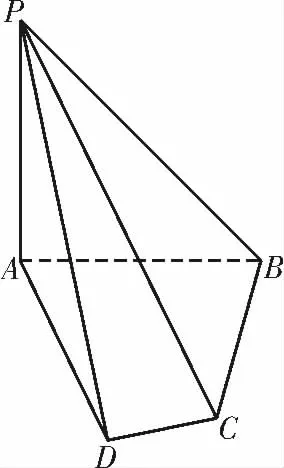
图1

（2）求二面角B-PC-D 的余弦值。

2.（2020 年江西模拟）如图2，在三棱锥P-ABC 中，平面PAC⊥平面ABC，∠BAC=90°，∠ACP=30°，且AC=12，AB=AP=6。

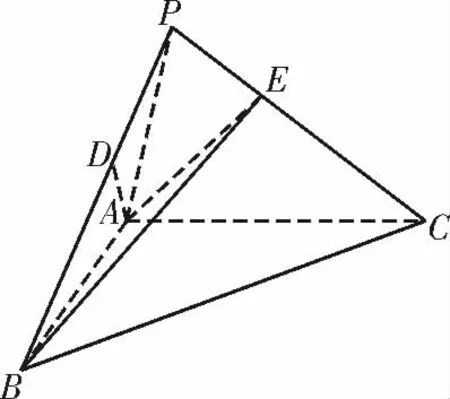
图2

（1）若D 为BP 上的一个动点，求证：PC⊥AD；

（2）若CE=2EP，求二面角A-EB-C 的平面角的余弦值。

3.（2020 年郑州模拟）如图3，四边形ABCD 是矩形，沿对角线AC 将△ACD 折起，使得点D 在平面ABC 内的射影恰好落在边AB 上。

（1）求证：平面ABD⊥平面BCD；

4.（2020年龙岩模拟）如图4，在四棱锥P-ABCD 中，底面ABCD 为直角梯形，∠ADC=∠BCD=90°，BC=1，PD=AD=2DC=2，∠PDA=60°，且平面PAD⊥平面ABCD。

（1）求证：BD⊥PC。

（2）在线段PA 上是否存在一点M，使二面角M-BC-D的大小为30°? 若存在，求出的值；若不存在，请说明理由。

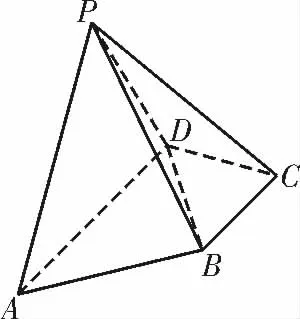
图4

5.（2020 年宿迁模拟）如图5，在正四棱柱 ABCDA1B1C1D1中，设AD=1，DD1=3，点P 在CC1上，且C1P=2PC。

（1）求直线A1P 与平面PDB 所成角的正弦值；

（2）求二面角A-BD-P 的余弦值。

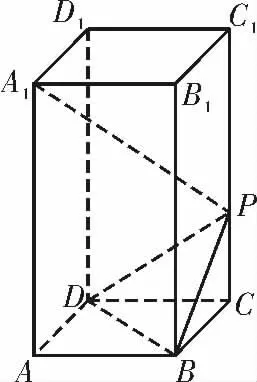
图5

6.（2020 年泉州模拟）如图6，已知四棱锥P-ABCD 的底面为菱形，∠BAD =120°，AB=2。平面PCD ⊥平面ABCD，PC=PD，E，F分别是BC，PD 的中点。

（1）求证：EF∥平面PAB；

（2）若直线PB 与平面ABCD 所成的角为45°，求直线DE 与平面PBC 所成角的正弦值。

图6

7.（2020 年蚌埠模拟）如图7，在四棱柱ABCD-A1B1C1D1中，AD ∥BC，AB ⊥AD，AD=AB=2BC，M 为A1D 的中点。

（1）证 明：CM ∥平面AA1B1B；

（2）若四边形AA1B1B 是菱形，且面AA1B1B⊥面ABCD，∠B1BA=60°，求二面角A1-CM-A 的余弦值。

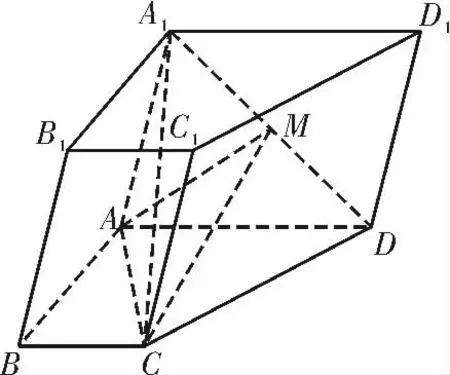
图7

8.（2020 年安徽模拟）如图8，在四棱锥P-ABCD 中，侧面PAB为等腰直角三角形，BC⊥平面PAB，PA=PB，AB=BC=2，AD=BD

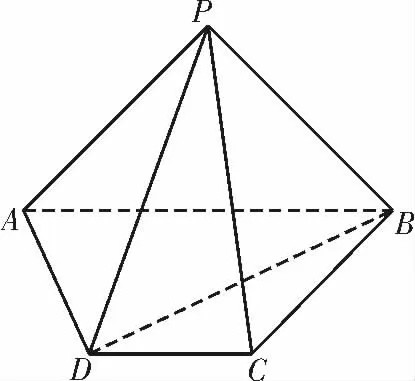
图8

（1）求证：PA⊥平面PBC；

（2）求直线PC 与平面PAD 所成角的正弦值。

9.（2020 年青岛模拟）如图9，在四棱锥E-ABCD 中，四边形ABCD 为平行四边形，△BCE 是边长为2的等边三角形，AB=AE，F，O 分别为AB，BE 的中点，OF 是异面直线AB 和OC 的公垂线。

（1）证明：平面ABE⊥平面BCE；

（2）记△CDE 的重心为G，求直线AG与平面ABCD 所成角的正弦值。

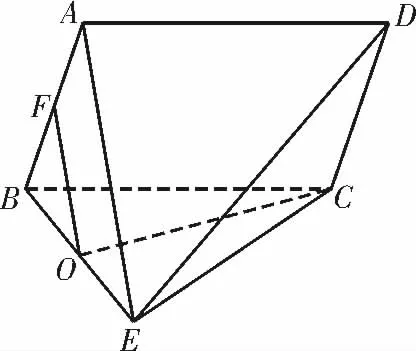
图9

10.（2020年大连模拟）如图10，在三棱柱ABC-A1B1C1中，侧面BB1C1C 为菱形，A 在侧面BB1C1C上的投影恰为B1C的中点O，E 为AB的中点。

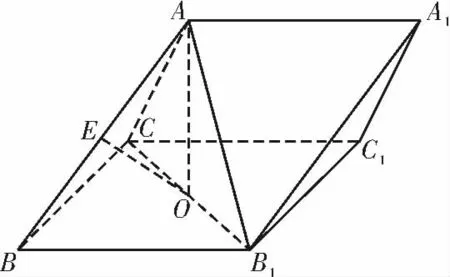
图10

（1）证 明：OE∥平面ACC1A1。（2）若∠CBB1=60°，cos∠ACC1=在线段C1A1上是否存在点F（F 不与C1，A1重合）使得直线EF 与平面ACC1A1所成角的正弦值为若存在，求出的值；若不存在，请说明理由。

参考答案：

1.（1）连接AC，由∠ABC=90°，AB=4，BC=3，得AC=

因为PA⊥平面ABCD，CD⊂平面ABCD，所以PA⊥CD。

因为PA∩AD=A，所以CD⊥平面PAD。

（2）以D 为坐标原点，AD 的延长线为x 轴，DC 为y 轴，过点D 与PA 平行的直线为z 轴，建立空间直角坐标系D-xyz，如图11所示。

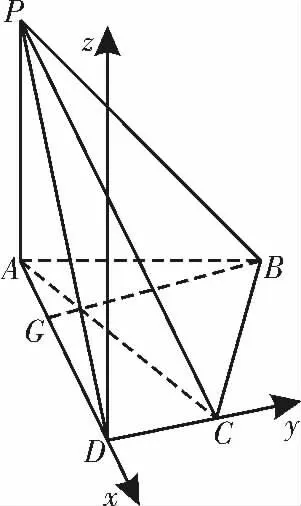
图11

因为平面PAC ⊥平面ABC，交线为AC，∠BAC=90°，故AB⊥平面APC，所以AB⊥PC。

又AP∩AB=A，所以PC⊥平面ABP。

又因为AD ⊂平面ABP，所以PC ⊥AD。

（2）因为平面PAC⊥平面ABC，在平面PAC 中过A 点作AC 的垂线l，则l 垂直平面ABC。

以A 为坐标原点，l 为z 轴，AB，AC所在直线分别为x 轴，y 轴，建立空间直角坐标系A-xyz，如图12所示。

在△APC 中，过点E 作EF⊥AC 于F，由CE=2EP 知E 为PC 的三等分点，易得E（0，6，2），B（6，0，0），C（0，12，0），A（0，0，0），所以=（0，6，

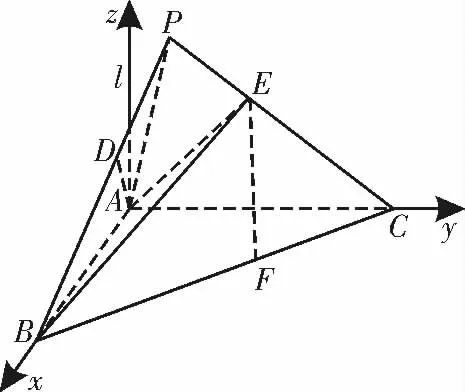
图12

设平面EAB 的 法向 量为m=（x1，y1，z1），则令y1=-1，得z1=，所以m=（0，-1，）。

设平面EBC 的法向量 为n=（x2，y2，z2），则令y2=1，得z2=，x2=2，所以n=（2，1，）。

3.（1）设点D 在平面ABC 上的射影为点E，连接DE，如图13，则DE⊥平面ABC。

因为BC⊂平面ABC，所以DE⊥BC。

因为四边形ABCD 是矩形，所以AB⊥BC，所以BC⊥平面ABD，所以BC⊥AD。

又AD⊥CD，CD⊂平面BCD，BC⊂平面BCD，CD∩BC=C，所以AD⊥平面BCD。

因为AD ⊂平面ABD，所以平面ABD⊥平面BCD。

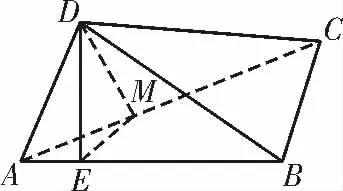
图13

（2）以B 为坐标原点，BC，BA 所在直线分别为x 轴，y 轴，建 立 空间直角坐标系B-xyz，如图14所示。

设AD=a，则AB=2a，所以A（0，2a，0），C（a，0，0）。

图14

又因为平面ABC 的一个法向量为n=（0，0，1），所以即二面角D-AC-B 的余弦值为

4.（1）如图15，过点P 在面PAD 内作PO⊥AD，垂足为O，连接BO，OC。

因为平面PAD⊥平面ABCD，所以PO⊥平面ABCD，所以PO⊥BD。

因为∠PDA=60°，PD=DA=2，所以△PDA 是等边三角形，所以OD=1=BC。

又因为OD∥BC，∠BCD=90°，所以四边形OBCD 是正方形，所以BD⊥OC。

又OC ∩PO=O，所以BD⊥平面POC。

又PC⊂平面POC，所以BD⊥PC。

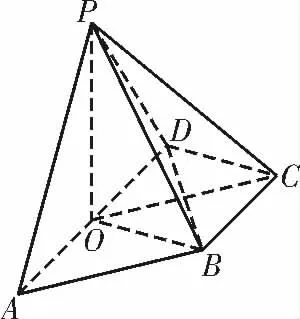
图15

（2）由（1）知PO⊥平面ABCD，OB⊥AD，所以以O为坐标原点，OA，OB，OP 所在直线分别为x 轴，y 轴，z轴，建立如图16所示的空间直角坐标系O-xyz 则B（0，1，0），C（-1，1，0），D（-1，0，0），P（0，0，），A（1，0，0）。

图16

假设在线段PA 上存在一点M，使二面角M-BC-D 大小为30°。

又平面ABCD 的一个法向量为n=（0，0，1），二面角M-BC-D 的大小为30°，所以化简整理得9λ2-18λ+8=0，解得（舍去），所以在线段PA 上存在点M满足题设条件且

图17

5.（1）如图17，以D 为坐标原点，DA，DC，DD1所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系D-xyz，则D（0，0，0），B（1，1，0），A1（1，0，3），P（0，1，1），所 以

设平面PDB 的法向量为n1=（x，y，z），则令x=1，得y=-1，z=1，所以n1=（1，-1，1）。

设直线A1P 与平面PDB 所成角为θ，所以

所以直线A1P 与平面PDB 所成角的正弦值为

（2）由（1）知平面PDB 的一个法向量为n1=（1，-1，1），取平面ABD 的一个法向量为n2=（0，0，1）。

6.（1）如图18，取PA 的中点 M，连接BM，MF。

因为M，F 分别是PA，PD 的中点，所以MF∥AD，且

图18

在菱形ABCD 中，E 是BC的中点，所以BE∥AD，且，所以MF∥BE，且MF=BE，所以四边形MBEF 是平行四边形，所以EF∥BM。又EF平面PAB，BM ⊂平面PAB，所以EF∥平面PAB。

（2）取CD 的中点为O，连接PO，AO，AC，因为PC=PD，所以PO⊥CD。

因为平面PCD ⊥平面ABCD，平面PCD∩平面ABCD=CD，PO⊂平面PCD，所以PO⊥平面ABCD，则∠PBO 为PB 与平面ABCD 所成的角，即∠PBO=45°。

在△BCO 中，BC=2，CO=1，∠BCO=120°，所以BO2=22+12-2×1×2×cos120°=7，所以BO=。

图19

如图19，以O 为坐标原点，OA，OC，OP 所在直线分别为x 轴，y轴，z 轴，建立空间直角坐标系O-xyz，则C（0，1，0），P（0，0，），D（0，-1，0），B（，

7.（1）取AA1的中点为N，连接MN，BN，因为M 为A1D 的中点，所以MN ∥AD，且MN=AD。又BC∥AD，BC=，所以MN∥BC，且MN=BC，所以四边形MNBC 是平行四边形，从而CM∥BN。又BN ⊂ 平面 AA1B1B，CM平面AA1B1B，所以CM∥平面AA1B1B。

（2）取A1B1的中点P，连接AP，AB1，因为四边形AA1B1B 为菱形，又∠B1BA=60°，易知AP ⊥AB。又平面AA1B1B ⊥平面ABCD，平面AA1B1B ∩平面ABCD=AB，AD⊥AB，所以AD ⊥平面AA1B1B，AD ⊥AP，故AB，AD，AP 两两垂直。

以A 为坐标原点，AB，AD，AP 所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系A-xyz，如图20 所示。不妨设 AB =4，则A（0，0，0），D（0，4，0），C（4，2，0），A1（-2，0，所 以

图20

设平面A1CM 的法向量为m=（x1，y1，z1），则

令x1=1，得y1=2，所以m =

设平面ACM 的法向量为n=（x2，y2，z2），则令x2=1，得y2= -2，所以n=

8.（1）因为BC⊥平面PAB，PA⊂平面PAB，所以BC⊥PA。因为△PAB 为等腰直角三角形，所以PA⊥PB。又PB∩BC=B，所以PA⊥平面PAB。

（2）取AB 的中点为O，连接OP，OD。因为PA=PB，AD=BD，所以PO⊥AB，DO⊥AB。因为BC⊥平面PAB，所以平面PAB⊥平面ABCD，所以PO⊥平面ABCD。因为OD⊂平面ABCD，所以PO⊥OD。

图21

如图21，以O 为坐标原点，OD，OB，OP 所在直线分别为x轴，y 轴，z 轴，建立空间直角坐标系O-xyz，则AO=BO=PO=1，又BC⊥AB，DO⊥AB，所以OD∥BC 且OD=BC，于是P（0，0，1），A（0，-1，0），D（2，0，0），C（2，1，0），所以（2，1，0）。

9.（1）因为O 为BE 的中点，所以在等边△BCE 中，OC⊥BE。又因为OF 是异面直线AB 和OC 的公垂线，所以OC⊥OF。又因为OF∩BE=O，OF，BE⊂平面ABE，所以OC⊥平面ABE。因为OC⊂平面BCE，所以平面ABE⊥平面BCE。

（2）因为F，O 为AB，BE 的中点，所以OF∥AE。又因为OF 是异面直线AB 和OC 的公垂线，所以OF⊥AB，所以AE⊥AB。又因为AE=AB，所以△ABE 为等腰直角三角形。

因为OA ⊥BE，OA ⊂平面ABE，平面ABE⊥平面BCE，且平面ABE∩平面BCE=BE，所以OA⊥平面BCE。

如图22，以O 为坐标原 点，OE，OC，OA 所在直线分别为x 轴，y轴，z 轴，建立空间直角坐标系O-xyz，则A（0，0，1），B（-1，0，0），C（0，

图22

因为四边形ABCD 为平行四边形，设D（x0，y0，z0），因为所 以（1，，0）=（x0，y0，z0-1），所以D（1，，1）。

10.（1）连接BC1，AC1。因为O，E 分别为BC1，AB 的中点，所以OE∥AC1。因为OE平面ACC1A1，AC1⊂平面ACC1A1，所以OE∥平面ACC1A1。

（2）由题意可知AO ⊥平面BB1C1C，四边形BB1C1C 为菱形，如图23，建立空间直角坐标系O-xyz。 设 BC=2，因为∠CBB1=60°，cos ∠ACC1=cos∠ACO·cos∠OCC1，所以cos∠ACO=所以AO=1，所以B，0，0），C（0，-1，0），C1（-，0，0），A （0，0，1），

图23

设平面AA1CC1的法向量为n=（x，y，z），因为所以令x=1，得

因为直线EF 与平面ACC1A1所成角的正弦值为或λ=0（舍去），所以