■江苏省锡山高级中学 戴静君

近几年高考的一个变化趋势，从知识立意到能力立意，再到如今的素养立意，对同学们的素质要求日益提升。比如，以前立体几何部分求二面角的大小是一个常见考点，考查的侧重点是通过建立空间直角坐标系利用两个平面的法向量的夹角与二面角的平面角之间的关系来求解，称为向量法。向量法思维要求较低，但对运算素养要求较高。新高考则更关注考查同学们的逻辑思维能力和逻辑推理能力，对二面角的求法提出了新的要求，即会用几何法求二面角的大小，突出了对同学们思维的灵活性和策略选择的要求。在此新的背景下，本文通过对几个例题的解析，提供多维度探究二面角的几种求法，为2021届高三数学立体几何复习备考提供一个参考。

一、几何法

几何法一般要求添加一些辅助线，对同学们的逻辑推理能力和空间想象能力要求较高，它的优点是运算相对简单，一旦找到二面角的平面角，往往能迅速且准确地得到结果，从而赢得时间。

1.定义法

例1（2020年全国Ⅲ卷理）如图1，在长方体 ABCD-A1B1C1D1中，E，F 分别在棱DD1，BB1上，且2DE =ED1，BF =2FB1。

（1）证明：点C1在平面AEF 内；

（2）若AB=2，AD=1，AA1=3，求二面角A-EF-A1的正弦值。

解析：（1）只需证四边形AFC1E 为平行四边形即可。过程略。

（2）如图2，取EF 的中点为N，连接A1N。过N 作AE 的平行线交AF 于点P，连接A1P。

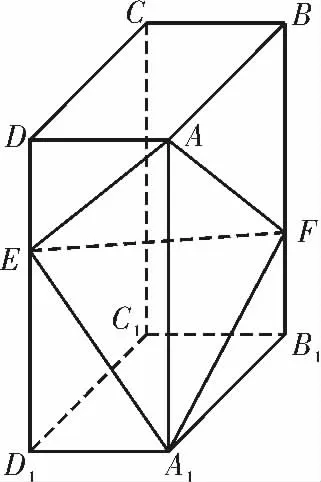
图1

在长方体 ABCDA1B1C1D1中，AD ⊥平面CDD1C1， DE ⊂ 平面CDD1C1，所以AD ⊥DE，故。同理求得，AF=，A1E=A1F=。

在直角梯形B1D1EF中，得EF =。

图2

在△AEF 中，AF2=8=AE2+EF2，所以AE⊥EF。

又AE∥NP，所以NP⊥FE。

因为N 是EF 的中点，A1E=A1F，所以A1N ⊥EF，所以 ∠PNA1是二面角A-EF-A1的平面角。

在等腰三角形 A1EF 中，A1N =

在△AA1F 中，cos∠A1AF=cos45°=得A1P2=5。

在△A1NP 中，利用余弦定理可得

所以二面角A-EF-A1的正弦值为

点评：上述解答过程直接利用垂直关系和等腰三角形A1EF 找到二面角的棱的垂线，通过平移和二面角平面角的定义直接找到二面角的平面角，然后解三角形即可。在此过程中一般要添加辅助线，注意图形中能产生垂直关系的条件，当线段长度关系较多时，试着用匀股定理的逆定理等进行解答。

2.垂线法

例2（2020年山东潍坊模拟）如图3，在四棱锥P-ABCD 中，AB=3，AP =，AD∥BC，AD ⊥平面PAB，∠APB=90°，点E 满足

图3

（1）证明：PE⊥DC。

（2）求二面角A-PDE 的余弦值。

解析：（1）因为AD ⊥平面PAB，且PE⊂平面PAB，所以AD⊥PE。

因为CD⊂平面ABCD，所以CD⊥PE。

（2）如图4，过E 作EF⊥AP 于F，EM ⊥PD 于M，连接FM。

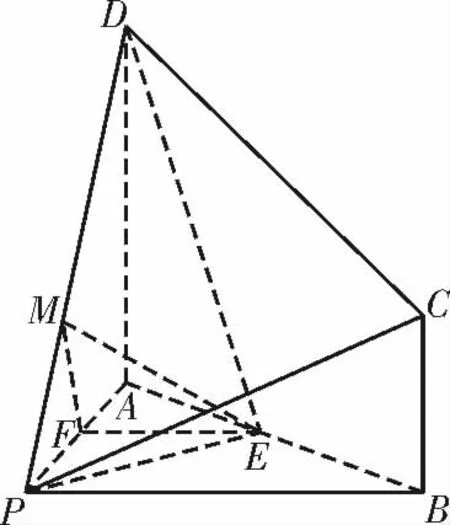
图4

因 为 AD ⊥ 平 面PAB，且EF⊂平面PAB，所以AD⊥EF。又EF⊥AP，所以EF⊥平面PAD。

因为PD⊂平面PAD，所以PD⊥EF，所以PD⊥平面EFM。

因为FM ⊂平面EFM，所以PD⊥FM。

所以∠EMF 是二面角A-PD-E 的平面角。

点评：上述解答过程推广到一般，就是在二面角的一个面内找一点P，过点P 找或作另一个面的垂线PH，再过点P 作棱的垂线PM，连接MH，则可证∠PMH 就是二面角的平面角。这种解法的关键是找或作平面的垂线。若条件中出现面面垂直，常利用此条件转化为线面垂直。有时线面垂直时垂足位置不好找，可以不管其具体位置，先作出二面角的平面角，然后利用体积转化法求出高即可求出二面角的平面角。

3.射影面积法

例3（2020年武汉模拟）如图5所示，多面体是由以四边形ABCD 为底面的直四棱柱被截面AEFG 所截而得到的，该直四棱柱的底面为菱形，其中AB=2，CF=5，BE=1，∠BAD=60°。

（1）求BG 的长；

（2）求平面AEFG 与底面ABCD 所 成锐二面角的余弦值。

解析：（1）BG 的长为。过程略。

图5

（2）因为多面体是由以四边形ABCD 为底面的直四棱柱被截面AEFG 所截而得到，所以GD ⊥平面ABCD，FC⊥平面ABCD，EB⊥平面ABCD，则四边形AEFG 在平面ABCD 上的射影就是四边形ABCD，由直四棱柱被 截面AEFG 所截，平面AEB ∥平面CDGF，又平面AEB∩平面AEFG=AE，平面CDGF∩平面AEFG=GF，所以AE∥GF。

点评：当一个封闭图形在另一个面上的射影易找时，可以直接利用射影面积公式求二面角的平面角的大小。特别地，当题中要求的二面角是无棱二面角时，有时棱很难找出，这时用此法显得尤为简单。

二、向量法

利用向量方法研究问题的途径主要是坐标思想和基底思想，当给出图形易于建系时，我们常常可以考虑用坐标法来求，但有时给出图形不便建系时还可以用基底思想求解。这种方法更侧重于代数运算，考查了运算基本素养。

例4（2020年山东淄博模拟）如图6，在四棱柱 ABCDA1B1C1D1中，已知底面ABCD 为等腰梯形，AB ∥CD，CDM，N 分别是棱AB，B1C1的中点。

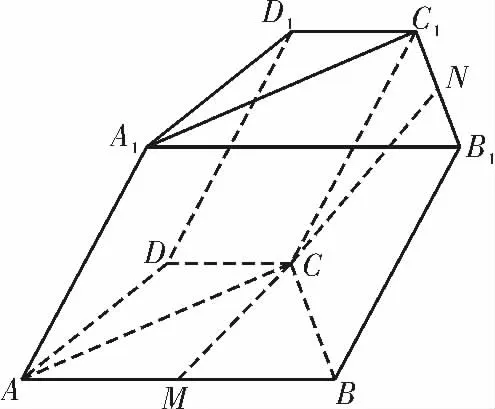
图6

（1）证明：直线MN∥平面ACC1A1；

（2）若D1C⊥平面ABCD，且求经过点A1，M，N 的平面A1MN 与平面ACC1A1所成二面角的正弦值。

解析：（1）证明略。

（2）连接CM，由已知得，MB=BC=CM，故△MBC 为等边三角形，所以∠ABC=60°，∠BAC=30°，所 以∠ACB=90°，即BC ⊥AC，所 以

据已知可以建立如图7 所示的空间直角坐标系C-xyz。

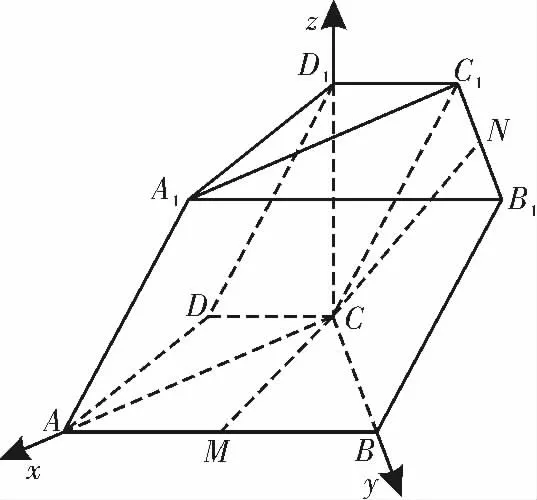
图7

点评：上述解题过程首先要找到两两垂直的三条直线建立适当的坐标系，一般让图形中尽可能多的点落在坐标轴上，这样便于写出点的坐标，减少无谓的失误。一般情况下，当条件给出的图形有明显的线面垂直关系，或给出面面垂直的条件可以转化为线面垂直时，往往可以直接建立坐标系，利用坐标法求解。

二面角的平面角解法的多样性能充分考查同学们的综合解题能力。近年来的高考试题，寓基础性、综合性、应用性、探索性、灵活性于一体，需要我们在知识与方法的整合中全方位地提升基本数学素养，理性地思考，智慧地做题。