徐 超，单志勇，2，徐好好

（1.东华大学信息科学与技术学院；2.数字化纺织服装技术教育部工程研究中心，上海 201620）

0 引言

粒子群优化（Particle Swarm Optimization，PSO）算法1995 年由Kennedy 等［1］提出。粒子群算法由于原理简单、容易实现等优点，在实际工程中得到广泛应用［2-4］，但是粒子群算法对于高维函数问题往往不能收敛到全局最优点，收敛精度不高。针对这些问题，研究人员引进多种理论改进粒子群算法，集中在算法本身改进和与其它算法混合两个方面［5-7］。文献［8］提出一种具有指数衰减惯性权重的粒子群优化算法，改进后的算法收敛精度和收敛速度都得到提升；文献［9］利用余弦函数调整惯性权重与学习因子，增强粒子进化的多样性；文献［10］将引力搜索算法与动态多种群粒子群算法相结合，通过邻域进化策略提高粒子全局搜索能力；Ghasemi 等［11］将学习因子与算法迭代次数线性组合，给予粒子跳跃的学习能力，增强粒子跳出局部极值的能力；刘军梅［12］通过混沌效应，使种群数量随优化过程变多，保护种群多样性；文献［13］提出一种层次学习粒子群优化算法，算法进化过程中保留最高层粒子，避免种群多样性丧失，提高算法的全局收敛能力；Cheng 等［14］将粒子按照适应度值进行排序，根据粒子排序的不同调整粒子学习能力，算法在高维函数问题上具有良好的寻优性能。

本文结合文献［13］的层次学习思想与文献［14］的动态学习能力策略，对文献［13］全局收敛能力不足和文献［14］收敛速度慢的问题进行改进，提出一种具有动态学习能力的分层进化粒子群优化算法。首先将粒子按照适应度值排序，根据其适应度值将粒子分为多个层次；然后对不同层次的粒子选择不同的进化策略，同时根据粒子在整个种群中排序的不同动态调整粒子的学习能力，使高层级粒子具有精确的搜索能力，低层级粒子具有较高的空间探索能力，在保证算法全局收敛能力的同时提高算法收敛速度；最后将本文提出的算法与标准粒子群算法（PSO）、惯性权重线性递减粒子群算法（LDWPSO）、余弦学习因子粒子群算法（IPSO）与可扩展的社会学习粒子群算法（SLPSO）进行对比实验，证实本文算法性能。

1 基本粒子群优化算法

随机产生含有N 个粒子的种群，每个粒子都是D 维向量，用xi=[xi1,xi2,…,xiD]表示，第i个粒子对应的速度也为D 维向量，用vi=[vi1,vi2,…,viD]表示，其中i=1,2,…,N，粒子更新公式如下：

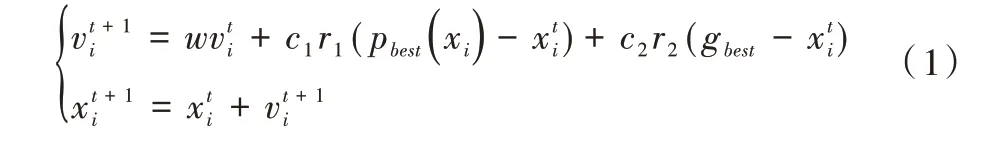
其中：w为惯性权重，c1、c2为学习因子，r1、r2为[0,1]之间的随机数，pbest(xi)表示第i个粒子自身经历过的最优位置，gbest表示整个种群经历过的最优位置。每个粒子通过不断进化pbest和gbest来更新自身的速度与位置，从而寻找到优化问题的最优解［15-17］。

2 改进的粒子群算法

2.1 算法原理

2.1.1 排序分层与学习策略

在进化过程中，粒子通常处于不同演化状态，不同的粒子学习能力也不同。为了区分粒子，根据适应度值将粒子划分为不同层次。假设NP个粒子被划分为NL个层级，每个层级NL以Li表示（1≤i≤NL）。在分层之前粒子首先按照适应度降序排序，较好的粒子属于较高层级，层级指数也较大，L1是最低层，LNL是最高层。每层所含有的粒子数量大小由LS表示，很明显，LS=NP/NL。假设粒子在整个种群中排名为m，粒子层级指数i与m的关系如下：

排序分层与学习策略如图1 所示。

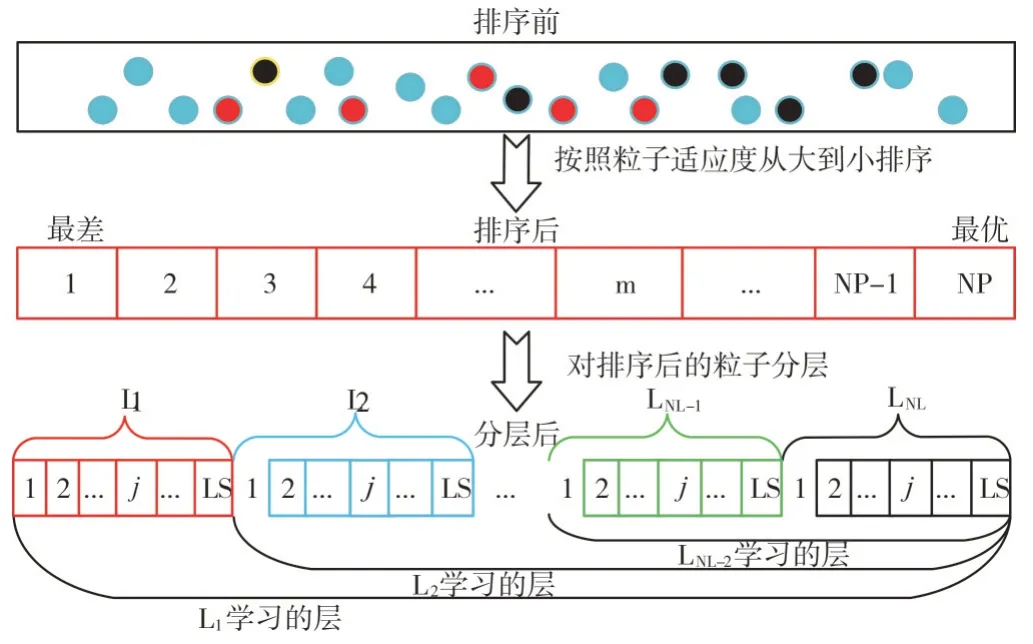
Fig.1 DHEPSO layered algorithm图1 DHEPSO 算法分层

2.1.2 进化策略

为避免种群在迭代过程中过早丧失多样性，同时保证算法收敛速度，本文对L1～LNL-2、LNL-1、LNL三个不同范围层次的粒子采取不同的学习与进化策略。进化策略如下：

（1）L1～LNL-2层的粒子更新公式如下：

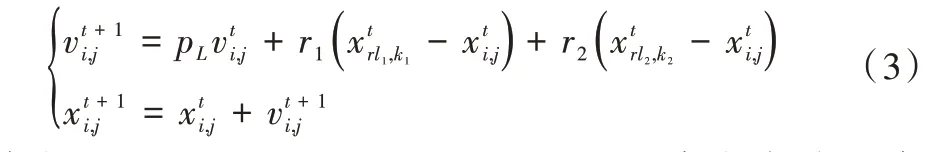
其中：i=1,2,…,NL-2；j=1,2,…LS；t代表当前迭代次数，表示第i层的第j个粒子，表示第rl1层的第K1个粒子，表示第rl2层的第K2个粒子，K1、K2属于区间[1,LS]的随机整数。注意：rl1、rl2属于区间[i+1,NL]之间的随机整数，并且rl1≠rl2。

pL为粒子对应的学习能力，粒子学习能力与该粒子在整个种群中排名负相关。粒子学习能力计算公式如下：

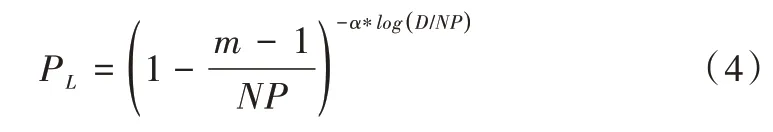
其中，D为粒子维数，m为将粒子适应度按照降序排列后该粒子在整个种群中的排名，α为控制学习因子，一般取α∈[0,1.5]。图2 为NP=100、D=50 时，pL随m和α的变化曲线。从图中可以看出，在种群数量固定，粒子维数相同情况下，粒子的学习能力随排名的增大递减，控制学习因子α越小，粒子的学习能力随排名的变化程度越大。

（2）LNL-1层的粒子向LNL层中两个不同的粒子学习，LNL-1层粒子更新公式如下：

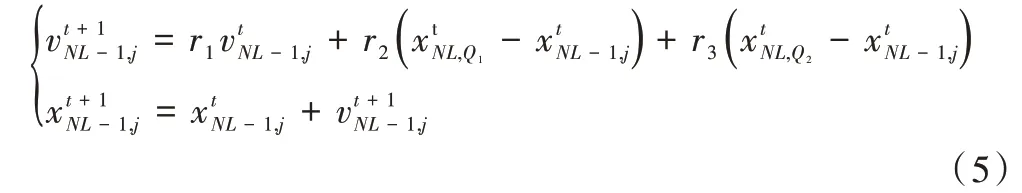
其中：r1，r2，r3为区间(0,1)内的随机数，表示LNL-1层的第j个粒子，为对应速度；代表LNL层中两个不同粒子。注意：Q1、Q2属于区间[1,LS]之间的随机整数，并且Q1≠Q2。

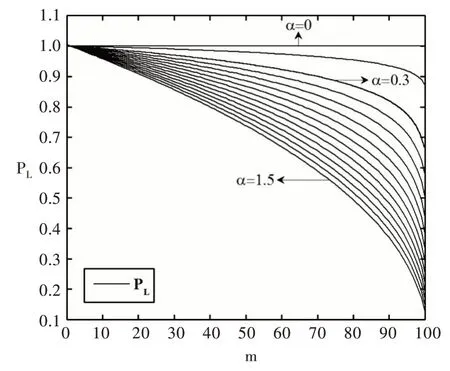
Fig.2 Particles learning curve图2 粒子学习能力变化曲线

（3）LNL层粒子在整个种群进化过程中起主导作用。为避免整个种群在进化过程中过度向全局最优粒子学习，导致种群多样性快速丧失，在升级最高层粒子时，保留最高层级中最优的两个粒子。LNL层粒子更新公式如下：

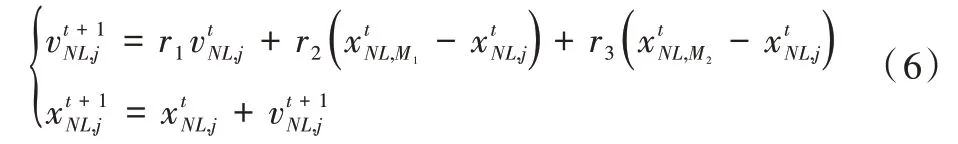
其中：r1，r2，r3为区间(0,1)内的随机数，代表第NL层中的第j个粒子，注意1≤j≤LS-2；代表LNL层中的两个不同粒子，M1、M2属于区间[j+1,LS]之间的随机整数，并且M1≠M2。

2.2 DHEPSO 算法步骤

DHEPSO 算法步骤如下：①初始化种群数量NP、层数NL、控制学习因子α、最大迭代次MAX_FES；②计算所有粒子适应度值，全局最优位置为x，f(x)为对应的适应度值；③将粒子按照适应度降序排列，同时记录粒子在种群中的排名m；④根据公式（4）求出粒子对应的学习能力pL；⑤根据m和公式（2）求出粒子对应的层级指数，将粒子划分进对应层级；⑥根据公式（3）升级L1到LNL-2层粒子，如果f(xi,j)＜f(x)，则令x=xi,j，f(x)=f(xi,j)；⑦根据公式（5）升级LNL-1层粒子，如果f(xNL-1,j)＜f(x)，则令x=xNL-1,j，f(x)=f(xNL-1,j)；⑧根据公式（6）升级LNL层粒子，如果f(xNL,j)＜f(x)，则令x=xNL,j，f(x)=f(xNL,j)；⑨更新全局最优位置x和全局极值f(x)；⑩如果达到最大迭代次数则算法终止，输出全局最优位置和全局极值，否则跳到步骤③。

3 仿真实验与结果分析

3.1 测试函数

为验证本文算法的正确性，选取4 个典型测试函数［18-20］进行仿真对比实验，测试函数公式与搜索范围如表1 所示。

3.2 实验设置

实验硬件环境为AMD A10-4600M,CPU 为2.40 GHz，内存为8 GB，在Matlab 2018a 下完成。

Table 1 4 typical test functions表1 4 个典型测试函数

为验证本文算法的有效性，选取PSO 算法、LDWPSO算法、IPSO 算法、SLPSO 算法与DHEPSO 算法进行仿真对比实验，各种算法独立运行30 次，统计粒子适应度的平均值与标准差。设置所有算法初始种群数量NP=100，最大迭代次数500 次，函数粒子维数分别取30 维和50 维。各算法的初始参数设置如表2 所示。

Table 2 Algorithm initial parameters settings表2 算法初始参数设置

3.3 结果分析

5 种算法在4 个测试函数上的标准差（Std）和适应度平均值（Mean）统计数据如表3 所示，实验最好结果用粗体表示。

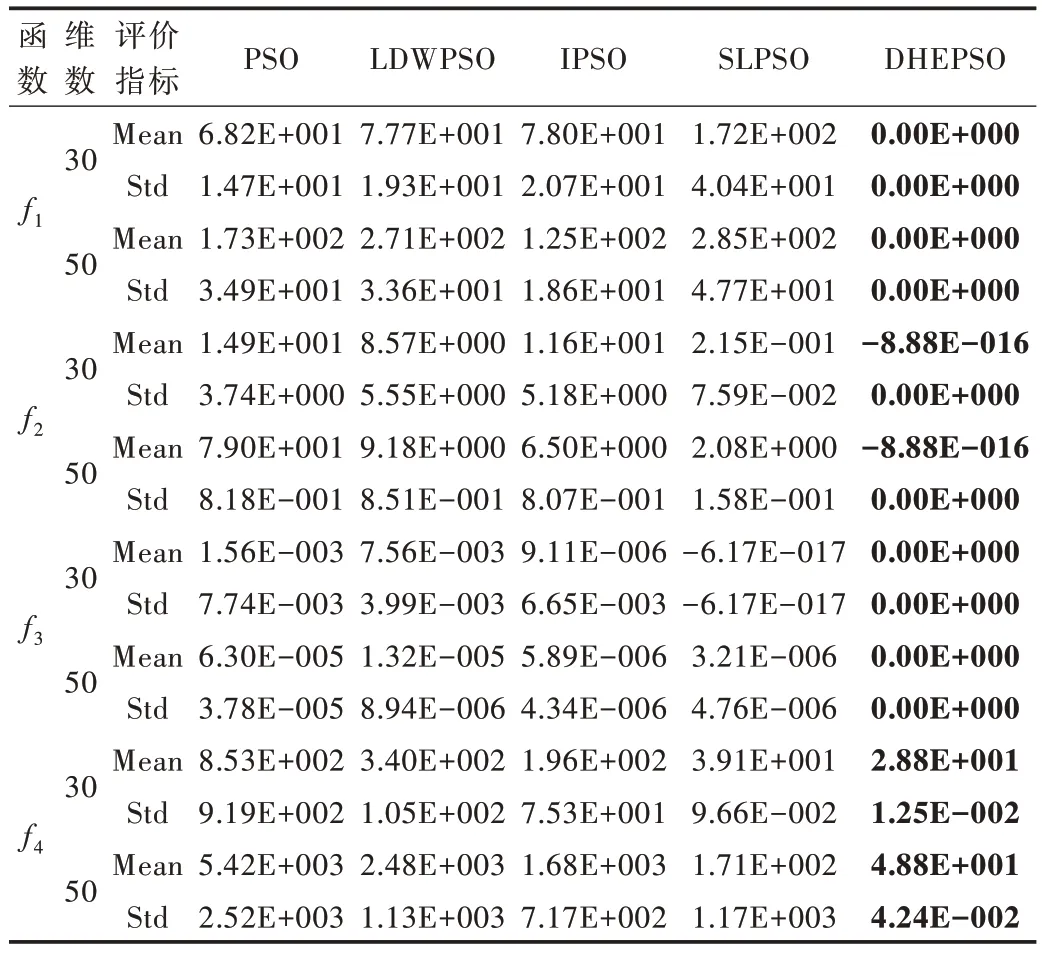
Table 3 5 kinds of PSO algorithm simulation results of four test function表3 5 种PSO 算法对4 个测试函数仿真结果

由表3 可以看出，对于所选的测试函数除f2和f4外，DHEPSO 算法在所规定的迭代次数内达到全局最优。DHEPSO 算法相对于基本PSO 算法和其它两种对比算法，在收敛精度和稳定性上都有很大优势。虽然f2和f4函数没有收敛到全局最优，但是由表中数据可以看出其它对比算法优化效果较差，并且对于f2函数，DHEPSO 算法的优化结果比其它算法低了14 个数量级。

为了更直观表现出算法的收敛情况和适应度变化情况，图3 给出在50 维时部分算法的适应度对比曲线，其中f1和f6函数的纵坐标是以10 为底取对数的结果。由图3中的适应度曲线可以看出，DHEPSO 算法在4 个测试函数中收敛速度最快，同时全局收敛能力最好。

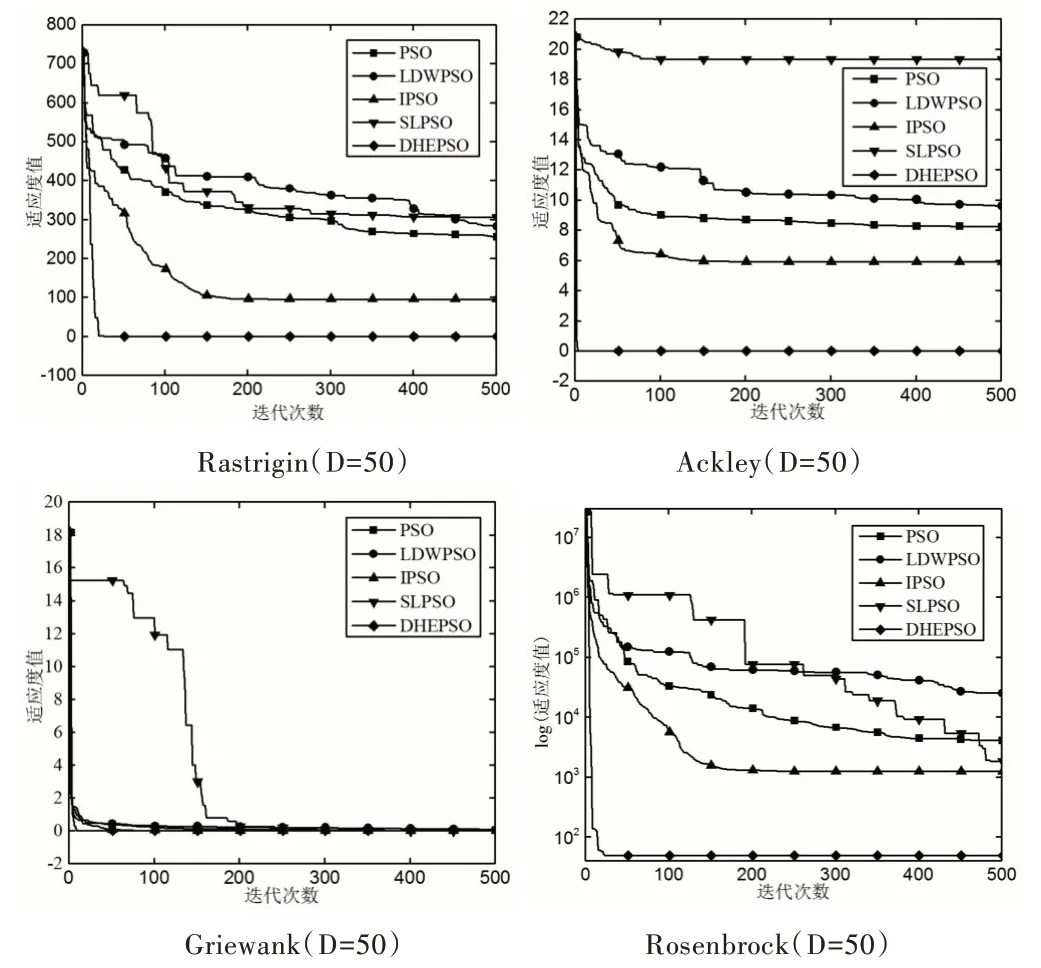
Fig.3 Algorithm fitness curves图3 算法适应度曲线

4 结语

本文在标准粒子群算法基础上提出一种具有动态学习能力的分层进化粒子群优化算法，结合分层进化策略与动态学习能力思想，避免迭代后期种群多样性丧失，有效提高了全局收敛能力，同时保证了算法收敛速度。在4 个典型测试函数上本文算法均取得良好成绩，证明本文算法具有良好的优化性能。但是算法在高维病态函数上性能提升较小，这是以后改进方向。通过对标准粒子群算法与其改进算法的深入研究可知，对粒子群算法初始种群、惯性权重、学习因子等方面进行合理改进，均可有效提升算法性能。