万 鹏，吕毅斌，王樱子，唐胜男

（1.昆明理工大学 理学院；2.昆明理工大学 计算中心，云南 昆明 650500）

0 引言

保角变换又称共形映射，是复变函数的重要内容，在很多领域扮演着重要角色，如流体力学、医学图像处理、电磁理论等［1-4］。然而，除了在少数特殊情况下可以解出保角变换的解析解外，大多数工程与科学问题中求解保角变换的解析非常复杂甚至无法求解，所以对数值保角变换研究成为科学工程领域必不可少的课题。目前比较著名的方法有Symm［5-6］提出的积分方程法，Dai［7-10］提出的基于模拟电荷法的数值保角变换计算法，Sangawi 等［11-12］提出的带有广义Neumann kernel 的边界积分法等。

共轭调和函数具有严谨的理论基础而且容易计算。模拟电荷法是Steinberger 计算电场时提出的方法，Amano 利用模拟电荷法将数值保角变换的近似问题转换为共轭调和函数的逼近问题。相较于Symm 提出的积分方程法和Nass⁃er 提出的带有广义Neumann kernel 的边界积分法，基于模拟电荷法的数值保角变换计算法避免了很多数值积分微分等计算操作，可降低数值保角变换计算的复杂度和时间。

模拟电荷点的位置及数量选取问题至今没有统一方法，很多情况下数值保角变换的最终结果对模拟电荷点位置及数量选取极为敏感，对于简单的较为规则的边界问题而言，如圆形或椭圆外部区域，Amano 提出的基于模拟电荷法的数值保角变换计算法具有较高精度，但是对于一些较为复杂的边界如橙形、心形等，基于模拟电荷法的数值保角变换误差会明显上升，所以基于模拟电荷法的数值保角变换计算法精度还有很大的改善空间。

本文对单连通橙形外部区域、单连通椭圆外部区域给出电荷点和约束点位置，使用基于（k，j）-Padé［13-14］迭代法改进的SSOR 方法［15-16］求解电荷量，以降低模拟电荷点数量选取对最终结果的影响，最后利用求得的电荷量计算出数值保角变换函数。在数值实验中针对不同电荷点数量进行多组实验，通过误差比较证明改进算法的精确性，并实现数字图像的保角变换。

1 相关知识

将z-plane上Jordan 闭曲线C1,C2,…,Cn外侧的无穷远点的非有界多连通区域D映射到ω-plane（含有竖直狭缝的平面）。如果z=0 在区域D内，在正则化条件f(∞)=∞，f'(∞)=1，a0=0 下，竖直角度的保角变换在无穷远点的Laurent 级数可唯一表示为如下形式：

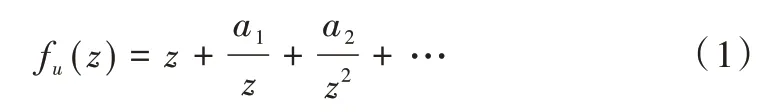
保角变换可将曲线C1,C2,…,Cn映射成竖直狭缝ω=fu(z)，fu(z)可以表示为：

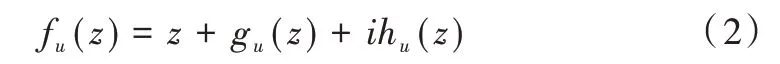
其中gv和hv是一对共轭调和函数。

（1）边界条件。

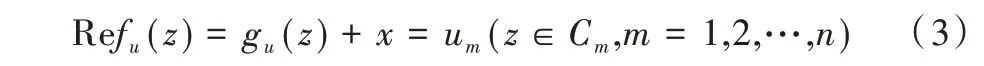
根据模拟电荷法，gu(z)+ihu(z)可逼近Gu(z)+iHu(z)，它可以表示为：

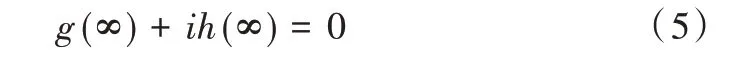
（3）约束条件。

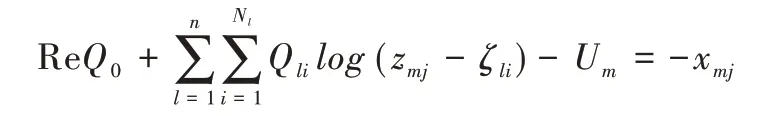
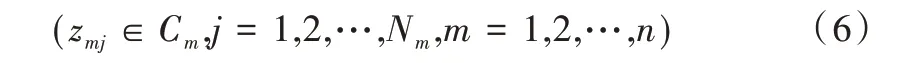
（4）正则化条件。

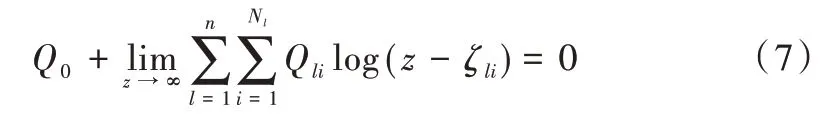
可得：

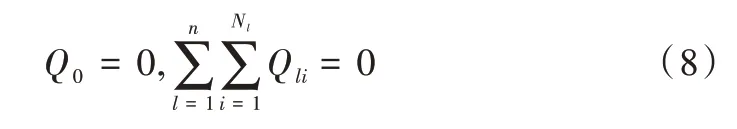
（5）柯西条件。复变函数（4）是区域D内的解析函数，D内的任意闭曲线设为，设为只包围Cl的封闭曲线：

故有：

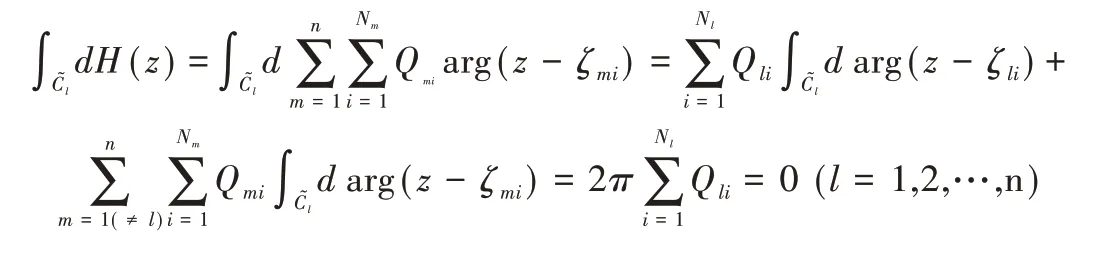
可得：

其中Nl为Cl内电荷点数量，ζli(i=1,2,…,Nl)是分布在曲线Cl外部区域D中的电荷点，zmj(j=1,2,…,Nm)为在边界Cm上的约束点，电荷量Qli由公式（10）和边界条件（3）以及电荷点和约束点决定，Um是狭缝位置，为um的近似值。式（6）计算出的电荷量和狭缝位置用来逼近fu，即：

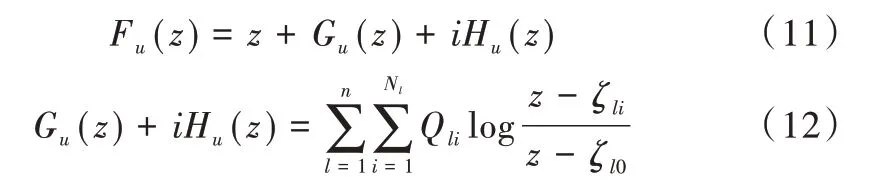
其中ζl0为Cl内的一点。

将式（12）进行变形得：

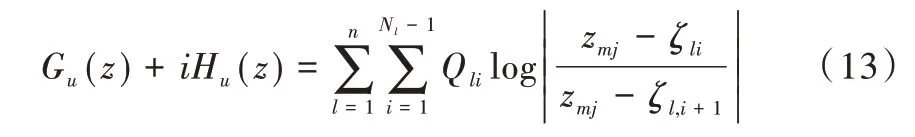
根据式（6）、式（10）和式（13），联立一次方程求电荷点以及狭缝位置U1,U2,…,Un：

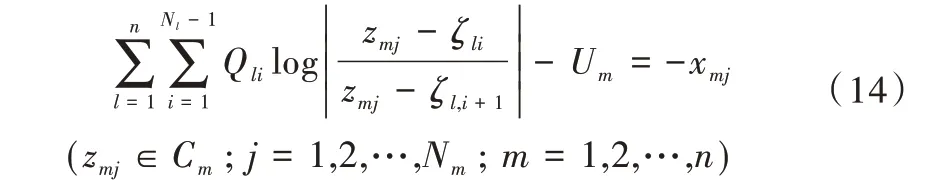
2 本文方法

上述约束方程将其写为标准线性方程：

改进的SSOR 迭代法［11-12］可以很好地改善其病态性。首先对式（1）两边分别乘以ωi AT：

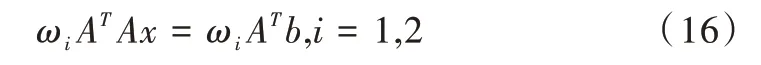
其中，AT A为对称正定矩阵，ωi∈(0,2),i=1,2 为松弛因子。根据参考文献［11］、［12］对ωi AT A进行分裂，ωi AT A=Mi-Ni,i=1,2，于是有：

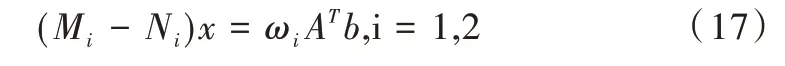
其中M1=D-ω1L，N1=(1-ω1)D+ω1U，M2=D-ω2U，N2=(1-ω2)D+ω2L，D=diag(a1,1,a2,2,…,aN,N)，L为负的严格下三角矩阵，U为负的严格上三角矩阵。

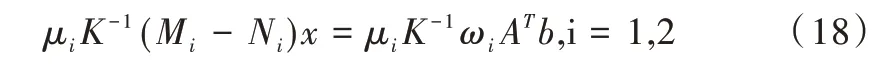
对式（17）两边乘以μiK-1，得：其中，K 为预条件算子，一般取K 为D=diag(a1,1,a2,2,…,aN,N)或单位矩阵，i=1 时，μi取，i=2 时，μi取，x值更接近准确值，λ1，λN+1分别为Mi-Ni的最大特征值、最小特征值。

由式（18）构造两个半步迭代公式：

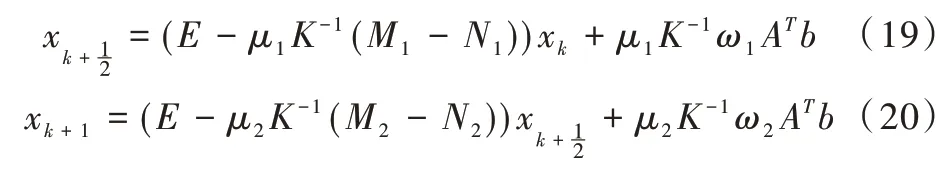
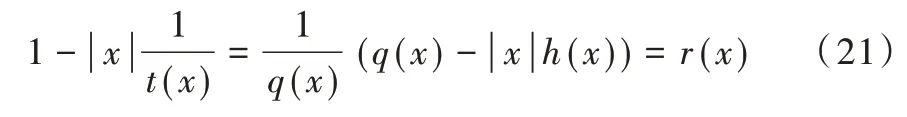
根据式（18）定义矩阵多项式r(-μi(Mi-Ni))=E-μiK-1(Mi-Ni)=ri，t(-μi(Mi-Ni))=ti，q(-μi(Mi-Ni))=qi，h(-μi(Mi-Ni))=hi，得到迭代的矩阵多项式：

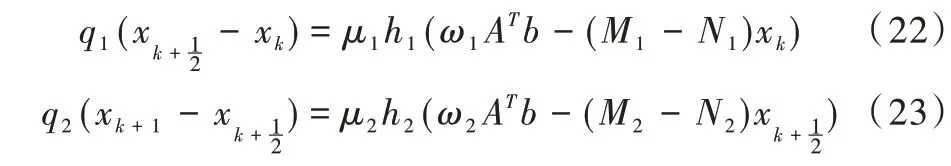
改进SSOR 方法收敛性如下：

证明：根据参考文献［3］，对任意的n≥m，x＜0，μi＞0，ωi＞0，rnm(x)＜1，由于AT A是正定的，故ωi AT A=Mi-Ni也是正定的，故Mi-Ni的特征值都大于0，则-μi(Mi-Ni)的特征值都小于0，则有：

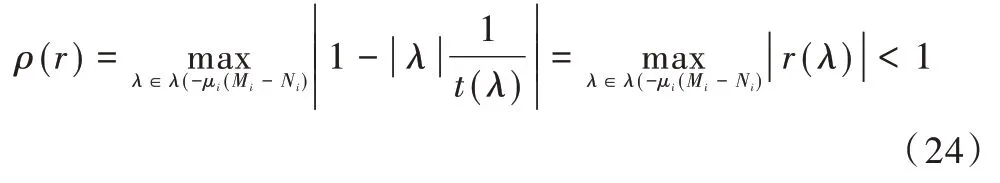
故改进的SSOR 迭代法基于（n，m）-Padé 迭代法收敛。

基于上述方法给出基于(k,j) -Pade'迭代法的SSOR相关算法。

算法流程如图1 所示。

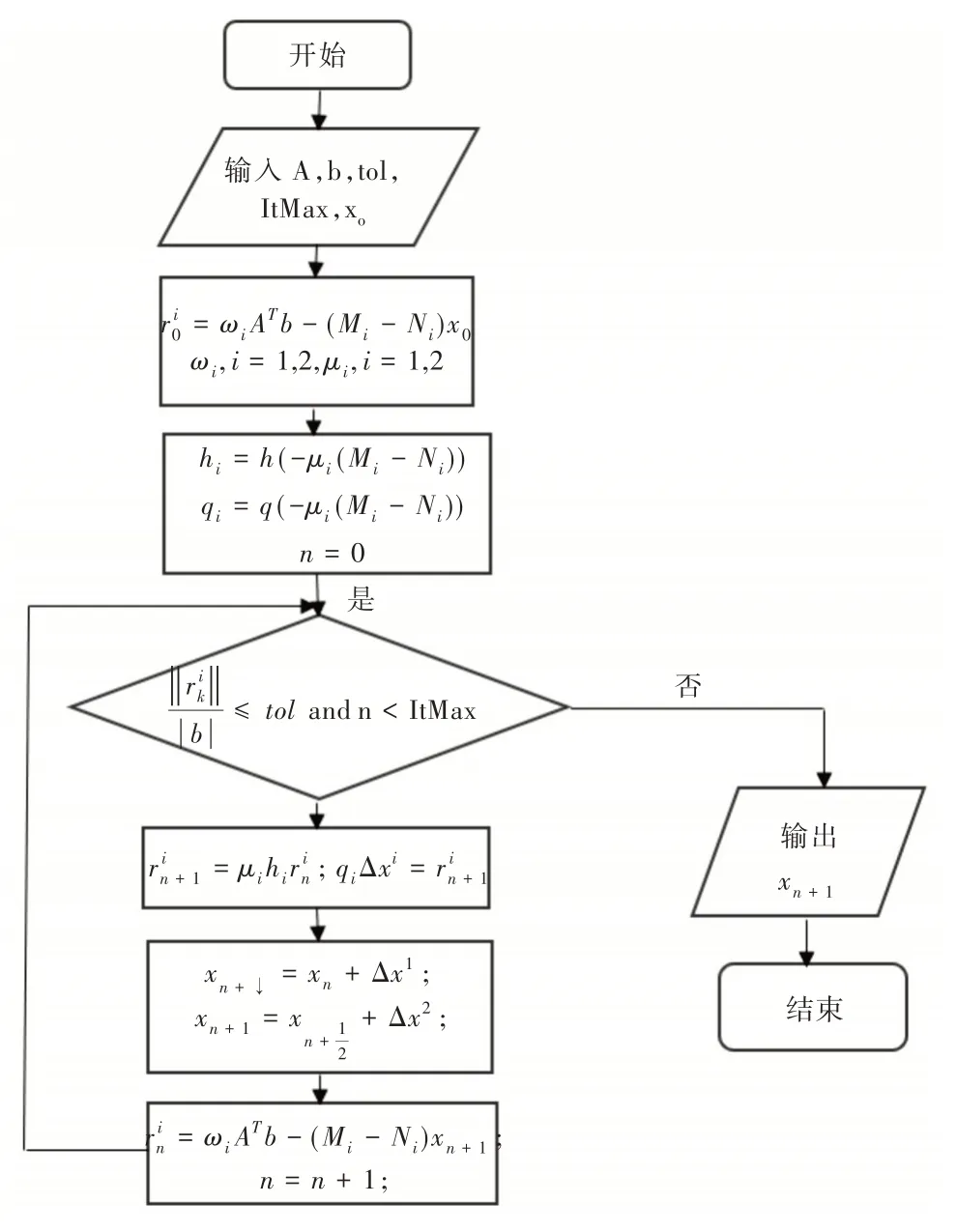
Fig.1 Based on the（n，m）-Padé SSOR algorithm of iterative process图1 基于（n，m）-Padé 迭代法的SSOR 算法流程

通过以上改进的SSOR 方法得到基于（n，m）-Padé 迭代法的数值保角变换步骤：①给出每条曲线C1,C2,…,Cn上电荷点的数量Nl(l=1,2…,n)，以及电荷点的坐标和约束点的坐标(m=1,2,…,n)；②根据公式（13）构造约束方程组；③利用改进的SSOR 法和迭代公式求解电荷量和狭缝位置；④由模拟电荷法求出保角变换的近似函数；⑤利用改进的数值保角变换计算法实现图像保角变换。

3 实验结果

在Windows10 系统上用Matlab 2016b 对以橙形为边界的单连通区域进行数值实验并分析实验结果，然后通过该方法实现图像的数值保角变换。根据复变函数中的最大模原理［18-19］得到误差和竖直狭缝位置的误差计算公式。

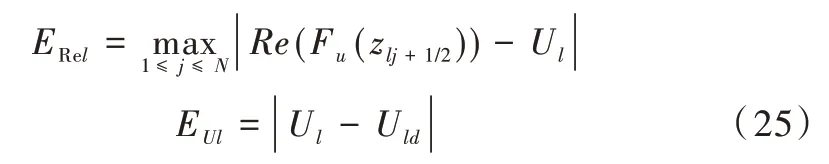
例1：当l=1 时的橙形外部区域

边界：

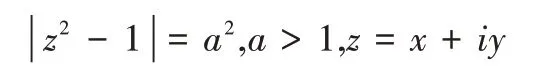
边界参数方程：

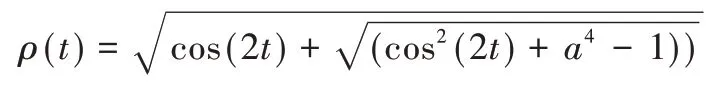
约束点：

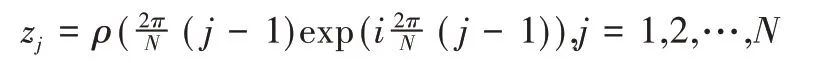
电荷点：

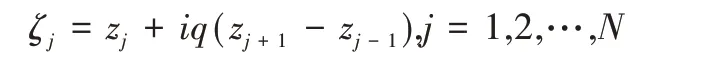
其中：z0=zN,zN+1=z1

图2 构造40×40 网格，图3 是橙形外部区域。约束点分布在边界上，电荷点在区域的内部，其中i是虚数单位，0＜q＜1，是调整电荷点位置的参数。

图3 是图2 用改进后的算法进行数值保角变换结果。从图中可以看出变换前后的角度关系，显示该算法的优越性。图中把橙形变成一条竖直的线，由图2 和图3 可以看到网格变换前后的变化。

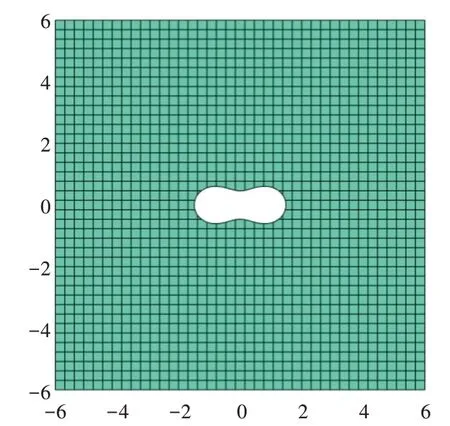
Fig.2 Problem areas（a）图2 问题区域

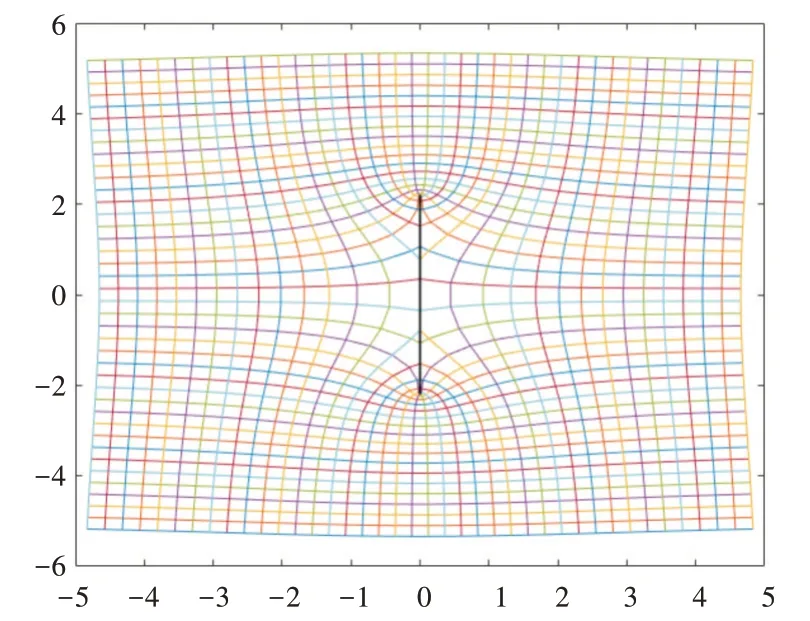
Fig.3 Fig.2 transformation results under the improved algorithm图3 图2 在改进算法下的变换结果

用式（20）作为误差指标，图4 和图5 为分别用Amano法、LQ 分解法、双共轭梯度法和本文方法求解电荷量，并计算出数值变换函数，最后画出变换函数的误差曲线。从图4 可以看出，随着电荷数量的增加，本文方法的误差一直在减小，而Amano 方法在数量较小的情况下误差明显增加，在超过一个特定范围之后又明显减小，但本文方法是一直在减小，而且和Amano 方法有很大差距。从实验数据计算可知，本文方法比原有方法精度平均提高0.101 9，最大提升率为11.2%，LQ 分解法和双共轭梯度法虽然在一定程度上比Amano 方法好，但是整体效果还是比改进算法要差一些。从图5 可以看到竖直狭缝位置之间的误差。Amano 方法的误差刚开始很大，然后突然减小，说明Ama⁃no 方法不稳定。虽然本文方法和Amano 方法从误差曲线上看差距不是很大，但本文方法误差刚开始时在减小，当电荷数量达到某个临界点时误差曲线会趋于平衡状态，说明本文方法更加稳定。从实验数据计算可知，本文方法比原有方法精度平均提高0.009 0，故通过图3 与图4 可以看出本文方法较Amano 方法更加稳定，且本文方法可改善方程组的病态性，对于求解病态的对称约束方程组有明显优势。LQ 分解法和双共轭梯度法相对本文算法而言不稳定，精度也略有欠缺。

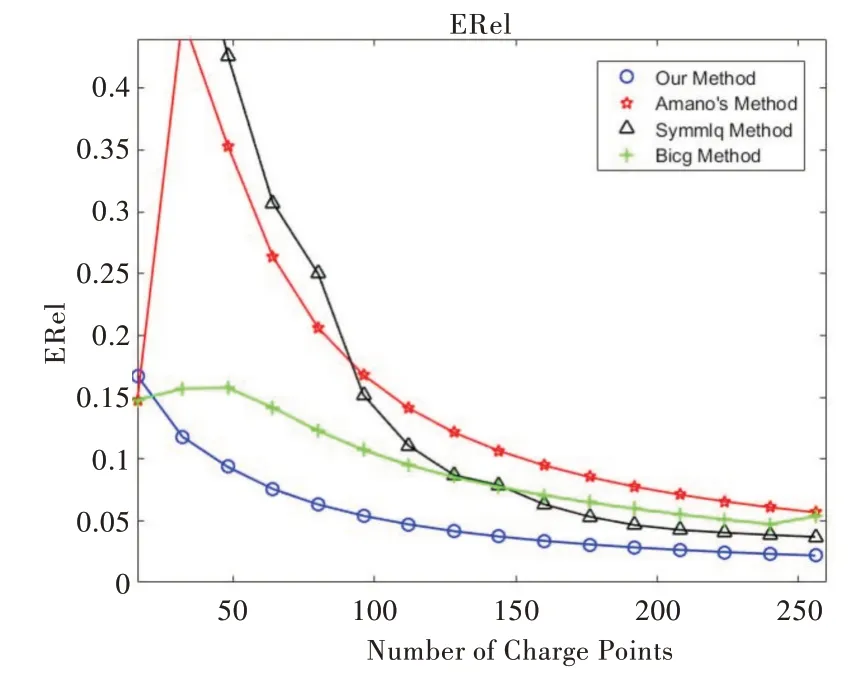
Fig.4 Erel（a）图4 Erel（a）

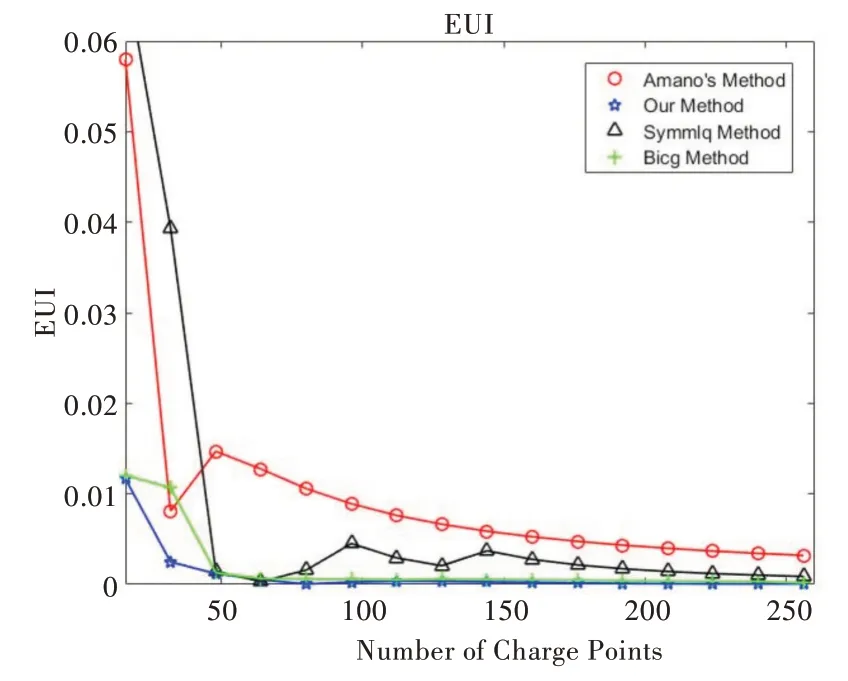
Fig.5 Vertical slit position error（a）图5 竖直狭缝位置误差

图6 是原始图像，图7 是图像变换结果。把橙形变成竖直狭缝得到图7 的变换结果。

Fig.6 Original image（a）图6 原始图像

Fig.7 Transform result of Fig.6图7 图6 的变换结果

例2：单联通椭圆外部区域

电荷点：

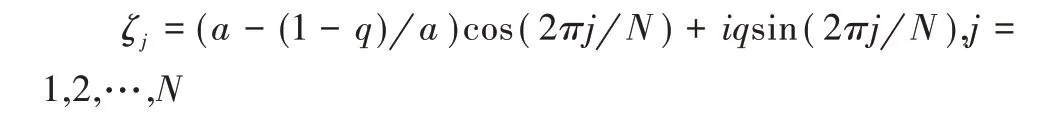
约束点：

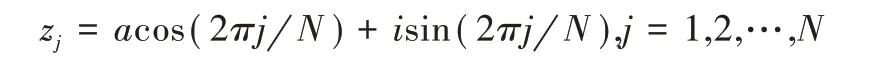
约束点分布在边界C 上，电荷点分布在边界C 内部，其中i是虚数，0 ＜q＜1 是控制电荷点的位置分布。

图8 是单联通椭圆外部区域，构造了40 × 40 的网格，图9 是图8 变换的结果，由保角变换把椭圆变成一条竖直狭缝，网格也发生一系列畸变，反映保角变换前后的角度变化，这些角度变化很好地表现出该算法的优势。

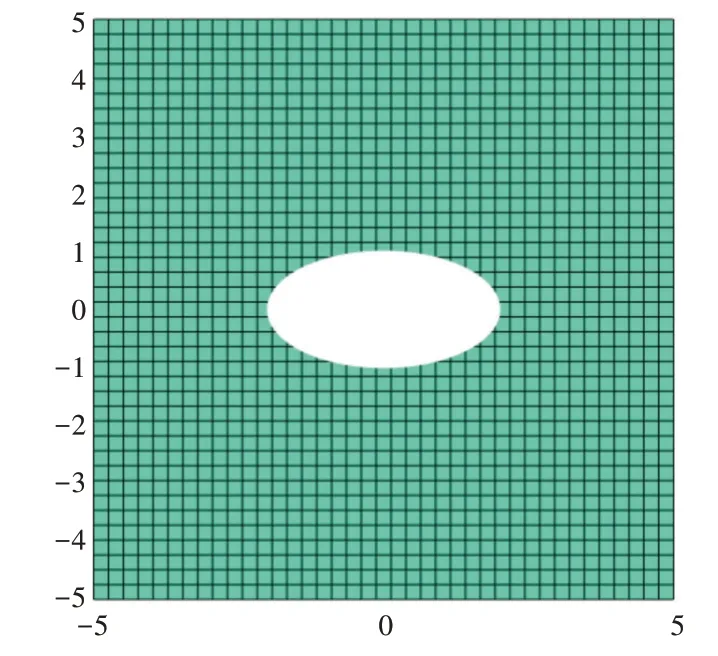
Fig.8 Problem areas（b）图8 问题区域

图10 和图11 表示在公式（20）下根据两种误差评判指标画出的误差曲线图，图10 和图11 画出了本文方法和Amano 方法的误差曲线。从图10 可以明显看出本文方法和Amano 方法的误差曲线，随着电荷数量的增加误差都在减小，但本文方法和Amano 方法的误差曲线还是存在区别。从实验数据计算得到本文方法比原有方法精度平均提高约0.026 4，最大提升率为5.4%，而LQ 分解法和双共轭梯度法在简单边界上的变换效果比原有Amano 方法要差一些。图11 中虽然两者曲线差距不太明显，精度平均提升0.002 4，但是本文方法震动弧度不是很大，比原有方法更为稳定。而LQ 分解法和双共轭梯度法不稳定，误差一直在上下波动，所以本文方法体现出稳定性好的特点。因此，本文方法不仅稳定性好而且精度高，优势更强。

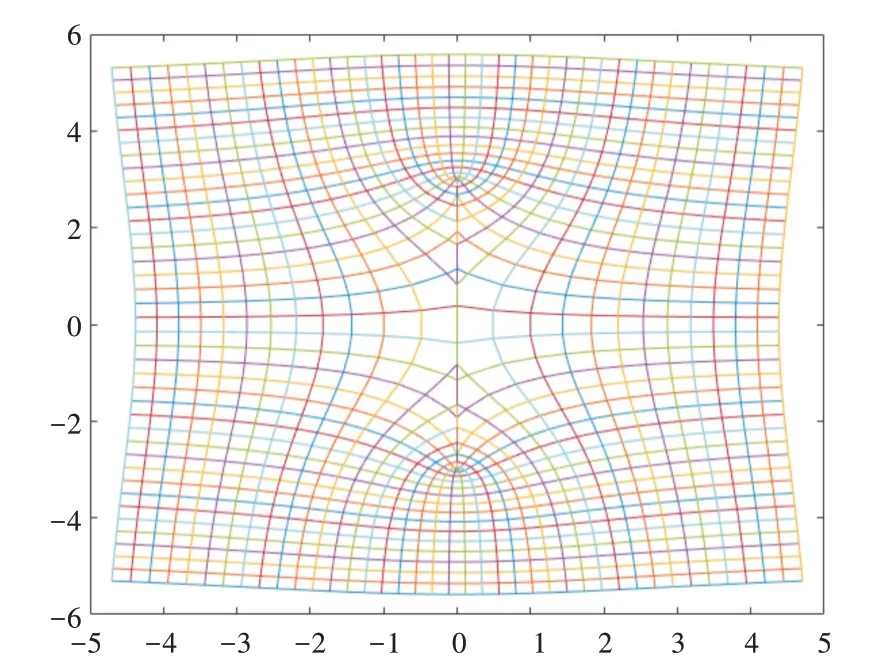
Fig.9 Fig.8 transformation results with the improved algorithm图9 图8 在改进算法下的变换结果

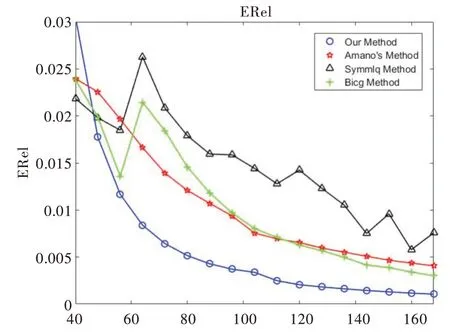
Fig.10 Erel（b）图10 Erel（b）

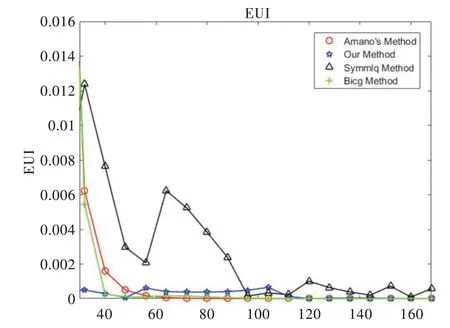
Fig.11 Vertical slit position error（b）图11 竖直狭缝位置误差

图13 是图12 通过数值保角变换后的图像，是一条竖直狭缝，在图中可以看到高楼的弯曲效果，从中可以更好地看出它们之间的角度关系。

Fig.12 Original image（b）图12 原始图像

Fig.13 Transform result of Fig.12图13 图12 的变换结果

4 结语

本文提出基于改进SSOR 法的数值保角变换计算法，解决了原有方法与一些传统方法在求解电荷量上的缺陷导致的数值保角变换结果误差大及不稳定等问题。从数值实验结果可知，本文方法在单连通外部区域例证中精度和稳定性较高，能够应用于图像领域。

但改进的SSOR 法在双连通及多连通上的数值效果仍有待检验，本文方法的一些因子常数选取是否为最佳值也需要继续研究和改善。

图像保角变换在医学图像处理中有着重要作用，未来可尝试处理医学图像中的一些实际问题，如将图像上狭小的缝隙在具有保角特性下放大观察，将一些具有干扰性的位置变为可忽视的狭缝。数值保角变换在流体力学中也有重要应用，可以用变换函数绘制无压缩流体在遇到障碍物时的曲线。