曾云辉，汪志红*，汪安宁，罗李平，俞元洪

（1.衡阳师范学院数学与统计学院，湖南衡阳421008；2.中国科学院数学与系统科学研究院，北京100190）

0 引 言

考虑具无界中立系数的三阶非线性微分方程

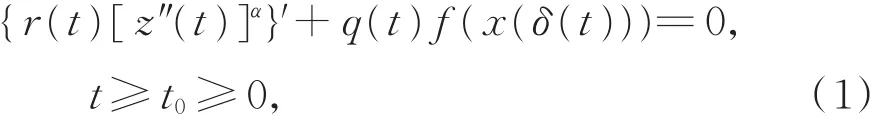
其中，z(t)=x(t)+p(t)x(τ(t))，f(x)∈C(R，R)，

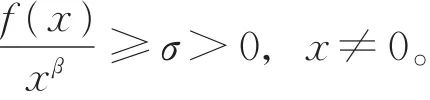
下文总假设下列条件成立：

(H1)α和β是 2个正奇数之比，

(H2)r(t) ∈C1(I，R+)，r"(t) ≥ 0，q(t) ∈C1(I，R+)，p(t)∈C(I，[1，∞ ))且p(t)不恒等于 1；

(H3) τ(t)，δ(t)∈C(I，(0，∞ ))，τ(t)≤t，δ(t)≤t，τ(t)在 I上 是 严 格 递 增 的 函 数 ，且

考虑以下2种情况：

和

式（1）的解指函数 x(t)∈ C1[Tx，∞ )，Tx≥t0使得r(t)[z″(t)]α∈C1[Tx，∞ )且在 [Tx，∞ )上满足 式（1） 。 本 文 仅 考 虑 式 （1） 中 满 足sup{|x(t)|：t≥T}＞0对一切T≥Tx成立的解。如果式（1）在[Tx，∞)上有任意大于零的点，则称其是振动的，否则，称其是非振动的。

中立型方程解的振动性和渐近性问题具有重要的理论和实践意义，例如，中立型微分方程可应用于核物理中原子核内部的电动势及高速计算机无损传输电路的网络设计等。对式（1）的振动性和渐近性研究越来越受关注［3-17］，以下为特例和更一般形式的方程：

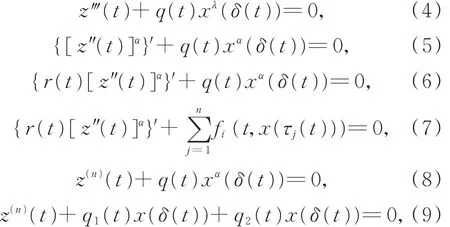
其中，λ，α＞ 0，n≥ 3，且n为正奇数。

近年来，文献［3-9，12，14-17］用不同方法研究了三阶中立型微分方程的振动性，得到了一些很好的结果，但其中大部分是式（1）的特例或与-1＜p0≤ p(t)≤ 0，0≤ p(t)≤ p0＜ 1 或 0≤ p(t)≤ p0＜∞的情况有关，而在p(t)＞1时关于三阶中立型微分方程的振动结果尚不多见。例如，文献［11-13］分别研究了式（8）、式（9）和式（6）的振动性，给出了一些振动结果，而这些结果是在条件τ◦δ=δ◦τ或τ◦δ=δ◦τ和 τ◦σ=σ◦τ下得到的，限制性较强，条件不易满足。最近，文献［14-15］取消了限制条件τ◦δ=δ◦τ，分别给出了式（4）和式（5）在正则条件下解的振动准则，但均未考虑非正则的情况，因此，研究式（1）在条件τ◦δ≠δ◦τ和非正则条件下的振动性问题是有意义的。

注 意 到 当 r(t)=1，α=β＞0，f(x(δ(t)))=xα(δ(t))时，式（1）变为式（5）。当 r(t)=1，α=1，β = λ，f(x(δ(t)))=xλ(δ(t))时，式（1）变为式（4）。因此，式（1）更具一般性，研究式（1）很有意义。

受文献［14］的启发，在条件τ◦δ≠δ◦τ和α≠β下，对式（1）展开研究，分别建立在正则条件

和非正则条件

下，式（1）的解x(t)或振动或渐近收敛于零的若干新的振动准则，所得结果推广、改进和统一了最近文献中若干熟知的结果。

如果没有特别说明，均假设下文中出现的函数不等式最终成立，即对一切充分大的t成立。

1 主要结果

为书写方便，引入记号：

其中，τ-1是 τ的反函数，m(t)和a(t)是本文设定的函数。

引理1 设(H1)～(H3)成立，x(t)是式（1）的正解，则当t≥t1，t1充分大时，z(t)具有下列3种性质：

(I)z(t)＞ 0，z"(t)＞ 0，z″(t)＞ 0，z‴(t)≤ 0，{r(t)[z″(t)]α}"≤ 0；

(II)z(t)＞ 0，z"(t)＜ 0，z″(t)＞ 0，z‴(t)≤ 0，{r(t)[z″(t)]α}"≤ 0；

(III)z(t)＞ 0，z"(t)＞ 0，z″(t)＜ 0，{r(t)[z″(t)]α}"≤ 0。

特别地，当式（10）成立时，z(t)满足性质（I）和（II）。

证明 引理1的证明类似于文献［17］中引理1的证明。此证略。

引理2 设(H1)～(H3)及p*(t)＞0成立，x(t)是方程（1）的正解，且z(t)满足性质（II）。若

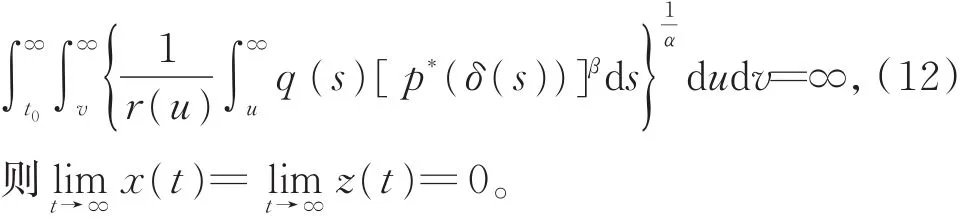
证明 设x(t)是方程（1）的最终正解，且z(t)满足性质（II），即存在 t1∈[t0，∞)，当 t∈[t1，∞)时，有 x(t)＞ 0，x(τ(t))＞ 0，x(δ(t))＞0。 由 z(t)的定义，有

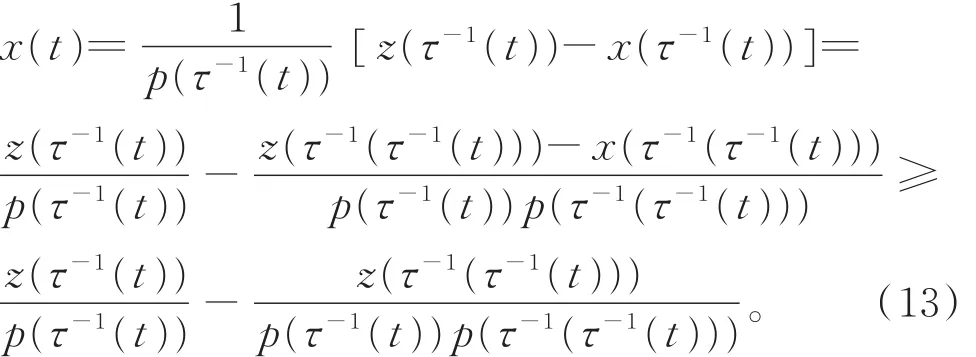
由于z(t)为减函数且τ(t)≤t，所以有

将式（14）代入式（13），有

从而有

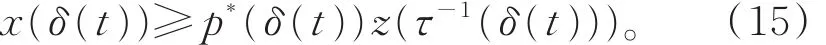
由式（1）和式（15），有

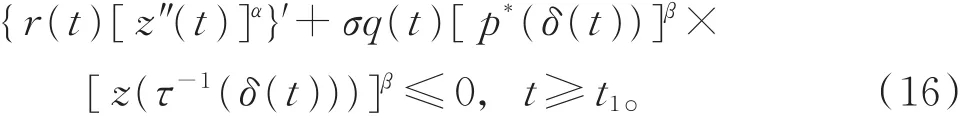
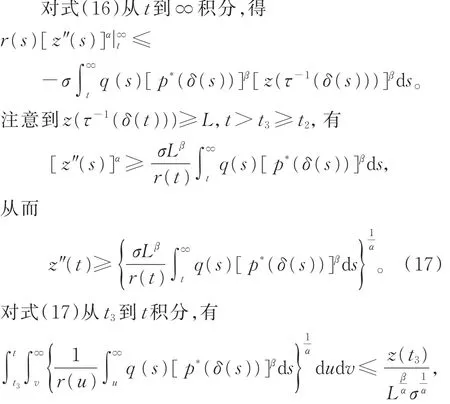
与 式（12）矛 盾 ，因 此 L=0。 又 由 于 0＜x(t)≤z(t)，因此

引理2得证。

引理3［2］设A＞ 0，B＞ 0，X ≥ 0，则

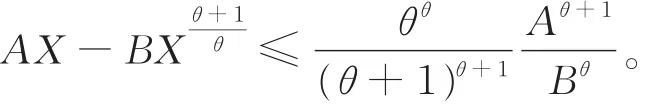
引理 4［1］设 f(t)∈ Cn([t0，∞ )，R+)，若 f(n)(t)对一切充分大的t最终定号，且存在t1≥t0，使得f(n-1)(t)f(n)(t)≤0对一切 t≥t1成立。如果则对任意 λ∈(0，1)，存在 tλ∈[t1，∞ )，使得在[tλ，∞ )上，有

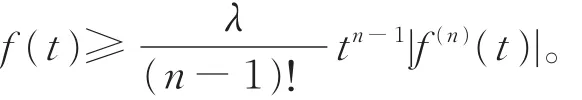
引 理 5［3］设 函 数 y(t)满 足 y(i)(t)＞ 0，i=0，1，…，k，且 y(k+1)(t)≤ 0，则有

引理6 设(H1)～(H3)和p*(t)＞0成立，x(t)是方程（1）的最终正解，且z(t)满足性质（I），若存在函数 m(t)∈ C1(I，R+)，满足

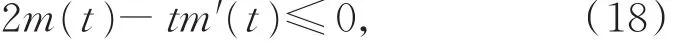
则z(t)满足

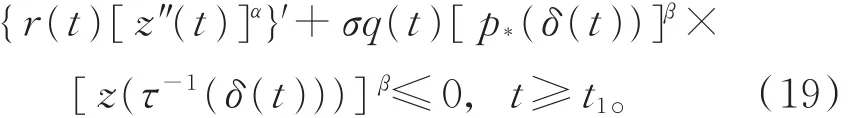
证明 设x(t)是方程（1）的最终正解，即存在充 分 大 的 t1，使 得 当 t≥ t1≥ t0时 ，有 x(t)＞ 0，x(τ(t))＞0，x(δ(t))＞0。 则式（18）和 τ-1(δ(t))＞t1成立（当x(t)最终为负时，可类似证明）。由引理2的证明，得到式（13）。又因为z(t)满足性质（I），由引理5可得

故

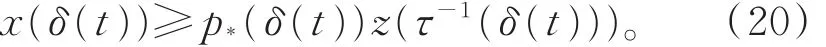
由式（1）和式（20），可得式（19）。

引理6得证。

引理6" 设(H1)～(H3)和Q(t)＞0成立，x(t)是式（1）的最终正解，且z(t)满足性质（III），若存在函数 a(t)∈ C1(I，R+)，满足

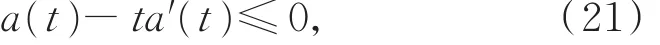
则z(t)满足

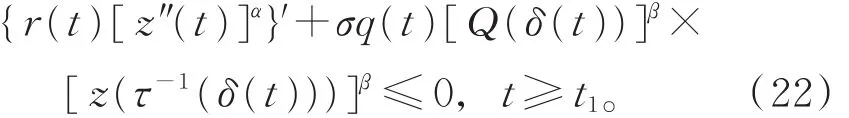
证明 与引理6的证明类似。此证略。

下面介绍本文的主要结果。

定理1 设(H1)～(H3)和式（12）成立。若式（10）和

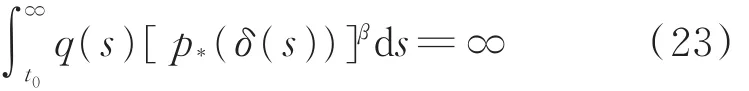
均成立，则式（1）的解x(t)都是振动的，或当t→∞时，x(t)→ 0。

证明 设式（1）存在非振动解x(t)。不失一般性，设 x(t)最终为正，由引理 1和式（10），z(t)只可能满足性质（I）和（II）。若z(t)满足性质（I），则由引理6，得式（19）成立，对式（19）从t1到t积分，有

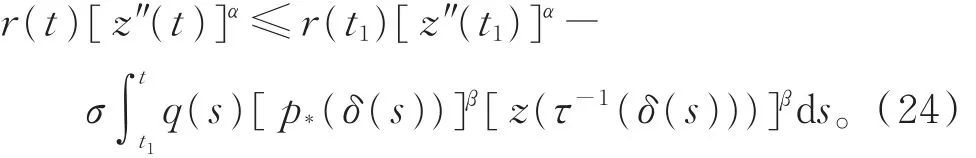
因 z(t)＞ 0，z"(t)＞ 0，故存在常数 M ＞ 0，使得当z(t)≥ M 时，有

进一步考虑，如果式（10）和式（23）其中之一不满足，将如何弥补？为此，首先考虑式（23）不成立的情况。

定理 2 设(H1)～(H3)、式（2）和式（12）成立。若式（10）成立且存在函数 m(t)∈C1(I，R+)，则满足式（18）。对于充分大的 t，有 p*(t)＞ 0和 p*(t)＞ 0。如果存在函数 η(t)∈C1(I，R+)、常数 λ∈(0，1)和L0＞ 0，满足

则式（1）的解x(t)都是振动的，或者当t→∞时，x(t)→ 0。

证明 设式（1）存在非振动解x(t)。不失一般性，设 x(t)最终为正，即存在t1∈[t0，∞ )，当 t≥ t1时，使得 x(t)＞ 0，x(τ(t))＞ 0，x(δ(t))＞ 0， p*(t)＞ 0，p*(t)＞0，τ-1(δ(t))＞t0及式（18）成立（当 x(t)最终为负时，可类似证明）。因式（10）成立，故z(t)只可能满足性质(I)和(II)。首先，设z(t)满足性质(I)，由引理 5，可得

m(t)∈C1(I，R+)满足式（18）。对于充分大的 t，满足 p*(t)＞0 和 p*(t)＞0，如 果 存 在 函 数η(t)∈C1(I，R+)、常 数 λ∈(0，1)、L0＞ 0 和 m0＞ 0，满足

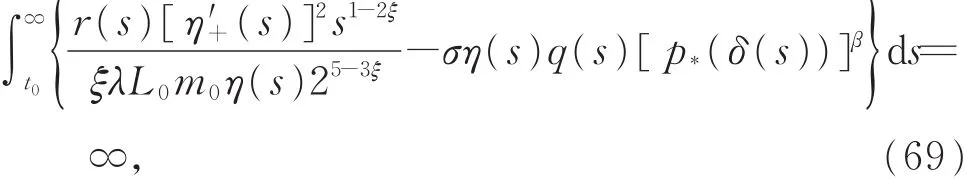
则式（1）的解x(t)都是振动的，或当t→∞时，x(t)→ 0。

证明 设x(t)是方程（1）的非振动解。不失一般性，设 x(t)最终为正，故存在 t1∈[t0，∞ )，当 t＞ t1时，使得 x(t)＞0，x(τ(t))＞0，x(δ(t))＞ 0，p*(t)＞0，p*(t)＞ 0，τ-1(δ(t))＞ t0及 式（18）成 立 。 因 式（10）成立，故 z(t)只可能满足性质 (I)和(II)。首先，设 z(t)满足性质(I)，注意到式（3）和(H3)，类似于定理6的证明，可得式（67）。

同定理2，定义函数w(t)，由式（19）、式（27）～式（29）和式（67），可得

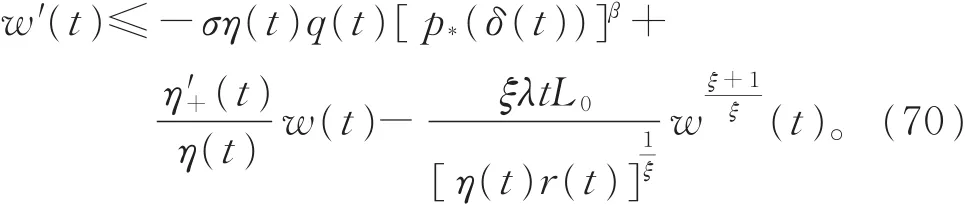
后续证明与定理3的证明类似，此证略。

3 例 子

例1 考虑具有无界中立系数的三阶非线性微分方程

故式（25）成立。因此，由定理2知，式（71）的解x(t)都是振动的或者渐近收敛于零。由于α≠β，因此文献［3-16］及其引文中的振动结果均不适用于式（71）。