张伟，周静

（河南财经政法大学数学与信息科学学院，河南郑州450046）

20世纪40年代，GABOR[1]将分解复杂信号为简单信号的思想引入信号处理，借助此奠基性方法，DUFFIN等[2]于1952年提出Hilbert空间标架概念，当时并未引起重视。1986年，DAUBECHIES等[3]再次引入标架概念并对其进行了发展，通常标架才引起关注。在随后的30多年中，标架理论发挥了重要作用［4］，并在众多领域得到应用［5-6］，例如用标架进行编码、通信以及测度量化等。

标架是向量生成集，有类似于标准正交基的重构公式，但系数不唯一。设H是可分的Hilbert空间，对于向量列 {fi}i∈I⊂H，如果存在正常数A，B，对f∈H，有

则称{fi}i∈I为H空间中的标架，A和B分别为标架的下界和上界。

1993年，ALI等[7]将标架的概念推广至带有Radon测度的局部紧空间，引入连续标架的概念。2006年，SUN[8]又将标架由向量序列推广至算子列，提出广义标架的概念。2008年，ABDOLLAHPOUR等[9]将积分应用于广义标架，引入连续广义标架的概念。构造新标架是标架应用的中心问题之一，OBEIDAT等［10］研究了 Hilbert空间中标架的和，用已有标架构造了大量新标架，并给出了Hilbert空间中 的 Bessel序列 {fn}和 {gn}以及算 子L1，L2，使得{L1fn+L2gn}构成新标架的充要条件，但是该文仅考虑了2个标架和的情形。那么，类比于标架（或Bessel序列），连续广义标架是否也有类似结果？基于此，笔者考虑连续广义标架的和，借助算子工具，利用已有连续广义标架构造新的连续广义标架；并给出有限个连续广义标架和构成新的连续广义标架的充要条件。

1 预备知识

文中涉及的相关符号、概念及基本性质详见文献［5-6，9］。其中，U，V为复Hilbert空间，J为可数的指标集，(Ω，μ)为所含测度μ是正的测度空间，{Vω}ω∈Ω为 V 的闭子空间列，L(U，Vω)为所有 U 到Vω的线性有界算子的集合，若 Vω=U，记L(U，Vω)=L(U)，IU为U上的恒等算子。

定义1[7]设U为复Hilbert空间，(Ω，μ)为含有正测度μ的测度空间，如果满足：

（i）F 是 弱 可 测 的 ，即 对 所 有 的 f∈U，ω→ f，F(ω)是Ω上的可测函数；

（ii）存在正常数A和B，对任意f∈U，均有

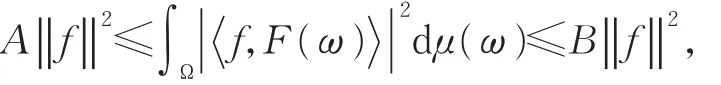
其中，A和B分别为连续标架的下界和上界，则称映射F：Ω→U为关于(Ω μ)的连续标架。

定义 2[8]给定算子 {Λj∈L(U，Vj)}j∈J，如果存在常数0＜A≤B＜∞，使得对任意f∈U，有

则称 {Λj}j∈J为 U 关于 {Vj}j∈J的广义标架，其中，A和B分别为广义标架的下界和上界。

定义3[9]如果满足：

（i）对固定的f∈U，ω→Vωf是强可测的；

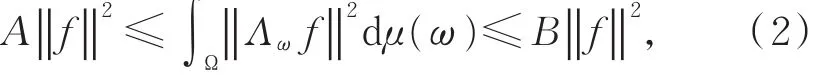
其中，A和B分别为此标架的下界和上界，则称算子序列{Λω∈L(U，Vω)}ω∈Ω为U关于{Vω}ω∈Ω的连续广义标架；如果式（2）仅右半不等式成立，则称{Λω}ω∈Ω为 U关于{Vω}ω∈Ω的连续广义 Bessel序列；如果 A=B(=1)，则称 {Λω}ω∈Ω为 U 关于 {Vω}ω∈Ω的紧（Parseval）连续广义标架。

定义空间

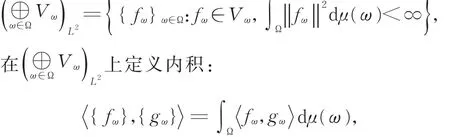
对于连续广义 Bessel序列 {Λω}ω∈Ω，称线性有界算子

为{Λω}ω∈Ω的连续广义合成算子，称共轭算子

为{Λω}ω∈Ω的连续广义分析算子，称线性算子

为连续广义标架算子。其中，S为线性有界、自伴、正的可逆算子。

引理1[3]设T：U→K为有界满射算子，存在有界算子T†：K→U，使得TT†：K→K，TT†f=f，则称T†为T的伪逆。

2 主要结果及证明

在一定条件下，利用已有连续广义标架构造新连续广义标架，特别地，给出有限个连续广义标架和构成新的连续广义标架的充要条件。

定理 1 设 {Λω}ω∈Ω为 U 关于 {Vω}ω∈Ω的连续广义标架且标架算子为S，标架界分别为A和B。若 P ∈L(U)，则 {ΛωP}ω∈Ω是 U 关于 {Vω}ω∈Ω的连续广义标架当且仅当存在正常数α使得对任意在此情况下，连续广义标架 {ΛωP}ω∈Ω的标架算子为 P*SP，标架界分别为

证明 假设 {ΛωP}ω∈Ω是 U 关于 {Vω}ω∈Ω的连续广义标架，且标架界分别为C和D。对任意f∈U，有

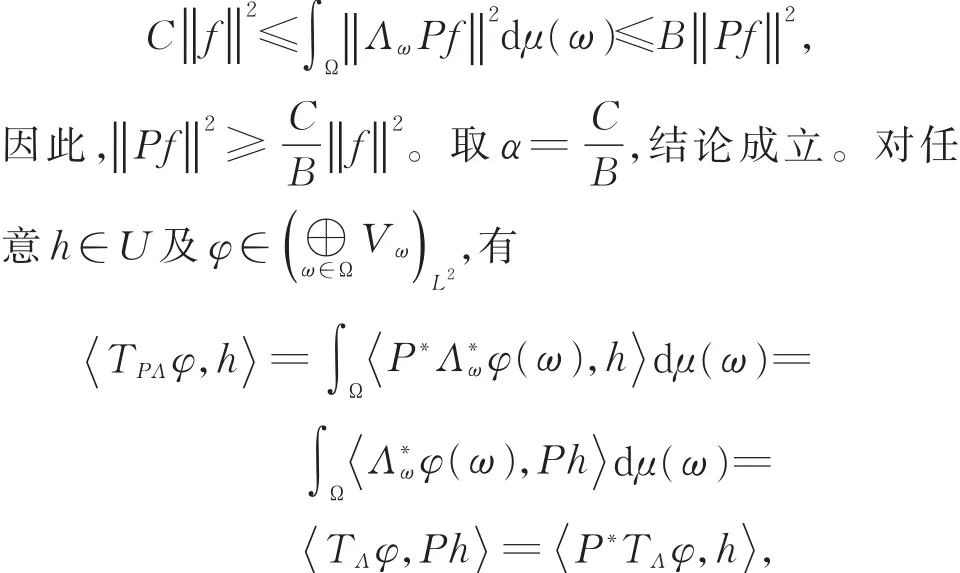
故TPΛ=P*TΛ，易知=P，经简单计算，可知{ΛωP}ω∈Ω的标架算子为P*SP。

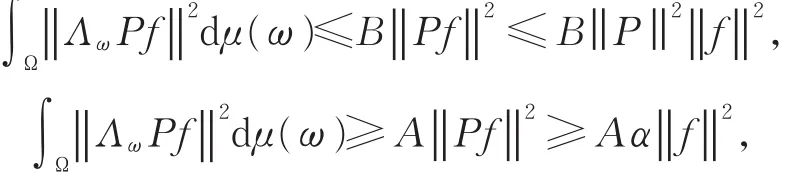
所以，{ΛωP}ω∈Ω是U关于{Vω}ω∈Ω的连续广义标架且标架下界和上界分别为Aα和B‖P ‖2。

证毕。

由定理1，可直接推得

推论 1 设 {Λω}ω∈Ω是 U 关于 {Vω}ω∈Ω的紧连续广义标架，标架界为 A。若 P∈L(U)，则{ΛωP}ω∈Ω是 U 关于 {Vω}ω∈Ω的紧连续广义标架且标架界为 α当且仅当对任意f∈U，有

推论 2 设 {Λω}ω∈Ω是 U 关于 {Vω}ω∈Ω的连续广义标架且标架算子为S，标架界分别为A和B。若 P ∈L(U)，则 {ΛωP}ω∈Ω是 U 关于 {Vω}ω∈Ω的连续广义标架当且仅当P是有界满射算子。在此情况下，连续广义标架{ΛωP}ω∈Ω的标架算子为 P*SP，标架界分别为

证明 若P是有界满射算子，由引理1，存在伪逆 算 子 P†使 得 PP†=IU，故 对 任 意 f∈U，有，由定理1知，结论成立。

证毕。

推论 3 设 {Λω}ω∈Ω是 U 关于 {Vω}ω∈Ω的连续广义标架且标架算子为S，标架界分别为A和B。若 P ∈ L(U)，则 {Λω+ ΛωP}ω∈Ω是 U 关于 {Vω}ω∈Ω的连续广义标架当且仅当IU+P是有界满射算子。在此情况下，连续广义标架{Λω+ΛωP}ω∈Ω的标架算子为(IU+P)*S(P+IU)，标架界分别为特别地，若P是正算 子（或 仅 对 某 些 ε＞0，IU+P＞ε），则 {Λω+ΛωP}ω∈Ω是U关于{Vω}ω∈Ω的连续广义标架且标架算子为S+P*S+SP+P*SP。

定 理 2 设 {Λω}ω∈Ω和 {Γω}ω∈Ω为 U 关 于{Vω}ω∈Ω的2个连续广义标架且合成算子分别为TΛ和TΓ。设L1，L2∈L(U)，若TΛT*Γ=0且L1或L2是满射算子，则 {ΛωL1+ ΓωL2}ω∈Ω是 U 关于 {Vω}ω∈Ω的连续广义标架。

证 明 因 为 {Λω}ω∈Ω和 {Γω}ω∈Ω为 U 关 于{Vω}ω∈Ω的2个连续广义标架，所以存在常数0＜A2≤B2＜∞ 和 0＜A3≤B3＜∞，使得对任意f∈U，有

又因为TΛT*Γ=0，所以对任意f∈U，有

因此，对任意f∈U，有

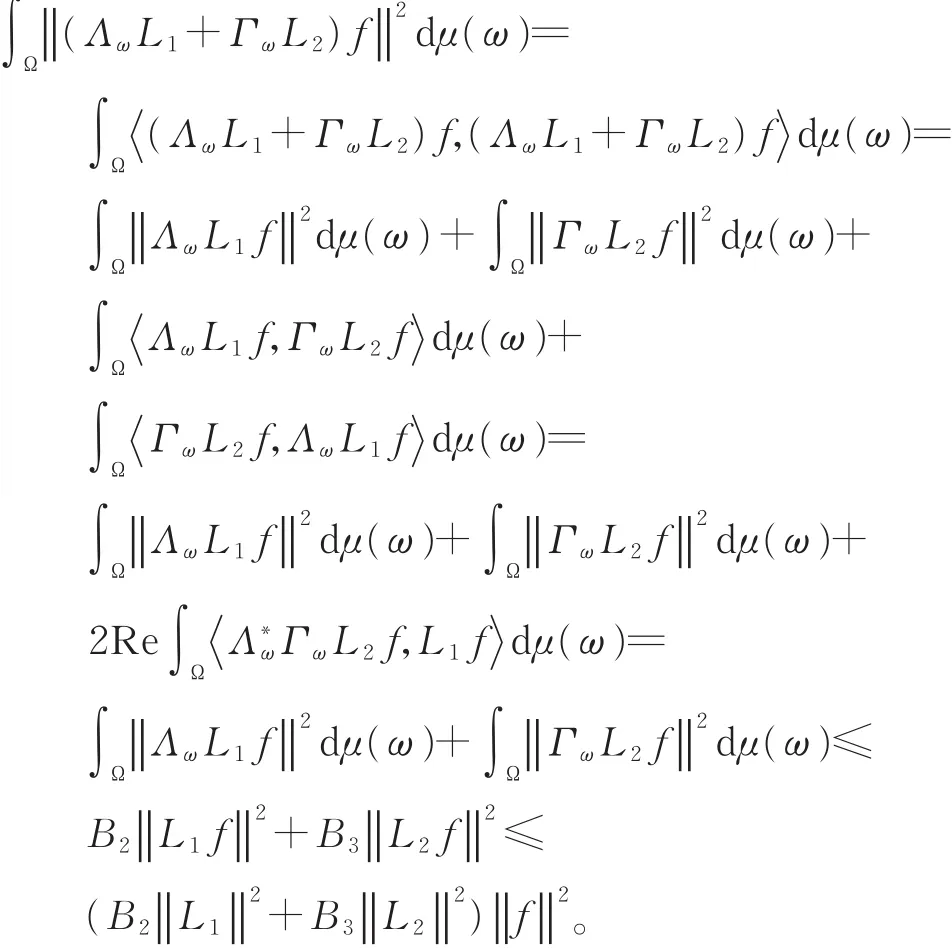
不失一般性，假设L1是满射算子，由推论2的证明过程知，存在常数C使得对任意f∈U，有

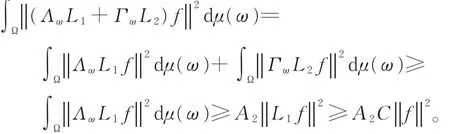
所以，{ΛωL1+ ΓωL2}ω∈Ω是 U 关于 {Vω}ω∈Ω的连续广义标架。

证毕。

在定理2中，取L1=0，L2为满射算子，可得

推 论 4 设 {Λω}ω∈Ω和 {Γω}ω∈Ω为 U 关 于{Vω}ω∈Ω的2个连续广义标架且合成算子分别为TΛ和TΓ。设L2∈L(U)，若TΛT*Γ=0且L2为满射算子，则{Λω+ ΓωL2}ω∈Ω是 U关于 {Vω}ω∈Ω的连续广义标架。对任意自然数 a，{Λω+ ΓωLa2}ω∈Ω也是 U关于{Vω}ω∈Ω的连续广义标架。

由定理2，可直接推得

推 论 5 若 {Λω}ω∈Ω和 {Γω}ω∈Ω为 U 关 于{Vω}ω∈Ω的2个紧连续广义标架且TΛT*Γ=0，则{Λω+Γω}ω∈Ω是 U 关于 {Vω}ω∈Ω的标架界为 2 的Parseval连续广义标架。

定理 3 设 {Λω}ω∈Ω是 U 关于 {Vω}ω∈Ω的连续广义标架，且标架界分别为A和B，{Γω}ω∈Ω是U关于 {Vω}ω∈Ω的连续广义 Bessel序列，且合成算子为TΓ，对于 2个给定的正序列 {aω}ω∈Ω和 {bω}ω∈Ω，如果则 {aΛ+bΓ}是 U 关 于ωωωωω∈Ω{Vω}ω∈Ω的连续广义标架。

证明 一方面，对任意f∈U，有

证毕。

在定理3中，取aω=bω=1，可得以下推论。

推论 6 设 {Λω}ω∈Ω是 U 关于 {Vω}ω∈Ω的连续广义标架，且标架界分别为A和B。{Γω}ω∈Ω为U关于 {Vω}ω∈Ω的连续广义 Bessel序列，且合成算子为则 {Λω+Γω}ω∈Ω是 U 关 于{Vω}ω∈Ω的连续广义标架。

推论 7 设 {Λω}ω∈Ω为 U 关于 {Vω}ω∈Ω的连续广义标架，且标架界分别为A和B，标架算子为SΛ，{Γω}ω∈Ω为 U关于{Vω}ω∈Ω的连续广义Bessel序列，且Bessel界为M。对任意常数a和b，如果|b|2＜1，则 {aΛω+bΓω}ω∈Ω是 U 关 于{Vω}ω∈Ω的连续广义标架。

最后，给出有限个连续广义标架和构成新连续广义标架的充要条件。

定 理 4 设 {Λ1，ω}ω∈Ω，{Λ2，ω}ω∈Ω，···，{Λk，ω}ω∈Ω均为 U关于{Vω}ω∈Ω的连续广义标架，{ai}(i=1，2，···，k)为任意标量，则是U的连续广义标架当且仅当存在β＞0及p∈{1，2，…，k}使得对任意f∈U，有

由此可得

充分性。设对于每个 p∈ {1，2，···，k}，Ap和 Bp分别为连续广义标架 {Λp，ω}ω∈Ω的下界和上界，一方面，常数β＞0对任意f∈U，满足