张玉环 任勇生 张金峰

(山东科技大学机械电子工程学院，山东青岛266590)

在机械工程领域，蒸汽机、燃气机、内燃机驱/传动轴、机床主轴以及镗/铣削刀具，均可简化为一类典型的旋转轴力学模型，精确地描述旋转轴的动力学建模和动力学特性对于提高机械效率和/或者机床加工精度具有重要的理论指导意义。旋转轴的动力学建模理论包括经典的Euler-Bernoulli梁理论、在Euler-Bernoulli梁模型中引入转动惯量的Rayleigh梁理论，以及在Rayleigh梁模型中引入剪切变形的Timoshenko梁理论。其中，Euler-Bernoulli梁理论适用于分析细长轴的低阶振动特性。既然镗/铣削系统的颤振大多数是围绕细长刀杆结构的低阶固有频率发生的[1]，并且由于旋转轴上陀螺效应的存在，转动惯量的影响也是不容忽视的，所以，为了精确揭示旋转细长轴的动力学特性，采用Rayleigh梁理论对旋转轴进行结构动力学建模与数值分析是十分必要的。

Dimentberg[2]采用Euler-Bernoulli梁导出旋转轴的特征方程。Lee等[3]给出旋转Rayleigh简支轴和悬臂轴的特征值和特征函数。Katz等[4]基于Timoshenko梁理论分析了旋转轴的动力学特性。Zu等[5-6]基于模态分析法对具有不同边界条件的旋转Timoshenko轴进行自由振动分析。Shiau等[7]给出旋转简支Rayleigh轴涡动频率的封闭解。Sheu等[8]建立简支旋转Rayleigh轴的涡动频率的解析表达式。Banerjee等[9]导出Euler-Bernoulli复合材料梁的动刚度矩阵并采用Wittrick-Williams算法求解自由振动和临界转速。任勇生等[10]建立Euler-Bernoulli黏弹性复合材料旋转轴的运动方程，采用Galerkin法求解得到涡动频率与阻尼。

经典的求解方法是利用分离变量法对偏微分运动方程进行求解，建立表征模态振型的特征方程，由于特征方程与特征值是涡动频率和转速的非线性函数，所以无法得到涡动频率解的封闭表达式，只能采用数值计算的方法求解非线性特征方程，以获得Rayleigh轴的涡动频率和临界转速。Galerkin法是一种寻求振动系统连续偏微分方程近似解的实用、有效近似解法，已经在线性与连续非线性振动系统的求解中得到了广泛的应用[11-12]。

本文研究旋转悬臂轴的涡动频率和临界转速。为了获得涡动频率和临界转速的近似解，首先给出基于分离变量解法的旋转悬臂轴的涡动频率和临界转速求解数学公式，其次采用Galerkin法将轴的偏微分运动方程化为常微分方程，然后通过求解矩阵特征值问题得到涡动频率和临界转速的近似解，分别选用不旋转Euler-Bernoulli轴的振型函数和旋转Rayleigh轴的振型函数为Galerkin过程的试探函数。并且将Galerkin法与基于经典方法的计算结果进行对比分析。

1 数学模型

1.1 运动方程与自由振动经典解

单位长度质量为m，转速为Ω，长度为L，半径为R的圆截面均匀无阻尼旋转轴(如图1所示)的运动方程为[8]

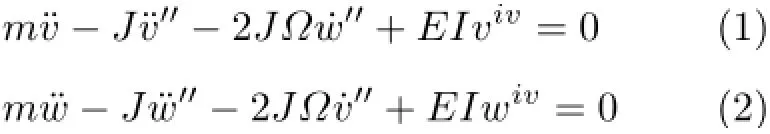
式中，v和w分别表示轴上任意一点x沿y和z方向的位移，E表示杨氏模量，I表示直径惯性矩，J表示轴的转动惯量。

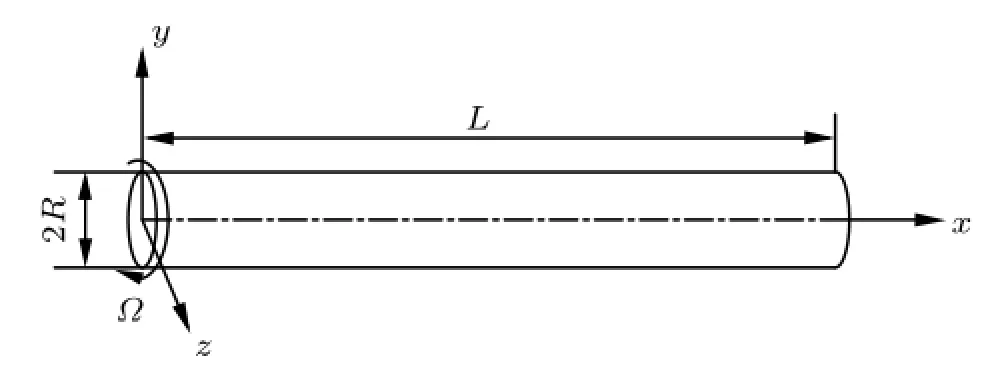
图1 旋转轴结构简图

m和J计算表达式分别为

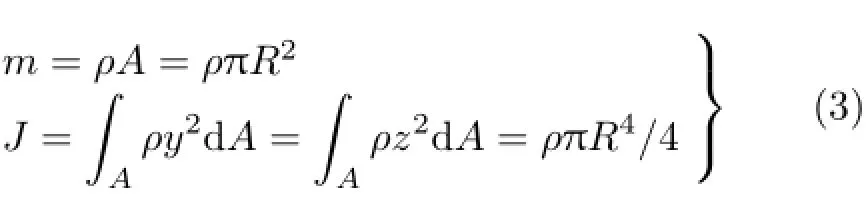
式中，ρ为密度。

对运动方程采用无量纲变换

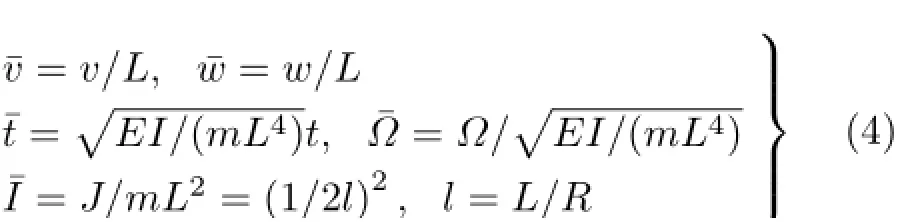
式中，EI表示抗弯刚度。

无量纲运动方程为

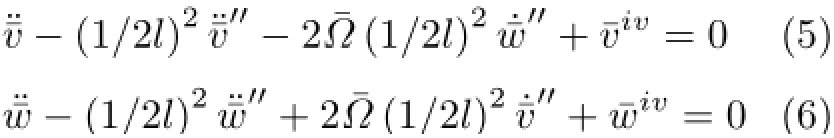
引入复变量U=¯v+i¯w，运动方程(5)和方程(6)可以合并为一个复方程

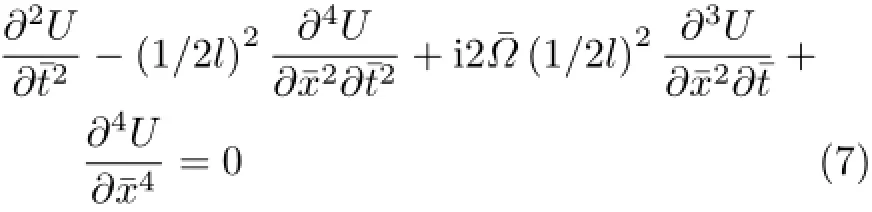
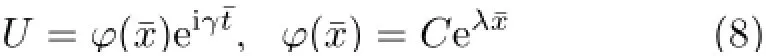
将式(8)代入式(7)，得

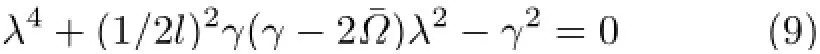
方程(9)的解为

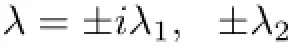
其中

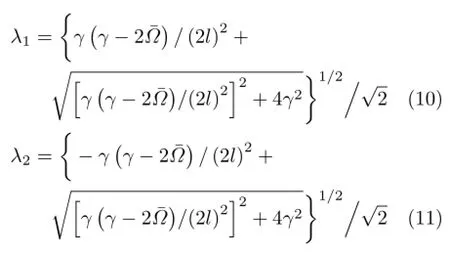
涡动振型函数为

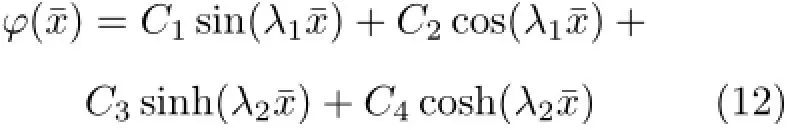
其中，系数C1，C2，C3，C4由边界条件确定。

悬臂轴在¯x=0固支，在¯x=L自由，则边界条件可以表示为

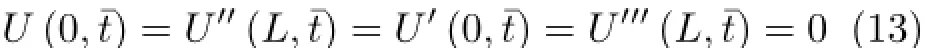
由条件(13)得到特征方程

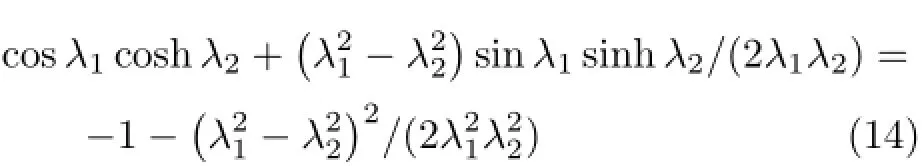
对应的涡动振型函数为

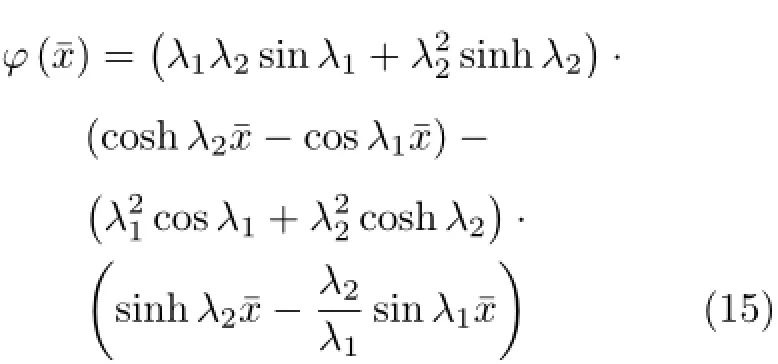
为了求得涡动频率，首先将式(10)和式(11)代入方程(14)，得到的方程(14)是涡动频率的超越方程，没有封闭解。借助于数值解法，可以获得它的两个根，其中，正根对应于正进动涡动频率γf，负根对应于反进动涡动频率γb。如果将求解得到的涡动频率代入方程(15)，即可得到对应的正、反进动涡动振型函数φf和φb。为简单起见，φ(¯x)，λ1和λ2的下标j不再写出。

1.2 Galerkin近似解

1.2.1 采用旋转Rayleigh梁振型函数

假设

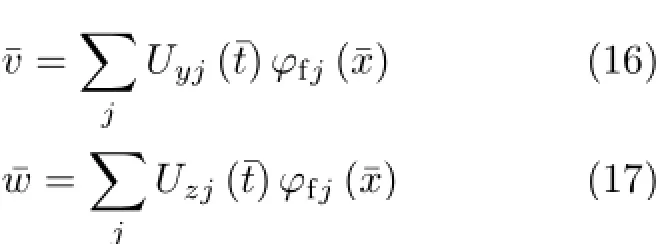
将式(16)和式(17)代入式(5)和式(6)，再乘以φj，在[0，1]上积分，得

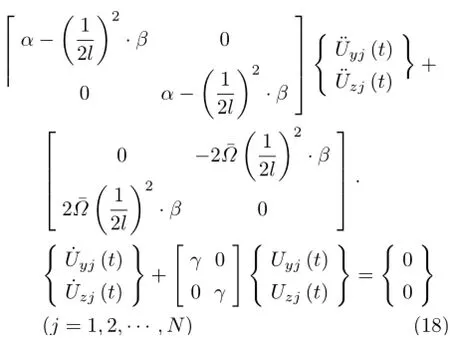
其中

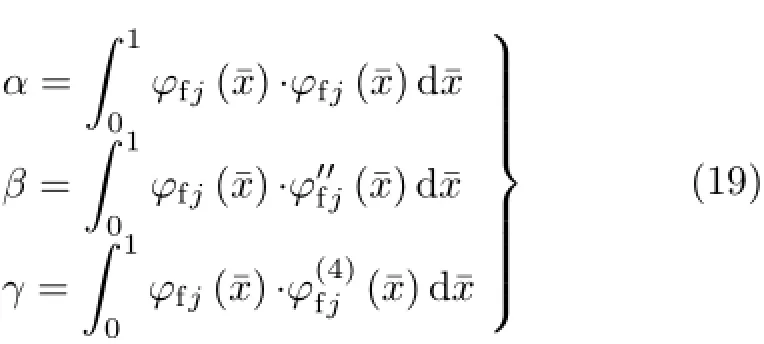
通过求解振动方程组的特征值问题，可以得到涡动频率。

1.2.2 采用不旋转Euler-Bernoulli梁振型函数

令

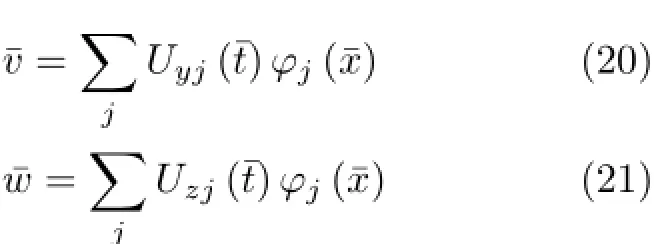
其中，不旋转Euler-Bernoulli梁的振型函数φj(¯x)为

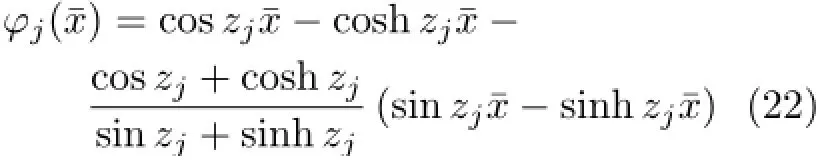
特征方程为

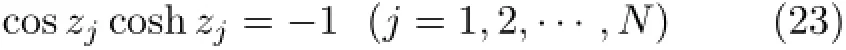
将式(20)和式(21)代入式(5)和式(6)可得相同形式的方程组(18)，方程系数为

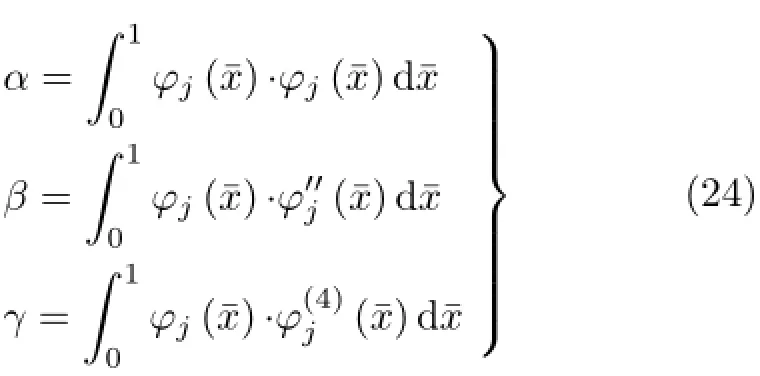
与不旋转Euler-Bernoulli梁的振型函数(22)相比，旋转Rayleigh梁的振型函数(15)不仅包含了无量纲旋转速度¯Ω，同时也包含了无量纲转动惯量l的影响。如果在方程(10)和方程(11)中令旋转速度和转动惯量同时为零，则有λ1=λ2。由此得到的特征方程(14)和涡动振型函数(15)即可分别退化为不旋转Euler-Bernoulli梁的特征方程(23)和振型函数(22)。

2 数值结果与讨论

图2 和图3给出利用式(15)画出的旋转轴的归一化正进动和反进动振型曲线，并且为了比较，图中还展示了利用式(22)画出的不旋转Euler-Bernoulli梁的振型曲线。图2表示旋转速度对正、反进动振型曲线的影响，结果表明，正、反进动振型之间是存在差别的，这种差别随着转速的增加而增加；另外，旋转振型曲线与不旋转振型曲线之间的差别也随着转速的增加而增加。图3表示长径比对正、反进动振型曲线的影响，结果表明，正、反进动振型曲线之间的差别随着长径比的增加而减小；另外，旋转振型曲线与不旋转振型曲线之间的差别随着长径比的增加而减小，由此可见，长径比对振型曲线的影响与转速对振型曲线的影响刚好是相反的。

图4～图6 表示前三阶涡动频率随长径比的变化曲线(Ω=50)，其中包括采用式(10)，式(11)和式(14)得到经典解，以及分别采用旋转振型和不旋转振型的Galerkin近似解。结果表明，采用上述三种解法得到的结果基本一致。

图7～图9 表示前三阶正进动涡动频率随转速变化曲线(l=40)。直线Ω=ω与+ωj(j=1，2，3)交点的横坐标Ωcj代表第j阶临界转速。结果表明，正进动涡动频率随转速变化曲线的经典解与基于旋转振型的Galerkin解重合，基于不旋转振型的Galerkin解虽然与上述两种解法得到的曲线不重合，但是相互之间的差距非常小。

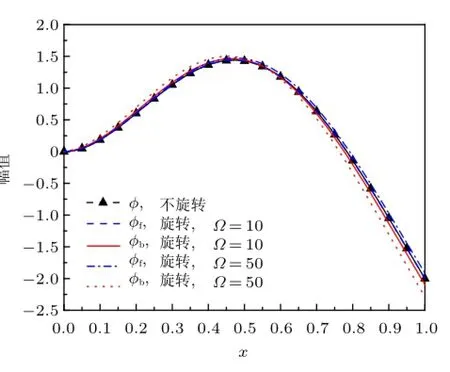
图2 旋转轴的正进动和反进动振型(l=15)

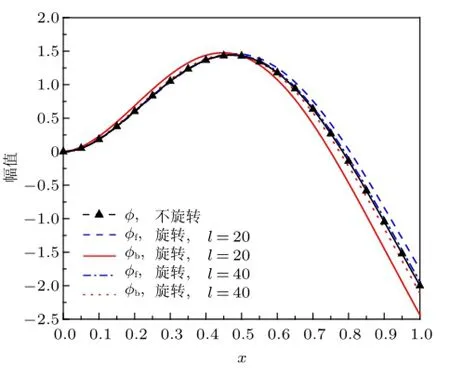
图3 旋转轴的正进动和反进动振型(Ω=50)

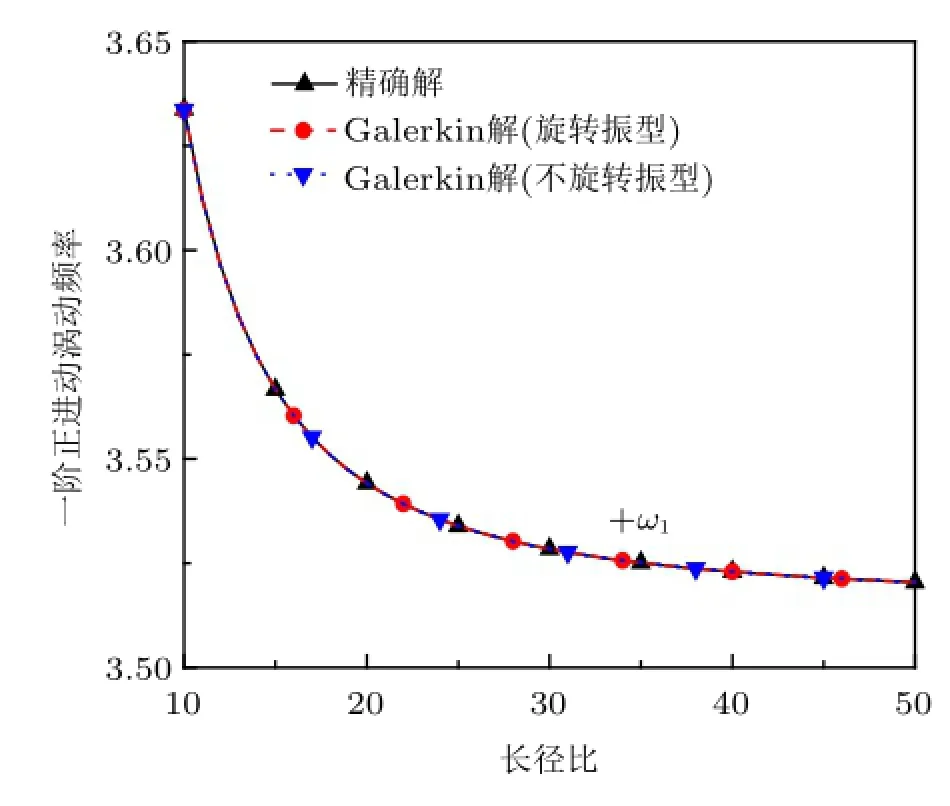
图4 第一阶涡动频率随长径比变化曲线(Ω=50)

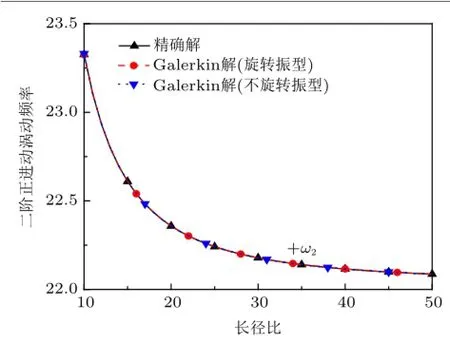
图5 第二阶涡动频率随长径比变化曲线(Ω=50)

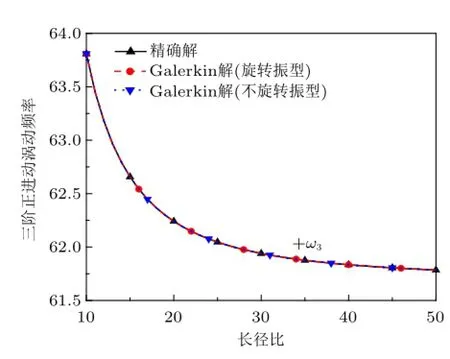
图6 第三阶涡动频率随长径比变化曲线(Ω=50)

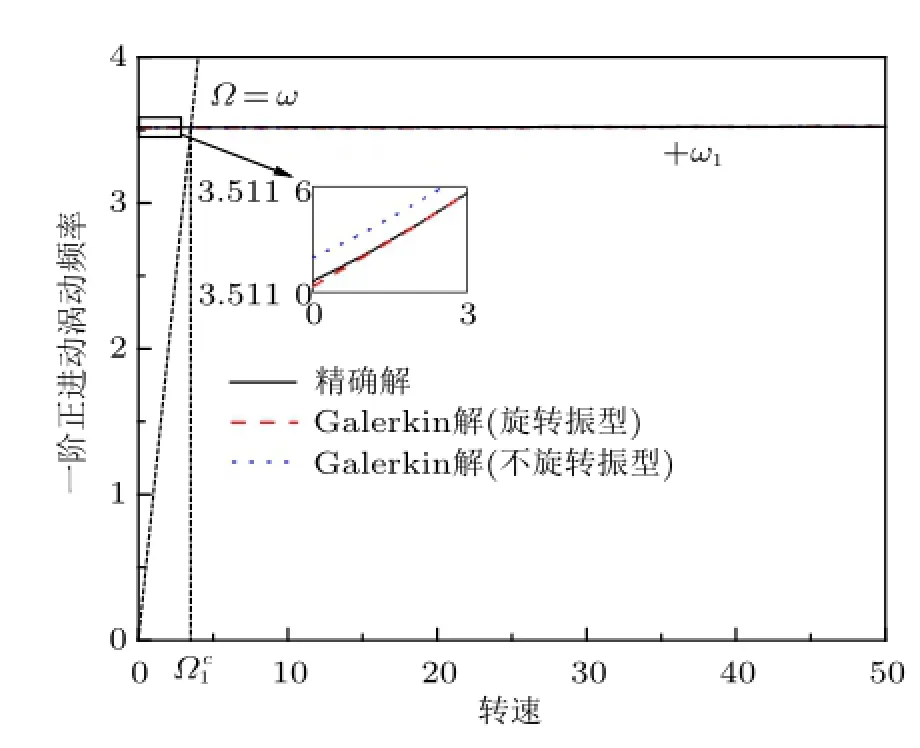
图7 第一阶正进动涡动频率随转速变化曲线(l=40)

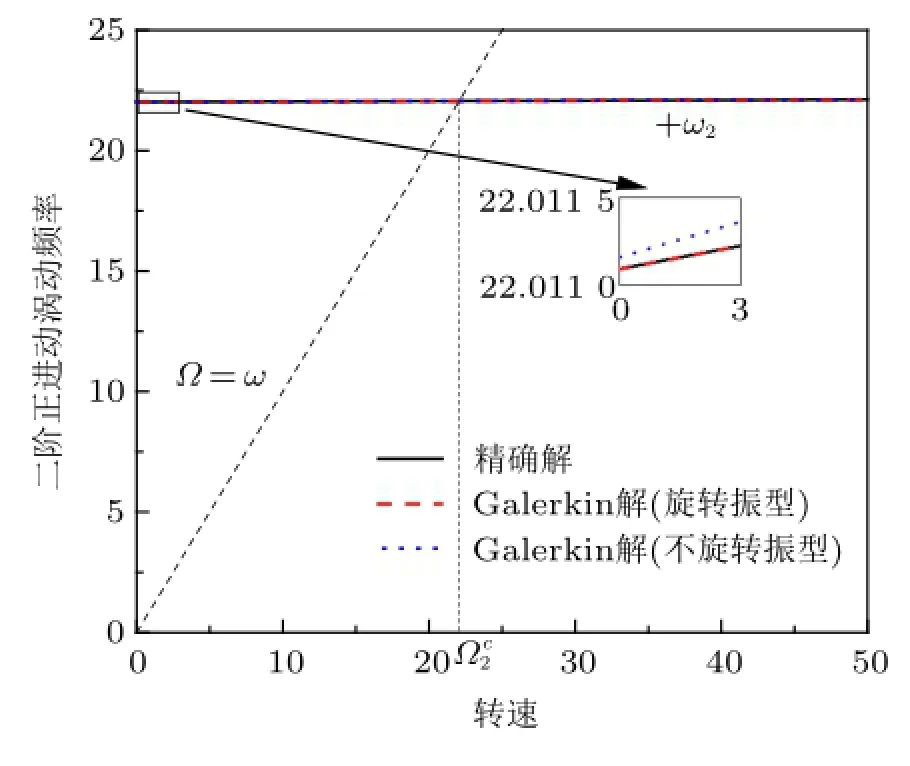
图8 第二阶正进动涡动频率随转速变化曲线(l=40)

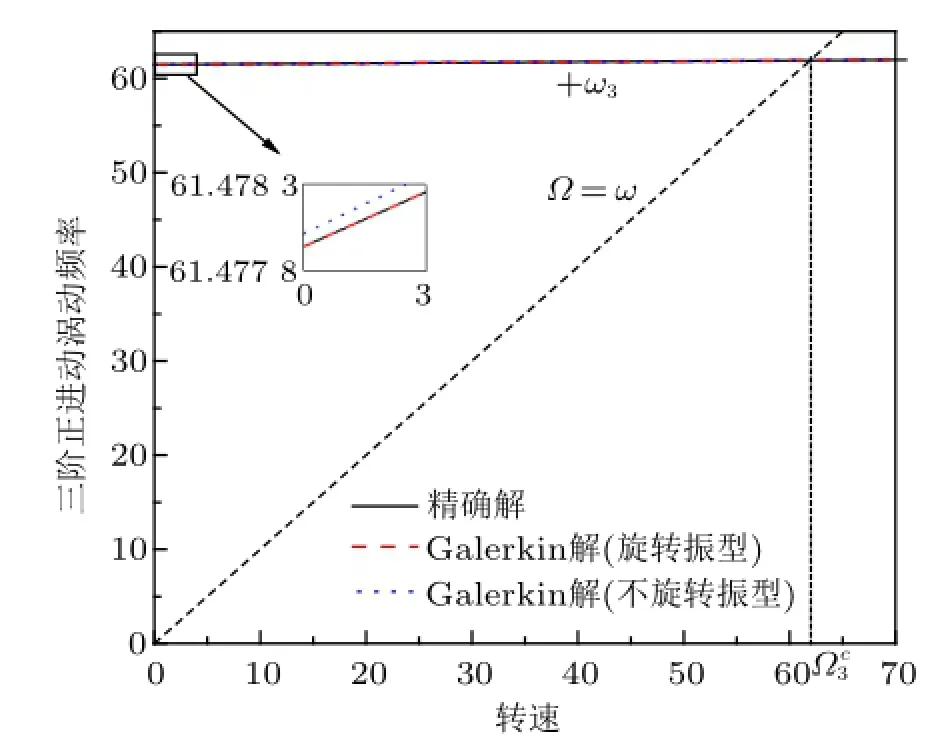
图9 第三阶正进动涡动频率随转速变化曲线(l=40)

表1 表示长径比对前三阶临界转速的影响。其中列出了采用三种不同方法得到的计算结果。方法1、方法2和方法3分别表示经典解法、基于旋转和不旋转振型的Galerkin法。结果表明，临界转速随着长径比的增加而减小。采用三种方法得到的临界转速的数值是相同的。

为了检验Galerkin近似解法的收敛性，表2给出振型函数个数N对前三阶涡动频率的影响。其中，下标n表示不旋转，r表示旋转，“+”表示正进动；“-”表示反进动。结果表明，采用Galerkin法得到的近似解具有很好的收敛性，例如，采用不旋转振型函数求解，N=3即可得到收敛的第一阶正进动频率+ωn1=3.544 5，反进动频率-ωn1=3.519 3。如果采用旋转振型函数，则取得相同收敛结果所需要的振型函数的个数是N=4。采用经典解法得到的前三阶涡动频率为：+ω1=3.544 2，-ω1=3.514 9，+ω2=22.358 2，-ω2=21.990 9，+ω3=62.241 1，-ω3=61.405 9。这说明本文的Galerkin近似解收敛到经典解。因此，为了确保收敛性，在本文的数值结果中，不旋转振型函数的个数为3，旋转振型函数的个数为4。表3表示前三阶临界转速近似解的收敛性。结果表明，振型函数只要取较少的项数即可得到足够精确的结果(注：采用经典解法得到的前三阶临界转速分别为3.518 7，22.026 5，62.601 5)。

表1 长径比对前三阶临界转速的影响

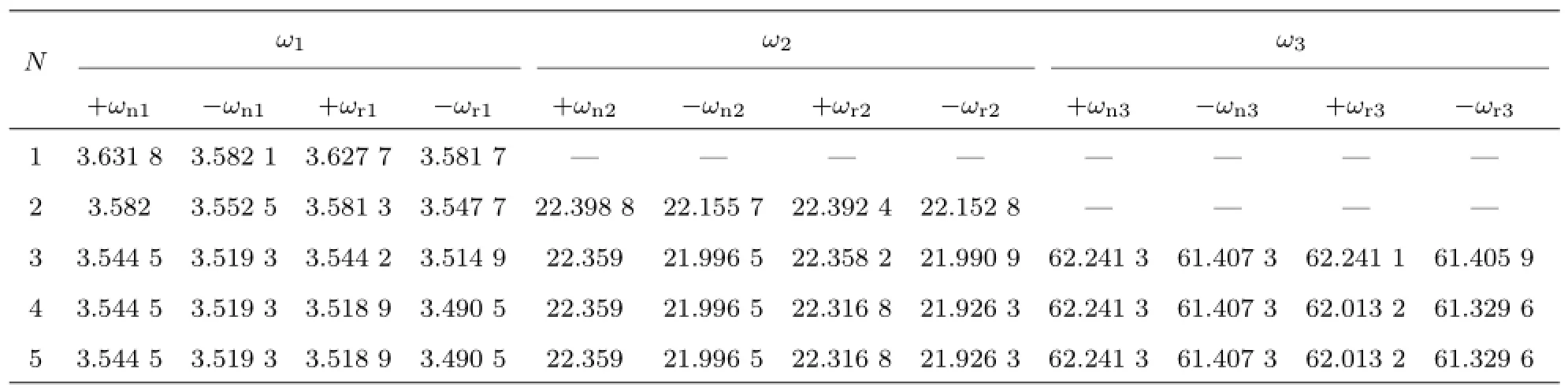
表2 前三阶涡动频率随振型函数个数的变化(l=20，Ω=50)

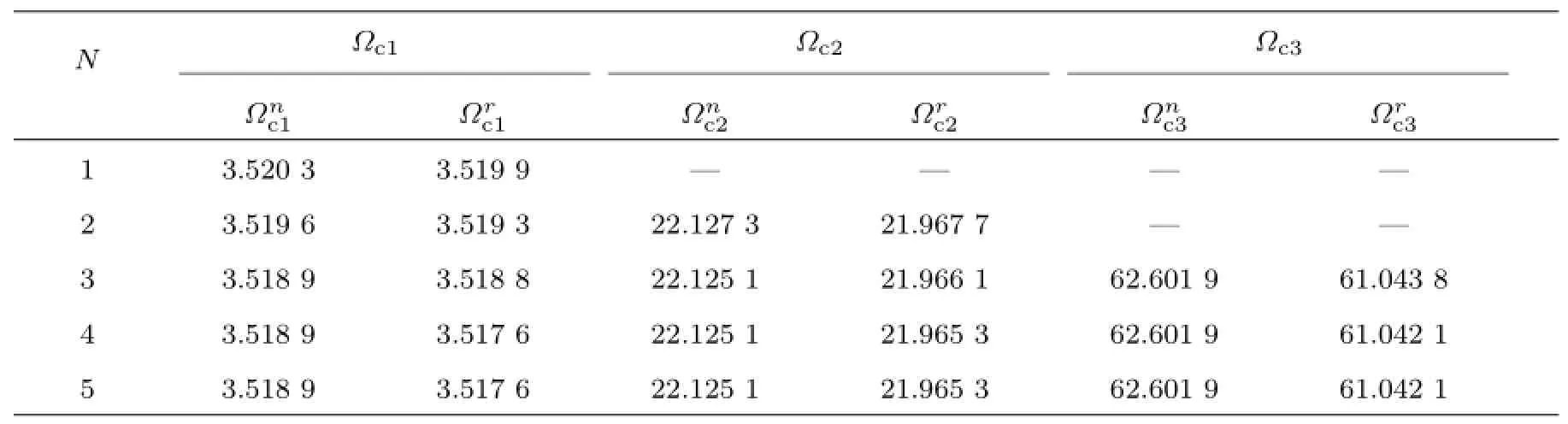
表3 临界转速的收敛性验证(l=20)

3 结论

本文给出悬臂旋转轴涡动频率和临界转速的经典分析解以及Galerkin近似解的求解公式和计算过程，旋转轴动力学模型基于考虑转动惯量和陀螺效应的Rayleigh梁理论建立。Galerkin过程分别采用转速无关不旋转Euler-Bernoulli悬臂梁振型函数和转速相关旋转Rayleigh悬臂梁振型函数。结果表明，Galerkin近似解具有较好的收敛性，仅保留3项不旋转振型函数或者仅保留4项旋转振型函数，即可得到收敛的涡动频率和临界转速。Galerkin近似解与经典解之间的差距很小，可以忽略不计。转速相关的旋转Rayleigh振型函数涉及非线性特征方程求解，计算过程复杂，而不旋转Euler-Bernoulli振型函数与转速无关，易于计算，为采用不旋转Euler-Bernoulli振型函数近似求解旋转悬臂轴动力学特性(例如，运用于包括镗、铣削连续刀杆切削系统的稳定性分析)和简化数值计算过程提供了依据。