行为m-NA 阵列的若干极限理论
2020-12-14王宽程高小明杨英钟
王宽程, 高小明, 杨英钟
(闽南理工学院 信息管理学院, 福建 泉州 362700)
Joag-Dev和Proschan[1]提出了下面的NA概念.
定义1 称随机变量X1,X2,…,Xn,n≥2是NA(negatively associated)的,若对任意2个非空不交子集A1,A2⊂{1,2,…,n}均有
Cov(f1(xi;i∈A1),f2(xj;j∈A2))≤0.
(1)
式中,fi,i=1,2是使式(1)有意义且对各变元不降的函数.
称随机变量列{Xn;n≥1}是NA列,如果对任意n≥2,X1,X2,…,Xn是NA的.
由于NA序列在可靠性理论、渗透理论和多元统计分析理论等均有广泛应用,从而引起许多学者的极大兴趣,例如文献[2-4]等.
Hu等[5]提出了如下m-NA 随机变量的概念.
定义2 设m≥1是一给定的整数,如果对任意n≥2和满足|ik-ij|≥m(1≤k≠j≤n)的任意i1,…,in,都有Xi1,…,Xin是NA序列,则称{Xn,n≥1}是m-NA(m-Negatively Associated)序列.
固定n,假设每一行内的随机变量序列{Xni}是m-NA,则称随机阵列{Xni;1≤i≤n,n∈}是行为m-NA 阵列.
显然NA序列是m-NA 序列在m=1时的特例. 由于m-NA 随机变量弱于NA随机变量,也就更弱于独立随机变量,从而引起了人们的广泛兴趣.近年来有关m-NA 序列收敛性的研究可见文献[6-9].但研究m-NA 随机阵列的文献却很少,本文研究m-NA 阵列的若干收敛性质,推广和改进了NA列和独立情形的弱大数定律、Lp收敛性和完全收敛性.
1 预备知识
称随机阵列{Xni;1≤i≤n,n∈}是p阶cesaro一致可积的,若
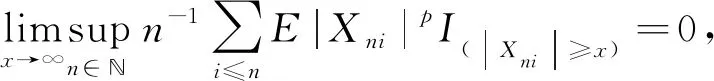
(2)
由文献[4]所述,式(2)等价于
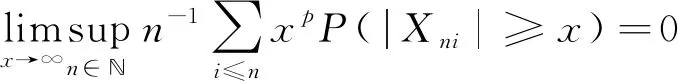
(3)
及
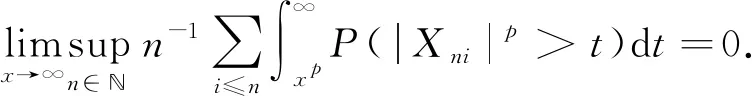
(4)
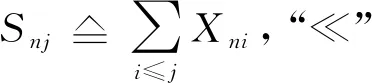
2 主要结果与证明
引理1[8]设{Xn;n∈}为m-NA 随机变量序列.若{fn;n∈}皆是单调非降(或者单调非增)连续函数,那么{fn(xn);n∈}仍然是m-NA 序列.
引理2[8]设{Xn;n∈}是均值为0的m-NA 序列,且对p≥1,有E|Xn|p<∞,那么∀n≥m≥1,若1≤p≤2,则
这里取Cm,p=4mp.
定理1 设{Xni;1≤i≤n,n∈}是行为m-NA阵列,且对1 定理1的证明: 取xn=n1/p,当n→∞时,xn→∞,对Xni截尾,记 故要证定理1,只需证Jn1→0,Jn2→0,n→∞.由引理2及Morkov不等式有 由式(3),且xn=n1/p得, 由式(3),∀ε>0,∃M,使当y>M时有 即当xn>M时,有 定理1证明完毕. 推论1 设{Xn;n≥1}是NA列,且对1≤p≤2,有 (5) 则 定理2 设{Xni;1≤i≤n,n∈}是行为m-NA阵列,且对1 定理2的证明 仍用定理1的记号,这里取xn=n(1-p/2)/4,因1 定理2证明完毕. 推论2 设{Xn;n≥1}是NA列,且对1 (6) 则 (7) 定理3 设{Xni;1≤i≤n,n∈}是行为m-NA阵列,且对1 定理3的证明 仍沿用定理1的记号,取xn=nα(2-p)/4,∀ε>0有 (8) 又因为xn=nα(2-p)/4,所以∃>0,使得当n≥时,有xn>M,则 同理可得 令t=z2/p,则有 由式(8)得 定理3证明完毕. 推论3 设{Xn;n≥1}是NA列,且对1 则对αp≥1,有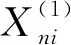
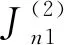
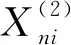
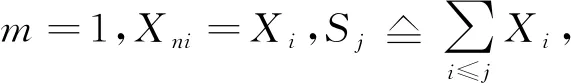
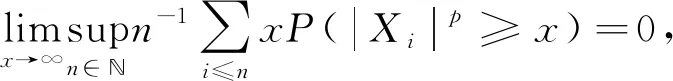
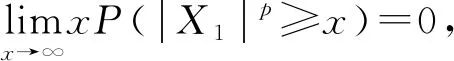
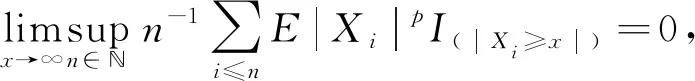
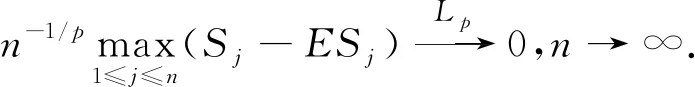
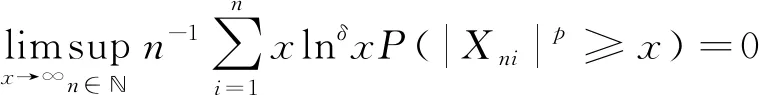
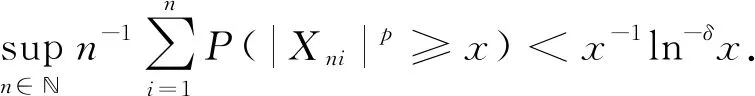
3 结 论
