q-二项式定理、q-高斯和公式及q-欧拉变换公式的概率证明

2020-11-02湖南环境生物职业技术学院刘现芳

数学大世界 2020年25期

湖南环境生物职业技术学院刘现芳

利用随机变量的期望值来证明一些重要定理，这种概率方法是数学领域的一个重要手段，并且在数论、代数、组合数学等数学领域已有比较成熟的研究，而在基本超几何级数中亦有许多重要应用。例如，在统计学领域里，Kadell[3]将Ramanujan’s1ψ1和实现了一种新的证明方式—概率证明，再比如，Fulman[1]利用Markov Chain 概率理论将Rogers-Remanujan 等式得到概率证明方法；而Chapman[2]在Fulman 的理论成果上加以研究，也用概率的方法推广证明了Andrews-Gordon 等式。

根据文[4][5]的研究成果容易知道，文章中构造了一个离散型随机变量X，并且根据随机变量提出了一个全新的概率分布W（x；q），如下：

满足：pn，k（x；q）＞0，Σpn，k（x；q）=1，x＜0，0＜q＜1，n=0，1，k=0，1，Λ。

利用上式概率分布，得到了q-二项式定理、q-高斯和公式的一个概率证明方法，并且得到了几个新的求和公式及变换公式。

随机变量的期望值是概率统计学中的一个非常重要的理论，如果我们假设存在离散型随机变量X，若它的概率密度函数为p（x），那么我们将E[X]作为随机变量X 的期望值的一个标记，其定义如下：

首先是知识准备，我们给出引理1、引理2 以及一些重要的知识概念：

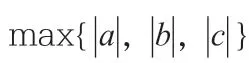
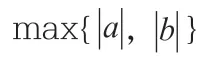
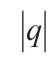
q-升阶乘的定义为：

并且，

q-二项式系数我们定义如下：其中任意的n，k ∈N，

q-升阶乘的乘积形式定义：

若任意的n，k ∈z+，有：

我们将上式级数rs[6][7]称为双边级数。

当s=r+1 时，Heine 将q-基本超几何级数r+1r 的定义如下：

如果s=r+1，而且qa1a2…ar+1=b1b2…br，我们称r+1r 这个基本超几何级数是平衡的（balanced）。

从Ramanujan’s1ψ1中可以导出一个Andrews-Askey 积分[9]：

其中，分母不含零因子。

最近，文[10]更进一步地推广了Andrews-Askey 积分，有如下形式：

其中，分母不含零因子。

文章的主要目的是利用给出的期望公式对q-二项式定理、q-高斯和公式进行简单的概率证明，并且利用引理3 推广的新q-积分公式证明了q-欧拉变换公式。

一、q-二项式定理

q-二项式定理是数学中的一个重要结论，并且广泛地应用在特殊函数、物理学、量子代数和量子统计学等科学领域。Cauchy、Heine[11]和Jacobi 就非终止型q-级数导出了q-二项式定理。此外，还包括许多q-二项式定理的证明方法。例如，Askey 利用有限差的方法更好更简便地给出了证明等。本小节，我们通过随机变量的期望值的计算，从而得到了q-二项式定理的一个简便证明方法。

定理1[6][7]q-二项式定理：

证明：在引理1 中，我们令c=0，有：

结合上式及引理2，容易得到：

因此，我们有：

即

将ab 用a 代换，可以得到：

q- 的高斯和公式在q- 级数中占有重要地位。1847 年，Heine[11]导出了q 化的高斯和公式；在组合数学理论基础上，Stanton 和Joichi 得到了q-高斯和公式的双射证明方法;Rahman和Suslov 利用一阶线性差分方程证明了q-高斯和公式。下面，我们利用概率方法对q-高斯和公式进行简单的证明。

定理2[6][7]q-高斯和公式：

在引理2 中，我们令a=0，有：

结合(23)和(25)两式，易得：

将c 用a 代换，b2用c 代换，易得：

由此，我们证明了q-高斯和公式。

注释1：我们对于q-二项式定理、q-高斯和公式的证明过程比文[5]的证明过程更简单。