黄晓琳

(福建省南安国光中学 362321)

笔者有幸参加了2019年高考数学科的阅卷工作，并全程参与对理科第21题评分细则的讨论与制定、阅卷教师的培训与指导、阅卷过程的三评与仲裁．结合考生的答卷情况，以及同侪之间的讨论，形成以下思考与同行们交流分享．

1 试题分析

2019年高考全国Ⅰ卷理科数学第21题：为了治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验．试验方案如下：每一轮选取两只白鼠对药效进行对比试验．对于两只白鼠，随机选一只施以甲药，另一只施以乙药．一轮的治疗结果得出后，再安排下一轮试验．当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有效．为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得-1分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得-1分；若都治愈或都未治愈则两种药均得0分．甲、乙两种药的治愈率分别记为α和β，一轮试验中甲药的得分记为X．

(1)求X的分布列；

(2)若甲药、乙药在试验开始时都赋予4分，pi(i=0,1,…,8)表示“甲药的累计得分为i时，最终认为甲药比乙药更有效”的概率，则p0=0，p8=1，pi=api-1+bpi+cpi+1(i=1,2,…,7)，其中a=P(X=-1)，b=P(X=0)，c=P(X=1)．假设α=0.5，β=0.8．

(i)证明：{pi+1-pi}(i=0,1,2,…,7)为等比数列；

(ii)求p4，并根据p4的值解释该试验方案的合理性．

高考是选拨性考试，压轴题在高考卷中起着区分考生数学水平的重要作用．今年压轴题的难度虽然不是太大，但由于交汇点新、综合性强，以及题序位置的客观因素，试题还是具有一定的区分功能．

1.1 考点分析

第(1)问计算随机变量的分布列是概率统计的常规题型．问题综合考查了独立事件、互斥事件、对立事件等基础知识，涉及数据处理、运算求解能力，渗透分类与整合思想．问题虽小但内涵丰富，对学生的基础性有全面的考查，不高的起点让一些低发展水平的学生也有一定的展示机会．

第(2)问给出一个常系数齐次线性递推数列，通过该数学模型计算概率，并分析其统计意义．问题综合考查了等比数列的定义、数列的通项与求和、小概率事件等数学知识，涉及数据处理、运算求解、推理论证及创新意识、应用意识等数学能力，渗透转化与化归、特殊与一般、或然与必然等数学思想．问题的解法多样，思维要求高，可以让较高发展水平的学生展示其才能．

1.2 试题特点

从题干角度看，选择了药品检验这一考生熟悉、相对公平的背景进行设计；条件涉及的数据较多、关系复杂；考虑到压轴位置，语言叙述相比往年简练．

从设问角度看，坚定概率统计为判断、决策服务这个应用方向；从知识到能力再到思想，三个问题的考查都具有很高的综合性；计算概率的递推数列模型较好地体现了创新性．

1.3 解题难点

首先是阅读理解方面．在考场的紧张状态下，特别是在压轴位置，要做到细致地阅读审题、冷静地思考分析，对考生的综合素质都是一个巨大的考验．

其次是运算求解方面．无论是第(1)问中涉及变量α,β的概率运算，还是第(2)问中大数值的数列项的求解，都对考生的运算求解能力提出较大的挑战．

最后是统计意义的解释方面．数据处理与数学运算不同，计算出的数据说明什么，即数据有何指导意义？如何用数据支撑阐述最终的判断与决策？这些都是学生有关概率统计学习，包括教师的教学需要突破的难点．

2 解答分析

本题零分卷与低得分卷占到半数以上，故实际呈现的解法并不多，暴露的问题也不够全面．但对有作答的考生的答卷进行分析，我们还是可以从中提炼出相关知识的教学与备考启示．

2.1 得分情况

经统计，某省总计131435份的理科答卷中，本试题的0分卷与1分卷合计58.28%；10分卷及以上合计0.7%；4分卷所占的比例最大，比例为14.9%．整体阅卷难度不大，产生的三评卷(占总阅卷量0.7%)及仲裁卷(占总阅卷量0.36%)比较少．

2.2 失分原因

第(1)问的主要错误有：由于审题不认真，混淆甲、乙的赋分规则；将甲的得分错看成甲、乙得分相加；将一轮测试后的得分错看成四轮测试后的得分；误将第(2)问中α,β的具体值用到第(1)问．由于知识理解不到位，导致独立事件、互斥事件的概率计算错误．

第(2)问的主要错误有：采用不完全归纳证明数列成等比；对递推关系式进行胡拼乱凑得到数列成等比．由于数列的首项、项数等基本量分析错误，或者等比数列的通项公式、求和公式记忆错误，导致最终结果计算错误；计算出概率值后不能正确解读其概率意义．

2.3 解法讨论

2.3.1第(2)问第(ⅰ)问解法分析

解法一由(1)得a=0.4,b=0.5,c=0.1，因此pi=0.4pi-1+0.5pi+0.1pi+1，即pi+1=5pi-4pi-1．

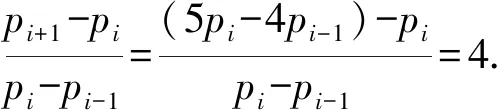
又因为p1-p0=p1≠0，

所以{pi+1-pi}(i=0,1,2,…,7)是首项为p1，公比为4的等比数列．

解法二由(1)得a=0.4,b=0.5,c=0.1，因此pi=0.4pi-1+0.5pi+0.1pi+1，

即pi+1=5pi-4pi-1．

分别取i=1,2,…,7时，

可得p2=5p1，p3=21p1，p4=85p1，p5=341p1，p6=1365p1，p7=5461p1，p8=21845p1．

则p2-p1=4p1，p3-p2=42p1，p4-p3=43p1，p5-p4=44p1，p6-p5=45p1，p7-p6=46p1，p8-p7=47p1，

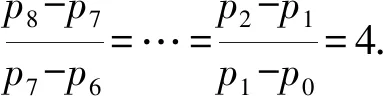
后同解法一．

解法二是注意到数列的项数有限，故可利用递推关系式，采用完全归纳的方法，获得p2到p8这7项与p1的关系，进而证明数列成等比．采用此法，计算量较大，但是一旦获得项间关系，最后一问的概率值也就唾手可得了．采用此法的考生不多见，原因可能是没有发现该数列为有限数列，或者时间与计算能力的限制．

解法三由(1)得a=0.4,b=0.5,c=0.1，因此pi=0.4pi-1+0.5pi+0.1pi+1，

即pi+1=5pi-4pi-1．

其特征方程为x2=5x-4，解得x1=1,x2=4．

令pn=a1·1n+a2·4n，

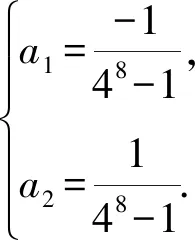
后同解法一．

解法三大都出现在满分卷中，这部分考生应该是有接受过竞赛辅导或培优训练．在识别出递推公式的模式下，自然而然地想到对应的解题套路．该法在证明等比中并不轻松，但是一旦获得通项后，最后一问的概率计算也就易如反掌了．

2.3.2第(2)问第(ⅱ)问解法分析

解法一由(i)得

pi+1-pi=(p1-p0)·4i=p1·4i，

故{pi+1-pi}(i=0,1,2,…,7)的前8项和等于

解法一从上一问等比数列的结论入手，通过公式获得p4,p8与p1的关系，有作答到此步的考生大部分采用此法，但不少考生由于基本量分析错误，或者公式记忆错误，导致最终计算出错误的结果．

解法二由(1)得pi+1=5pi-4pi-1，

分别取i=1,2,…,7时，可得p2=5p1，p3=21p1，p4=85p1，p5=341p1，p6=1365p1，p7=5461p1，p8=21845p1．

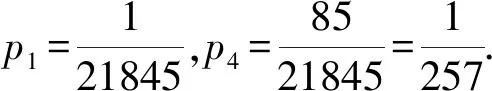
解法二是上一问解法二(完全归纳法)的自然延续，方法虽然略显笨拙，但在高考压轴题最后一问的位置，考生还能够认真审题发现数列有限，冷静细致地运算得到正确结果，这样强大的心理素质与计算能力还是值得肯定的．

解法三由{pi+1-pi}(i=0,1,2,…,7)为公比为4，首项为p1的等比数列．

(p8-p7)+(p7-p6)+(p6-p5)+(p5-p4)=p8-p4,

(p4-p3)+(p3-p2)+(p2-p1)+(p1-p0)=p4-p0,

解法三敏锐地发现p4,p8在数列中的位置，灵活采用等比数列的性质，回避p1的计算，直接建立p4,p8关系，快速获得最终结果，采用此法的考生凤毛麟角，屈指可数．

3 教学启示

3.1 研究解题方法的同时，要重视答题的严谨规范

数学学习离不开解题.通过形式多样的解题方法将不同的知识结点成线、连线成网，建构连贯一致的知识体系，达成对知识深度的理解；借助灵活多变的解题方法，将高深的思想具化落实、演化拓展，培养品质优良的数学思维，实现对数学能力的提升．解题要重视研究方法技巧，也要重视答题的严谨规范，这是应试的要求，也是素养的体现．

数学语言是规范的．阅卷是时候，我们发现很多不规范、不科学的符号书写，比如将α，β写成a，p，甚至写成4，9从而导致后面计算错误的．不规范的书写可能源于教师错误的示范，也可能是学生自身不良的书写习惯．培养规则意识是数学教学的一个重要任务，不按规范书写约定俗成的科学符号，就是没有规则意识的一种表现，不讲规则是要付出代价的.

逻辑推理是严谨的．阅卷之前讨论评分细则时，我们就预设了第(2)问等比数列证明时p1-p0≠0的证明方法，即采用反证法进行证明(证明略)．但在实际阅卷过程中，我们发现几乎所有学生对该问题都没有说明(更不用说证明)．笔者抽检了大部分该题满分卷考生的答卷，也未发现有考生给出严格的证明．逻辑推理的严谨与否体现了数学思维品质的高低，反映了学生核心素养发展的水平，因而在教学必须给于足够的重视．

3.2 提炼解题模式的同时，要注重对知识本质的理解

在数学学习的过程中，通过教师或学生自身提炼一定的解题模式，对解题时联系新旧问题、启发解题方向、缩短思维过程、提高解题速度有很大的帮助．但是在教学中，如果忽视解题模式的提炼过程，不注重对知识本质的理解，机械的对题型、套解法，势必会导致思维僵化，产生定势．

怎么做重要，这样做是为什么也很重要．如上所述，本题第(2)问的解答，从实际呈现的答卷来看，大多数的考生首先想到的不是等比数列的定义，而是递推关系式的构造与变形．在对各种构造的本质不理解的情况下，光凭外在的形式去套题型，答卷呈现的是一堆胡拼乱凑的式子．这与2018年高考全国Ⅰ卷理科数学第16题“已知函数f(x)=2sinx+sin2x，则f(x)的最小值是______．”有类似的地方，学生拿到该题，首先想到的不是函数最值的分析，而是三角函数的题型模式与变形套路，在二次模型换元法套路、y=Asin(ωx+φ)+K模型恒等变换套路这些模型套路对不上号的情况下，考生就束手无策了．这会不会是我们解题训练中，过度模式化、套路化、技巧化惹的祸？

怎么做重要，得到的结果有什么用也很重要．统计数据的计算不是目的，目的是计算出来的数据说明什么，要帮助我们做什么样的判断与决策，学生对这方面的思考还不是很深刻，这是不是与我们教学中只重视计算套路与技巧，忽视数据背后统计意义分析有关？本题最后一问仅有不到0.3%的考生能够在正确计算结果的情况下作出恰当的概率解释．可见绝大部分考生对小概率事件知识并没有真正的理解．小概率事件相关知识在正态分布的3σ原则、独立性检验等处均有涉及，教学中我们应该采用什么样的方法，通过什么样的形式，将相关的原理解释给学生，这些都是在统计运算之外，应该着重关注的方向．

3.3 强化解题训练的同时，要关注反思习惯的养成

知识的理解、思维的训练、能力的提升、素养的发展都离不开解题，高考的评价方式也要求学生需要进行一定难度及强度的解题训练．阅读、计算、作图、表达这些解题的基本功，都需要通过严格而又艰苦的解题训练才能得以夯实．学而不思则罔，思而不学则殆．解题的实践与解后的反思两者不可偏废．

概念的深刻理解，除了解题中正例的不断强化，也需要经常反思一些典型的错例、反例、特例．对于本题第(2)问等比数列的证明，很多考生之所以忽视对首项不为零的说明，一部分原因就是学习过程中，我们强调得多的是“什么是？为什么是？”，而弱化了对“什么不是？为什么不是？”的反思．