张 蕾,王 燕,杨玉军

(烟台大学数学与信息科学学院, 山东 烟台 264005)

在图论中, 图的特征值和特征向量通常指的是其邻接矩阵的特征值和特征向量[1-2]. 众所周知, 连通k-正则图(任意点的度是k)的任一特征值λ满足|λ|≤k, 而且k是单特征值. 相似地, 连通k-正则二部图的任一特征值μ满足|μ|≤k, 而且k和-k都是单特征值. 点传递图是一类正则图. 那么, 一个点传递图除了它的度数之外还有没有单特征值? 或者说, 如何确定一个点传递图除去它的度数之外的单特征值? 在文献[3]中, PETERSDORF和SACHS给出了点传递图单特征值的范围, 但是对于具体的点传递图还需要根据图本身的特点来确定它的单特征值. 本文研究了一类特殊的点传递图-凯莱图的单特征值. 假定G是有限群,S是G的子集. 如果S不含单位元, 逆封闭, 并且可以生成G, 则称S是G的一个凯莱子集. 此时,G关于S的凯莱图记作Cay(G,S), 其中,Cay(G,S)的点集是G中的元素; 任意两点g,h(g,h∈G)相邻当且仅当hg-1∈S[4-6]. 本文重点讨论了循环群凯莱图(循环图)和二面体群凯莱图的单特征值. 在第2、3 节中, 分别给出了循环群和二面体群凯莱图的单特征值需要满足的必要条件. 一般来说, 这些必要条件不是充分条件, 针对这一情况给出了一些例子.

1 基础知识

定义1(右循环矩阵)R=(rst)n×n是一个n×n矩阵,如果R的第s行是R的第一行向右平移s-1步得到的, 那么称R是右循环矩阵. 也就是说,R中的元素满足rst=r1,t-s+1. 其中,R的下标属于{1,2,…,n}且模n运算. 为了在以后的叙述中更加方便, 用[r1,r2,…,rn]R表示R, 其中,rm(1≤m≤n)是R的第一行元素.

定义2(左循环矩阵)L=(lst)n×n是一个n×n矩阵, 如果L的第s行是L的第一行向左平移s-1步得到的, 那么称L是左循环矩阵. 也就是说,L中的元素满足lst=l1,s+t-1. 其中,L的下标属于{1,2,…,n}且模n运算. 为了在以后的叙述中更加方便, 用[l1,l2,…,ln]L表示L, 其中,lm(1≤m≤n)是L的第一行元素.

注意:在图论中, 循环矩阵通常指的是右循环矩阵. 在本文中, 为区分这2种平移方式得到的矩阵, 分别定义了左循环矩阵和右循环矩阵. 然而, 这2种循环矩阵之间也有一定的联系.

引理1 令L是左循环矩阵, 那么L2是右循环矩阵.

证明令L=(lst)n×n,L2=(ast)n×n. 那么

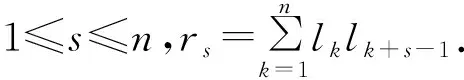
已知, 右循环矩阵的特征值可以用其矩阵的元素表示出来.

引理3令R=[r0,r1,…,rn-1]R是右循环矩阵,那么R的特征值为

其中, i是复数, i2=-1.

在文献[3]中,作者给出了点传递图单特征值的一个描述.

引理4令Γ是连通k度点传递图,λ是Γ的单特征值. 如果Γ有奇数个顶点, 那么λ=k; 如果Γ有偶数个顶点, 那么λ=2α-k. 其中, 0≤α≤k.

由于连通正则图的度一定是它的单特征值,而且连通正则二部图的负度数也是单特征值,而点传递图都是正则图,所以根据引理4, 我们只需要确定偶数个顶点的点传递图的单特征值.

2 循环图的单特征值

在图论中, 循环图通常定义为邻接矩阵是循环矩阵的图. 实际上循环图也可以定义为循环群的凯莱图. 因此, 循环图是点传递图.

令G=是2n阶循环群,S是G的凯莱子集. 假设A是Cay(G,S)的邻接矩阵, 那么A=[0,a1,…,a2n-1]R是右循环矩阵, 其中对任意1≤j≤ 2n-1,aj=1当且仅当gj∈S. 否则为0. 由凯莱子集的定义知,aj=a2n-j.

定理1 令G=是阶为2n的循环群,S是G的凯莱子集且|S|=k. 假设A=[0,a1,…,a2n-1]R是Cay(G,S)的邻接矩阵. 如果λ是A的单特征值并且λ≠k, 那么λ=2α-k.其中，当n是偶数时,α=2(a2+a4+…+an-2)+an. 当n是奇数时,α=2(a2+a4+…+an-1). 进一步说, 在这2种情况下,α≠k.

证明根据引理3,A的特征值可以表示为:

也就是说

ancos(tπ),0≤t≤2n-1.

(1)

易知, 对任意的1≤j≤n,λj=λ2n-j. 因此, 只有λ0和λn可能是单特征值. 通过进一步计算可知,λ0=k,λn=-2a1+2a2+…+2an-1cos(n-1)π+ancosnπ. 因此, 当n是偶数时,λn=2[2(a2+a4+…+an-2)+an]-k, 此时α=2(a2+a4+…+an-2)+an; 当n是奇数时,λn=2[2(a2+a4+…+an-1)]-k. 此时α=2(a2+a4+…+an-1).

注1根据定理1, 阶为2n的循环群, 除去它的度外至多有1个单特征值. 然而, 一般情况下无法确定一个图在什么情况下一定含有2个单特征值, 因为λn可能与某些λi(i≠n)相同.现在把公式(1)分成以下4种情况.

推论1在定理1中,如果对任意的1≤j≤n-1, 我们要求aj=an-j, 那么当n是奇数时, 循环图Cay(G,S)恰有1个单特征值(也就是它的度).

证明由定理1和注1中的第4个公式可知.

推论2在定理1中,如果n是大于3的素数并且至少存在一个j(1≤j≤n-1), 使得aj≠an-j, 那么该循环图有2个单特征值.

推论3在定理1中,如果n是不能被3整除的奇数, 并且对任意的1≤j≤n-1, 有an≠an-j, 那么该循环图有2个单特征值.

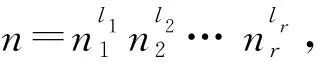
下面将选取几个阶为2n的循环群的凯莱子集, 解释单特征值的复杂性.

例1令G=是阶为2n的循环群.如果n是偶数,取S={g,g2,g3,g-1,g-2,g-3},那么循环群Cay(G,S)恰有1个单特征值,也就是它的度6.

通过相似的证明方式,给出下面的例子.

例2令G=是阶为2n的循环群.

(1)如果n是不能被3和4整除的偶数,取S={g,g2,g-1,g-2}, 那么循环群Cay(G,S)有2个单特征值.

(2)如果n是3的倍数, 取S={g,g2,g-1,g-2}, 那么循环群Cay(G,S) 恰有1个单特征值.

(3)如果n是奇数且是3的倍数, 但它不是9的倍数, 取S={g,g3,g-1,g-3}, 那么循环群Cay(G,S)有2个单特征值.

3 二面体群凯莱图的单特征值

令Dn={θ,τ|θn=τ2=1,τθτ=θ-1}是阶为2n的二面体群. 根据Dn凯莱子集选取的不同, 把这一节分成2种情况讨论.

情况1令S={τ,τθu,τθv,…,τθw}是Dn的凯莱子集,S中有k个元素, 易知凯莱图Cay(Dn,S)是一个二部图. 因此,Cay(Dn,S)的邻接矩阵可记作

(2)

其中,A1,A2和2个零矩阵都是阶为n的方阵. 当1≤r≤n,n+1≤s≤ 2n时, 若θr-1与τθs-n-1相邻, 那么(A1)rs为1, 否则为0. 当n+1≤r≤ 2n,1≤s≤n时, 若τθr-n-1与τθs-1相邻, 那么(A2)rs为1, 否则为0. 易知A1=A2并且它们都是左循环矩阵. 记A1=A2=B=[b0,b1,…,bn-1]L，那么，

(3)

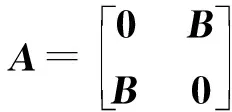
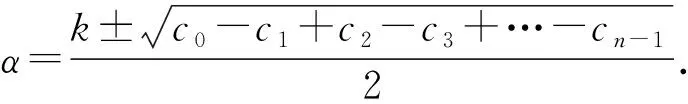
|λI-A|=|λI-B||λI+B|=|λ2I-B2| .

那么A的特征值是由B和-B的特征值组成的. 或者说, 如果知道B2的特征值, 就可以得到A的特征值.由引理3知,B2的特征值是

如果n是奇数, 那么B2只有一个单特征值μ0=c0+c1+…+cn-1. 由引理2知μ0=k2. 由于k是凯莱图的度, 可知当n是奇数时,A有2个单特征值k和-k.

如果把它写成2α-k的形式, 那么

与定理1的证明类似, 如果c0-c1+c2-c3+…-cn-1=k2, 那么可以得到b0=b2=…=bn-2=0或者b1=b3=…=bn-1=0. 无论哪种情况, 所得凯莱子集都无法生成整个群. 因此, 2α-k≠±k.

例3令Dn={θ,τ|θn=τ2=1,τθτ=θ-1},

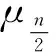
情况2取S为Dn的凯莱子集, 如果τθi∈S, 那么τθn-i∈S. 考虑Cay(Dn,S)的邻接矩阵P, 把P分成4块

(4)

其中,Pi(1≤i≤ 4)是阶为n的方阵. 当1≤s,t≤n时, 若θs-1与θt-1相邻, 则(P1)st=1, 否则为0; 当1≤s≤n,n+1≤t≤ 2n时, 若θs-1与τθ2n-t+1相邻, 则(P2)st=1, 否则为0; 当n+1≤s≤ 2n,1≤t≤n时, 若τθ2n-s+1与θt-1相邻, 则(P3)st=1,否则为0; 当n+1≤s,t≤ 2n时, 若τθ2n-s+1与τθ2n-t+1相邻, 则(P4)st=1, 否则为0.

由凯莱图的邻接关系可知, 在P1中2个点θs-1和θt-1相邻当且仅当θs-t∈S. 易知这一邻接关系与在P4中相同, 也就是说P1=P4. 相似的,P2=P3. 进一步说, 容易证得这4个块都是右循环矩阵. 因此, 把P记作

(5)

其中,A=[0,a1,…,an-1]R,B=[b0,b1,…,bn-1]R都是(0,1)—矩阵. 由凯莱子集S选取的要求可知, 对1≤k,m≤n-1, 有ak=an-k,bm=bn-m.

P的特征多项式为

|λI-(A+B)|·|λI-(A-B)| ,

(6)

因此,P的特征值是由A+B和A-B的特征值组成的.如果想得到P的单特征值,就只需要求得A+B和A-B的单特征值. 由于A+B和A-B都是右循环矩阵, 其中,A+B=[b0,a1+b1,…,an-1+bn-1]R,A-B=[-b0,a1-b1,…,an-1-bn-1]R. 那么由引理3, 可以得到接下来的引理5.

引理5由上文给出的定义得到Dn,S和P.如果把A+B和A-B的特征值记作λt和μt(1≤t≤n), 那么P(或凯莱图Cay(Dn,S))的特征值为

…+(an-1+bn-1)ωtn-1,

以及

…+(an-1-bn-1)ωtn-1,

(i)当n是奇数时,

(ii)当n是偶数时,

其中, 0≤t≤n-1.

证明已知,Cay(G,S)的单特征值形如2α-k(1≤α≤k). 由引理5知:

当n是奇数时, 易知对任意的1≤t≤n-1, 有λt=λn-t,μt=μn-t. 那么在这种情况下,λ0=k和μ0=-b0+(a1-b1)+(a2-b2)+…+(an-1+bn-1)是Cay(G,S)的2个单特征值. 可以求得,α=k或a1+a2+…+an-1.

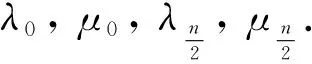
注3在定理3中, 只给出了λ是单特征值的必要条件, 但它未必是充分条件.

例4令Dn={θ,τ|θn=τ2=1,τθτ=θ-1}是二面体群.

(2)如果n是不能被3和4整除的偶数, 取S={θ,θ-1,τθ3,τθ-3,τθ5,τθ-5}, 那么对应的凯莱图有4个单特征值.

注4 对于一般的二面体群, 如果不对它的凯莱子集加任何条件, 就没有好的办法求出它对应的凯莱子集的单特征值.

接下来, 通过一个简单的例子来说明一般情况下的单特征值的复杂性.

例5令D5={θ,τ|θ5=τ2=1,τθτ=θ-1},取S={θ,θ4,τ,τθ,τθ2}, 那么Cay(D5,S1)恰有一个单特征值, 也就是它的度5. 取S2={θ,θ4,τ}, 那么Cay(D5,S2)除去它的度3外还有一个单特征值1.

4 结束语

本文通过循环图特征值的算法以及H.SACHS和M.PETERSDORF对点传递图特征值的归纳, 给出了循环群和两类二面体群单特征值求得的必要条件, 并给出了该必要条件不是充分条件的一些例子.