江苏省南京市第十二初级中学 李正球

每次考试过后，总有教师埋怨：这个因式分解题平时都练过好几次了，可还是有许多学生不会做或做错！那个平面几何对称性问题，只是将作业题中图形的位置改变了一下，怎么还是有好多人做不出！于是，教师往往怀疑学生的学习能力，甚至认为，有些学生根本不是学习的料儿，大有“朽木不可雕也”之嫌.于是问题来了，学生每天坐在教室里，说辛苦真的很辛苦，可辛苦之后却收获不大.难道他们真的不会学习？还是教师的引导出了问题？在笔者看来，学生如何学固然重要，但从教师教的角度看，教师的责任更大.学生出错，往往是对课堂上所学的知识一知半解所致，要彻底改变这种想象，必须要让学生学会深度学习.所谓数学深度学习，即要求学生真正感悟数学，领会数学，善于发现数学学科内部的规律，从而自觉地利用这些规律去解决数学问题.笔者认为，学生的深度学习，离不开教师的引领，脱离了教师引领，学生的学习只能浮于表面，既达不到广度，更达不到深度.因此，教师教学中引导学生深度学习，应在知识的广度上和深度上做足文章.

一、由点连线，构建知识的完整性

一知半解是学习的大忌，尤其是数学这门学科.产生这种现象的根本原因在于，学生所学的知识往往是孤立的、零散的，因而，考试时，不会把相关知识串联起来.比如，见到矩形的四边中点的连线是菱形，却不知道等腰梯形的四边中点的连线也是菱形.遇到相关问题，学生只会回忆以前有没有遇到这道题，遇到的或许会做，没有遇到的就自然不会做了.这种思维僵化的根本原因，是在学习中只能看见一道一道题，即一个一个点，却看不到一个一个点背后的一条线，缺乏对知识的完整性与系统性的构建.因此，在初中数学教学中，教师要引导学生深度学习，首先应教会学生从每天做的题目出发，由点连线，构建知识的完整性.

比如，实数是初中数学的基石，初中数学的许多问题与实数有关，比如，研究一元二次方程的实数解，在实数范围内因式分解，实数比大小问题等，这就要求学生从整体上认识实数.或许，有的教师认为，实数就是有理数与无理数的统称，没有必要大做文章.其实，这种看法高估了学生，有一次我问一名学生，π是什么数？他回答“π是3.14”.我接着问，3.14是什么数？他回答“是无限小数”.我再问“无限小数是有理数还是无理数”，他就犹豫了，想了很大一会儿，回答说“是有理数”.然后我又问“那π是有理数吗”，他又犹豫了，还是旁边一名学生回答得干脆——“π是无理数”.于是产生了一对矛盾：π是3.14，是有限小数，却是无理数.这名学生的脸上一片茫然.而产生这种错误的认识的真正原因，其实是这名学生平时只看到一个一个数，却没有去关注数其实是个体系，于是会犯“一叶障目”或者“只见树木不见森林”的错误.可见，引导学生建立知识体系是何等重要.

其实，初中数学的每一块核心内容都是一个完整的知识体系，如实数体系，代数式体系，平面几何体系，函数体系，方程体系，概率与统计体系等，教师应该引导学生从整体上把握住各体系的结构，由点连线，才能使学生深刻把握住课本知识.

二、由浅入深，锻炼思维的深刻性

数学，是思维的体操.学习数学，可以让人明智，因此，由浅入深，锻炼思维的深刻性显得尤为重要，而思维的深刻性，从来不是与生俱来的，需后天培养，需要教师引导.在数学课堂教学中，如果教师只注重知识的传授，而不注重能力的培养，学生的思维往往只停留在表层，遇到稍有点难度的问题，他们往往或畏缩不前，或知难而退.因此，学生的深度学习，必须要有问题载体，需要教师对问题的预设.在数学课堂上，教师可以设计探究性问题，由浅入深，在系列问题的解决中，锻炼学生思维的深刻性.问题应源于课本，但不囿于课本.

如一元二次方程的根与系数的关系，即韦达定理，无论是在中考还是未来的高考中，都有着广泛的应用，这是培养学生思维深刻性的极好素材.在教学中，笔者设计了如下问题引导学生探究：

问题1：方程（1998x）2-1997×1999x-1=0的大根为a，方程x2+1998x-1999=0的小根为b，求a-b的值.（答案：a=1，b=-1999，a-b=2000）

问题2：已知a≥0，m2-2am+2=0，n2-2an+2=0，m≠n，求（m-1）2+（n-1）2的最小值.（答案：-2.提示：m、n是关于x的方程x2-2ax+2=0的两个根，根据根与系数的关系可得m+n=2a，mn=2，将代数式用完全平方公式展开，再根据完全平方公式恒等变形为（m-1）2+（n-1）2=m2-2m+1+n2-2n+1=（m+n）2-2mn-2（m+n）+2，然后整体代入，根据代数式极值的算法得出答案）

问题3：已知方程2x2-9x+8=0，求作一个二次方程，使它的一个根为原方程两根和的倒数，另一根为原方程两根差的平方.（答案：36x2-161x+34=0）

问题4：设x2-px+q=0的两实数根为α、β.

（1）求以α3、β3为两根的一元二次方程；（答案：x2-p（p2-3q）x+q3=0）

（2）若以α3、β3为根的一元二次方程仍是x2-px+q=0，求所有这样的一元二次方程.（答案：x2-2x+1=0，x2+2x+1=0，x2=0，x2-x=0，x2+x=0，x2-1=0）

问题来源于课本，问题的设计应从学生的认知水平出发.上面四个问题紧紧围绕韦达定理，难度呈上升趋势，可以让学生的思维螺旋式上升，问题探究过程中，学生的思维完成质的飞跃.有道是，玉不琢，不成器；人不学，不知道.教师应充分相信学生，积极创设问题引导学生，才能让学生的思维越走越远.

四、由此及彼，助推思维的广阔性

数学知识从来不是孤立存在的，无论是数学知识，还是数学方法，它们互相联系，互相作用，才支撑起这个“数学大世界”，这一点必须让学生明白，这其实也是辩证唯物主义的观点，体现了科学的方法论.前面说到，教师在教学中，引导学生构建了各个知识体系，运用问题培养学生思维的深刻性，教师还应引导学生沟通各知识体系间的联系，尤其是在解题方法的引导上，要打破常规，一题多解，代数问题几何化，几何问题代数化，引导学生从不同角度、不同侧面审视数学问题，这样才能使他们进入“广阔的思维空间”.

例如，如图1，过正方形ABCD的顶点C，任作一直线与AB、AD的延长线分别交于点E、F.求证：AE+AF≥4AB.

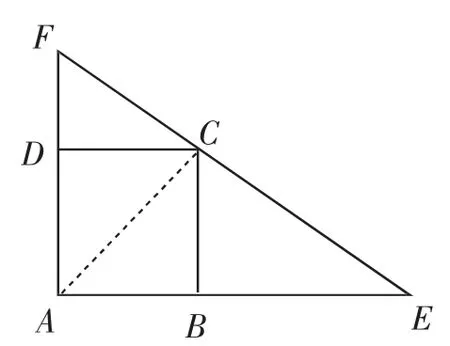
图1

本题是“形”的问题，但直接从“形”入手较难解决，若将“形”转化为“数”，则结论变为（AE+AF）2-4ABx×（AE+AF）≥0.则可联想起一元二次方程根的判别式，从而把它转化为“数”的问题来解决.对这类问题的探讨，可以帮助学生沟通代数与几何之间的联系，帮助他们树立科学的解题观.

又如，已知实数x、y、z满足x=6-y，z2=xy-9，求证：x=y.

本题本质上是个方程问题，可以将条件变形成x+y=6，xy=z2+9，于是引导学生将问题转化为一元二次方程题，尝试利用根的判别式加以解决.

证明：因为x+y=6，xy=z2+9，所以x、y是二次方程t2-6t+（z2+9）=0的两个实根，于是这个方程的判别式Δ=36-4（z2+9）=-4z2≥0，即z2≤0.因z为实数，显然应有z2≥0.要使两式同时成立，只有z=0，从而Δ=0，故上述关于t的二次方程有等根，即x=y.

由此及彼，体现了数学思维的灵活性，更体现了数学思维的广阔性.在学习中，学生的思维经常受阻或凝固，其实也无可厚非，只要教师积极引导他们及时调整思维角度，就可打通思维关节，将所谓的难题一网打尽.

引领学生深度学习，教师应注重教学的每一个细节.当深度学习既成为教师教学的一种常态，又成为学生学习的一种习惯时，学生的学习效率必然有一个质的变化，倘若如此，每次考试后，看到的必然是一张张笑脸，而教师的抱怨声也将成为“过去式”.