谢汉星，宋传静，2*，张佳凝，吴雪琰，沈晶蓉

（1.苏州科技大学数理学院，江苏苏州215009；2.南伊利诺伊大学卡本代尔分校机械工程与能源工艺系，美国伊利诺伊州62901）

经典力学经历了牛顿力学、Lagrange力学、Hamilton力学和Birkhoff力学，其中Birkhoff力学可以用于Hamilton力学、Lagrange力学和牛顿力学，同时也可用于统计力学、量子力学、强子物理、原子分子物理、生物物理、工程等领域。因此，Birkhoff力学在理论上具有高度的概括性。

1695 年，在Leibniz和L’Hospital的通信中，Leibniz提出了将微分阶次从整数变为分数后的含义问题。自此，分数阶微积分成了一门持续发展的学说。最近，分数阶微积分出现一个拓广研究，即导数的阶不再是常数，而是一个依赖于时间的函数[1-2]。这时的分数阶微积分称为变阶分数阶微积分。分数阶微积分概念的广义化使其能够更广泛地应用于某些阶数含有时间、位置、频率或位矢的复杂系统。为了解决实际问题，学者们已给出多种具有理论和实际意义的变阶分数阶算子。因此，对于变阶分数阶微积分理论及应用的研究是必要的。已有的关于变阶分数阶微积分的性质及应用可参阅文献[3-7]。

特别地，学者们对变阶分数阶的变分问题也进行了研究，并得到了变阶分数阶力学系统的运动微分方程[8-11]，如变阶分数阶Euler-Lagrange方程[9]、变阶分数阶Birkhoff方程[11]等。2013年，Odzijewicz、Malinowska和Torres[12]首次研究了变阶分数阶Lagrange系统的Noether定理。2016年，严斌和张毅[11，13]讨论了变阶分数阶Birkhoff系统的Noether定理。考虑到对称性的摄动与绝热不变量也是分析力学的一个重要研究方向[14-20]，笔者将研究变阶分数阶广义Birkhoff系统对称性的摄动与绝热不变量问题。首先，简述变阶分数阶导数的定义及基本性质；然后，考虑变阶分数阶广义Birkhoff系统对称性的摄动与绝热不变量，给出文中的主要内容；最后，举例说明结果的应用。

1 变阶分数阶导数

该节简单列出变阶分数阶导数的定义及其基本性质[9，11-12，21]。

设f（t）在区间[t1，t2]上连续且可积，则Riemann-Liouville变阶分数阶导数和Caputo变阶分数阶导数分别定义为

其中，Γ（·）为Gamma函数，0＜α(·，·)＜1，文中设α（t，τ）＝α（t－τ），α（τ，t）＝α（τ-t），0＜α＜1且为常数，t，τ∈[t1，t2]。

当α(·，·)→α时，（1）式至（4）式退化为

（5）式至（6）式即为左右Riemann-Liouville分数阶导数，（7）式至（8）式即为左右Caputo分数阶导数。

当α(·，·)→1时，则有

当f（t）在t＝t1点为零时，有

2 绝热不变量

设力学系统的位形由2n个Birkhoff变量aμ=aμ（t）描述且aμ（t1）=0，则Caputo变阶分数阶广义Birkhoff方程为[11]

其中，B（t，av）为Birkhoff函数，Rμ（t，av）为Birkhoff函数组，Λμ（t，av）为广义力，μ，v＝1,2，…，2n。

设时间和坐标的无限小变换为

在无限小变换（12）下，Caputo变阶分数阶广义Birkhoff系统（11）的对称性与守恒量问题已有讨论[11]，见如下定理1。

定理1对于Caputo变阶分数阶广义Birkhoff系统（11），如果存在规范函数（t，av）使得无限小生成元、满足

则该系统存在如下形式的守恒量

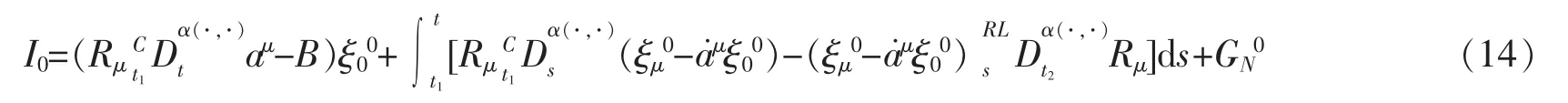
然而，当系统受到小扰动作用时，原有的守恒量也可能会发生变化。下面将基于Caputo变阶分数阶导数研究广义Birkhoff系统Noether对称性的摄动与绝热不变量。

首先，给出绝热不变量的定义：

定义1若是力学系统的一个含有小参量ε的最高次幂为z的物理量，且d Iz/d t正比于εz+1，则称Iz为基于Caputo变阶分数阶导数的一个z阶绝热不变量。

设系统受到的小扰动作用为εQμ，即

假设系统受到小扰动作用后的变化是在系统未受扰动的基础上发生的，则受扰动后的规范函数GN及无限小生成元ξ0、ξμ，可以表示为

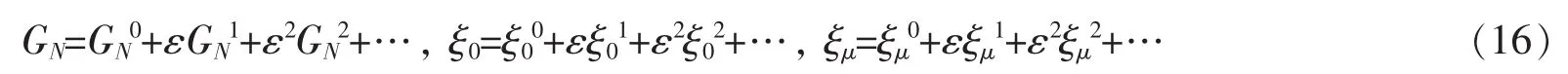
此时的无限小变换可以表示为

于是有

定理2对于受到小扰动作用的变阶分数阶广义Birkhoff系统（15），如果存在规范函数GNj使得无限小生成元满足

则该系统存在一个z阶绝热不变量

证明由（15）式和（18）式可得

证毕。

显然，z=0是一个特例，此时的绝热不变量称为精确不变量，其实质就是定理1中的守恒量。

定理2是文中的主要定理。实际上，变阶分数阶Birkhoff系统的绝热不变量、分数阶广义Birkhoff系统的绝热不变量及经典广义Birkhoff系统的绝热不变量均可由定理2退化而得，具体如下。

当Λμ＝0时，由定理2可得如下变阶分数阶Birkhoff系统的绝热不变量：

定理3对于受到小扰动作用的变阶分数阶Birkhoff系统

则该系统存在一个z阶绝热不变量

当α(·，·)→α时，由定理2可得如下分数阶广义Birkhoff系统的绝热不变量：

定理4对于受到小扰动作用的分数阶广义Birkhoff系统

则该系统存在一个z阶绝热不变量

定理4与文献[22]中的定理22给出的结论一致。

当α(·，·)→1时，由定理2可得如下经典广义Birkhoff系统的绝热不变量：

定理5对于受到小扰动作用的经典广义Birkhoff系统

则该系统存在一个z阶绝热不变量

定理5与文献[23]给出的结论一致。

3 举例说明

Birkhoff函数、Birkhoff函数组及广义力分别为

试基于Caputo变阶分数阶导数研究该系统的对称性摄动与绝热不变量。

变阶分数阶广义Birkhoff方程（11）给出

由（13）式可得

经计算

是（31）式的一个解。那么，由（14）式可得系统的精确不变量为

设系统受到如下的小扰动作用

则（18）式给出

解（35）式可得

那么，由定理2可得

当α→1时，由（37）式可得

（38）式为经典广义Birkhoff系统中的一阶绝热不变量。

进一步可求得系统的更高阶绝热不变量。

4 结语

首先列出Caputo变阶分数阶广义Birkhoff方程，然后基于绝热不变量的定义，研究了变阶分数阶广义Birkhoff系统的对称性摄动与绝热不变量。作为特例，还讨论了受到小扰动作用的变阶分数阶Birkhoff系统、分数阶广义Birkhoff系统和经典广义Birkhoff系统的对称性摄动与绝热不变量。文中的定理2、定理3为新结论，定理4、定理5与已有的结论是一致的。

力学与数学的交缘，尤其是分析力学与微分方程的交缘，促进了两个学科的发展。而且分析力学里发展出来的独特的积分方法，可用于一般微分方程的积分，只要将微分方程化为力学系统里的运动微分方程即可。而对称性的摄动及绝热不变量与力学系统的可积性之间有着密切的关系，因此，在力学系统中研究对称性的摄动与绝热不变量是很有必要的。