有记忆项的弱退化波方程的精确零能控性
2019-08-17刘瑞娟
刘瑞娟
(山西大学 数学科学学院, 太原 030006)
本文研究有记忆项的弱退化波方程的精确零能控性:
(1)
退化偏微分方程具有可变耗散系数算子,使得方程在空间区域上是不一致的,而且退化可以发生在边界的一部分,也可以发生在空间区域的子流形上,这使得研究这一类偏微分方程的精确能控性问题比较困难。 为了克服这一难点, 近年来研究退化偏微分方程的能控性问题,常用的方法有乘子法、矩方法、Carleman 估计等。
退化抛物型方程的控制问题在近10年来得到了广泛的关注,已经有很多研究结果[1-6],但目前为止对退化波方程的研究比较少。文献[7]利用HUM(hilbert unique method) 推导出退化波方程utt-(a(x)ux)x=0的狄利克雷边界精确能控性,其中波的传播速度a(x)称为耗散系数。对于更一般的情形,即a(x)=xα, 文献[8]通过对相应椭圆算子的谱来处理相关矩问题,推导出其对偶系统的能观测性不等式,证明了退化波方程utt+(xαux)x=0在退化点x=0处的狄利克雷边界精确能控性结果。 然而,在物理意义下,退化波在端点x=0处的传播速度为0,若控制作用在该点上,那么它对整个波几乎没有影响。 但是当作用在非退化边界时,对整个波的影响是持续的。 基于此,文献[9]利用文献[7-8]的方法证明了控制作用在非退化边界时的精确能控性问题。
对于有记忆的非退化波方程, 文献[11-12]得到了一些精确能控性的结果,而对于有记忆项的退化方程研究很少。文献[10]利用矩方法研究了有记忆项的弱退化抛物方程的近似零能控。 为了研究有记忆的耗散项对弱退化波方程零能控的影响,本文利用文献[11-12]的方法处理记忆项,进而得到有记忆项的弱退化波方程的精确零能控性。
1 预备知识
对任意的α∈[0,1),定义空间
(2)
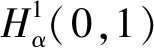
由Hardy-Poincaé不等式[6]
可得:
(3)
其中常数Cα>0。
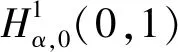
(4)
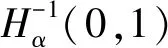
首先,给出精确零能控的定义。
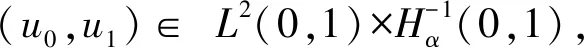
下面给出本文的主要结果:
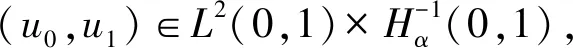
2 解的适定性
由文献[13]的方法给出系统(1)弱解的定义。
定义2若对任意的f∈L1(0,T;L2(0,1))且满足
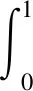
则称函数
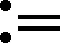
是系统(1)的弱解, 其中y满足如下方程:
(5)
按文献[7]的性质4.2的证明,可得系统(5)有如下性质:
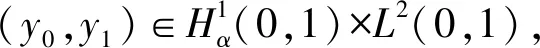
且满足
C‖f‖L1(0,T;L2(0,1))
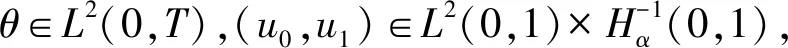
(6)
证明设f∈L1(0,T;L2(0,1)),则由性质1可得
C‖f‖L1(0,T;L2(0,1))
(7)
结合迹定理,可得
(8)
方程(1)两边同乘y,在Q上积分,可得
在空间L1(0,T;L2(0,1))上定义算子
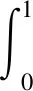
(9)
由Hölder不等式以及式(7)(8),可得
‖θ‖L2(0,T))‖f‖L1(0,T;L2(0,1))
因此,L是空间L1(0,T;L2(0,1))上的有界算子,即存在u∈H满足式(9),则式(6)成立,证明完毕。
3 能观测性不等式
首先,考虑系统(1)的对偶系统:
(10)
为了计算方便,设φ(x,t)=ψ(x,T-t),则
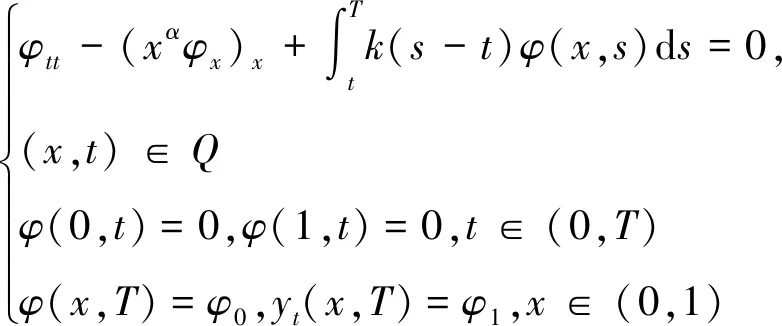
(11)
设
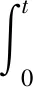
be-a(t-s)(a,b>0)
则ηt(t)=bφ(t)-aη(t),故系统(11)可写为:
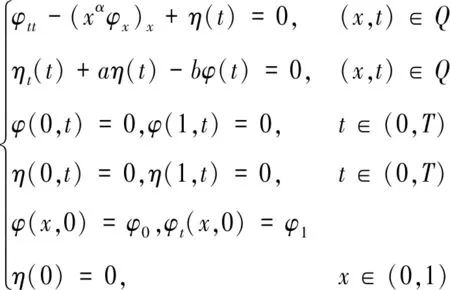
(12)
定义系统(12)的能量如下:
(13)
由η(0)=0可知:
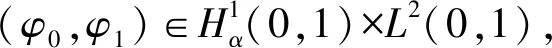
exp(-δt)E(0)≤E(t)≤exp(δt)E(0)
(14)
证明因为
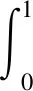
由(3)和Young不等式,可得
(15)
(16)
则
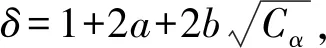
-δE(t)≤E′(t)≤δE(t)
(17)
从0到t积分式(17),可得式(14)成立,证明完毕。
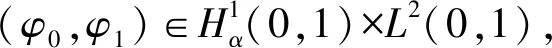
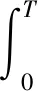
(18)
证明由式(12)两边同乘xφx,在Q上积分,可得
(19)
利用Young不等式有
(20)
其中常数ε,Cε>0。结合引理1估计等式(19),可得式(14)成立,证明完毕。
注记1事实上,式(18)表明φx(1,·)∈L2(0,T)。
下面证明系统(12)的能观测性不等式。
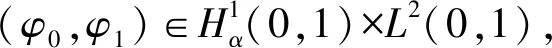
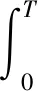
(21)
证明由式(15)两边同乘η,在Q上积分,可得
(22)
将式(19)和(22)相加,有
(23)
结合式(13)(23)可写为
(24)
由式(15)(20)以及引理1可得
取足够小的a、b、ε,使得
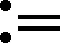
则
(25)
其中0<γ<(2-μ)(1-exp(-δT))/δ。
将不等式(14)的左边在(0,T)上积分,可得
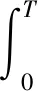
(26)
由式(25)和(26)有
((2-μ)(1-exp(-δT))/δ-γ)E(0)≤
4 精确零能控性
下面证明系统(1)是精确零能控的。
定理1的证明
考虑如下系统:
(27)
式(27)乘以φ,在Q上积分, 其中φ满足系统(11),可得
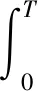
(28)
因此,可以选择θ(t)=φx(1,t)。
定义映射
即Λ(φ0,φ1)=(u1,-u0),则式(28)可以写为