翟兆睿，苏守宝

(1.江苏科技大学 计算机学院, 江苏 镇江 212003；2.金陵科技学院 数据科学与智慧软件江苏省重点实验室, 南京 211169)

粒子群优化(particle swarm optimization,PSO)算法最早由Kennedy和Eberhart提出，是一种群体智能随机优化算法[1-4]。算法源于对鸟群觅食行为的研究和模拟，并将社会学中的合作与竞争引入到优化问题的求解中。由于PSO算法具有结构简单、易于编程实现、有较强的全局优化能力等优点，使其迅速发展成为群体智能方向中最活跃的研究课题之一，成为工程实际中全局优化和复杂问题求解的重要工具。目前，研究者采用多学科方法，对PSO算法理论、模型改进、参数设置、实验设计、混合方法及应用等方面做了一定的创新性研究[5-6]，提出了包括量子粒子群等多种改进型PSO算法，并广泛应用于路径规划、移动隐私保护、大规模协同进化、大数据挖掘等多个研究领域[7-9]。Solteiro Pires等[9]利用分数阶微积分的概念来控制粒子群中粒子的速度变化，从而提出基于分数阶速度粒子群(FV-PSO)算法；同时利用分数阶微积分的概念来控制粒子群中粒子的位置状态，从而提出基于分数阶位置粒子群(FP-PSO)算法，利用粒子的位置和速度信息动态调整分数阶次，逐步形成分数阶粒子群优化方法(FoPSO)[10-12]。最近，分数阶粒子群优化得到了更多国内外学者的进一步关注和研究[13-16]，他们陆续提出改进型或混合型分数阶POS算法[17]，如Micael等[12]引入Darwin分数阶次，提出了一种自适应的分数阶达尔文粒子群优化(AFO-DPSO)算法，并将其成功应用于图像分割、Kalman滤波等领域。

为了克服粒子群优化算法在复杂多峰问题中容易陷入早熟收敛和局部最优、收敛精度不高等问题，已有学者从不同角度对算法进行了改进，以有效缓解全局寻优和局部搜索之间的矛盾。文献[18]提出一种惯性权重线性递减的粒子群(linearly decreasing weight,LDIW-PSO)算法，Clerc和Kennedy等[19]在假设全局最优、个体最优及加速度和惯性权重保持不变的前提下，引入压缩因子，有效地改善了算法鲁棒性。由于分数阶粒子群(FoPSO)算法依赖于分数阶次a线性递减的策略，使算法在全局寻优能力方面性能大幅降低，导致易陷入局部最优。受Clere启发，本文提出了一种动态自适应压缩因子的分数阶粒子群优化算法，分析了压缩因子不动定形式，通过迭代步动态控制压缩因子的变化，以解决FV-PSO算法在后期难以跳出局部搜索能力最优的缺点。

1 分数阶粒子群FPSO算法

1.1 标准粒子群算法

PSO算法源于对鸟类捕食行为的研究。当鸟类捕食时，寻找食物最有效的范围是寻找距离食物最近的鸟的周围区域。假设在一个D维的空间中有m个粒子，其中第i个粒子的位置表示为Xi=(xi1,xi2,…,xiD)，速度表示为Vi=(vi1,vi2,…,viD)，每个粒子根据当前种群中最好粒子在解空间内进行搜索。同时，在每次迭代过程中，粒子通过跟踪2个“极值”来更新自己：第1个是根据粒子本身得到的最优解，即个体极值，用坐标p表示，记为pi=(pi1,pi2,…,piD)；另一个极值是根据整个种群目前得到的最优解，即群体极值，用坐标g表示，记为pg=(pg1,pg2,…,pgD)。粒子也会随个体最优位置和群体最优位置不断更新，当终止条件达到最大迭代次数或满足精度要求其一即可停止，并根据以下公式来更新自己的速度和位置：

vid(t+1)=w×vid(t)+c1×

r1×(pid(t)-xid(t))+

c2×r2×(pgd(t)-xgd(t))

(1)

xid(t+1)=xid(t)+vid(t)

(2)

其中：c1r1(pid(t)-xid(t)) 为自我认知项，具有使粒子具有全局搜索的能力；c2r2(pgd(t)-xid(t))为社会认知项，表示粒子在搜索空间中在寻找最优位置时的趋势；vid(t)是粒子i在第i次迭代中第j维的速度；xid(t)是当前粒子的位置；r1、r2是(0,1)之间的随机数；c1、c2是学习因子；w是惯性权重，表示粒子对自身速度的保留程度。文献[4]指出，在进化过程中，将w初始化为0.9之后会以线性规律降低到0.4，允许在迭代跟随时进行局部搜索的初始探索，并按式(3)线性递减，可称为惯性权重递减PSO算法，即LDIW-PSO。

(3)

其中：t为当前的迭代次数；tmax为迭代总次数。

1.2 分数阶粒子群算法

分数阶微积分的概念可以追溯到差异理论的开始，随着学者对其理论概念研究的成熟，分数阶微积分的研究也开始逐渐被应用在生物学、工业控制和物理等领域[16-17]。

分数阶微积分作为数学分析领域的一个分支，其定义可以被扩展到实数或者多个微分和积分算子，可以用几种分数导数来定义，其中， Grünwald-Letnikov定义的分数导数公式可定义为：

(4)

分数导数相比整数导数需要无限数量的序列，可以在离散时间内实现其近似值，如式(5)所示：

(5)

其中：T是采样周期；r是截断阶数。分数阶模型由于其固有的记忆特性，更加适合描述诸多不可逆性和混沌之类的现象。

利用分数阶a的记忆特性，并通过其递减规律对粒子速度进行更新。起初，为修改速度导数的顺序，原始速度排列方式由式(6)通过左右变换为式(7)：

vt+1=vt+φ1(b-x)+φ2(g-x)

(6)

vt+1-vt=φ1(b-x)+φ2(g-x)

(7)

其中vt+1-vt是分数阶次a=1时离散状态的导数，并假定采样周期T=1以及惯性权重w=1，通过文献[14]的方法得到如式(8)所示的表达式。

Dα[vt+1]=φ1(b-x)+φ2(g-x)

(8)

随着迭代次数的增加，当代粒子群中粒子与最初几代粒子的关系逐渐淡化，并考虑到式(5)给出的r=4的微分导数项，即只保留前4代的速度向量，并取T=1，得到式(9)。

(9)

通过式(8)(9)，得到最终分数阶粒子群算法的速度更新表公式，如式(10)所示[18-19]。

vt+1=αvt+φ1(b-x)+φ2(g-x)+

(10)

2 动态压缩因子的分数阶粒子群优化

2.1 动态压缩因子

借鉴Clerc和Kennedy提出的压缩因子的概念，为了有效地控制和约束粒子的飞行速度，使算法在全局探索和局部搜索两者之间达到平衡，本文给出了一种融合c1、c2值的方法，使用χ来收缩速度，并通过式(11)(12)进行速度更新。

vt+1=χ(vt+φ1β1(b-x)+φ2β2(g-x))

(11)

(12)

其中：χ为压缩因子；φ=c1+c2，φ>4。

在带压缩因子的粒子群算法中，压缩因子的大小直接影响算法的收敛性能，但压缩因子依赖于加速常数c1和c2的大小，当取值过大时，算法具有全局收敛性，可能会将一些空间忽略掉；而当取值过小时，算法容易收敛，存在易陷入局部最优的风险。本文在迭代过程中，通过每次迭代步的变化控制压缩因子的大小，提出了动态压缩因子的方法，如式(13)所示。

(13)

其中：κ为大于1的正整数；tmax为最大迭代次数；t为当前迭代次数；χ为压缩因子，一般χ的取值范围为(0,1)，而κ的取值大小直接影响压缩因子的变化。因此，当κ取不同值时，压缩因子χ变化情况如图1所示。为保证算法的收敛性，实验研究常数κ并不显著影响压缩因子的变化，所以在本文实验中将κ设置为3。

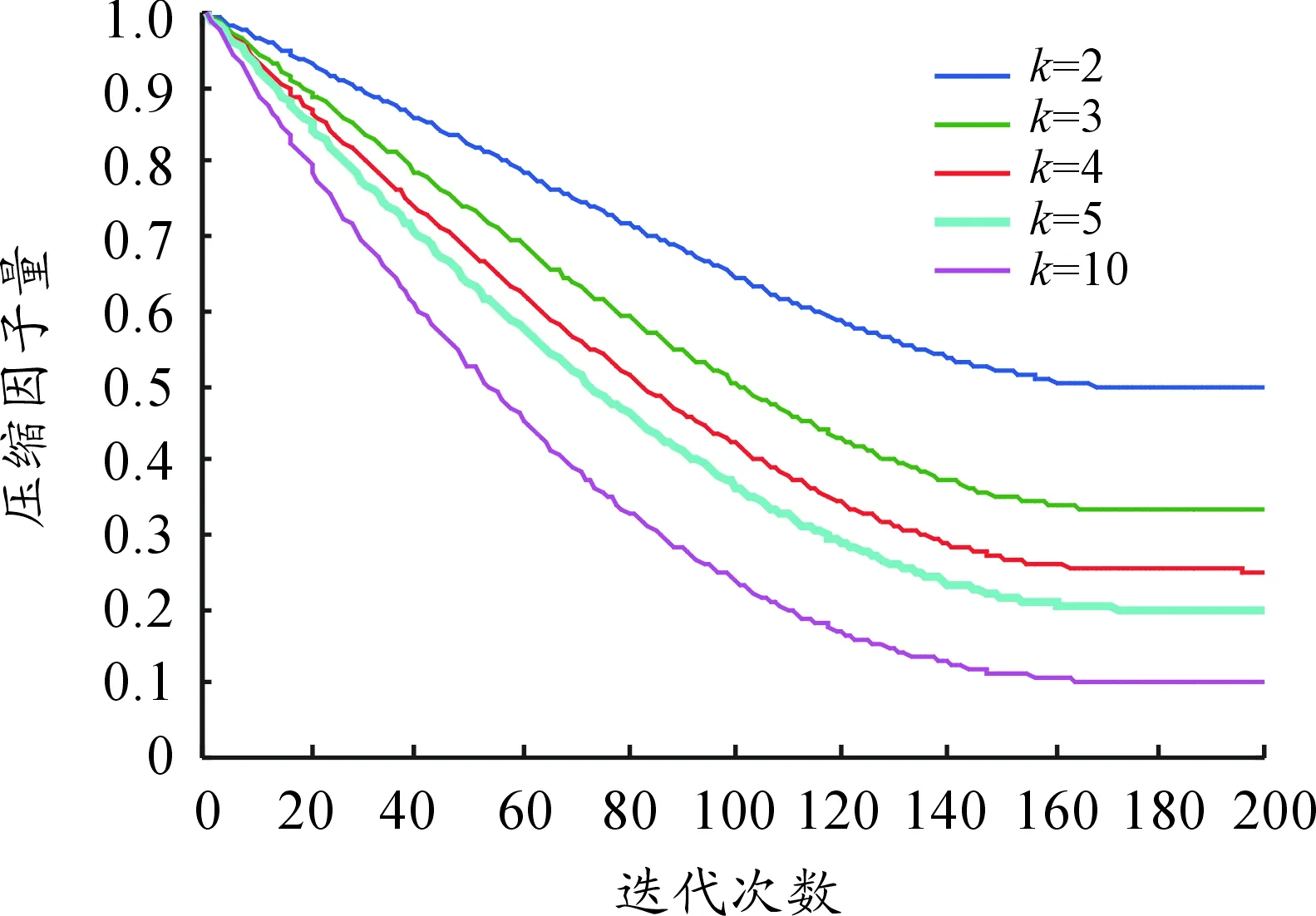
图1 不同κ值时的压缩因子χ变化

2.2 基于动态压缩因子的FoPSO

动态压缩因子的方法改变了原有压缩因子χ值的固定性，可更好地控制粒子的飞行速度，使算法在搜索的早期阶段具有一定的全局寻优能力。随迭代次数的增加，压缩因子逐渐减小，使得算法在搜索后期具有一定的局部搜索能力。为此，本文提出的动态压缩因子的分数阶粒子群(a fractional order PSO with dynamic constriction factor )算法主要过程描述如下：

if (t>Tmax) //条件判断

V=Vmin+(Vmax-Vmin)*rand(1)

//随机初始化种群速度

X=Xmin+(Xmax-Xmin)*rand(1)

//随机初始化种群位置

fort=1:Tmax

forp=1:Mmax

f(t)= fitness_function(y(t));

//计算粒子的适应度值

r1=rand(1);

r2=rand(1);

//生成[0,1]之间随机数

v=range_check(v);

x=range_check(x);

//更新粒子速度、位置及位置范围

end

end

end

其中:Tmax为种群最大迭代次数；Mmax为种群数；fitness_function计算粒子的适应度；range_check更新粒子的速度、位置范围；Vmin和Vmax代表速度范围最小值和最大值；V为粒子的速度向量矩阵；X为粒子位置向量矩阵。

3 实验结果与分析

3.1 测试函数

本文采用的仿真软件为MATLABR2014a，仿真环境：Inter(R) Core(TM)i5-4210H CPU@2.90 GHz 2.90 GHz，内存为4 GB，操作系统为Windows 10。

为了验证本文提出DFFV-PSO算法的性能，笔者选取6个典型的基准函数进行测试，它们是在群智能优化算法中被广泛采用的测试函数(求最小值)，即Sphere、Rosenbrock、Axis parallel hyper-ellipsoid、Rastrigin、Ackley和Griewank函数，表达式分别如下：

1)f1：Sphere函数

(14)

其中-100≤xi≤100,d={1,2,…,D}，全局最优值：min(f1)=f1(0,0,…,D)=0。

2)f2：Rosenbrock函数

(15)

其中-200≤xi≤200,d={1,2,…,D}，全局最优值：min(f2)=f2(0,0,…,D)=0。

3)f3：Axis parallel hyper-ellipsoid函数

(16)

其中-5.12≤xi≤5.12,d={1,2,…,D}，全局最优值：min(f3)=f3(0,0,…,D)=0。

4)f4：Rastrigin函数

(17)

其中-200≤xi≤200,d={1,2,…,D}，全局最优值：min(f4)=f4(0,0,…,D)=0。

5)f5：Ackley函数

(18)

其中-32≤xi≤32,d={1,2,…,D}，全局最优值：min(f5)=f5(0,0,(…,D)=0。

6)f6：Scaffer’sf6函数

(19)

其中-100≤x,y≤100,全局最优值：min(f6)=f6(0,0,)=0。

在这些函数中，f1、f2、f3为单峰函数，该类函数是连续的，在区间上呈现凸状。对于函数f2很难求得全局最优点，而函数f3是对函数f1的变形，增加了各维函数的相互作用。f4、f5、f6为非线性的多峰函数，大量的局部极小值点被认为是很难处理的问题。

3.2 常数k对压缩因子的影响

一般地，k的取值大小直接作用于压缩因子上，从而影响分数阶粒子群算法在函数适应度上的变化。为了实验测试式(13)中常数k对压缩因子χ的影响，本文算法的具体参数设置如下：粒子群群规模设置为30，最大迭代次数设置为200，维度设置如表1所示，学习因子c1=c2=2时，k=2,3,4,5,10。

用本文提出的算法在不同k值时，6个基准函数适应值变化如图2～7所示。从实验结果来看，不同的k值均能保证算法的收敛性，说明常数k并不显著影响压缩因子的变化，所以不失一般性，可在本文实验中将k设置为3，能够保证算法的稳定收敛性能。

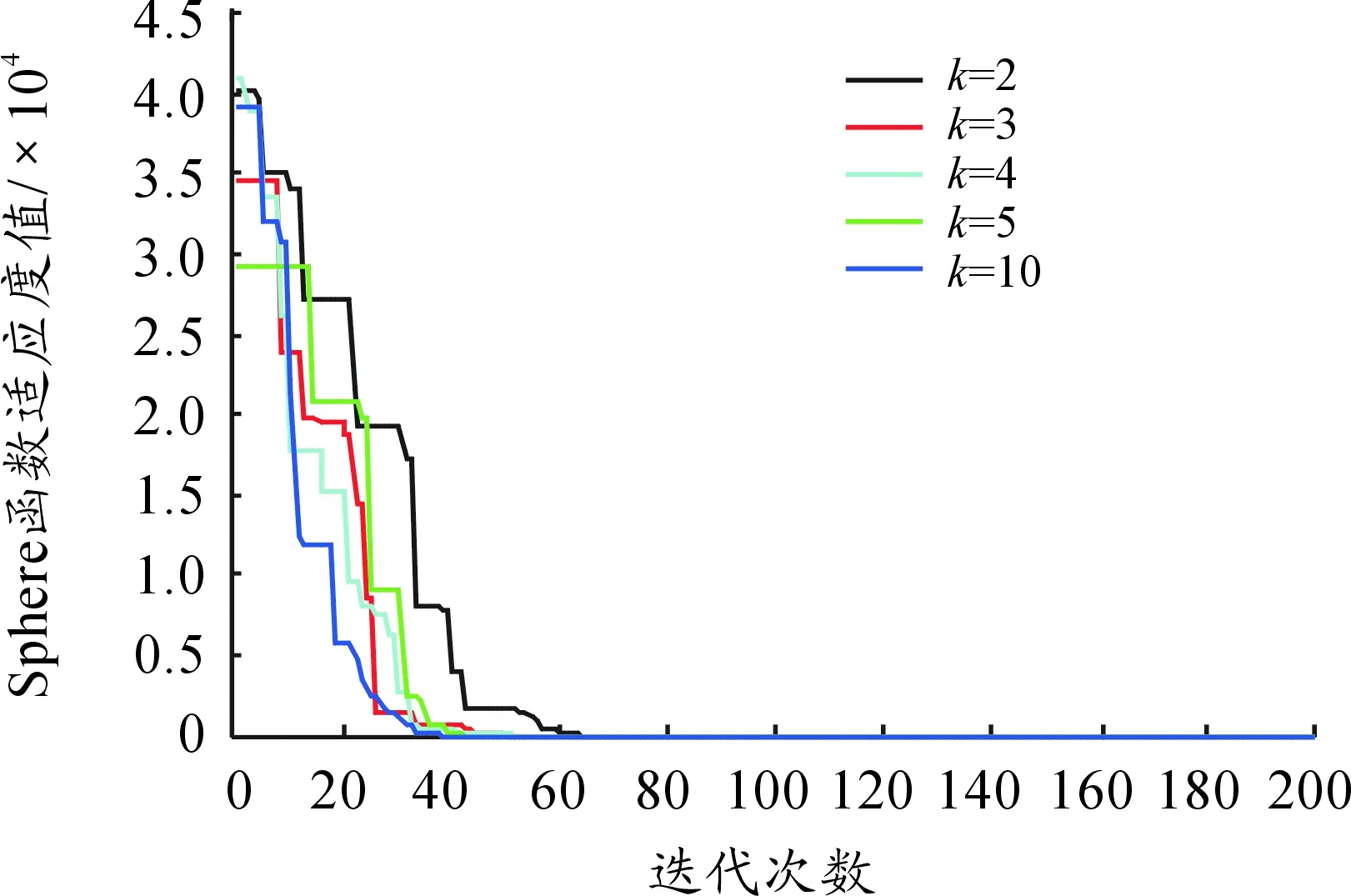
图2 函数Sphere适应度曲线

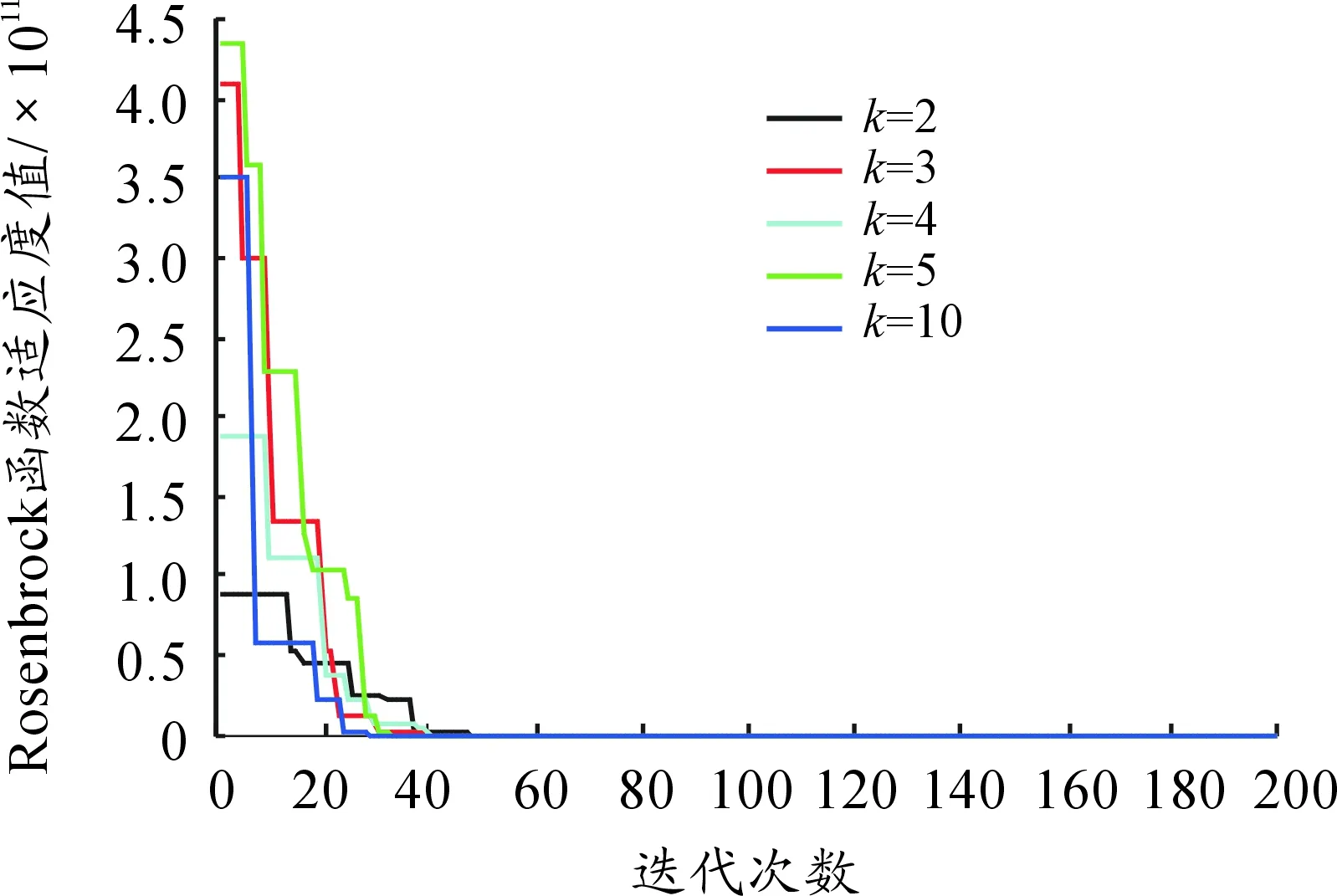
图3 函数Rosenbrock适应度曲线

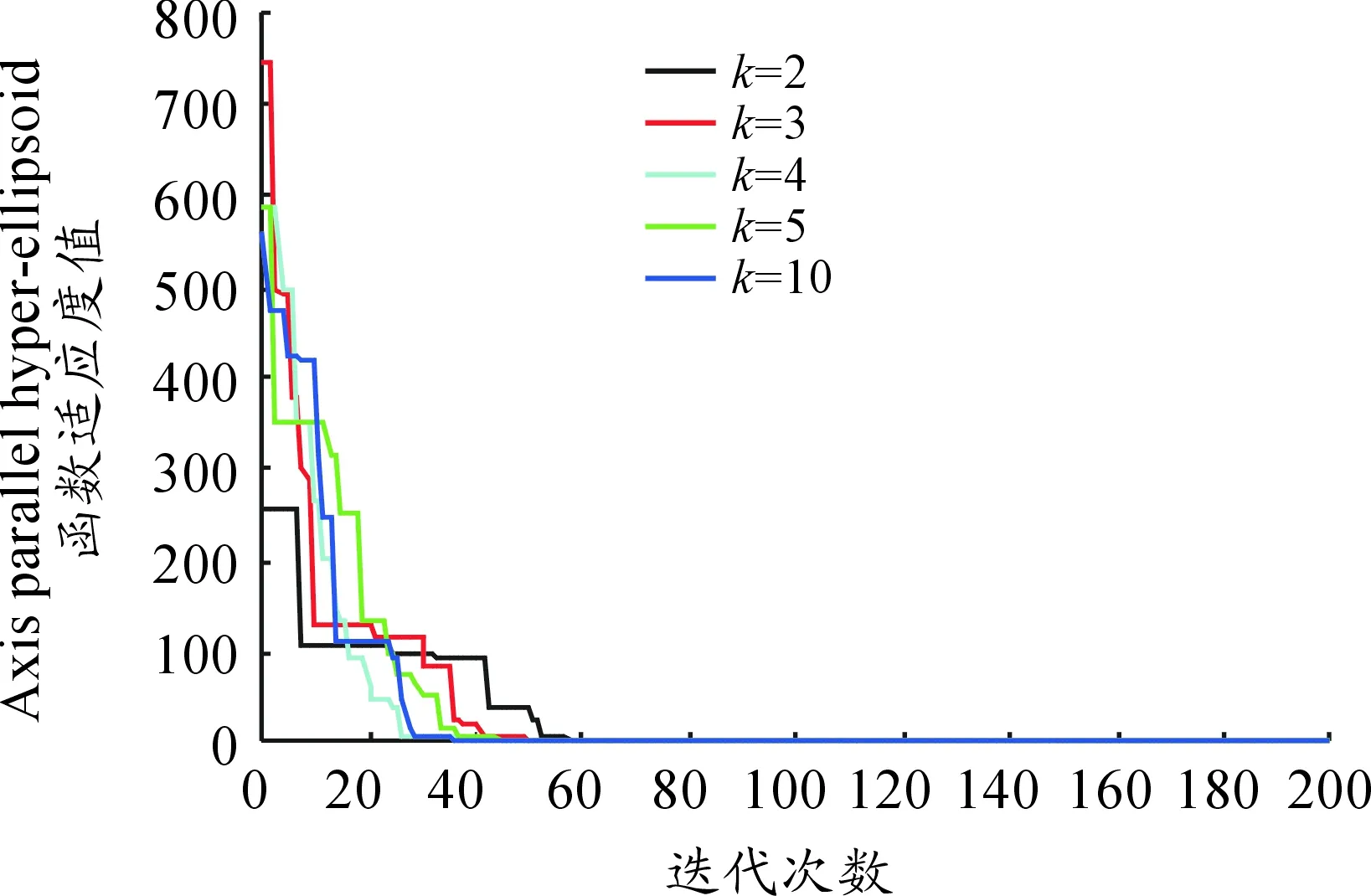
图4 函数Axis parallel hyper-ellipsoidk适应度曲线

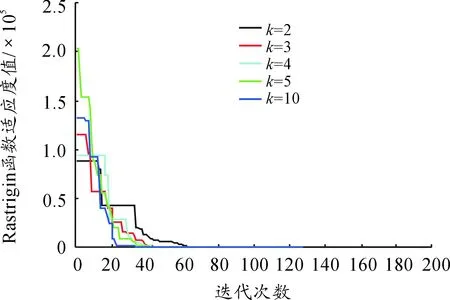
图5 函数Rastrigin适应度曲线

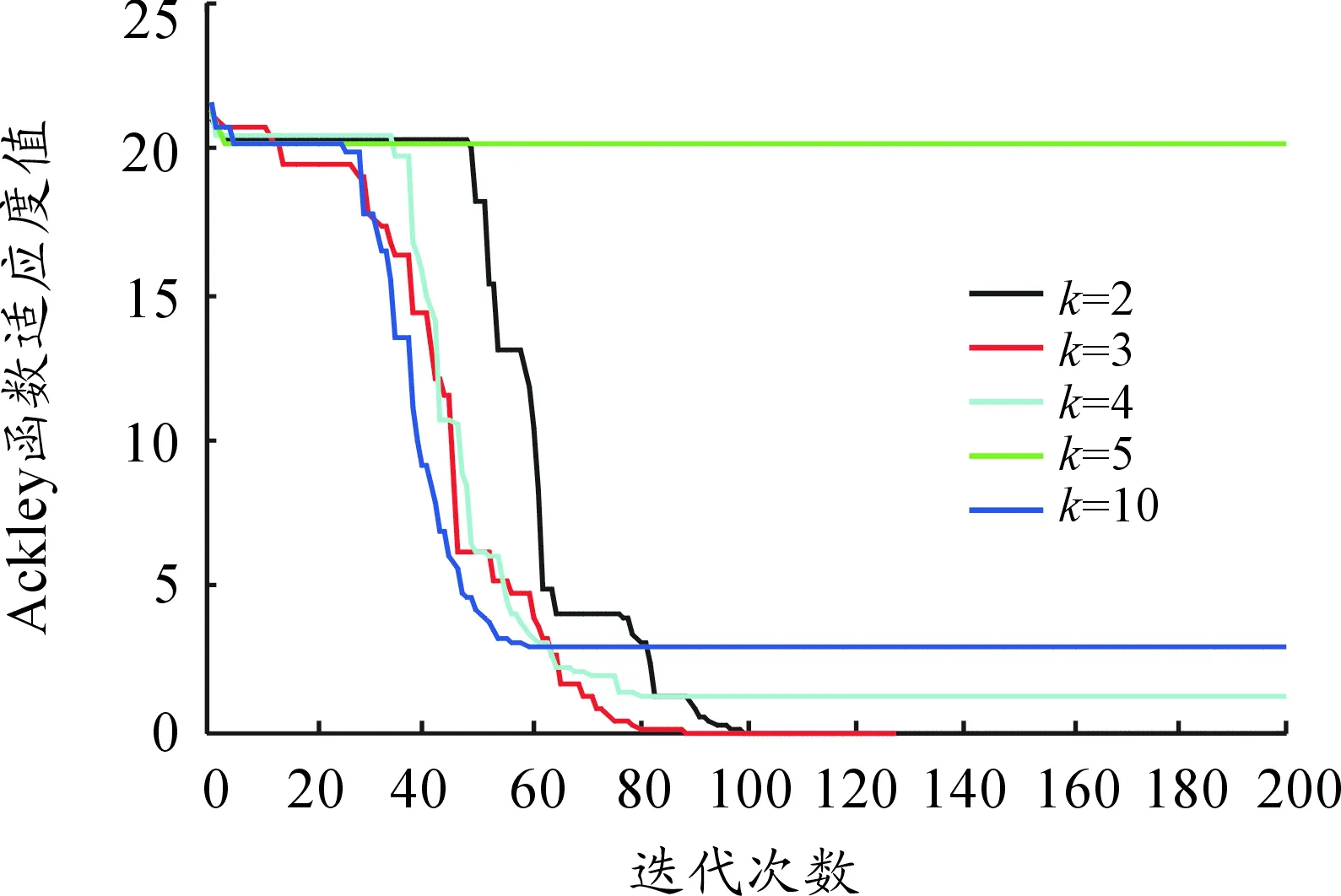
图6 函数Ackley适应度曲线

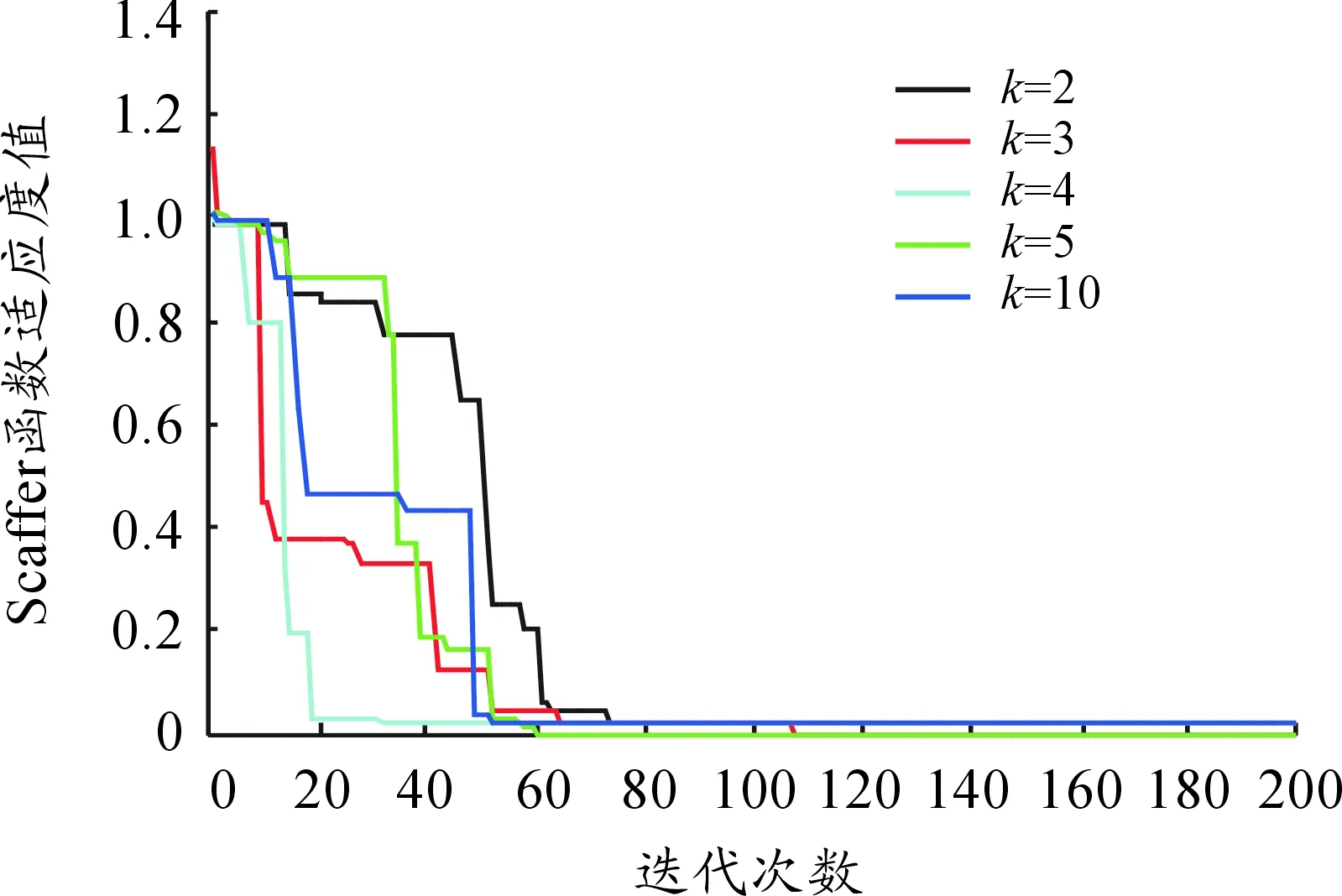
图7 函数Scaffer’s 适应度曲线

3.3 实验结果与分析

在实验中，将提出的DFFV-PSO算法与惯性权重递减粒子群LDIW-PSO算法、分数阶速度粒子群FV-PSO算法、分数阶位置粒子群FP-PSO算法进行比较。参数设置如下：粒子群群规模设置为30，最大迭代次数设置为200，维度设置如表1所示。学习因子c1=c2=2、k=3。为减少统计误差，采用4种不同的算法分别对每个函数独立运行50次，并将50次所得到的结果进行统计，计算算法的适应度值的最优值、最差值和平均值。表1给出了部分实验结果。

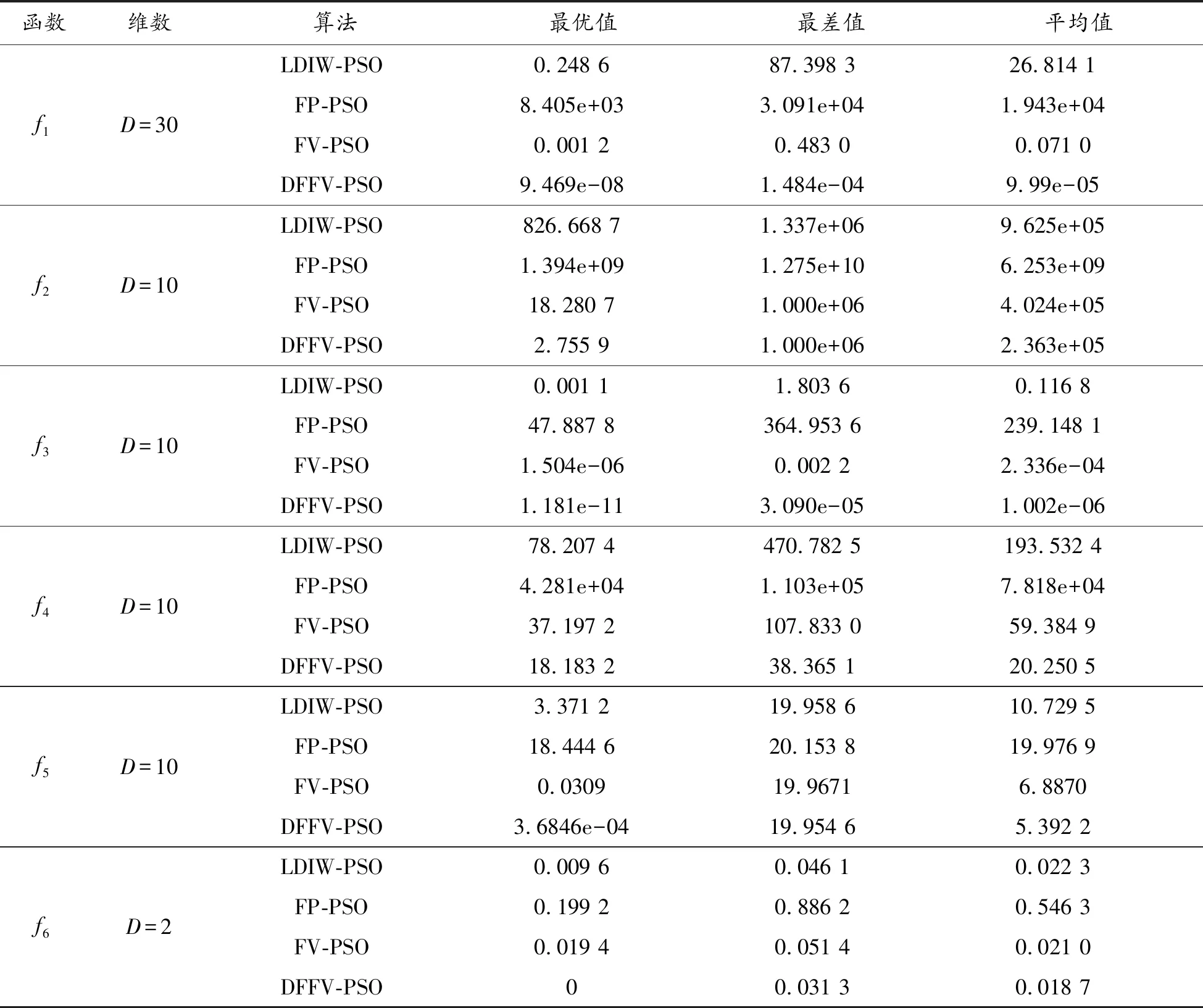
表1 测试函数的部分实验结果

由表1测试结果可以看出，无论是在单峰函数f1、f2、f3上，还是在多峰函数f4、f5、f6上，速度分数阶粒子群算法的测试结果相比其他2种FP-PSO和LDIW-PSO算法都较好，但是在搜索到的最优值的平均值方面均不如本文提出的DFFV-PSO算法性能好。

4种算法对6种函数的优化曲线比较如图8～13所示。

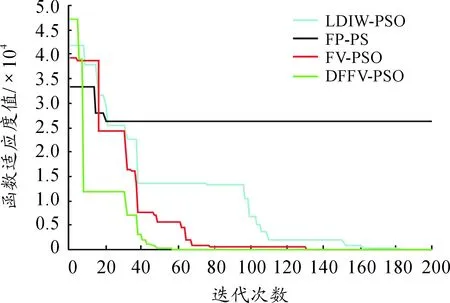
图8 函数Sphere测试结果曲线

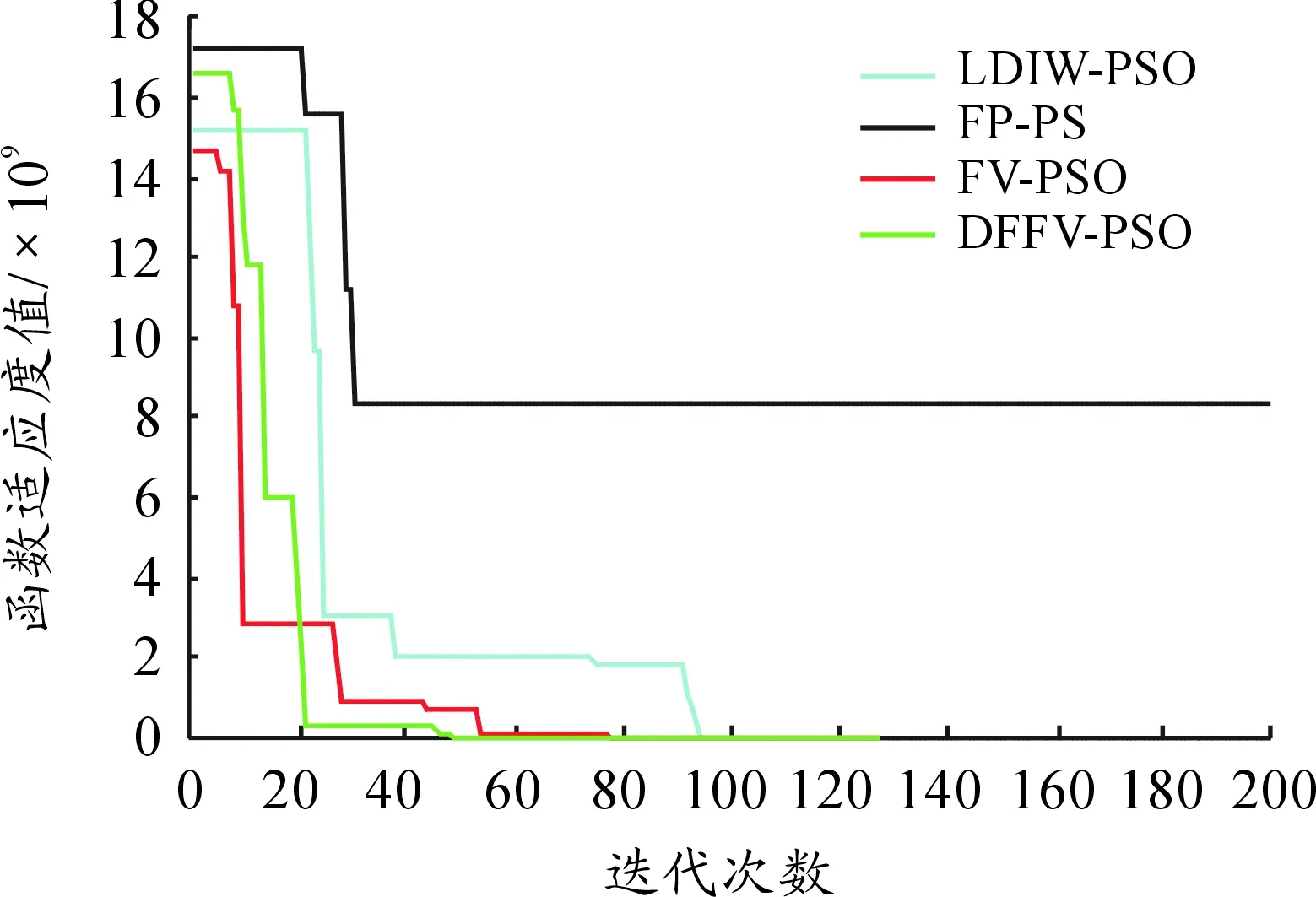
图9 函数Rosenbrock测试结果曲线

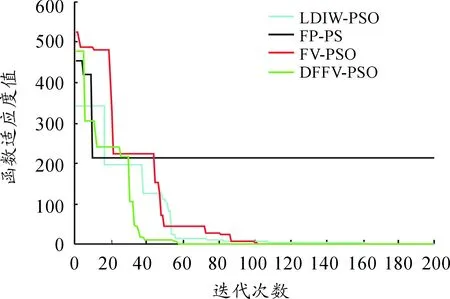
图10 函数Axis parallel hyper-ellipsoid测试结果曲线

观察图8～13可以发现：

1) FV-PSO算法和PSO算法的寻优性能测试结果几乎相差不大。

2) 对于多峰函数，无论是在2维还是在10维下，DFFV-PSO算法的寻优结果均相比其他算法好，鲁棒性更强，收敛速度更快更稳定。

3) 通过将压缩因子的策略融入到算法中，使得改进的DFFV-PSO算法收敛速度更快，寻优能力更强，同时达到优化的精度也最高。

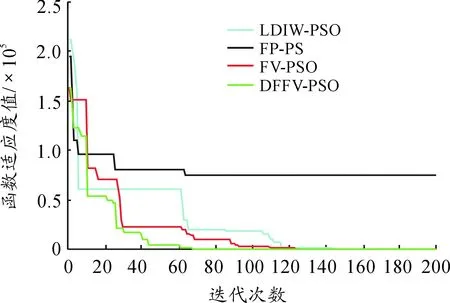
图11 函数Rastrigin测试结果曲线

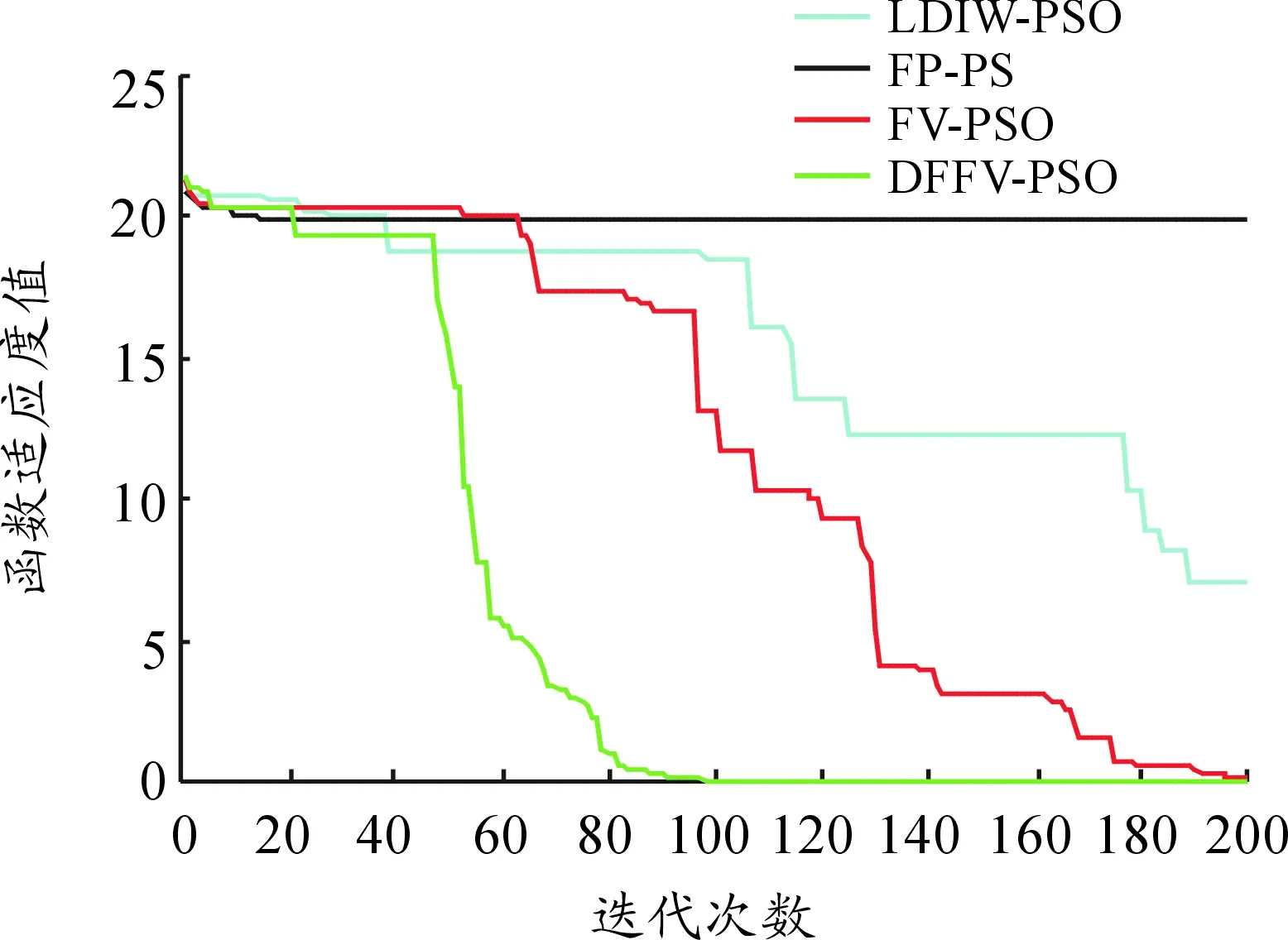
图12 函数Ackley测试结果曲线

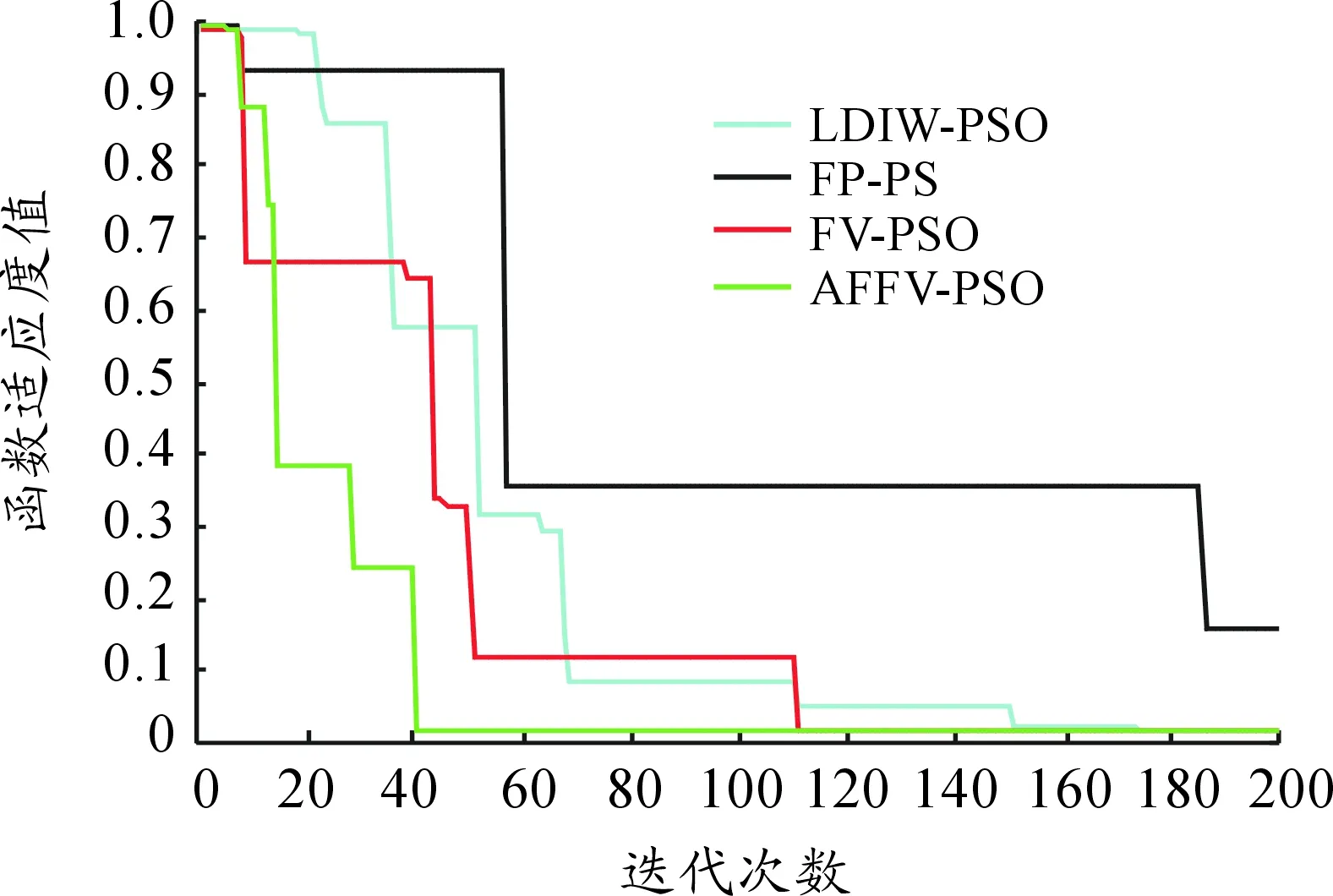
图13 函数Scaffer’s 测试结果曲线

4 结束语

自适应压缩因子的分数阶粒子群算法实际上是在分数阶速度粒子群算法的基础上，结合改变压缩因子的变化，使算法有效地避免了陷入局部最优。实验分析了影响压缩因子的常数k的经验取值，并通过多种基准函数实验仿真结果表明：该算法的收敛速度更快，收敛精度及鲁棒性更好，改进的算法具有可行性和有效性。