一类特殊矩阵的逆特征值问题
2019-07-31段复建
段复建,方 甜,袁 璠
(桂林电子科技大学数学与计算科学学院,广西桂林541004)
1 引言
本文讨论的广义箭形矩阵具有如下形式

其中ai(i=2,···,m+1)互不相同,且bi>0(i=m+1,···,n −1).当m=0 时,具有形式(1.1)的矩阵A 为Jacobi 矩阵,而当m=n −1 时,矩阵A 就变成箭形矩阵.Jacobi 矩阵的特征值反问题具有广泛的应用,关于此类问题研究已取得一些比较好的结果,详见文献[1–4].箭形矩阵的特征值反问题在现代控制理论中有着广泛的应用,文献[5,6]分别讨论了对称三对角矩阵和对称爪形矩阵的特征值反问题.对于一些特殊箭形矩阵的特征值反问题的研究见文献[7–9].Gladwell 从力学角度阐述了振动中的一些特征值反问题[10],其中弹簧–质量系统等振动结构参数识别问题,往往归结为Jacobi 矩阵特征值反问题,星形弹簧质量系统的振动问题则转化为箭形矩阵的特征值反问题.
具有形式(1.1)的广义箭形矩阵的特征值反问题在文献[11–13]中有讨论,鉴于上述工作以及此类矩阵的重要性,本文重点研究具有形式(1.1)的广义箭形矩阵的特征值反问题,我们推广了Jacobi 矩阵和箭形矩阵逆特征值问题,提出了两类逆问题,给出了问题有唯一解的充分必要条件,给出了解的表达式及相应数值例子.
本文研究广义箭形矩阵的两类逆问题,即
问题I给出三个非零互异实数λ1,λ2,µ以及三个非零实向量x1=(x1,···,xm+1)T,x2=(xm+1,···,xn)T,y=(y1,···,yn)T.求具有形式(1.1)的n 阶矩阵A 使得(λ1,x1),(λ2,x2),(µ,y)分别是A1,m+1,Am+1,n和A 的特征对.
问题II给出两个非零互异实数λ,µ和两个非零实向量x=(x1,···,xn)T,y=(y1,···,yn)T,求具有形式(1.1)的矩阵A 和A∗,使得(λ,x),(µ,y)分别为矩阵A,A∗的特征对.
矩阵A 的的主子式A1,m+1,Am+1,n和矩阵A∗分别具有如下形式
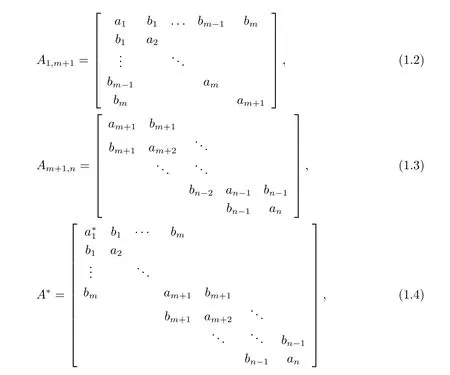
其中ai(i=2,···,m+1)互不相同,且bi>0(i=m+1,···,n −1),可知A1,m+1,Am+1,n分别为箭形矩阵和Jacobi 矩阵.式(1.4)中除元素a∗1与a1不同外,其它元素与(1.1)式矩阵A 中元素相同.
现在作如下约定
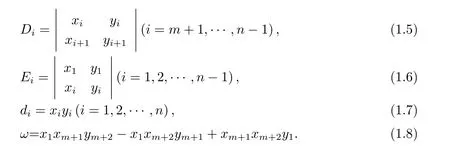
2 主要结果
下面给出本文将要用到的必要引理.
引理2.1[14]设λ 为n 阶Jacobi 矩阵J 的特征值,x=(x1,x2,···,xn)T为J 对应于λ的特征向量,则
(2)x 的相邻的两个分量不同时为零;
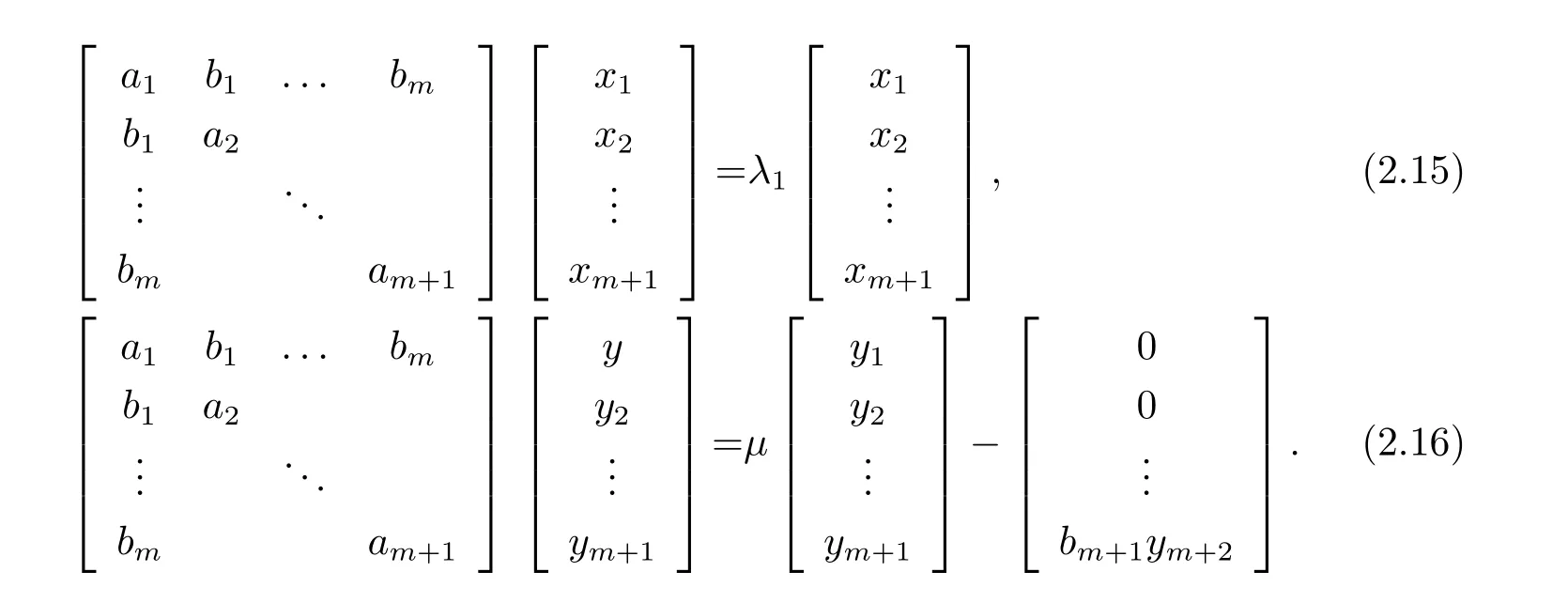
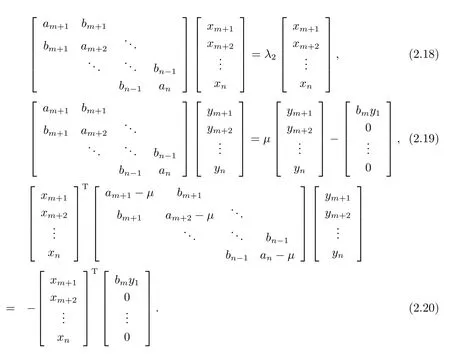
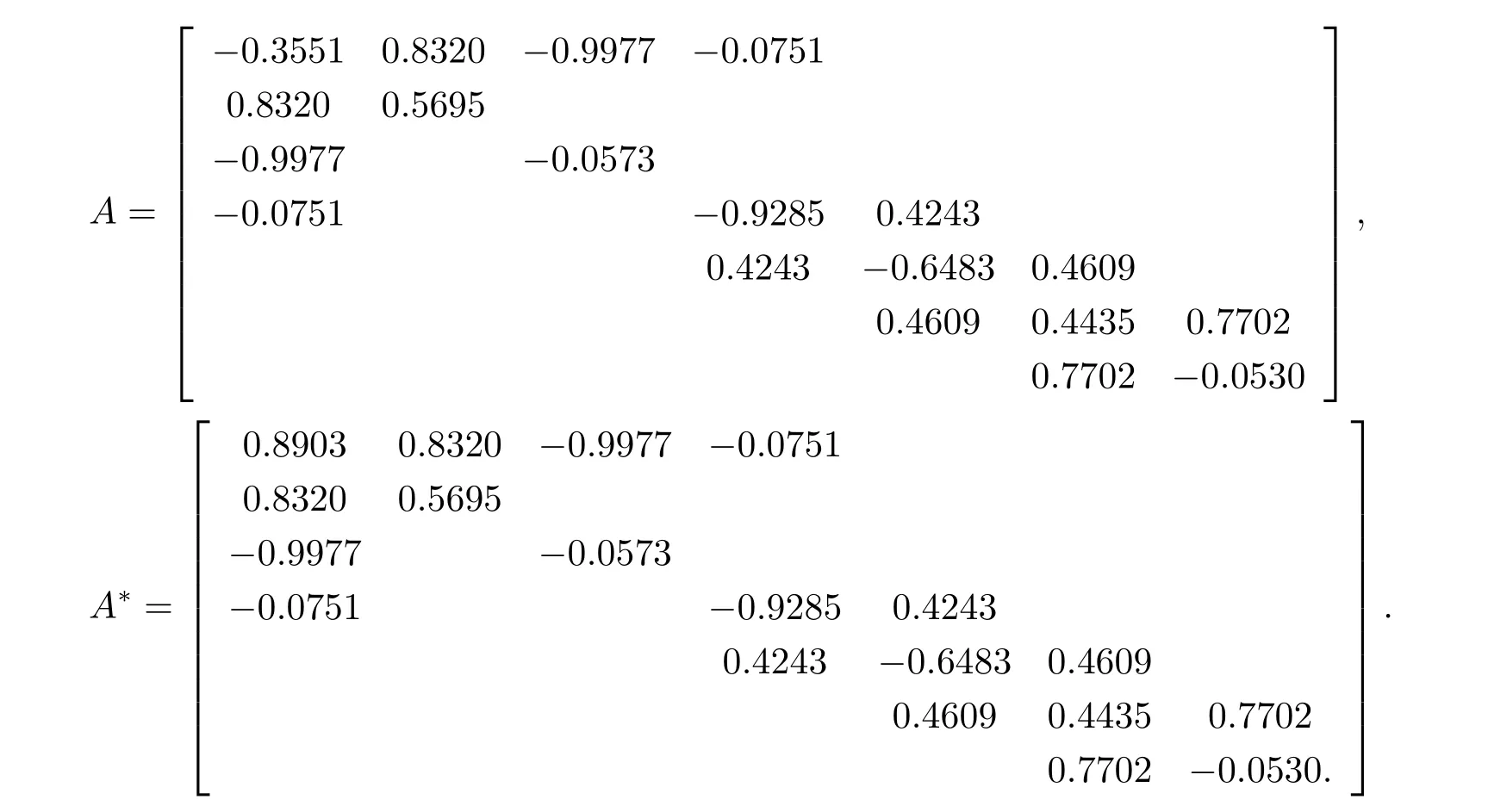
(3)若某个i(1 对于问题I 给出定理2.1. 定理2.1问题I 有唯一解的充分必要条件为 (i)xi(i=m+1,···,n)满足引理2.1 的条件; 且当问题有解时,解由下式给出 证 充分性因(λ1,x1),(µ,y)分别是A1,m+1,A 特征对,有A1,m+1x1=λ1x1,Ay=µy. (1)当2 ≤i ≤m 时,有如下线性方程组 由上式消去ai,即bi−1Ei=(λ −µ)di.由条件(ii)(i=2,···,m),则ai,bi有唯一解 下证(2.3)中ai的两个表达式等价,由(2.2)式知 所以(2.3)式中ai的两个表达式等价得证. (2)当i=m+1 时,由A1,m+1x1=λ1x1,Ay=µy,Am+1,nx2=λ2x2得下线性方程组 (3)当i=1 时,由A1,m+1x1=λ1x1,Ay1=µy1,得 则有 将bi(i=1,···,m)的表达式带入a1,利用条件(iii)可证得a1的两个表达式都存在则相等. 下证上述表达式相等.由条件(iii)有 则有 则可推出 在(2.8)式两边同时除以x1y1,得证a1的两个表达式相等. (4)当m+2 ≤i ≤n−1 时,由Am+1,nx2=λ2x2,Ay=µy,得 由上式消去ai得 即为biDi=bi−1Di−1−(λ2−µ)di.递推可得 下证式(2.12)中ai的两个表达式等价,由(2.11),(2.12)式知 所以(2.12)式中ai的两个表达式等价得证. (5)当i=n 时,可得an的表达式如下 根据(2.11)式,利用条件(iii),可证得an的两个表达式都存在则相等. 根据条件(i)和(iv)可知所求ai,bi满足问题I 要求,问题I 有唯一解,充分性得证,且给出解的表达式(2.2),(2.3),(2.5),(2.7),(2.11),(2.12),(2.14). 必要性若问题I 有唯一解,则上述线性方程组(2.1),(2.4),(2.6),(2.9)有唯一解,则可以推条件(ii)成立,又因为矩阵An的顺序主子式Am+1,n为Jacobi 矩阵,若问题I 有解,则条件(i)和(iv)成立.下证条件(iii)成立. 若问题I 有解则要满足A1,m+1x1=λ1x1,Ay=µy,则有 在(2.15)式两边同时左乘x1得 下面讨论问题II,给出定理2.2. 定理2.2问题II 有唯一解的充分必要条件为 且当问题有解时,解由下式给出 证必要性由于(λ,x),(µ,y)分别为A,A∗的特征对,所以有 则上式可表示为 问题II 的解等价于求解上述线性方程组 由式(2.25)消去an,由条件(i)知bn−1,an有唯一解,所以有 利用(2.26)式易证明(2.27)式中an的两个表达式等价. 通过递推得 结合式(2.21),则bi的表达式为 利用(2.28)式易证(2.29)式中ai+1的两个表达式等价. 利用(2.30)式可证(2.31)式中am+1的两个表达式等价. 充分性得证,且给出问题II 解的表达式(2.27)–(2.35). 必要性若问题II 有唯一解,则上述线性方程组(2.21)–(2.25)有唯一解,则可以推得条件(i)成立.若问题II 有解,根据矩阵A,A∗的特殊性以及bi(i=m+1,···,n −1)的表达式,则条件(ii)成立. 步骤1验算所给λ1,λ2,µ以及三个非零实向量 是否满足定理2.1 的条件(i)–(iv).是,则进行下一步;否则,停止. 步骤2根据定理2.1 中的公式(2.2),(2.3),(2.5),(2.7),(2.11),(2.12),(2.14),求解ai,bi,形成广义箭形矩阵A. 例1给实数λ1=1.0879,λ2=0.5689,µ=0.9730,m=3,n=7 给定实向量x1,x2,y 如下x1=(−0.5667,0.0961,−0.3903,0.7193)T,x2=(0.7193,0.1702,−0.4556,−0.2676)T,y=(0.4109,−0.0752,0.3080,−0.4426,0.1225,0.6568,0.2972)T. 根据算法1 中的步骤将λ1,λ2,µ,x1,x2,y 带入定理2.1 的条件(i)–(iv),验算可知所给数据满足有唯一解的条件,利用公式(2.2),(2.3),(2.5),(2.7),(2.11),(2.12),(2.14)通过MATLAB 编程计算ai,bi,形成广义箭形矩阵A,得到A 如下 容易验证(λ1,x1)是A1,6的一个特征对,(λ2,x2)是A5,10的一个特征对,(µ,y)是A 的一个特征对,所以A 是所要求的矩阵. 步骤1验算所给数据λ,µ和两个非零实向量x=(x1,···,xn)T,y=(y1,···,yn)T是否满足定理2.2 的要求.是,则进行下一步;否则,停止. 步骤2根据定理2.2 中公式(2.27)–(2.35),求解 分别形成广义箭形矩阵A,A∗,使得(λ,x)和(µ,y)分别为矩阵A,A∗的特征对. 例2给定实数λ=−0.5435,µ=−0.0032,m=3,n=7,给定实向量x,y 如下x=(−0.0047,−0.0076,0.0041,−0.0472,−0.2254,−0.8072,−0.5435),y=(−0.2201,0.8056,0.5498,0.0149,0.0056,−0.0016,−0.0032). 根据算法2 中的步骤将λ,µ,x,y 带入定理2.2 中的(i)和(ii),验算可知所给数据满足有唯一解的条件,根据式(2.27)–(2.35),通过Matlab 编程计算得到(i=2,···,n),bi(i=1,···,n −1),并形成广义箭形矩阵A 和A∗,如下所示 易知(λ,x)是矩阵A 的一个特征对,(µ,y)为矩阵A∗的一个特征对,所以A,A∗是所要求的矩阵.
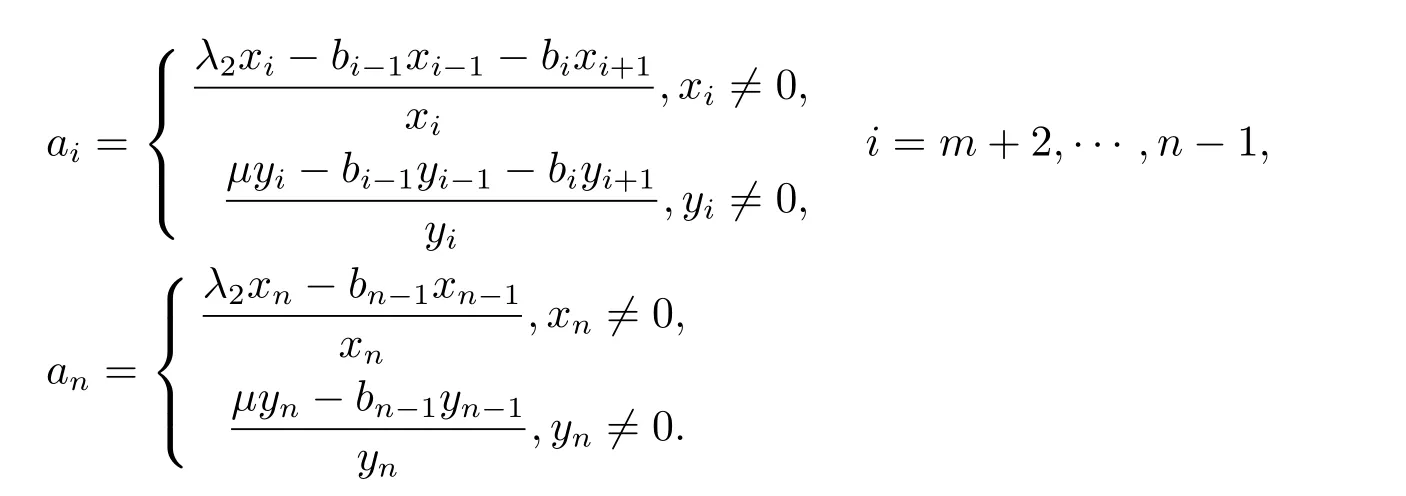


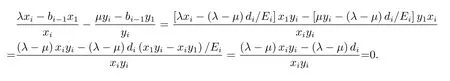


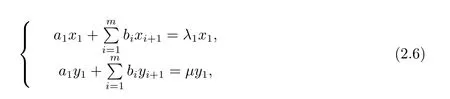

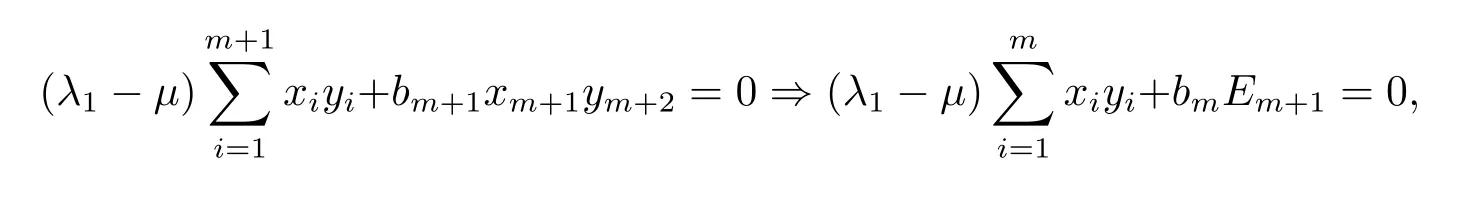
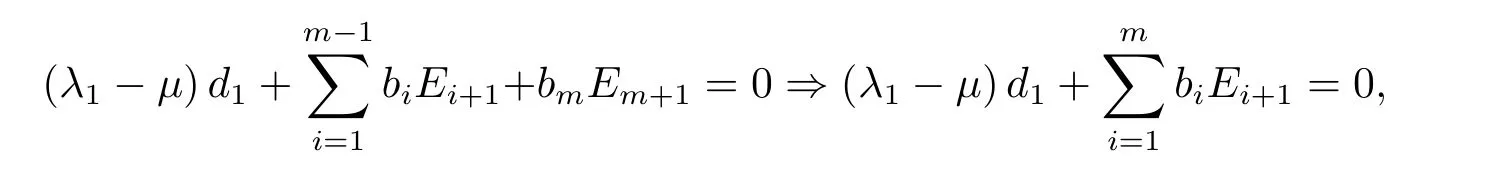
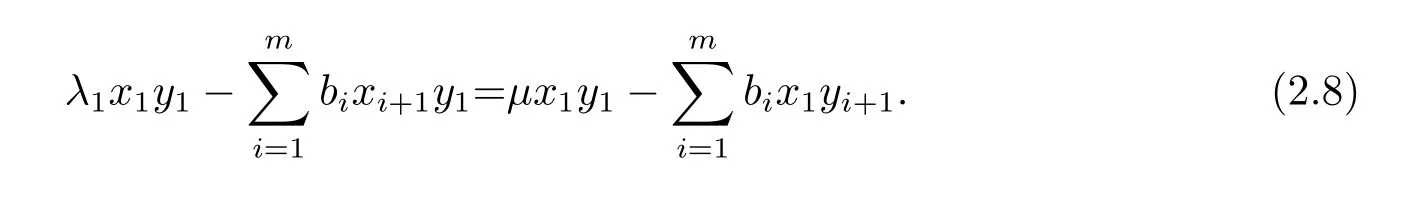
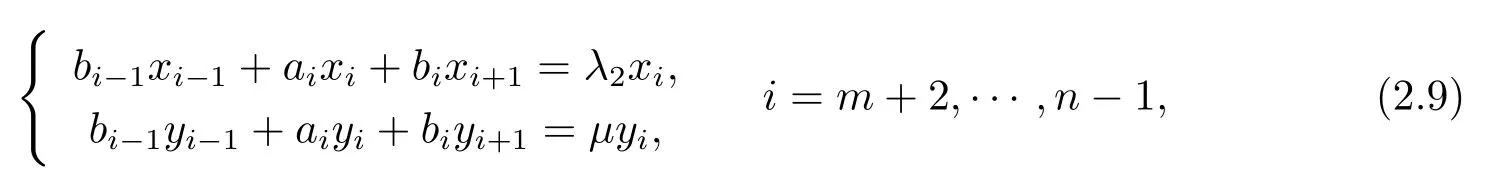
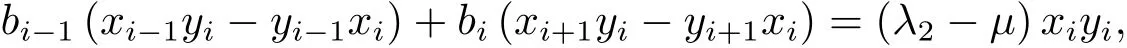
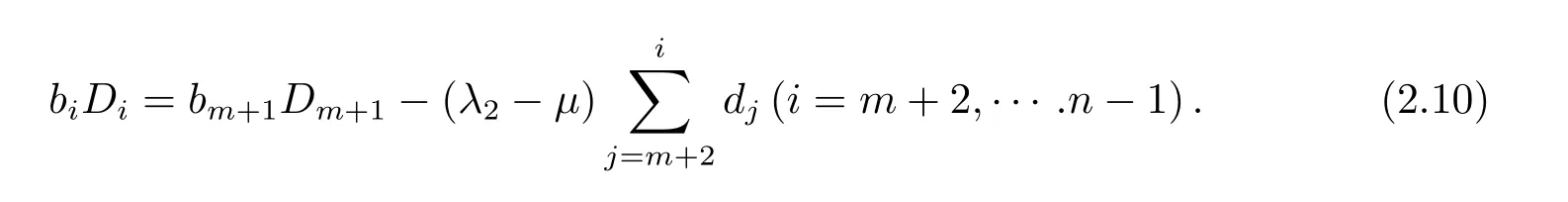
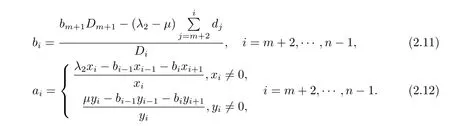
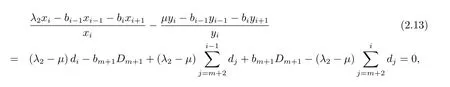







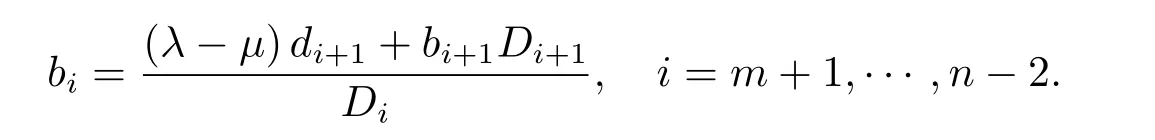
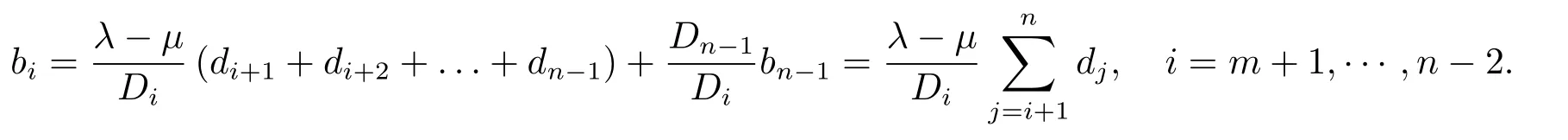
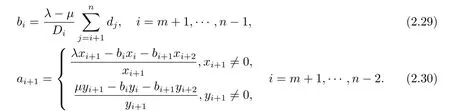
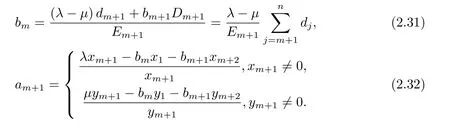
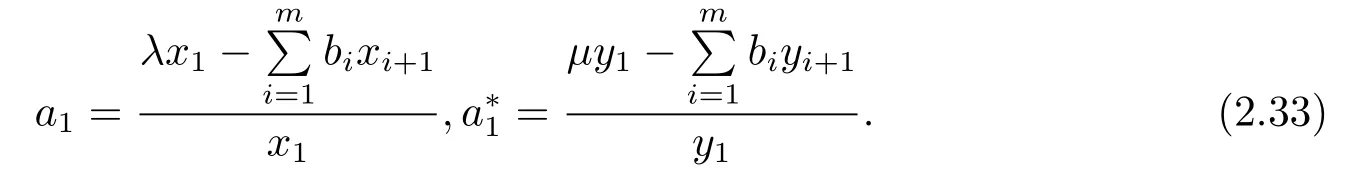
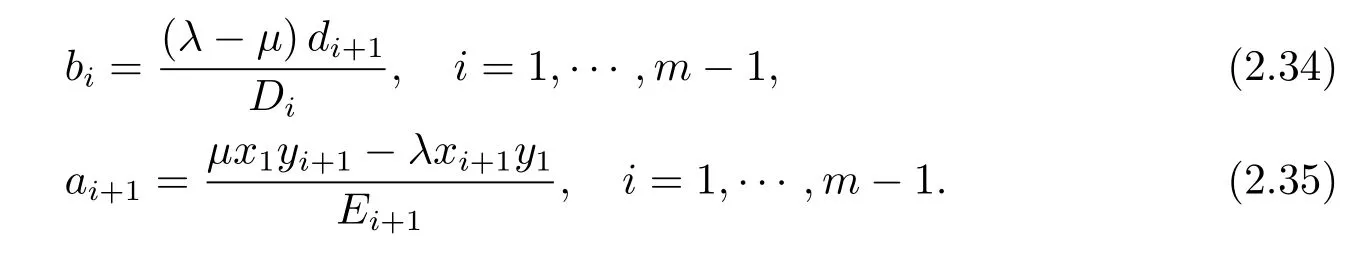
3 算法及数值实验
3.1 算法1
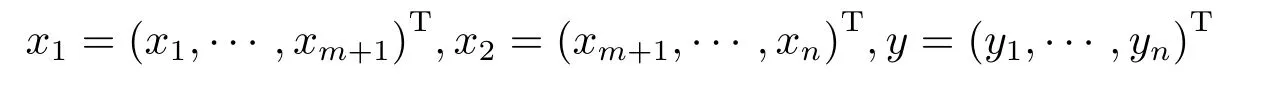

3.2 算法2
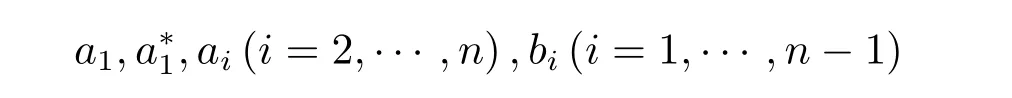
猜你喜欢
杂志排行
数学杂志的其它文章
- ANALYTIC REGULARITY OF SOLUTIONS TO SPATIALLY HOMOGENEOUS LANDAU EQUATION
- GRADUAL HAUSDORFF METRIC AND ITS APPLICATIONS
- EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR CAPUTO-HADAMARD TYPE FRACTIONAL DIFFERENTIAL EQUATIONS
- CONCENTRATION IN THE FLUX APPROXIMATION LIMIT OF RIEMANN SOLUTIONS TO THE EXTENDED CHAPLYGIN GAS EQUATIONS
- ASYMPTOTIC BEHAVIOR OF COMPRESSIBLE NAVIER-STOKES FLUID IN POROUS MEDIUM
- 五次非线性Schrödinger 方程的一个新型守恒紧致差分格式
