CONCENTRATION IN THE FLUX APPROXIMATION LIMIT OF RIEMANN SOLUTIONS TO THE EXTENDED CHAPLYGIN GAS EQUATIONS
2019-07-31ZHANGQingling
ZHANG Qing-ling
(School of Mathematics and Computer Sciences,Jianghan University,Wuhan 430056,China)
Abstract:In this paper,two kinds of occurrence mechanism on the phenomenon of concentration and the formation of delta shock waves in the flux approximation limit of Riemann solutions to the extended Chaplygin gas equations are analyzed. By phase plane analysis and generalized characteristic analysis,we construct the Riemann solution to the extended Chaplygin gas equations completely and obtain two results:on one hand,as the pressure vanishes,any two-shock Riemann solution to the extended Chaplygin gas equations tends to a δ-shock solution to the transportation equation;on the other hand,as the pressure approaches the generalized Chaplygin pressure,any two-shock Riemann solution tends to a δ-shock solution to the generalized Chaplygin gas equations,which generalize to the extended Chaplygin gas.
Keywords: extended Chaplygin gas;δ-shock wave;flux approximation limit;Riemann solutions;transportation equations;generalized Chaplygin gas
1 Introduction
The extended Chaplygin gas equations can be expressed as
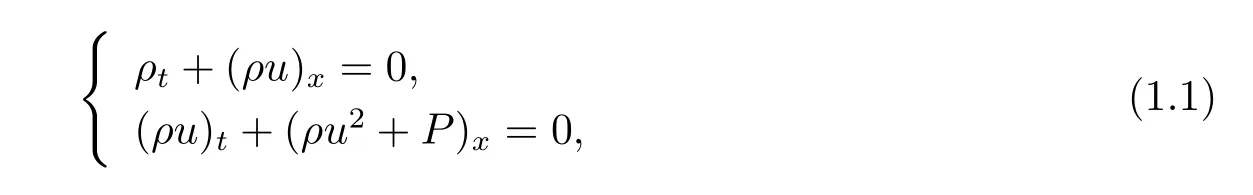
where ρ,u and P represent the density,the velocity and the scalar pressure,respectively,and
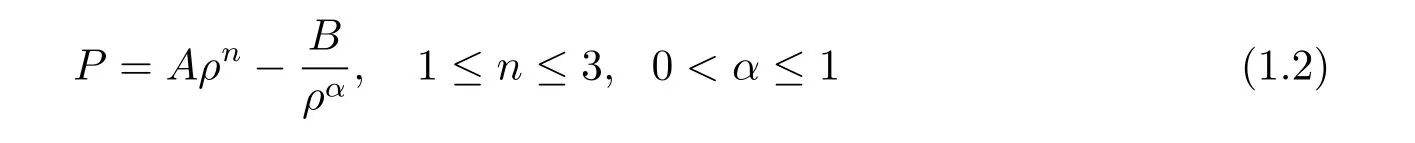
with two parameters A,B>0.
This model was proposed by Naji[1]to study the evolution of dark energy.For n=2,this model can also be seen as the magnetogasdynamics with generalized Chaplygin pressure[2]. When B=0 in(1.2),P=Aρnis the standard state equation for perfect fluid. Up to now,various kinds of theoretical models have been proposed to interpret the behavior of dark energy. Specially,when n=1 in(1.2),it reduces to the state equation for modified Chaplygin gas,which was originally proposed by Benaoum in 2002[3].As an exotic fluid,such a gas can explain the current accelerated expansion of the universe. Whereas when A=0 in(1.2),P =is called the pressure for the generalized Chaplygin gas[4].Furthermore,when α=1,P=is called the pressure for(pure)Chaplygin gas which was introduced by Chaplygin[5],Tsien[6]and von Karman[7]as a suitable mathematical approximation for calculating the lifting force on a wing of an airplane in aerodynamics.It has also been advertised as a possible model for dark energy[8].
When two parameters A,B →0,the limit system of(1.1)with(1.2)formally becomes the following transportation equations

which is also called the zero-pressure gas dynamics,and can be used to describe some important physical phenomena,such as the motion of free particles sticking together under collision and the formation of large scale structures in the universe[9–11].
The transportation equation(1.3)were studied extensively since 1994.The existence of measure solutions of the Riemann problem was first proved by Bouchut[12]and the existence of the global weak solutions was obtained by Brenier and Grenier[13]and Rykov and Sinai[10].Sheng and Zhang[14]discovered that the δ-shock and vacuum states do occur in the Riemann solutions to the transportation equations(1.3)by the vanishing viscosity method.Huang and Wang[15]proved the uniqueness of the weak solution when the initial data is a Radon measure.Also see[14,16–19]for more related results.
δ-shock is a kind of nonclassical nonlinear waves on which at least one of the state variables becomes a singular measure. Korchinski[20]first introduced the concept of the δ-function into the classical weak solution in his unpublished Ph.D.thesis.Tan,Zhang and Zheng[21]considered some 1-D reduced system and discovered that the form of δ-functions supported on shocks was used as parts in their Riemann solutions for certain initial data.LeFloch et al.[22]applied the approach of nonconservative product to consider nonlinear hyperbolic systems in the nonconservative form. Recently,the weak asymptotic method was widely used to study the δ-shock wave type solution by Danilov and Shelkovich et al.[23–25].
As for delta shock waves,one research focus is to explore the phenomena of concentration and cavitation and the formation of delta shock waves and vacuum states in solutions.In[26],Chen and Liu considered the Euler equations for isentropic fluids,i.e.,in(1.1),they took the prototypical pressure function as follows:

They analyzed and identified the phenomena of concentration and cavitation and the formation of δ-shocks and vacuum states as ε →0,which checked the numerical observation for the 2-D case by Chang,Chen and Yang[27,28].They also pointed out that the occurrence of δ-shocks and vacuum states in the process of vanishing pressure limit can be regarded as a phenomenon of resonance between the two characteristic fields. Moreover,they made a further step to generalize this result to the nonisentropic fluids in[29].Besides,the results were extended to the relativistic Euler equations for polytropic gases in[30],the perturbed Aw-Rascle model in[31],the magnetogasdynamics with generalized Chaplygin pressure in[2],the modified Chaplygin gas equations in[32,33],etc.
In this paper,we focus on the extended Chaplygin gas equations(1.1)to discuss the phenomena of concentration and cavitation and the formation of delta shock waves and vacuum states in Riemann solutions as the double parameter pressure vanishes wholly or partly,which corresponds to a two parameter limit of Riemann solutions in contrast to the previous works in[2,26,29–31]. Equivalently,we study the limit behavior of Riemann solutions to the extended Chaplygin gas equations as the pressure vanishes,or tends to the generalized Chaplygin pressure.
It is noticed that,When A,B →0,system(1.1)with(1.2)formally becomes the transportation equations(1.3).For fixed B,when A →0,system(1.1)with(1.2)formally becomes the generalized Chaplygin gas equations
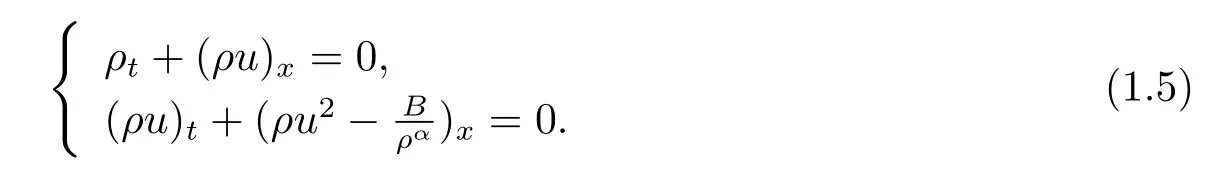
When α=1,it is just the Chaplygin gas equations.In 1998,Brenier[34]first studied the 1-D Riemann problem and obtained the solutions with concentration when initial data belongs to a certain domain in the phase plane.Recently,Guo,Sheng and Zhang[35]abandoned this constrain and constructively obtained the general solutions of the 1-D Riemann problem in which the δ-shock wave developed.Moreover,in that paper,they also systematically studied the 2-D Riemann problem for isentropic Chaplygin gas equations.In[36],Wang solved the Riemann problem of(1.5)by the weak asymptotic method.It has been shown that,in their results,δ-shocks do occur in the Riemann solutions,but vacuum states do not. For more results about Chaplygin gas,one can refer to[37–40].
In this paper,we first solve the Riemann problem of system(1.1)with Riemann initial data
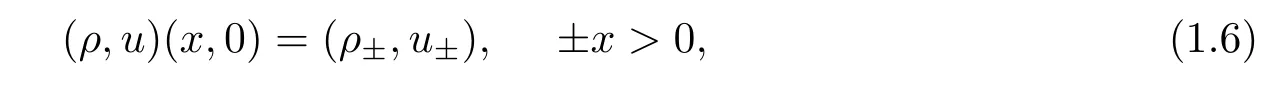
where ρ±>0, u±are arbitrary constants. With the phase plane analysis method,we construct the Riemann solutions with four different structures:R1R2,R1S2,S1R2and S1S2.
Then we analyze the formation of δ-shocks and vacuum states in the Riemann solutions to the extended Chaplygin gas equations as the pressure vanishes. It is shown that,as the pressure vanishes,any two-shock Riemann solution tends to a δ-shock solution to the transportation equations,and the intermediate density between the two shocks tends to a weighted δ-measure that forms the δ-shock;by contrast,any two-rarefaction-wave Riemann solution tends to a two-contact-discontinuity solution to the transportation equations,and the nonvacuum intermediate state between the two rarefaction waves tends to a vacuum state,even when the initial data stays away from the vacuum.As a result,the delta shocks for the transportation equations result from a phenomenon of concentration,while the vacuum states results from a phenomenon of cavitation in the vanishing pressure limit process.These results are completely consistent with that in[26],and also cover those obtained in[2,32,33].
In addition,we also prove that as the pressure tends to the generalized Chaplygin pressure(A →0),any two-shock Riemann solution to the extended Chaplygin gas equations tends to a δ-shock solution to the generalized Chaplygin gas equations,and the intermediate density between the two shocks tends to a weighted δ-measure that forms the δ-shock.Consequently,the delta shocks for the generalized Chaplygin gas equations result from a phenomenon of concentration in the partly vanishing pressure limit process.
From the above analysis,we can find two kinds of occurrence mechanism on the phenomenon of concentration and the formation of delta shock wave.On one hand,since the strict hyperbolicity of the limiting system(1.3)fails,see Section 4,the delta shock wave forms in the limit process as the pressure vanishes. This is consistent with those results obtained in[2,26,29–32].On the other hand,the strict hyperbolicity of the limiting system(1.5)is preserved,see Section 5,the formation of delta shock waves still occur as the pressure partly vanishes.In this regard,it is different from those in[2,26,29–32].In any case,the phenomenon of concentration and the formation of delta shock wave can be regarded as a process of resonance between two characteristic fields.
The paper is organized as follows. In Section 2,we restate the Riemann solutions to transportation equations(1.3)and the generalized Chaplygin gas equations(1.5).In Section 3,we investigate the Riemann problem of the extended Chaplygin gas equations(1.1)–(1.2)and examine the dependence of the Riemann solutions on the two parameters A,B>0.In Section 4,we analyze the limit of Riemann solutions to the extended Chaplygin gas equations(1.1)–(1.2)with(1.6)as the pressure vanishes.In Section 5,we discuss the limit of Riemann solutions to the extended Chaplygin gas equations(1.1)–(1.2)with(1.6)as the pressure approaches to the generalized Chaplygin pressure.Finally,conclusions are drawn and discussions are made in Section 6.
2 Preliminaries
2.1 Riemann Problem for the Transportation Equations
In this section,we restate the Riemann solutions to the transportation equations(1.3)with initial data(1.6),see[14]for more details.
The transportation equations(1.3)have a double eigenvalue λ=u and only one right eigenvectors=(1,0)T.Furthermore,we have,which means that λ is linearly degenerate.The Riemann problem(1.3)and(1.6)can be solved by contact discontinuities,vacuum or δ-shocks connecting two constant states(ρ±,u±).
By taking the self-similar transformation,the Riemann problem is reduced to the boundary value problem of the ordinary differential equations:

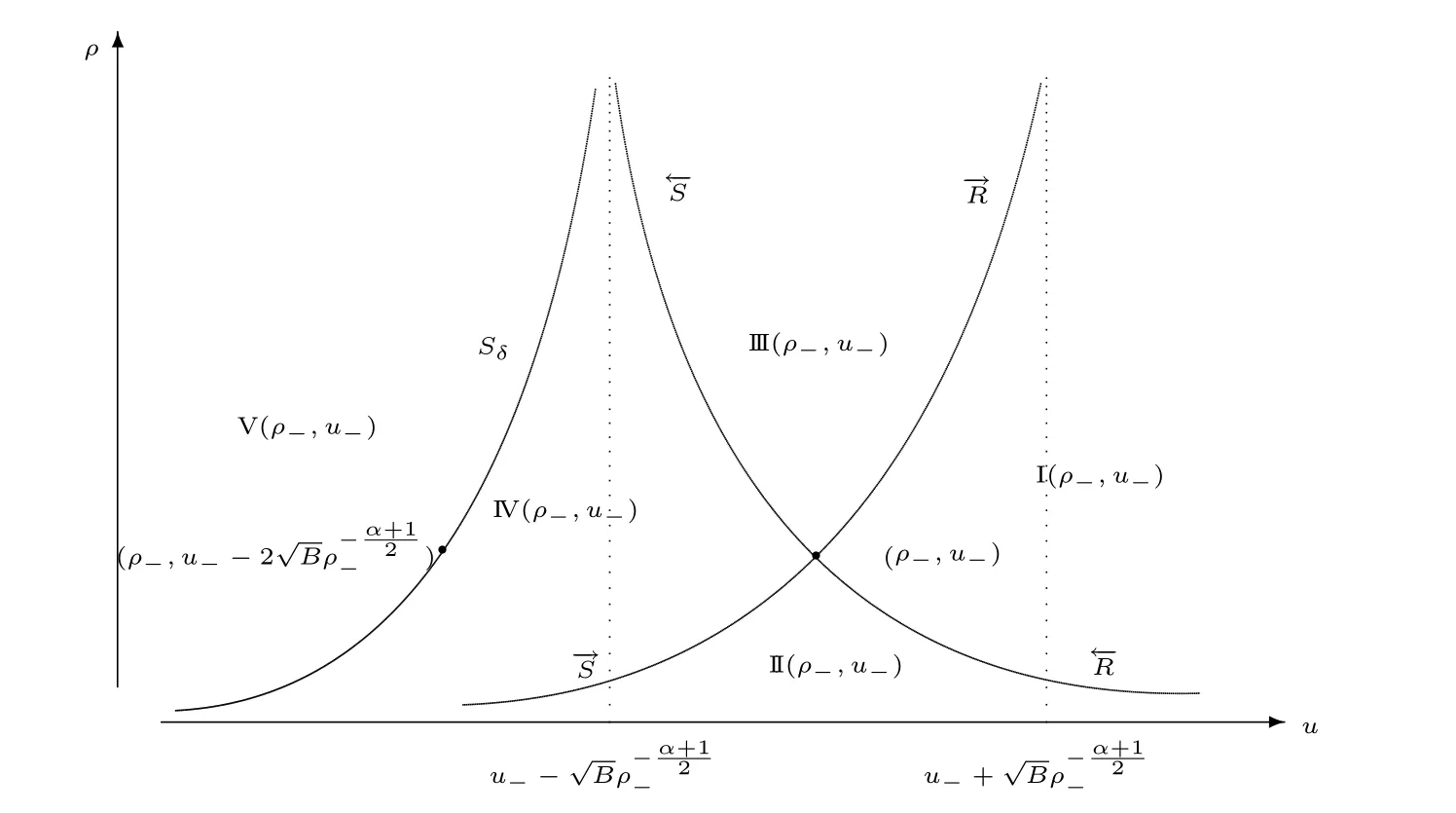
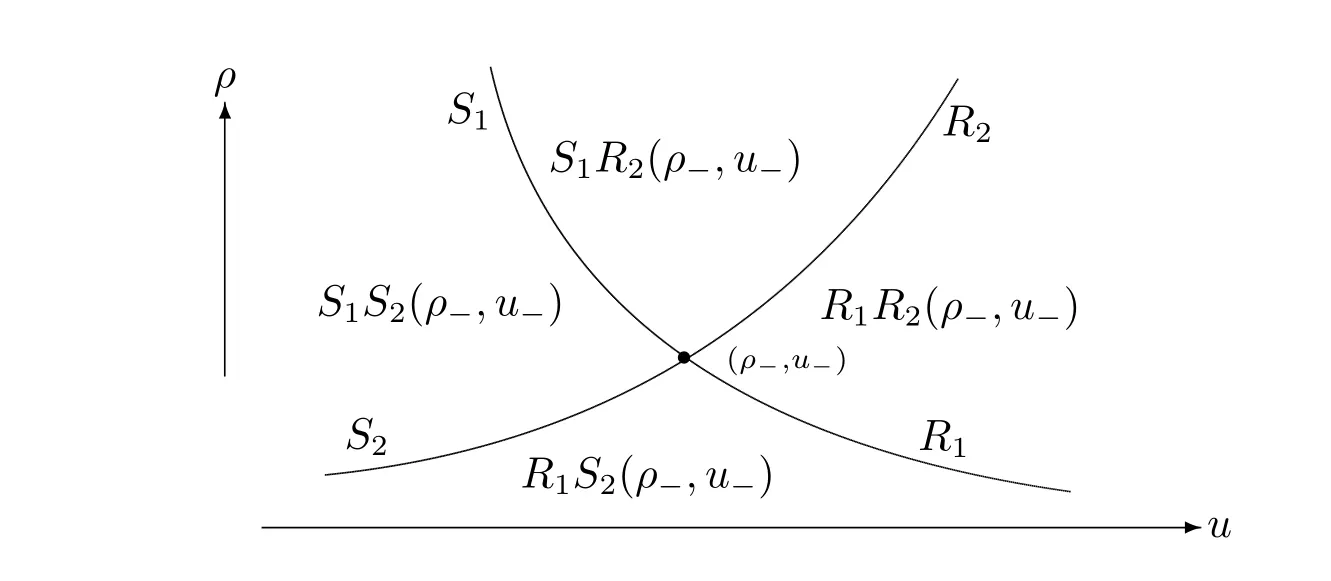
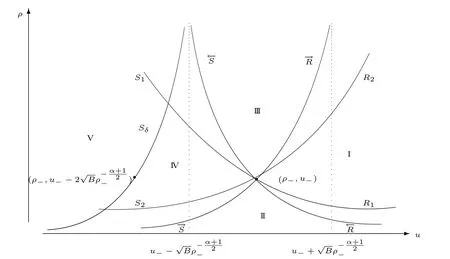
For the case u− For the case u−=u+,it is easy to see that the constant states(ρ±,u±)can be connected by a contact discontinuity. For the case u−>u+,a solution containing a weighted δ-measure supported on a curve will be constructed.Let x=x(t)be a discontinuity curve,we consider a piecewise smooth solution of(1.3)in the form To define the measure solutions,a two-dimensional weighted δ-measure p(s)δSsupported on a smooth curve S={(x(s),t(s)):a in which where and Here,H(x)is the Heaviside function given by H(x)=1 for x>0 and H(x)=0 for x<0. Substituting(2.3)into(2.5),one can derive the generalized Rankine-Hugoniot conditions where[ρ]=ρ+−ρ−,etc. Through solving(2.6)with x(0)=0,w(t)=0,we obtain Moreover,the δ-measure solution(2.3)with(2.7)satisfies the δ-entropy condition which means that all the characteristics on both sides of the δ-shock are incoming. In this section,we solve the Riemann problem for the generalized Chaplygin gas equations(1.5)with(1.6),which one can also see in[35,36]. It is easy to see that(1.5)has two eigenvalues with corresponding right eigenvectors So(1.5)is strictly hyperbolic for ρ>0.Moreover,when 0<α<1,we havei=1,2,which implies thatandare both genuinely nonlinear and the associated waves are rarefaction waves and shock waves.Wheni=1,2,which implies thatandare both linearly degenerate and the associated waves are both contact discontinuities,see[41]. Since system(1.5)and the Riemann initial data(1.6)are invariant under stretching of coordinates(x,t)→(βx,βt)(β is constant),we seek the self-similar solution Then the Riemann problem(1.5)and(1.6)is reduced to the following boundary value problem of the ordinary differential equations Besides the constant solution,it provides the backward rarefaction wave and the forward rarefaction wave When α=1,the backward(forward)rarefaction wave becomes the backward(forward)contact discontinuity. For a bounded discontinuity at ξ=σ,the Rankine-Hugoniot conditions hold: where[ρ]=ρ −ρ−,etc.Together with the Lax shock inequalities,(2.11)gives the backward shock wave and the forward shock wave When α=1,the backward(forward)shock wave becomes the backward(forward)contact discontinuity. with see[34]. By the weak solution definition in Subsection 2.1,for system(1.5),we can get the following generalized Rankine-Hugoniot conditions Then by solving(2.15)with initial data x(0)=0, wB(0)=0,under the entropy condition we can obtain and when ρ+=ρ−. In the phase plane(ρ>0,u ∈R),given a constant state(ρ−,u−),we draw the elementary wave curves(2.9)–(2.10)and(2.12)–(2.13)passing through this point,which are denoted byandrespectively.The backward shock wavehas an asymptotic lineIn addition,we draw a Sδcurve,which is determined by Then,the phase plane can be divided into five parts I(ρ−,u−),II(ρ−,u−),III(ρ−,u−),IV(ρ−,u−)and V(ρ−,u−)(see Fig.1). By the analysis method in the phase plane,one can construct the Riemann solutions for any given(ρ+,u+)as follows: (1)(ρ+,u+)∈I(ρ−,u−): (2)(ρ+,u+)∈II(ρ−,u−): (3)(ρ+,u+)∈III(ρ−,u−): (4)(ρ+,u+)∈IV(ρ−,u−): (5)(ρ+,u+)∈V(ρ−,u−):δ-shock. Fig.1 The(ρ,u)phase plane for the genreralized Chaplygin gas equations(1.5). In this section,we first solve the elementary waves and construct solutions to the Riemann problem of(1.1)–(1.2)with(1.6),and then examine the dependence of the Riemann solutions on the two parameters A,B>0. The eigenvalues of the system(1.1)–(1.2)are with corresponding right eigenvectors Moreover,we have For(1.1)–(1.2)with(1.6)are invariant under uniform stretching of coordinates:(x,t)→(βx,βt)with constant β>0,we seek the self-similar solution Then the Riemann problem(1.1)–(1.2)with(1.6)is reduced to the boundary value problem of the following ordinary differential equations Any smooth solutions of(3.1)satisfies It provides either the constant state solutions(ρ,u)(ξ)=constant,or the rarefaction wave which is a continuous solutions of(3.2)in the form(ρ,u)(ξ).Then,according to[41],for a given left state(ρ−,u−),the rarefaction wave curves in the phase plane,which are the sets of states that can be connected on the right by a 1-rarefaction wave or 2-rarefaction wave,are as follows and From(3.3)and(3.4),we obtain that which implies that the velocity of 1-rarefaction(2-rarefaction)waveis monotonic decreasing(increasing)with respect to ρ. and For the 1-rarefaction wave,through differentiating u respect to ρ in the second equation in(3.7),we get Thus,it is easy to get uρρ>0 for 1 ≤n ≤3,i.e.,the 1-rarefaction wave is convex for 1 ≤n ≤3 in the upper half phase plane(ρ>0). In addition,from the second equation of(3.7),we have By a similar computation,we have that,for the 2-rarefaction wave,uρ>0,uρρ<0 for 1 ≤n ≤3 andThus,we can draw the conclusion that the 2-rarefaction wave is concave for 1 ≤n ≤3 in the upper half phase plane(ρ>0). Now we consider the discontinuous solution.For a bounded discontinuity at ξ=σ,the Rankine-Hugoniot condition holds where[ρ]=ρ+−ρ−,etc. Eliminating σ from(3.11),we obtain Using the Lax entropy condition,the 1-shock satisfies while the 1-shock satisfies From the first equation in(3.11),we have Thus,by a simple calculation,(3.13)is equivalent to and(3.14)is equivalent to (3.16)and(3.17)imply that ρ>ρ−,u Through the above analysis,for a given left state(ρ−,u−),the shock curves in the phase plane,which are the sets of states that can be connected on the right by a 1-shock or 2-shock,are as follows and For the 1-shock wave,through differentiating u respect to ρ in the second equation in(3.18),we get which means that uρ<0 for the 1-shock wave and that the 1-shock wave curve is starlike with respect to(ρ−,u−)in the region ρ>ρ−.Similarly,we can get uρ>0 for the 2-shock wave and that the 2-shock wave curve is starlike with respect to(ρ−,u−)in the region ρ<ρ−.In addition,it is easy to check thatu=−∞for the 1-shock wave andfor the 2-shock wave. Through the analysis above,for a given left state(ρ−,u−),the sets of states connected with(ρ−,u−)on the right in the phase plane consist of the 1-rarefaction wave curve R1(ρ−,u−),the 2-rarefaction wave curve R2(ρ−,u−),the 1-shock curve S1(ρ−,u−)and the 2-shock curve S2(ρ−,u−).These curves divide the upper half plane into four parts R1R2(ρ−,u−),R1S2(ρ−,u−),S1R2(ρ−,u−)and S1S2(ρ−,u−). Now,we put all of these curves together in the upper half plane(ρ>0,u ∈R)to obtain a picture as Fig.2. By the phase plane analysis method,it is easy to construct Riemann solutions for any given right state(ρ+,u+)as follows (1)(ρ+,u+)∈R1R2(ρ−,u−):R1+R2; (2)(ρ+,u+)∈R1S2(ρ−,u−):R1+S2; (3)(ρ+,u+)∈S1R2(ρ−,u−):S1+R2; (4)(ρ+,u+)∈S1S2(ρ−,u−):S1+S2. Fig.2 The(ρ,u)phase plane for the extended Chaplygin gas equations(1.1)–(1.2). In this section,we will study the vanishing pressure limit process,i.e.,A,B →0.Since the two regions S1R2(ρ−,u−)and R1S2(ρ−,u−)in the(ρ,u)plane have empty interior when A,B →0,it suffices to analyze the limit process for the two cases(ρ+,u+)∈S1S2(ρ−,u−)and(ρ+,u+)∈R1R2(ρ−,u−). First,we analyze the formation of δ-shocks in Riemann solutions to the extended Chaplygin gas equations(1.1)–(1.2)with(1.6)in the case(ρ+,u+)∈S1S2(ρ−,u−)as the pressure vanishes. When(ρ+,u+)∈S1S2(ρ−,u−),for fixed A,B>0,letbe the intermediate state in the sense that(ρ−,u−)andare connected by 1-shock S1with speedand(ρ+,u+)are connected by 2-shock S2with speed.Then it follows In the following,we give some lemmas to show the limit behavior of the Riemann solutions of system(1.1)–(1.2)with(1.6)as A,B →0. Lemma 4.1 ProofEliminatingin the second equation of(4.1)and(4.2)gives By Lemma 4.1,from(4.3)we immediately have the following lemma. Lemma 4.2 Lemma 4.3 ProofFrom the first equation of(4.1)and(4.2)for S1and S2,by Lemma 4.1,we have From the second equation of(4.1),by Lemmas 4.1–4.2,we get The proof is completed. Lemma 4.4 ProofHere we only prove the case for.The first equation of the Rankine-Hugoniot condition(3.11)for S1and S2read from which we have Similarly,from the second equations of the Rankine-Hugoniot condition(3.11)for S1and S2, we obtain Thus,from(4.8)and(4.10)we immediately get(4.5)and(4.6).For the case ρ+=ρ−,the conclusion is obviously true,so we omit it.The proof is finished. The above Lemmas 4.1–4.4 show that,as A,B →0,the curves of the shock wave S1and S2will coincide and the delta shock waves will form.Next we will arrange the values which give the exact position,propagation speed and strength of the delta shock wave according to Lemmas 4.3 and 4.4. From(4.5)and(4.6),we let then From(4.11)–(4.14),we can see that the quantities defined above are exactly consistent with those given by(2.7). Thus,it uniquely determines that the limits of the Riemann solutions to system(1.1)–(1.2)and(1.6)when A,B →0 in the case(ρ+,u+)∈IV and u−>u+is just the delta shock solution of(1.3)and(1.6).So we get the following results which characterizes the vanishing pressure limit in the case(ρ+,u+)∈IV and u−>u+. Theorem 4.1If u−>u+,for each fixed A,B,(ρ+,u+)∈IV,assuming that(ρAB,uAB)is a two-shock wave solution of(1.1)–(1.2)and(1.6)which is constructed in Section 3,it is obtained that when A,B →0,(ρAB,uAB)converges to a delta shock wave solution to the transportation equations(1.3)with the same initial data. In this subsection,we show the formation of vacuum states in the Riemann solutions to(1.1)–(1.2)with(1.6)in the case(ρ+,u+)∈R1R2(ρ−,u−)with u− At this moment,for fixed A,B>0,letbe the intermediate state in the sense that(ρ−,u−)andare connected by 1-rarefaction wave R1with speedand(ρ+,u+)are connected by 2-rarefaction wave R2with speed. Then it follows Now,from the second equations of(4.15)and(4.16),using the following integral identity it follows that the intermediate statesatisfies which implies the following result. Theorem 4.2Let u− Fig.3 The(ρ,u)phase plane for the generalized Chaplygin gas equations(1.5)and the extended Chaplygin gas equations(1.1)–(1.2). Lemma 5.1When(ρ+,u+)∈V(ρ−,u−),there exists a positive parameter A0such that(ρ+,u+)∈S1S2(ρ−,u−)when 0 ProofFrom(ρ+,u+)∈V(ρ−,u−),we have then All the states(ρ,u)connected with(ρ−,u−)by a backward shock wave S1or a forward shock wave S2satisfy or When ρ+=ρ−,the conclusion is obviously true.Whenby taking we have which together with(5.2)gives the conclusion.The proof is completed. When 0 and Lemma 5.2 ProofEliminatingin the second equation of(5.7)and(5.8)gives which contradicts with(5.2).Therefore we must haveThe proof is completed. By Lemma 5.2,from(5.9)we immediately have the following lemma. Lemma 5.3 Lemma 5.4Letthen ProofFrom the second equation of(5.7)for S1,by Lemmas 4.2 and 4.3,we have Similarly,from the second equation of(5.8)for S2,we have Furthermore,similar to the analysis in Lemma 4.3,we can obtainThe proof is completed. Lemma 5.5Formentioned in Lemma 5.4, as ρ+=ρ−. ProofLettingby Lemma 5.4,from(5.12)and(5.13)we have which leads to Eliminating L from(5.16)and(5.17),we have Similar to Lemma 4.4,we have the following lemma. Lemma 5.6 ProofHere we only prove the case for.Similar to the proof of Lemma 4.4,taking account into(3.11)and(5.18),we have and So For the case ρ+=ρ−,the conclusion is obviously true,so we omit it.The proof is finished. The above Lemmas 5.1–5.6 show that,as A →0,the curves of the shock waveandwill coincide and the delta shock waves will form.Next,we will arrange the values which give the exact position,propagation speed and strength of the delta shock wave according to Lemmas 5.4 and 5.6. then which is equal to σB(t).Furthermore,by lettingwe have From(5.23)–(5.26),we can see that the quantities defined above are exactly consistent with those given by(2.17)–(2.20).When ρ+=ρ−,similar results can be obtained.Thus,it uniquely determines that the limits of Riemann solutions to system(1.1)–(1.2)and(1.6)when A →0 in the case(ρ+,u+)∈V and u−>u+is just the delta shock solution of(1.5)and(1.6).So we get the following results which characterizes the vanishing pressure limit in the case(ρ+,u+)∈V and u−>u+. Theorem 5.1If u−>u+,for each fixed A,B,(ρ+,u+)∈V,assuming that(ρA,uA)is a two-shock wave solution of(1.1)–(1.2)and(1.6)which is constructed in Section 3,it is obtained that when A →0,(ρA,uA)converges to a delta shock wave solution to the generalized Chaplygin gas equations(1.5)with the same initial data. In this paper,we have considered two kinds of flux approximation limits of Riemann solutions to the extended Chaplygin gas equations and studied the concentration and the formation of delta shocks during the limit process.Moreover,we have proved that the vanishing pressure limit of Riemann solutions to extended Chaplygin gas equations is just the corresponding ones to transportation equations,and when the extended Chaplygin pressure approaches the generalized Chaplygin pressure,the limit of Riemann solutions to the extended Chaplygin gas equations is just the corresponding ones to the generalized Chaplygin gas equations. On the other hand,recently,Shen and Sun have studied the Riemann problem for the nonhomogeneous transportation equations,and the nonhomogeneous(generalized)Chaplygin gas equations with coulomb-like friction,see[38,39,42]. Similarly,we will also consider the Riemann problem for the nonhomogeneous extended Chaplygin gas equations with coulomb-like friction.Furthermore,we will consider the formation of delta shock waves in its flux approximation limit and analyze the relations of Riemann solutions among the nonhomogeneous extended Chaplygin gas equations,the nonhomogeneous generalized Chaplygin gas equations and the nonhomogeneous transportation equations.These will be left for our future work.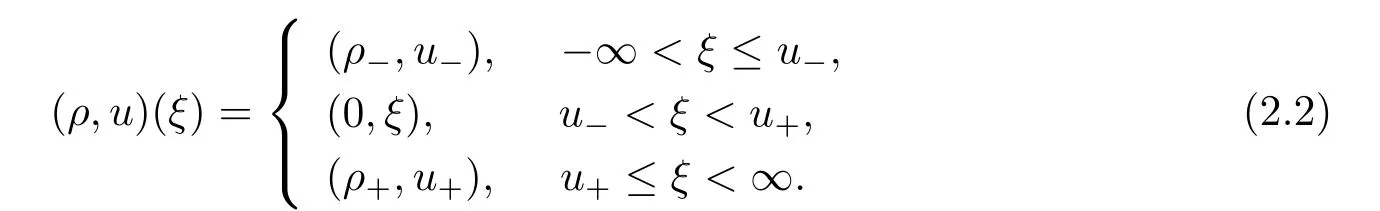
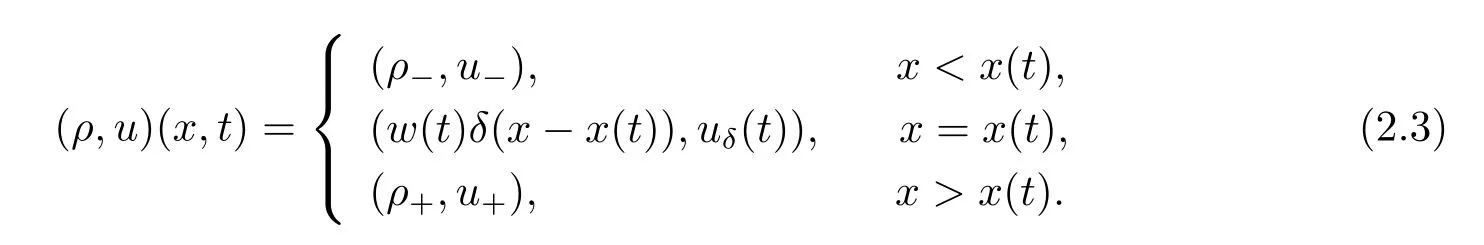
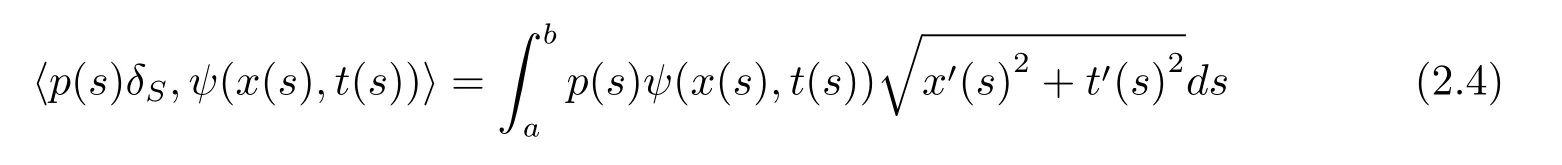
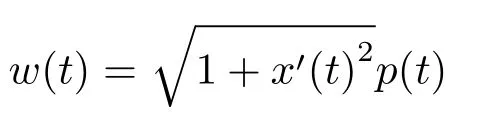

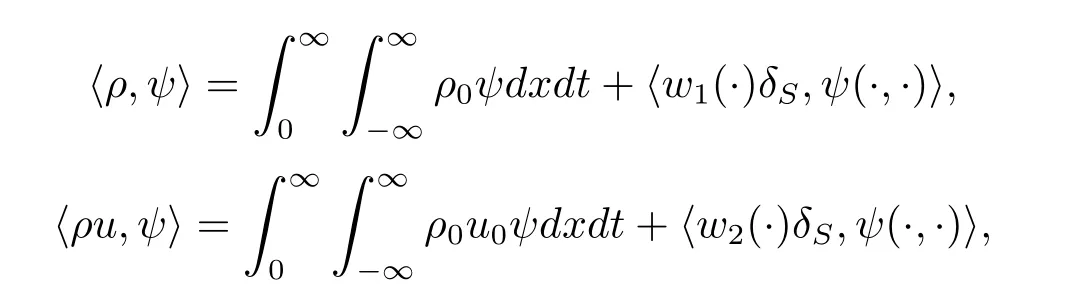
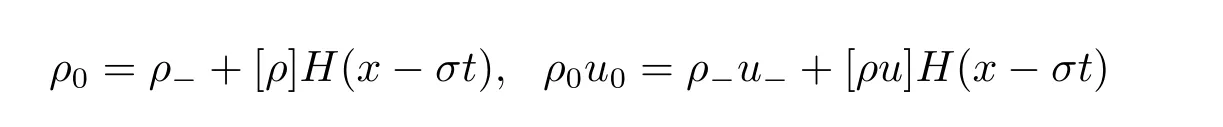
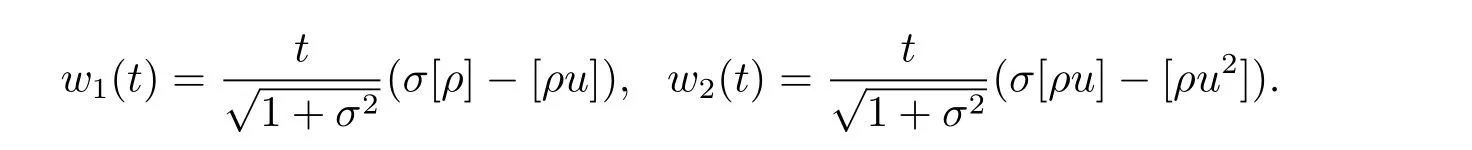
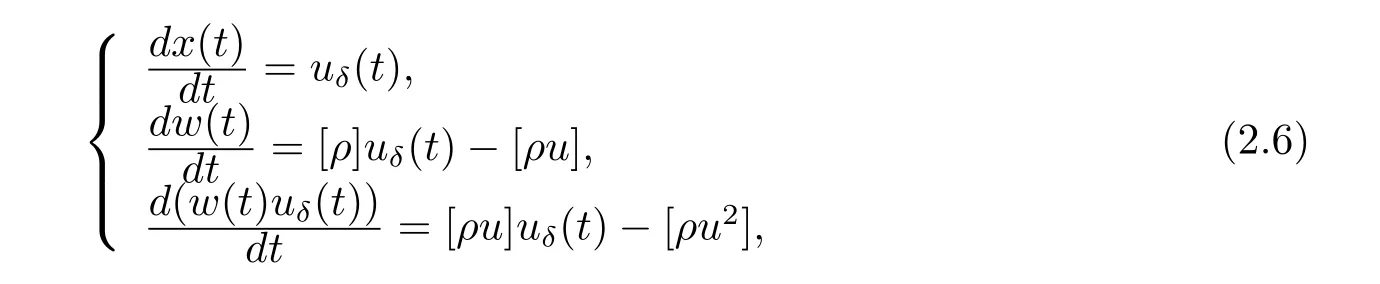
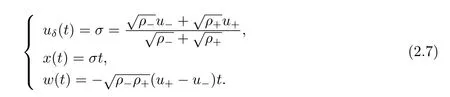
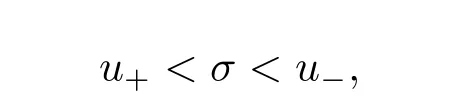
2.2 Riemann Problem for the Generalized Chaplygin Gas Equations
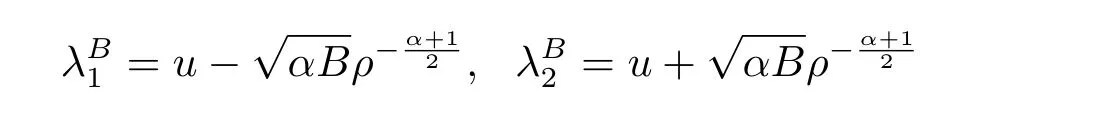

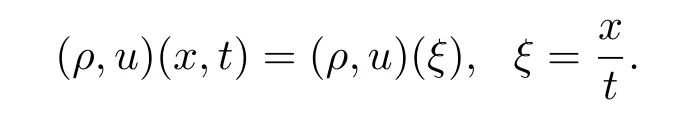
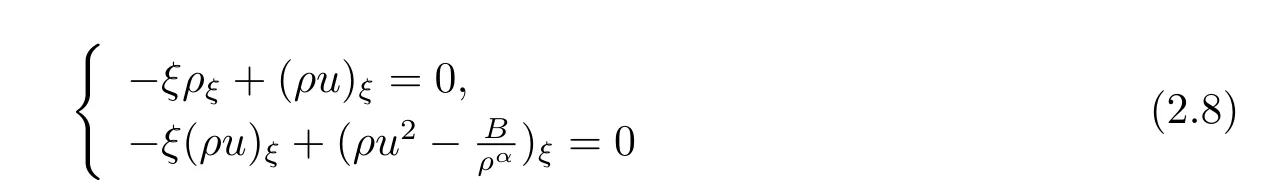
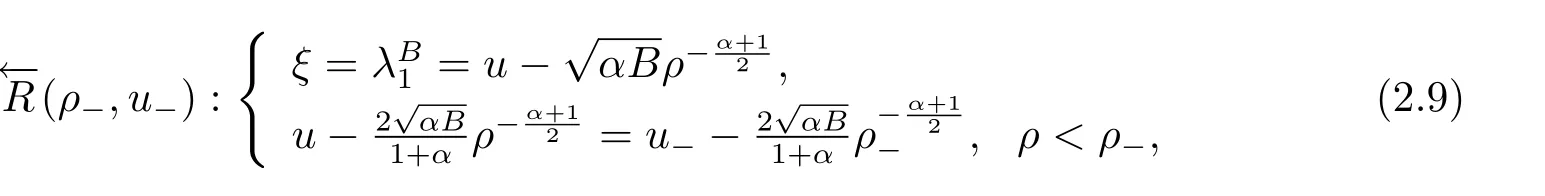
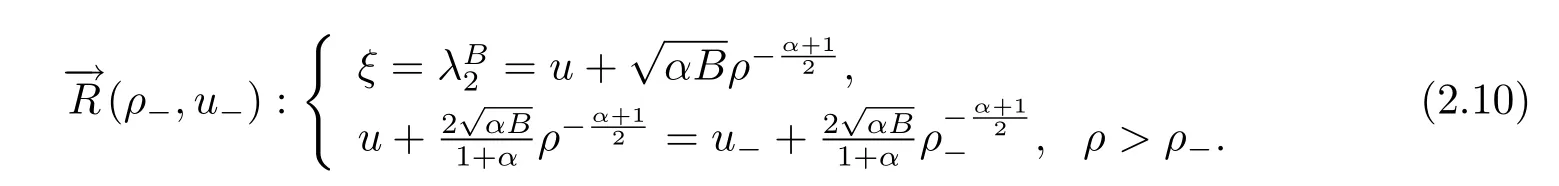
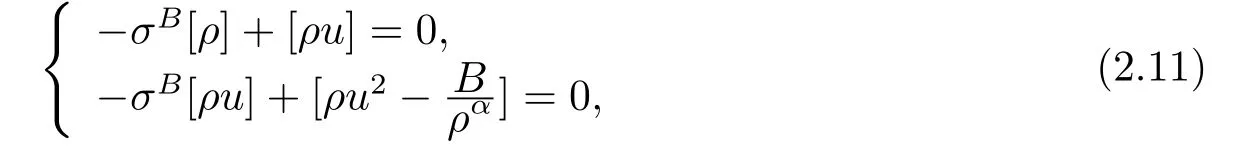
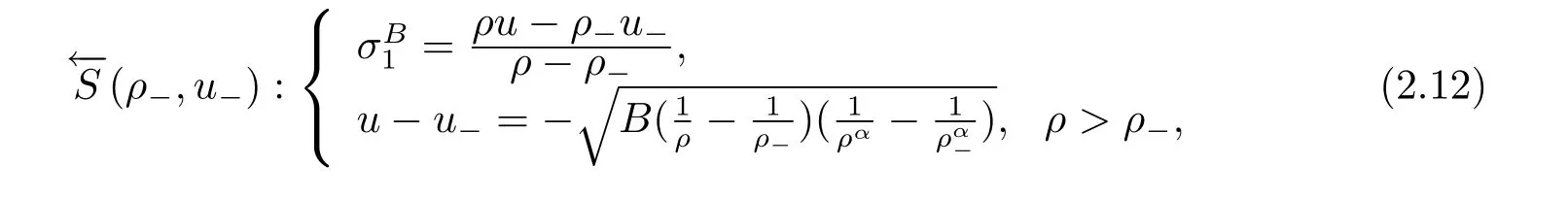
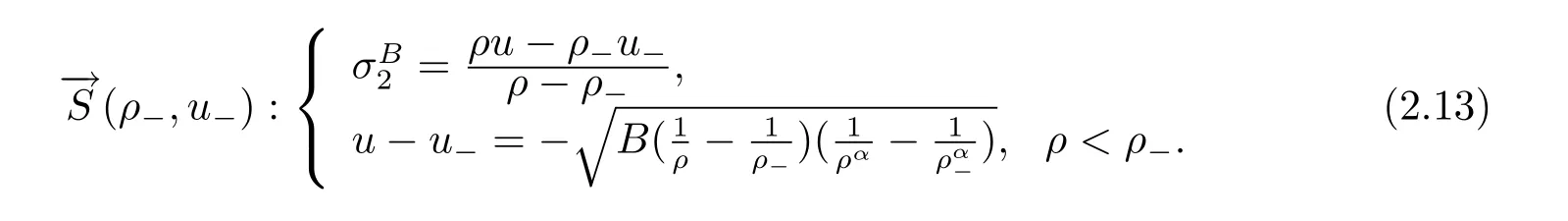
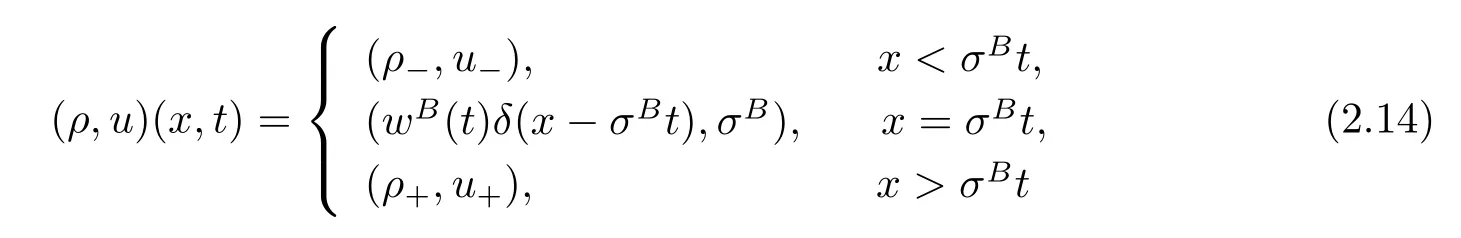
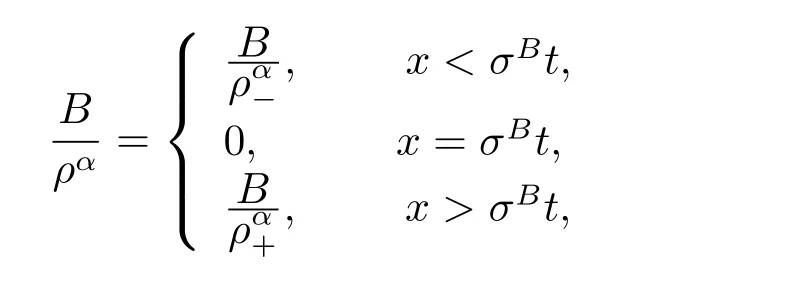

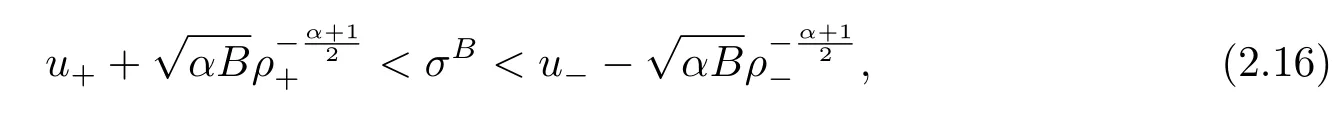
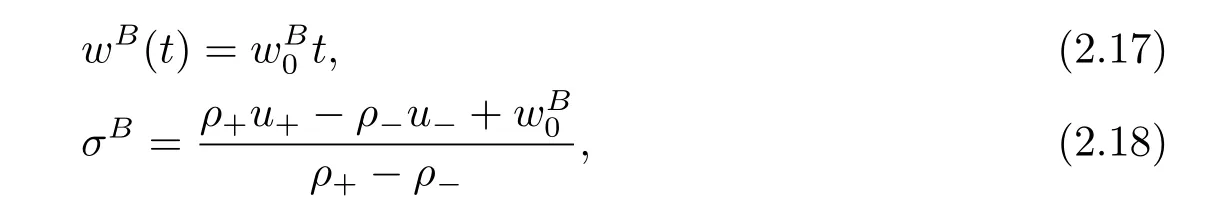
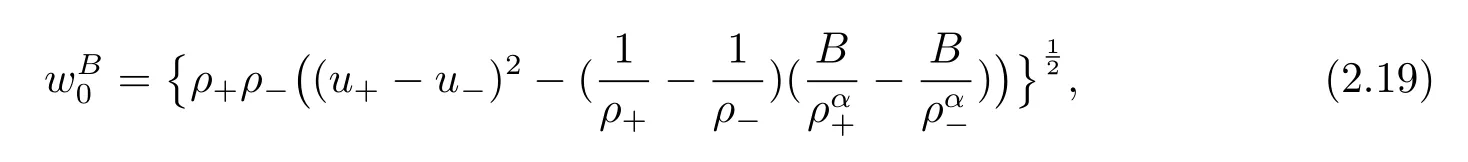
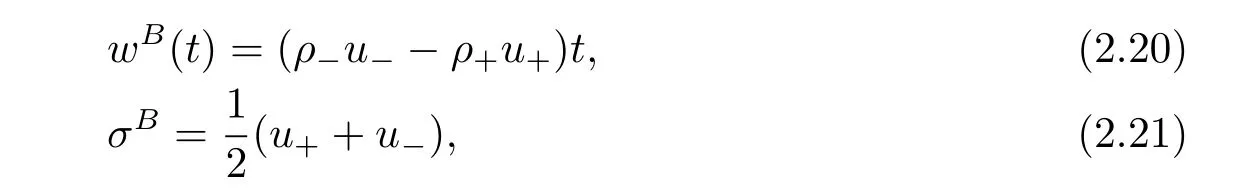
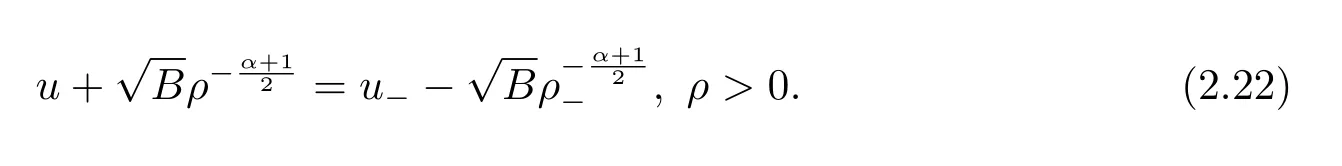
3 Riemann Problem for the Extended Chaplygin Gas Equations
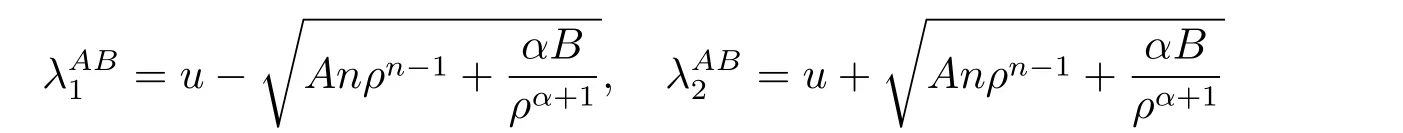
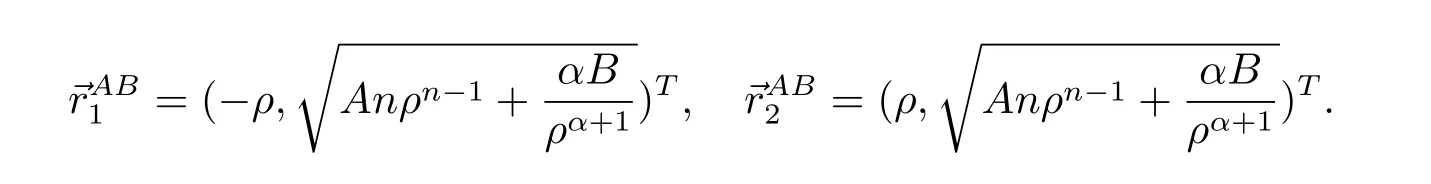
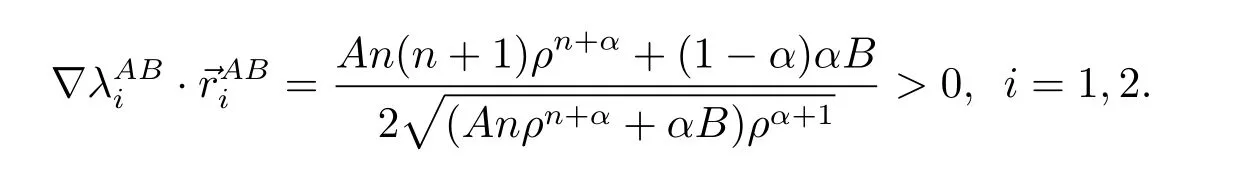
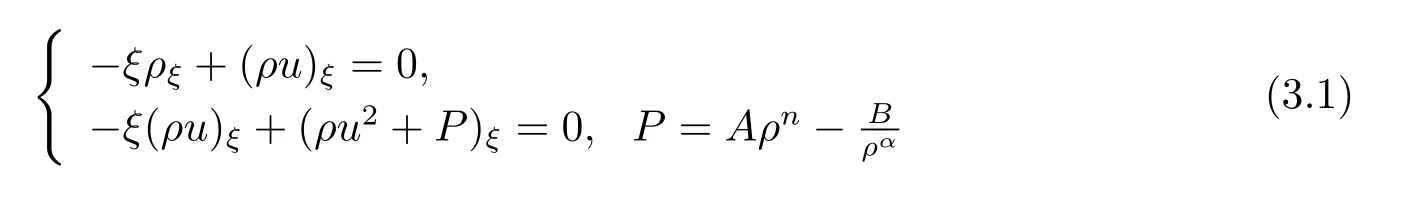
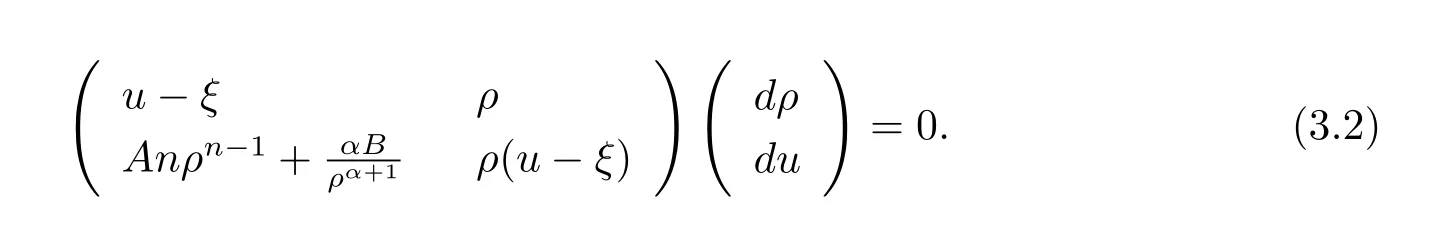
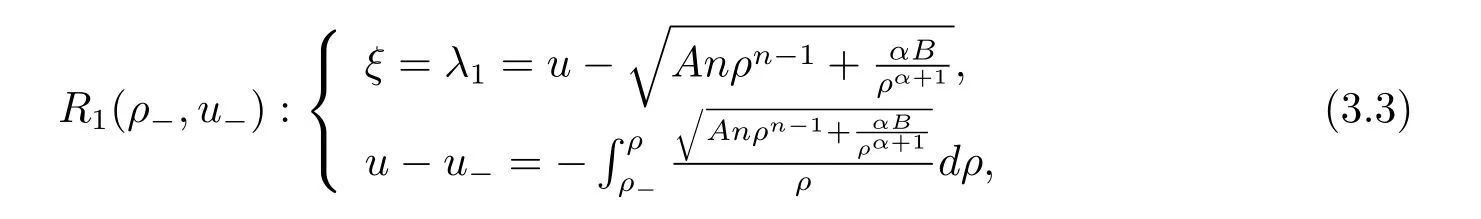
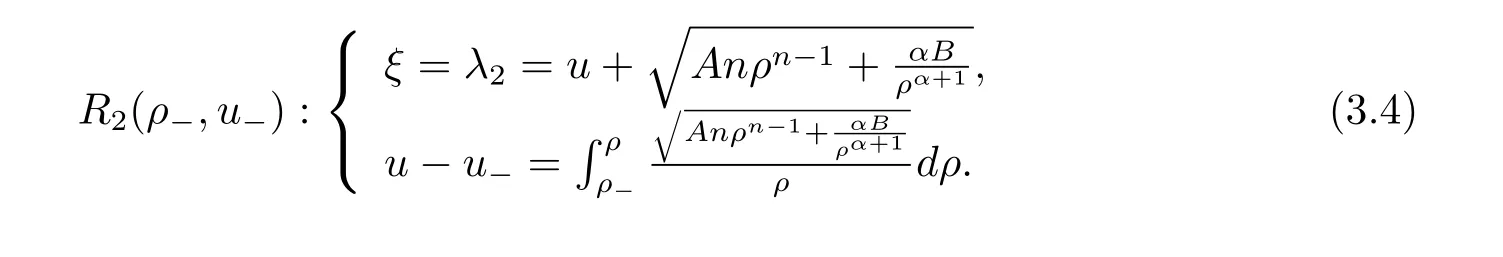
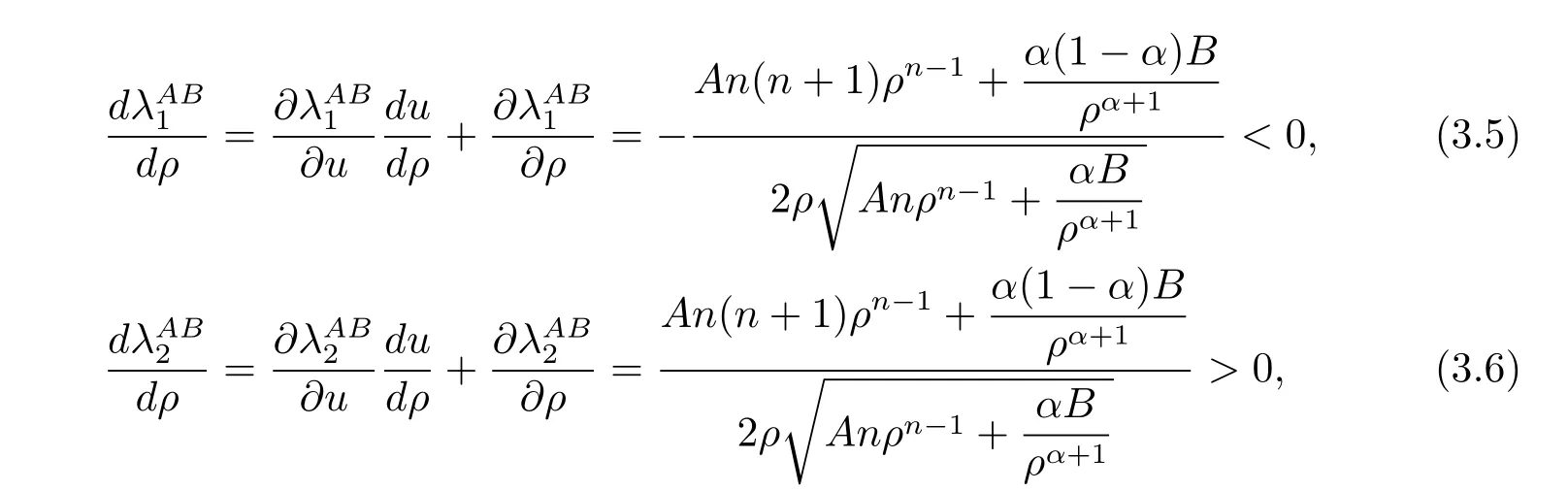
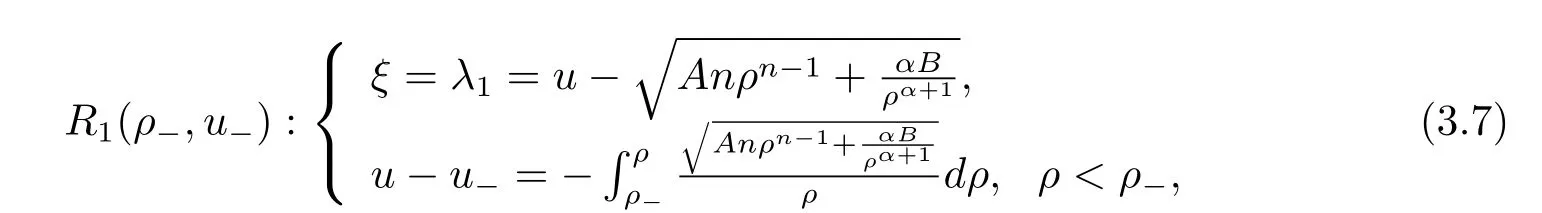
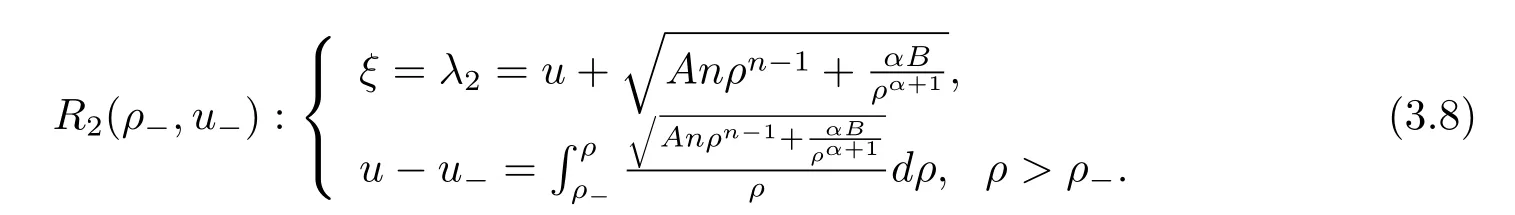
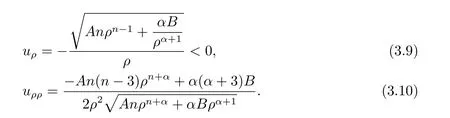
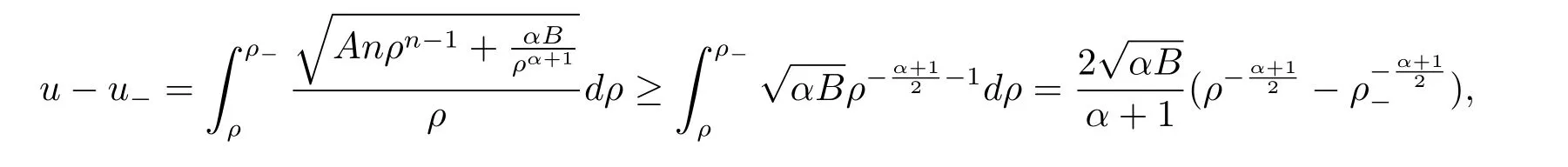
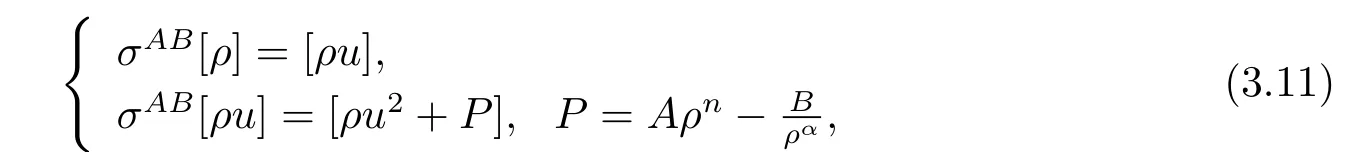
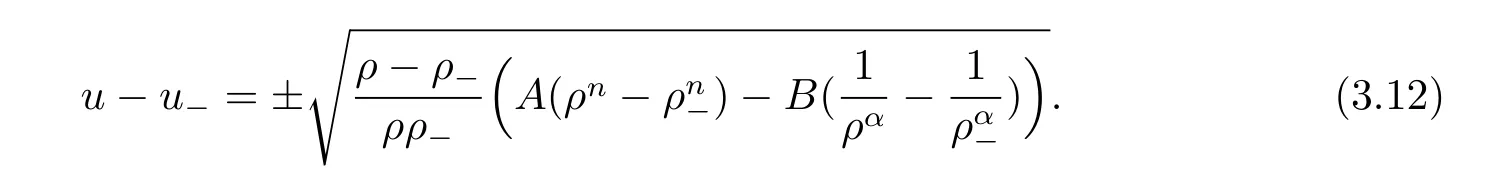
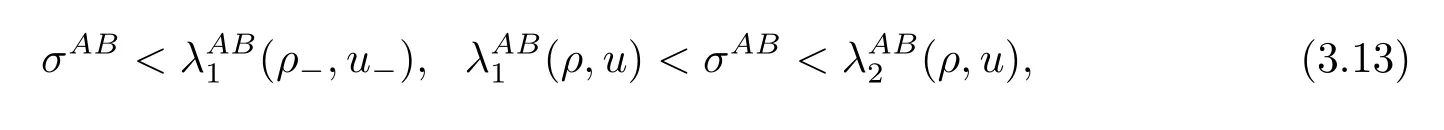
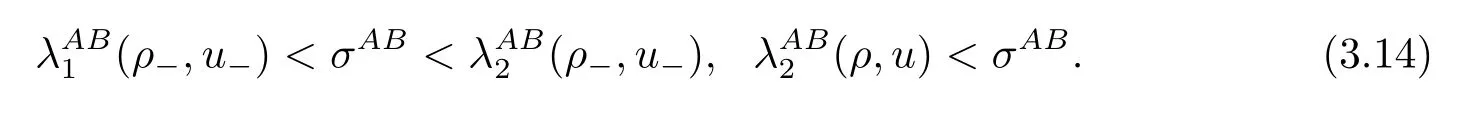
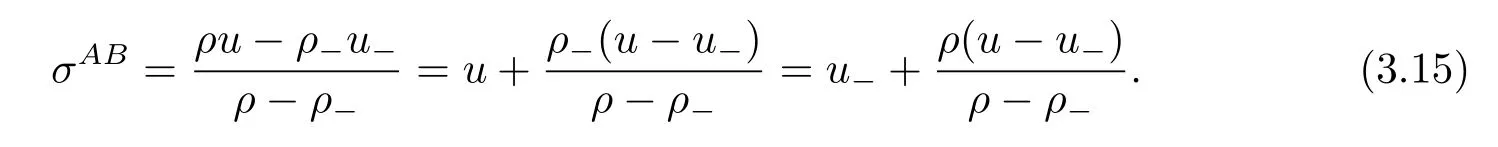
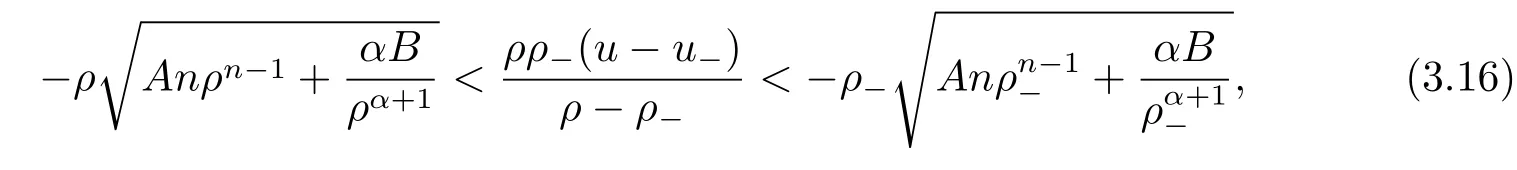
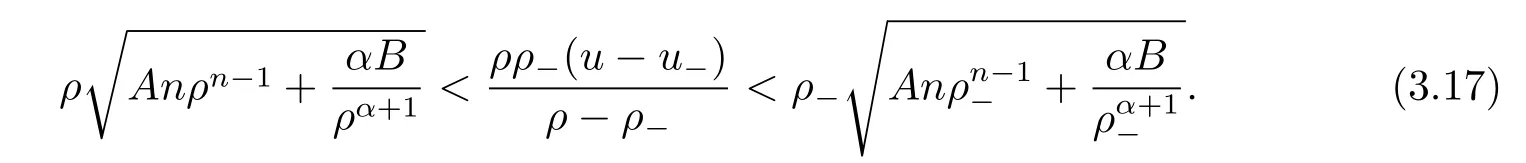
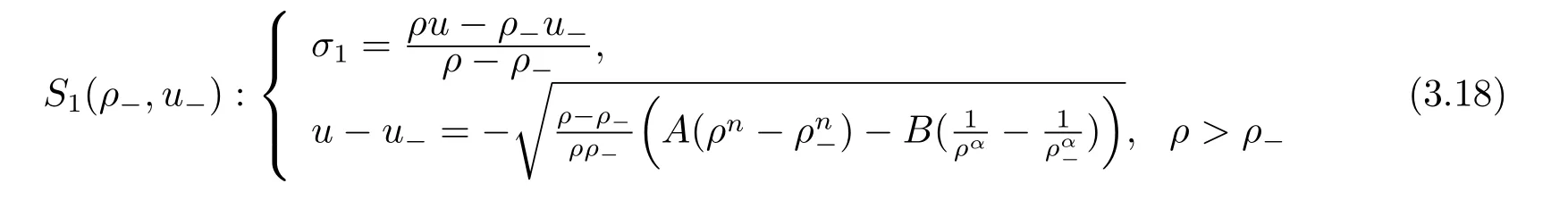

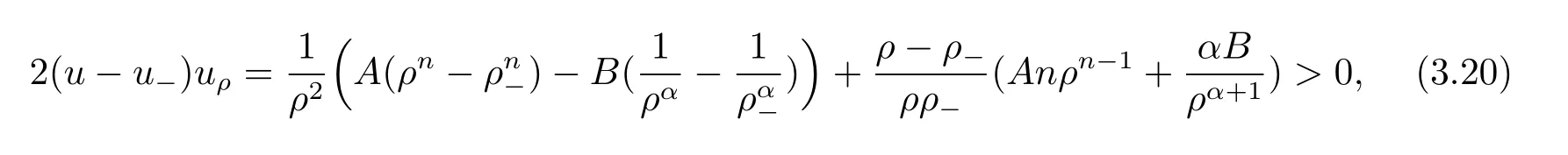
4 Formation of δ-Shocks and Vacuum States as A,B →0
4.1 δ-Shocks and Concentration
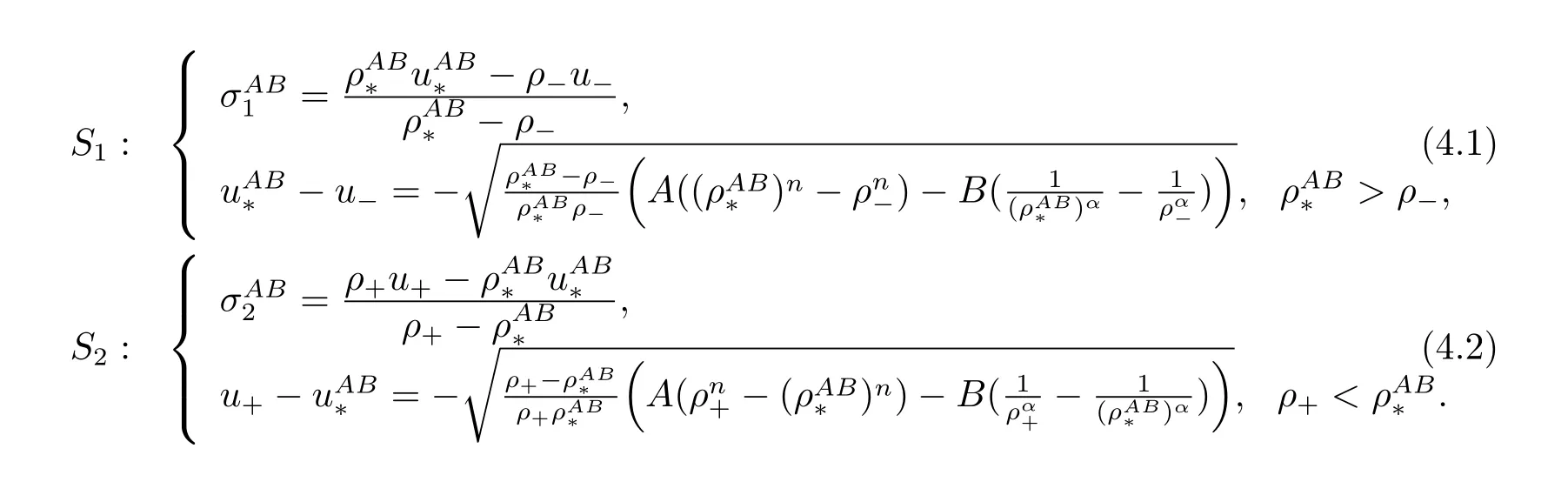
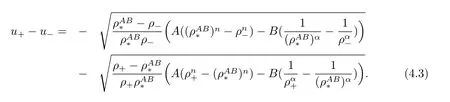
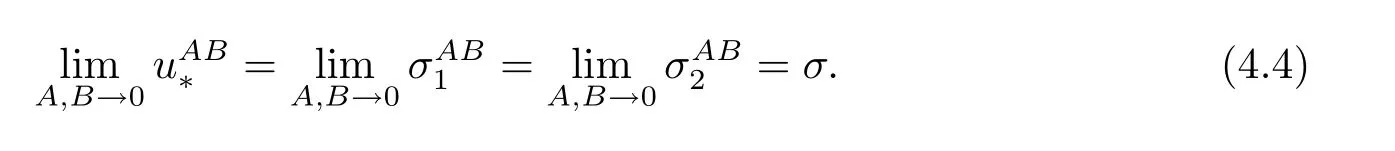
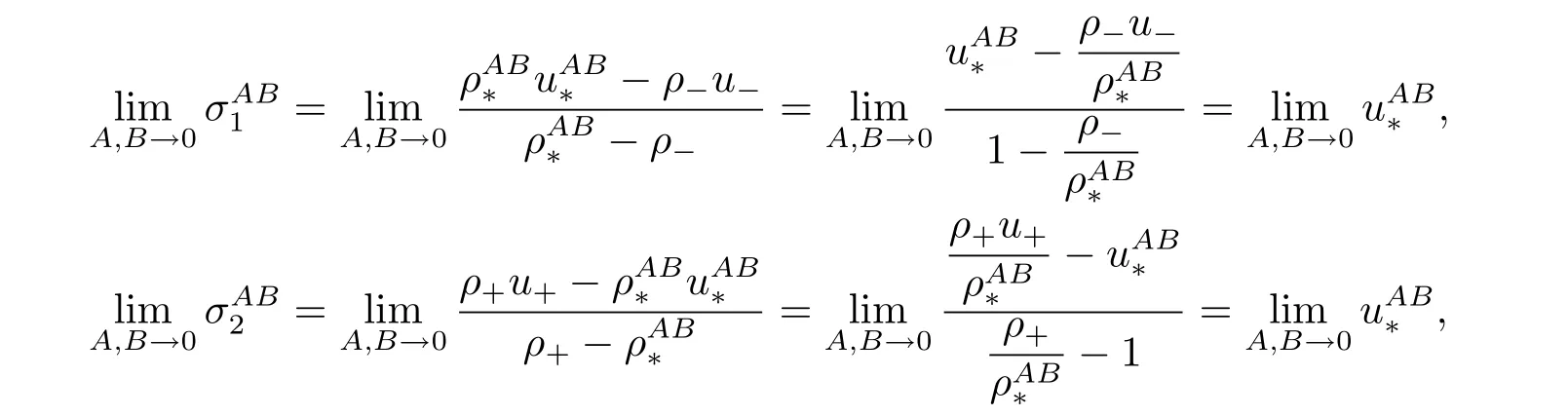
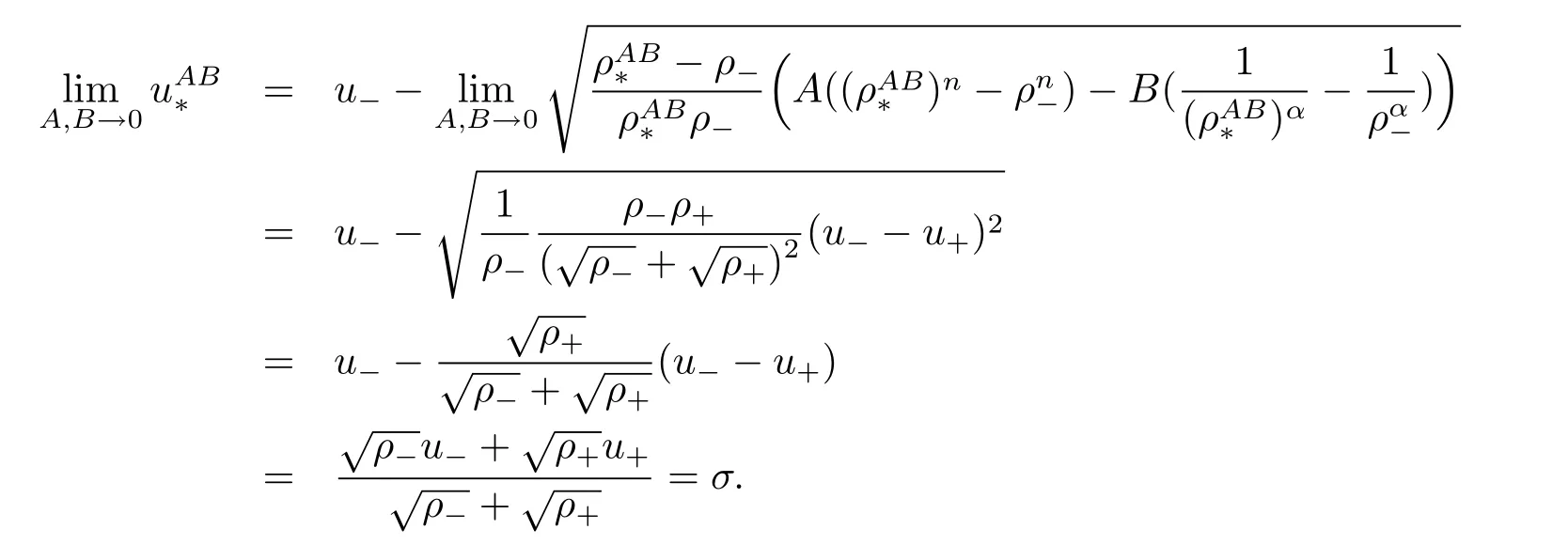
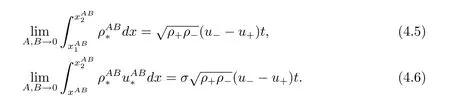
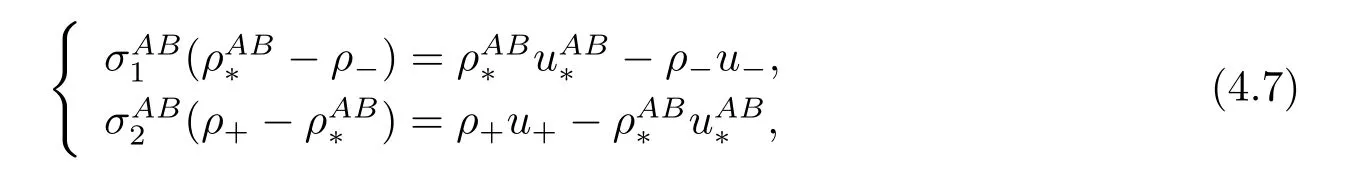
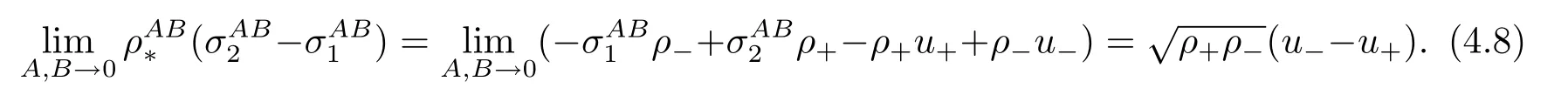
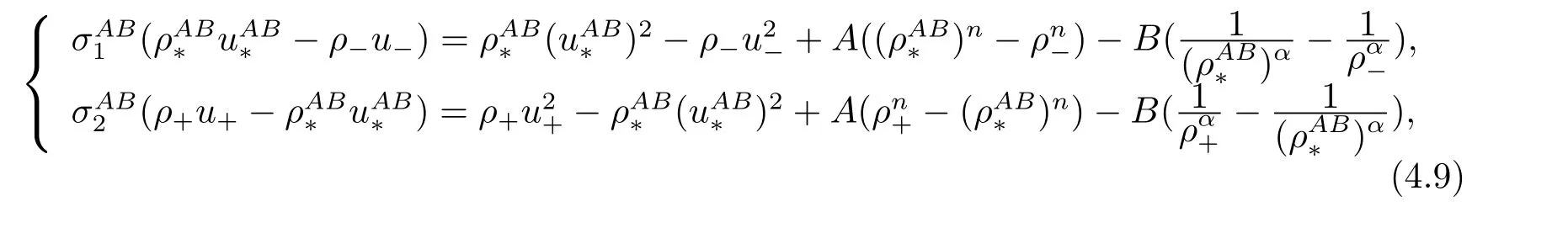
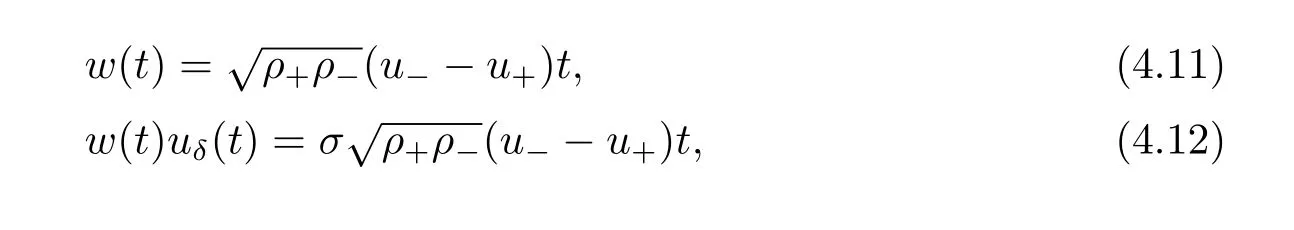


4.2 Formation of Vacuum States

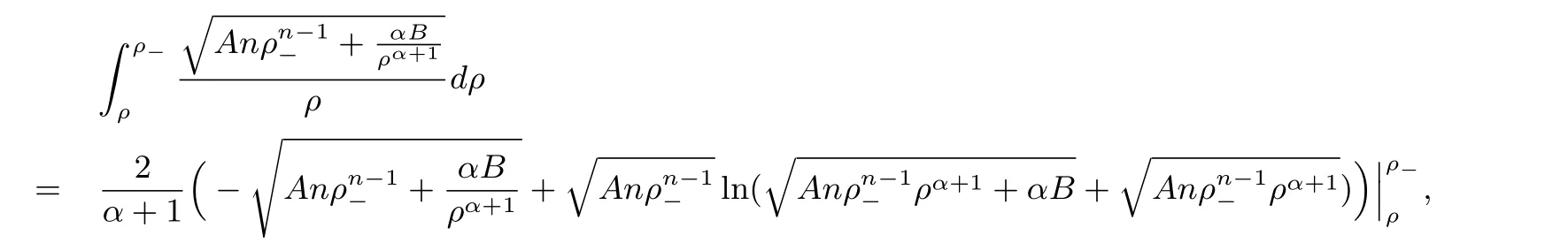

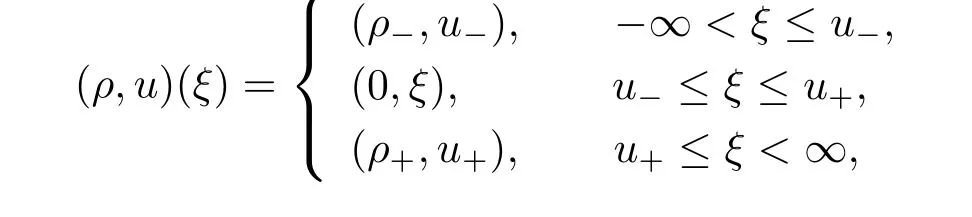
5 Formation of δ-Shocks as A →0
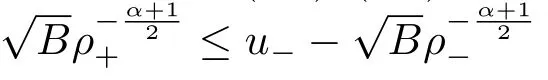
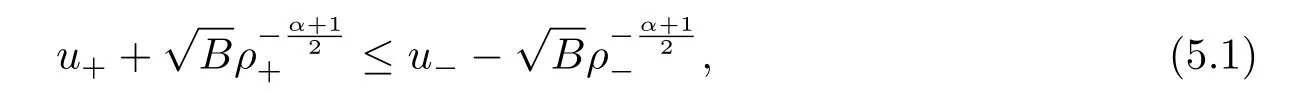
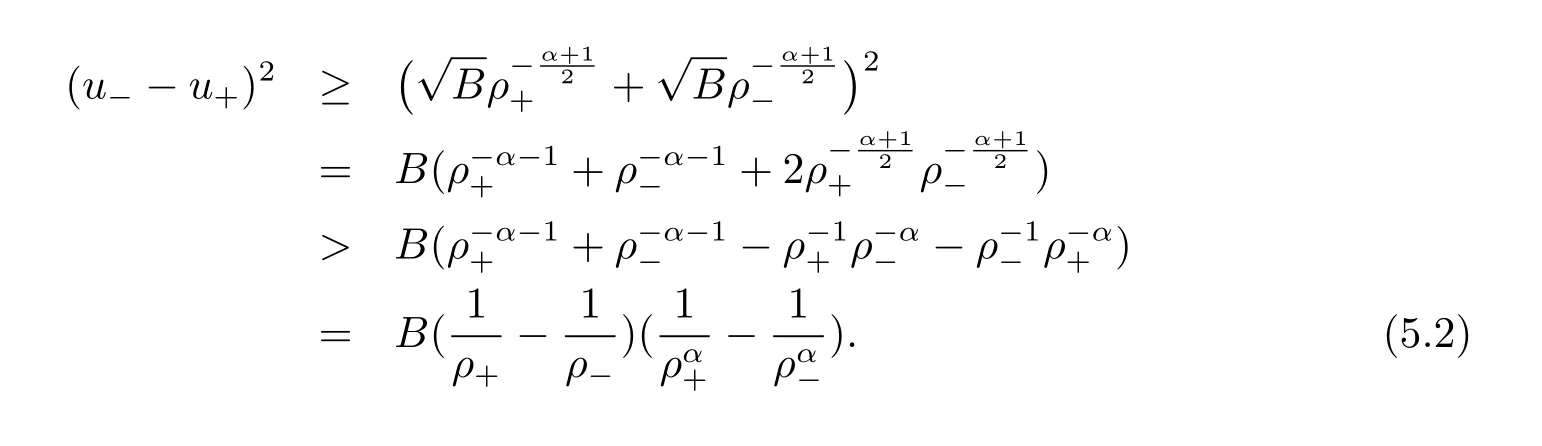
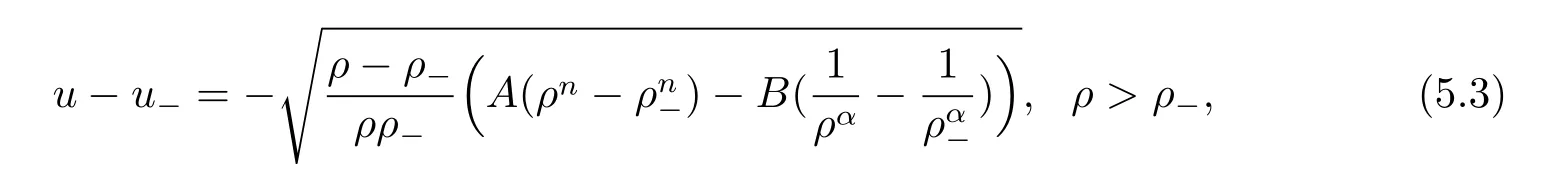
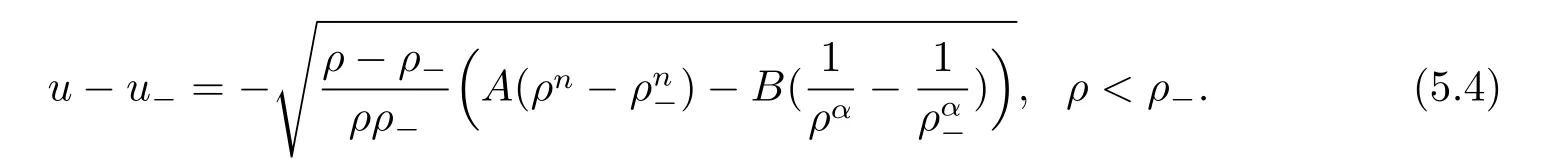
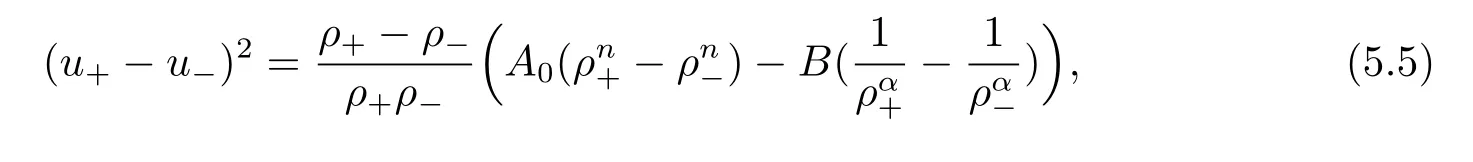
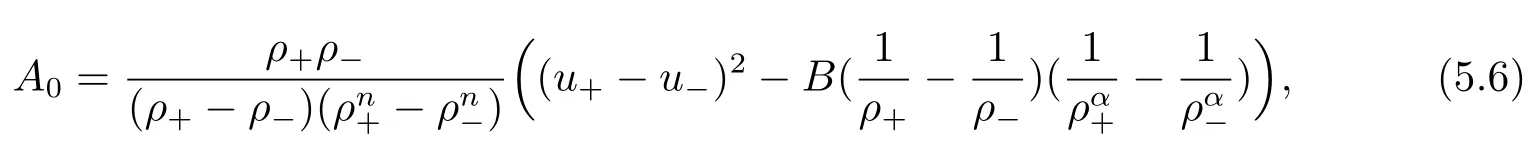
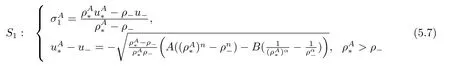
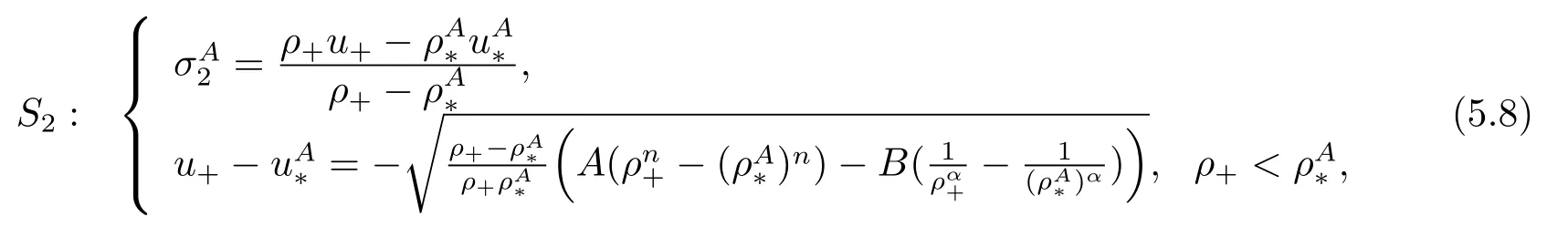
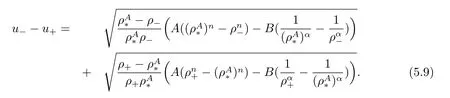
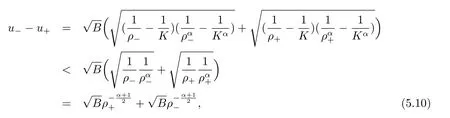
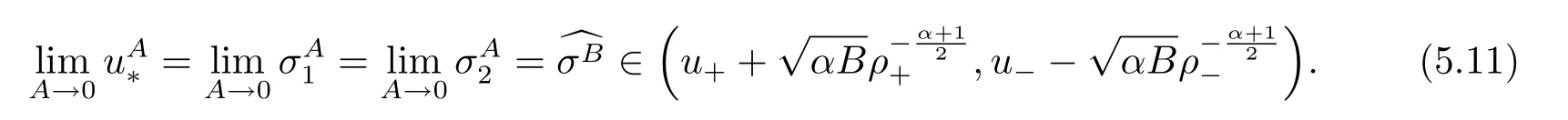
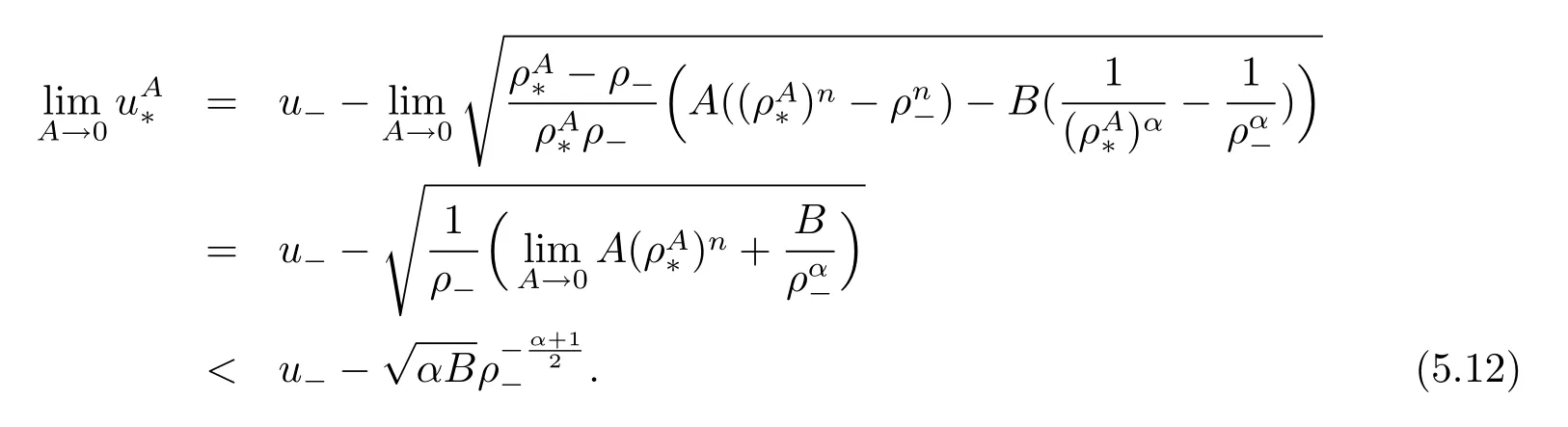
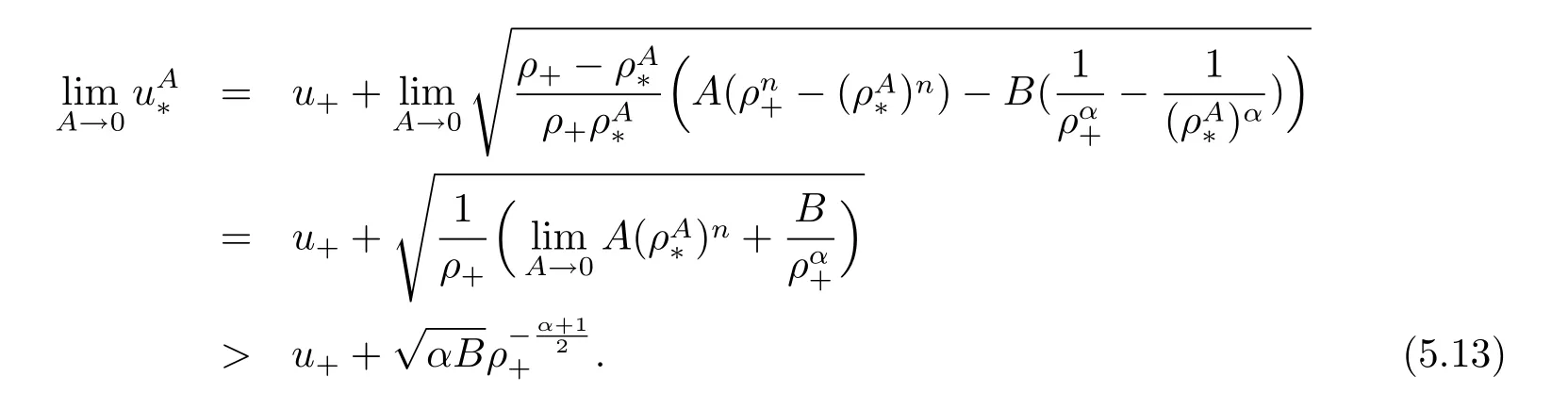
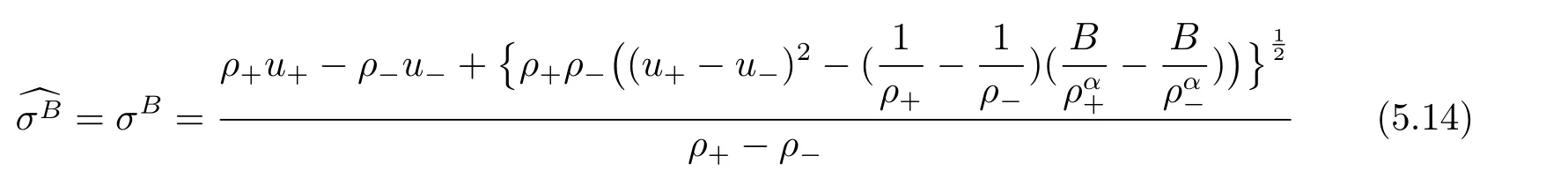

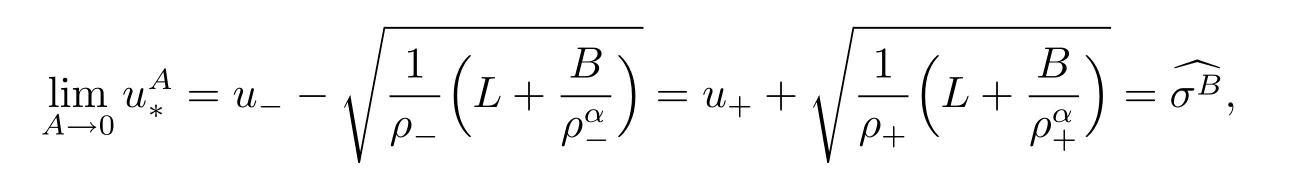
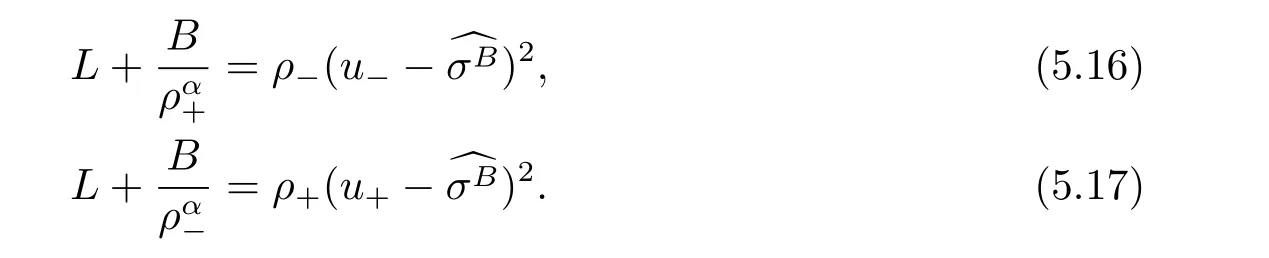
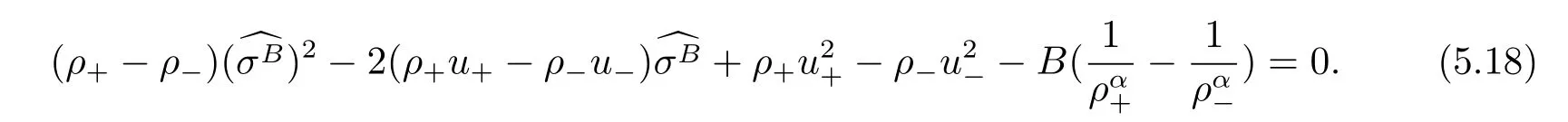
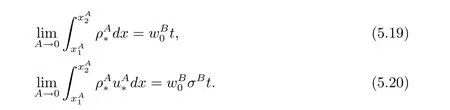
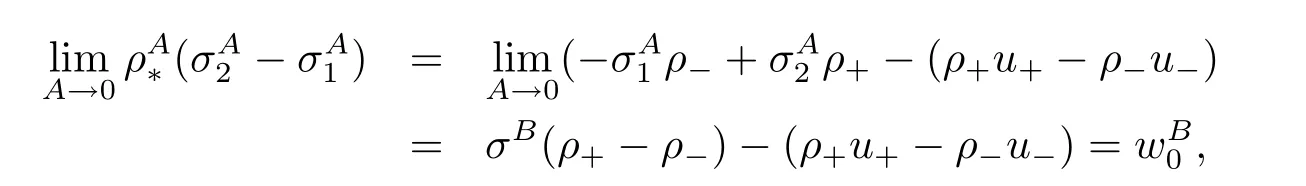
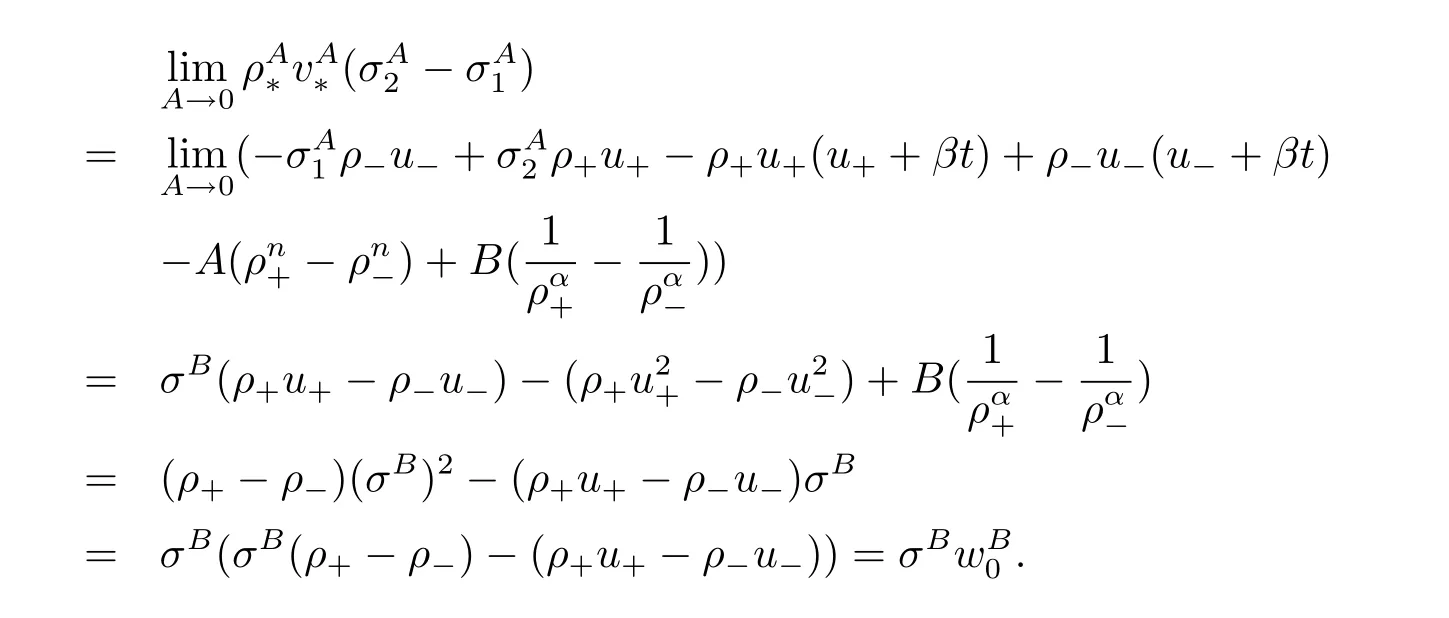
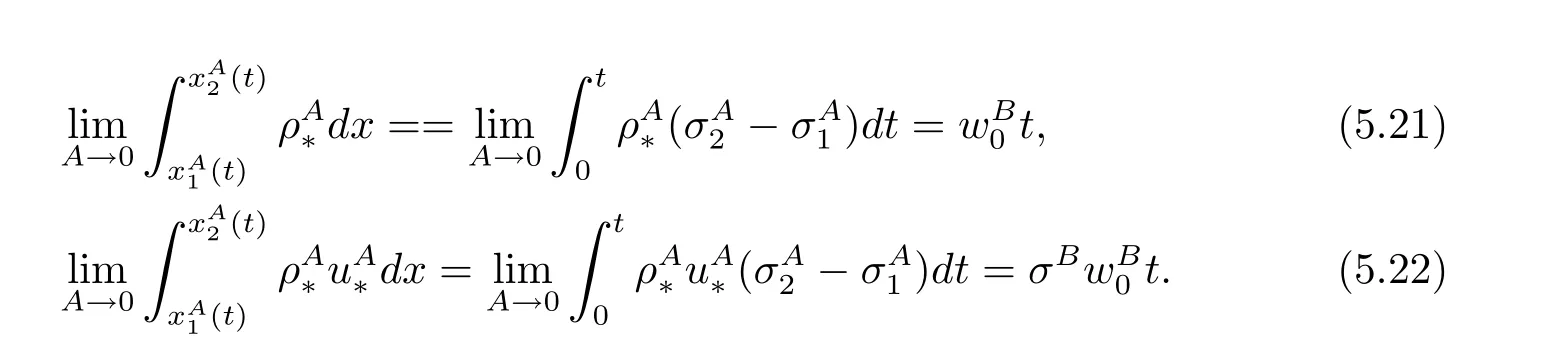
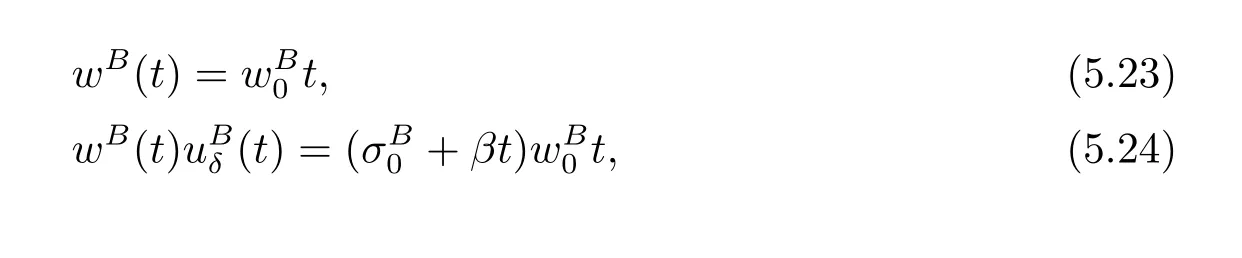


6 Conclusions and Discussions
杂志排行
数学杂志的其它文章
- ANALYTIC REGULARITY OF SOLUTIONS TO SPATIALLY HOMOGENEOUS LANDAU EQUATION
- GRADUAL HAUSDORFF METRIC AND ITS APPLICATIONS
- EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR CAPUTO-HADAMARD TYPE FRACTIONAL DIFFERENTIAL EQUATIONS
- ASYMPTOTIC BEHAVIOR OF COMPRESSIBLE NAVIER-STOKES FLUID IN POROUS MEDIUM
- 一类特殊矩阵的逆特征值问题
- 五次非线性Schrödinger 方程的一个新型守恒紧致差分格式
