,AnuarIshak,andIoanPop

Abstract: The present study considers the magnetohydrodynamic (MHD) stagnation point flow with chemical reaction effect over a permeable stretching/shrinking sheet. The partial differential equations are reduced to a set of ordinary differential equations using a similarity transformation. The transformed equations are then solved numerically by employing the bvp4c function available in the MATLAB software. The numerical results illustrate the effects of several parameters on the skin friction coefficient, local Nusselt number and the local Sherwood number. Dual solutions are obtained for a certain range of parameters. The temporal stability analysis is carried out to determine which one of these solutions is stable and thus physically reliable in a long run.

Keywords: Shrinking, dual solutions, stability, stagnation flow.

1 Introduction

In recent decades, studies pertaining to the boundary layer flow and heat transfer over a stretching or shrinking sheet have attracted considerable attention among the researchers due to its extensive applications in the industry which include the production of papers,fine-fiber mattes, roofing shingles, and insulting materials [Fisher (1967)]. In regard to this matter, it is also important to note the significance of the movements that occur in the fluid caused by the stretching/shrinking sheet which is parallel to it in order to control the drag and heat flux for the purpose of ensuring the best quality of the final product. The problem of the stretching sheet with movable velocity from the slit was first introduced by Crane [Crane (1970)]. Meanwhile, Miklavčič et al. [Miklavčič and Wang (2006)]were among the early researchers that investigated the flow over a shrinking sheet with the velocity moves towards the slit. Following this, the issue is becoming a common trend among the researchers which further emphasize the need to extend the problem of flow and heat transfer over a stretching/shrinking sheet to other different physical situations [Gupta and Gupta (1977); Bachok, Ishak and Pop (2010); Othman, Yacob,Bachok et al. (2017); Nasir, Ishak and Pop (2017); Merkin, Najib, Bachok et al. (2017);Jahan, Sakidin, Nazar et al. (2018); Kamal, Zaimi, Ishak et al. (2018)].

The study of magnetohydrodynamic (MHD) flow is still of current interest because of its wide application in the industry. The study of the incompressible viscous fluid in the presence of MHD effect was first conducted by Pavlov [Pavlov (1974)]. The application of strong external magnetic field is able to reduce the shrinking effect in the sheet [Lok,Ishak and Pop (2011)]. The rate of the heat transfer in the cooling process of the drawing strips can be controlled by the presence of the magnetic field in order to obtain an excellent quality of the final product [Chakrabarti and Gupta (1979)]. The experimental studies of MHD flow with various aspects were done by many researchers such as the study of unsteady MHD stagnation-point flow and heat transfer over a shrinking sheet done by Ismail et al. [Ismail, Arifin, Nazar et al. (2019)]. Further, the study of MHD flow in a micropolar fluid was done by Soid et al. [Soid, Ishak and Pop (2017)]. Both of these studies found that the existence of magnetic field expanded the domain of the solution.This finding was supported by Daniel et al. [Daniel, Aziz, Ismail et al. (2018)] through their study titled unsteady MHD nanofluid flow with thermal radiation. Jusoh et al.[Jusoh, Nazar and Pop (2018)] embarked on the investigation of MHD boundary layer flow and heat transfer of nanofluids with viscous dissipation effect. Instead of study the MHD flow over a flat sheet, there are some researchers who investigated the MHD flow past other type of geometries. Recently, Soid et al. [Soid, Ishak and Pop (2018)] had studied the MHD flow past a disk. Besides, Ibrahim et al. [Ibrahim and Tulu (2019)] had examined the MHD boundary layer flow past a wedge. The MHD stagnation point flow and heat transfer of a Jeffrey fluid with slip effects over a deformable surface was considered by Turkyilmazoglu [Turkyilmazoglu (2016)]. The analytical solutions for the mixed convection MHD fluid flow induced by a nonlinearly deforming permeable surface were reported by Turkyilmazoglu [Turkyilmazoglu (2018)]. The parameter domain for the existence of exact solutions was identified.

The scarcity in the study of fluid flow and heat transfer with chemical reaction has attracted the interest of the researchers to investigate the effects of chemical reaction in different physical aspects. A study by Bhattacharyya et al. [Bhattacharyya and Layek (2010)] was conducted to investigate the steady MHD flow and chemically reactive solution using quasi-linearization method. Following it, Bhattacharyya et al. [Bhattacharyya, Arif and Pramanik (2012)] extended this study to the shrinking sheet case. The study of the chemical reaction effects is very important in the industry, especially in an oxidation of solid materials and ceramics manufacturing. As reported by Mabood et al. [Mabood, Khan and Ismail (2015)], the flow field in the fluid flow can be affected by the appearance of the chemical reaction and magnetic field that appear on the stretching sheet.

The problem of MHD flow in a porous media with heat generation/absorption was investigated by Turkyilmazoglu [Turkyilmazoglu (2019)]. Sharma et al. [Sharma, Sinha,Yadav et al. (2018)] studied the effect of MHD mixed convective flow with heat generation/absorption using shooting technique. Furthermore, the MHD stagnation-point flow over the stretching/shrinking sheet in the presence of heat generation/absorption and chemical reaction effects was considered by Freidoonimehr et al. [Freidoonimehr, Rashidi and Jalilpour (2016)]. The present study aims to revisit the work of Freidoonimehr et al.[Freidoonimehr, Rashidi and Jalilpour (2016)] by emphasizing on the existence of dual solutions and their temporal stabilities that was not reported in that paper.

2 Basic equations

The current study considers a steady two-dimensional MHD stagnation point flow of an incompressible viscous and electrically conducting fluid that is driven by a permeable stretching/shrinking sheet. It is assumed that the velocity of the external flow is given by ue(x )= ax, while the velocity of the stretching/shrinking sheet is given by uw(x )=bx where a ( ＞0) and b are the constants subject to the stretching case b＞0 or the shrinking case b＜0 .

Meanwhile, the constant temperature and concentration at the surface are respectively denoted bywT and Cw, whereas the ambient (inviscid) temperature and concentration are respectively represented by T∞and C∞, with an assumption thatwT ＞T∞and Cw＞C∞.Apart from that, a uniform magnetic field of strength0B is applied in the positive direction of the y-axis. In addition, it is also assumed that the magnetic Reynolds number and the induced magnetic field are small and negligible.

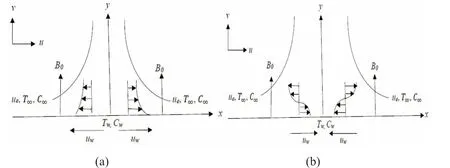
Figure 1: Physical model and coordinate system for (a) stretching and (b) shrinking sheet Under these assumptions, the governing equations can be written as [Freidoonimehr,Rashidi and Jalilpour (2016)]:

subjected to the following boundary conditions:

where ν is the kinematic viscosity, σ reflects the electrical conductivity, ρ represents the fluid density, T is the fluid temperature, k is the thermal conductivity of the fluid, cpis the specific heat capacity at constant pressure,0Q represents the volumetric rate of heat generation or absorption, C is the concentration, D is the diffusion coefficient, and R denotes the reaction rate of the solute.

The following set of similarity transformation is employed in order to solve Eqs. (1) to (4)along with the boundary conditions (5):

where η is the similarity variable, ψ represents the stream function defined as u =∂ψ /∂ y and ν =- ∂ψ /∂ x which identically satisfies Eq. (1). Eqs. (2)-(4) are respectively transformed to

which are subjected to the boundary conditions:

where λ represents the constant stretching/shrinking parameter, in which λ＞0 denotes the stretching, while λ ＜0 refers to the shrinking sheet. Moreover, M is the magnetic parameter, s indicates the constant mass flux parameter with s ＞0 corresponds to suction and s ＜0 is for injection. Meanwhile, Pr is the Prandtl number, ε ＞0 refers to the heat source and ε ＜0 is for the heat sink. Finally, Sc describes the Schmidt number and β denotes the reaction rate parameter, which are defined as:

The physical quantities of interest in the present study include the skin friction coefficient Cf, the local Nusselt number Nuxand the local Sherwood number Shxwhich can be expressed as

wherewτ is the surface shear stress, while qwand qmrespectively refer to the heat flux and the mass flux from the surface of the sheet which are respectively defined as:

On substitution of Eq. (6) into Eq. (13), one gets

where Rex= ue(x ) x /ν is the local Reynolds number.

3 Flow stability

The numerical results show the existence of dual solutions for Eqs. (7)-(10). Since two solutions are possible for a single value of parameter, the temporal stability analysis is necessary to be performed in order to determine the stability of the solutions in a long run.For this purpose, we introduce the unsteady case of Eqs. (1)-(5), and introduce the dimensionless time variables, τ, by following the pioneered work performed by Merkin[Merkin (1985)]. Similar approach was considered by Merrill et al. [Merrill, Beauchesne,Previte et al. (2006)]:

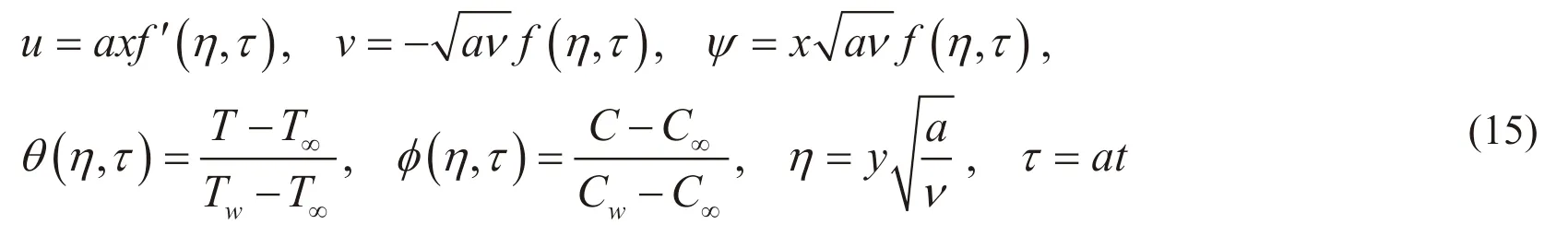
Eqs. (7)-(9) for the unsteady case can be written as

which are subjected to the following boundary conditions:

Following Weidman et al. [Weidman, Kubitschek and Davis (2006)], the basic flow solutionsandare perturbed in order to determine the temporal stability of the solutions:

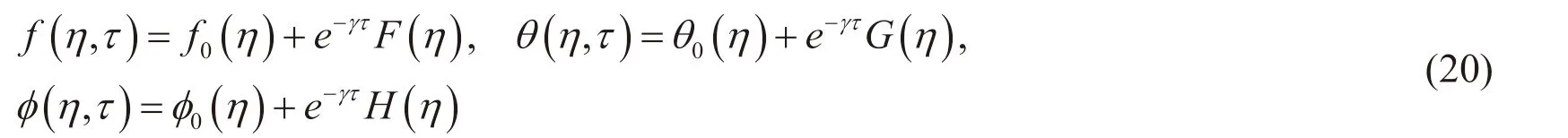
where γ represents the eigenvalue, while F ()η , G ()η , and H ()η are small relative tof0( )η, θ0( )η , and φ0( )η. The following system of linearized eigenvalue problems are obtained as a result of substituting Eq. (20) into Eqs. (16)-(18):

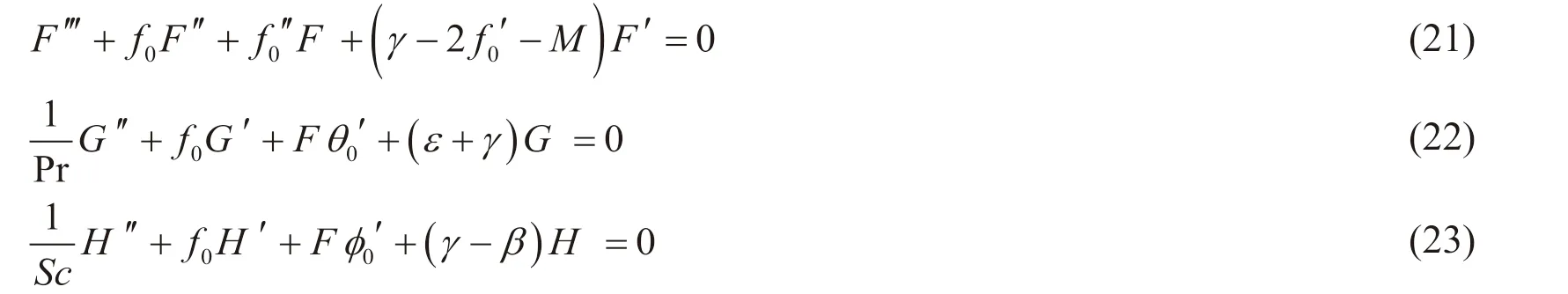
along with the boundary conditions

The temporal stability of the system is determined by the smallest eigenvalue,1γ.Following Harris et al. [Harris, Ingham and Pop (2009)] and Merrill et al. [Merrill,Beauchesne, Previte et al. (2006)], without loss of generality, we set F′′ (0) = 1 to obtain the values of1γ.

4 Results and discussion

The present study has comprehensively performed numerical computations for several values of magnetic parameter M, Prandtl number Pr, heat source/sink parameter ε,Schmidt number Sc, reaction rate parameter β, and suction parameter s on the velocity profiles, temperature profiles, concentration profiles, skin friction coefficient,local Nusselt number, and local Sherwood number. Eqs. (7)-(9) subject to the boundary conditions (10) were solved numerically using bvp4c function available in the MATLAB software as proposed by Shampine et al. [Shampine, Kierzenka and Reichelt (2000)]. In addition, all numerical computations are generated by setting the relative error tolerance of 10-7with the configured convergence criterion in order to achieve an accuracy up to six decimal places. The numerical results obtained in the current study are compared with the previously published results reported by Wang [Wang (2008)] and Jafar et al. [Jafar,Ishak and Nazar (2013)] for validation purposes as presented in Tab. 1, which shows a favorable agreement.

Table 1: Comparison of the skin friction coefficient, f'' (0)when M=s= 0 for several values of λ

Figs. 2-4 depict the variation of the skin friction coefficient f′(0) , the local Nusselt number -θ ′(0) and the local Sherwood number -φ ′(0) versus λ for various values of M,which are M = 0.3, 0.5, and 0.8 at constant values of Pr=1 , ε=0.5 , Sc=0.3 , β=0.4 ,and s=2 . As can be observed in those figures, dual solutions are possible when the sheet is shrunk, λ ＜0 , whereas the solution is unique when the sheet is stretched, λ ＞0 . Fig. 2 shows the increment in magnetic parameter that contributes to the increment of the skin friction coefficient f′(0) due to the interaction between magnetic field and the electrically conducting fluid that forms a drag-like force known as Lorentz force. It is important to note that this force produces the retardation effect that can increase the velocity gradient, thus allowing it to be applied in the electromagnetic coating of wires.

Figure 2: Variation of the skin friction coefficient, f"(0) versus λ for various values of M when s=2

Figure 3: Variation of the local Nusselt number -θ ′(0) versus λ for various values of M when Pr=1 , ε=0.5 , Sc=0.3 , β=0.4 and s=2

Figure 4: Variation of the local Sherwood number -φ'(0)versus λ for various values of M when Pr= 1, ε= 0.5, Sc= 0.3, β= 0.4 and s=2

Figs. 3 and 4 demonstrate the variations of the local Nusselt number -θ ′(0) and the local Sherwood number -φ ′(0) with λ for various values of M. As observed from these figures, two solutions are obtained for a certain range of the shrinking strength, λ ＜0 .On the other hand, the solution is unique for the stretching case, λ ＞0 . Solutions are possible up to λ = λc, which depends on M. These values of λcare given in Figs. 2 to 4.In Fig. 3, the range of λ for which the solution exists increases as the magnetic parameter M increases which results in the laminar flow retains longer before dispersing to the turbulent flow. Moreover, the positive Nusselt number in the figure shows that there is heat transfer from the surface of the fluid.

On the other hand, Fig. 5 shows that the velocity of the boundary layer thickness for the first solution is thinner compared to that of the second solution, which satisfies the far field boundary conditions asymptotically. Apart from that, Fig. 6 exhibits the concentration profiles for several values of Sc when Pr=1 , s=2 , ε=0.5 , β=0.4 ,λ=- 2.6, and M= 0.3. The finding reveals that the boundary layer thickness is reduced as the value of Schmidt number increases.

Figure 5: Velocity profiles f ′()η for several values of s when 2.6λ=- and M=0.3

Figure 6: Concentration profiles φ '(η ) for several values of Sc when Pr= 1,s= 2, ε= 0.5, β= 0.4, λ=- 2.6 and M=0.3

As previously discussed, dual solutions exist in this study for a certain range of the shrinking strength. In this regard, a temporal stability analysis is performed by solving the linearized eigenvalue problems Eqs. (21) to (24) in order to identify the stable solution. Referring to Fig. 7, the first solution is found to be stable and physically reliable,whereas the second solution is unstable as time passes, thus impractical in the real world applications for a long run. The stability of the solutions can be determined by finding the smallest eigenvalues γ, say1γ in (20). The positive smallest eigenvalues signify the presence of an initial decay of disturbance, thus indicating that the flow is stable. On the other hand, the negative smallest eigenvalue represents a growth of disturbance which causes the flow to be unstable in a long run.

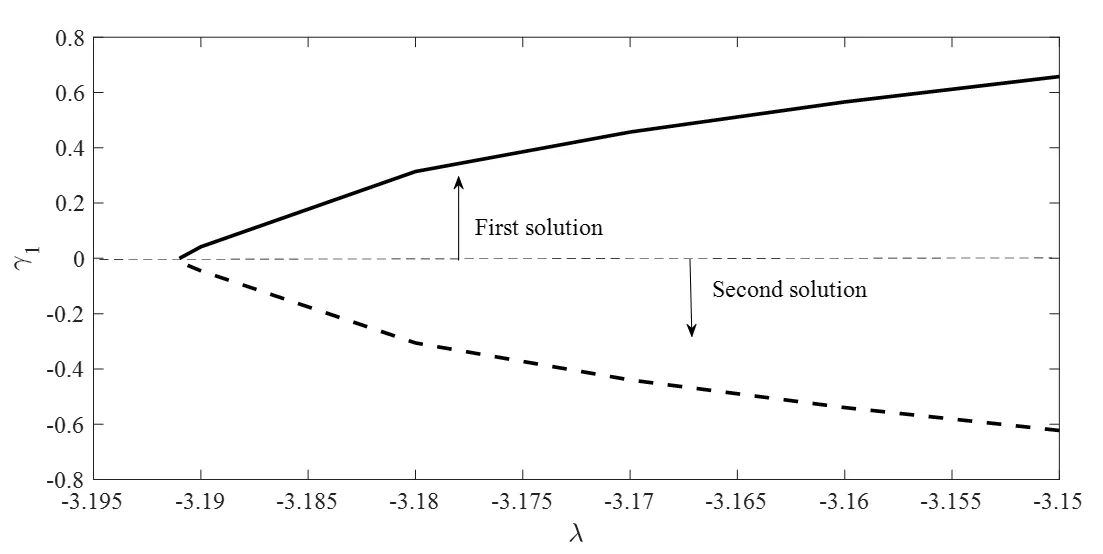
Figure 7: Plot of the lowest eigenvalues 1γ versus λ for s=2 and M =0.3

5 Conclusions

The present study considered the problem of MHD stagnation-point flow over a stretching/shrinking sheet in the presence of heat source/sink and chemical reaction effects. The governing nonlinear partial differential equations were reduced into a system of ordinary differential equations using a similarity transformation, which were then numerically solved by utilizing the bvp4c function in the MATLAB software. The effects of several parameters on the skin friction coefficient, local Nusselt number, and the local Sherwood number were also discussed. More importantly, the findings revealed that the increment of magnetic parameter and suction tended to result in the increment of the skin friction coefficient. However, the opposite trend occurred on the local Nusselt number and the local Sherwood number. In addition, it is worth to note that dual solutions were found to exist for a certain range of the shrinking strength. The temporal stability analysis revealed that only one of the solutions is stable and thus physically reliable in a long run.

Acknowledgement:The financial support received from the Universiti Kebangsaan Malaysia (Project Code: GUP-2018-153) is gratefully acknowledged.