房立超，王 钰，杨杏丽，李济洪

1.山西大学 数学科学学院，太原 030006

2.山西大学 现代教育技术学院，太原 030006

3.山西大学 软件学院，太原 030006

1 引言

所谓机器学习就是基于数据来建立合适的模型，并运用建立的模型对新数据进行预测与分析，其主要目的是获取具有较好泛化能力的模型，因此模型选择在机器学习中显得尤为重要。在进行模型选择时为了防止模型发生过拟合的现象，学者们通常使用正则化的思想来解决，即在损失函数中加入惩罚项，也就是说，假设J(θ)为刻画模型在训练集上的表现的损失函数，那么在进行模型选择时不是用J(θ)来评价，而是以J(θ)+λR(θ)的好坏来选择模型，其中R(θ)用来描述对参数θ的惩罚，λ>0 为调节参数，λ越大表示对参数θ的惩罚越大。20世纪以来，大量讨论模型选择准则的文献相继问世，并以1973年日本学者Akaike[1]提出的著名的AIC信息准则（Akaike information criterion）为标志，从此拉开模型选择研究的序幕，随后Schwarz[2]于1978年提出与AIC准则相似的贝叶斯信息准则（Bayesian information criterion，BIC）。AIC和BIC都在目标式中引入了关于模型参数个数的惩罚项，且这两种经典的基于正则化的模型选择准则一直沿用至今；1996年Tibshirani提出了经典的LASSO（least absolute shrinkage and selection operator）算法[3]，此算法可以同时实现参数估计和显著性变量的选择，随后由此方法衍生出了grouped LASSO、adaptive LASSO和SCAD（smoothly clipped absolute deviation）等算法[4-6]；Hwang 等[7]基于 MSC（multi-class signomial classification）思想，提出了L1范数正则化函数和基于此函数进行多分类问题变量选择的方法，对于具有大量变量的数据集，所提出的方法减少了变量的数量，同时提高了分类准确性；另外Wang等提出了组块3×2交叉验证t检验[8]方法，并通过实验验证了其在低维数据上模型对照方面的优良性质；Reenen等[9]使用最小分类错误率作为检验统计量，通过非参数假设检验找到统计上显著变化的变量，作为最终模型中入选的变量；Lever等[10]讨论了模型选择的过拟合问题，认为在一个数据集上得到具有适当复杂性的模型需要在偏差和方差之间找到平衡点，并通过实验证明了交叉验证方法可以帮助避免过拟合的发生并生成一个能够很好地处理新数据的模型。

本研究主要关注分类情形的模型选择问题，即对于给定的某个数据集，基于某个性能度量指标构造模型选择准则，并基于此准则选出多个分类器（算法）中性能最好的一个。其中，泛化误差是最常用的性能度量指标之一，而理论的泛化误差度量由于其分布的复杂性或未知性往往无法得到，实际中常基于它的估计来进行模型的选择。关于泛化误差的估计文献中提出了很多的方法，如广泛使用的交叉验证估计方法，包括留一交叉验证（leave one out crossvalidation，LOOCV）、留P交叉验证、K折交叉验证、RLT交叉验证（repeated learning-test cross-validation）、蒙特卡洛交叉验证、5×2交叉验证、组块3×2交叉验证（block 3×2 cross-validation）等[11-21]。

然而注意到，基于泛化误差估计的方法在选择模型过程中只使用了估计本身（均值的信息）而没有考虑估计的方差的信息，较大的方差会使得该性能指标产生较大的波动，有可能选择较复杂的模型作为最优模型，导致该模型的泛化性能较差，如图1（文献[22]）所示。另外，对于上述提到的交叉验证估计，Arlot和Celisse[23]也通过实验验证了当这些估计方法的偏差相同时，它们的表现却可以截然不同，实际上这是由这些估计的方差差异导致，即估计的方差对模型选择有很大的影响。于是，在进行模型选择时不仅需要考虑性能度量的估计本身，还要考虑它的方差。如果能在上述性能度量指标下提出融合方差信息的模型选择准则或方法，将为模型选择相关研究提供新的思路与方法。

Fig.1 Effect of bias and variance on total error and model complexity图1 偏差与方差对总误差和模型复杂度的影响

综上所述，由于估计的方差对模型选择有较大的影响，借鉴了线性模型中加入参数惩罚项的正则化思想，在求泛化误差估计最小化的同时加入一个正则化项，该正则化项用来表示对泛化误差估计的方差的惩罚，求取使得泛化误差估计和该估计的方差惩罚项同时达到最小时的模型作为最终的模型选择结果。即本研究所使用的模型选择准则由“泛化误差估计+泛化误差估计的方差的惩罚项”组成。在线性模型中的变量选择准则和这里的模型选择准则有异曲同工之处，如传统使用的AIC准则为“-log似然+模型参数个数的惩罚”，“-log似然”可以看成是对模型拟合度的评价，即和泛化误差的估计的作用相同；另外，由于在线性模型中模型的参数个数与参数估计的方差存在正比例关系，线性模型中包含的参数个数越多，该模型的参数估计的方差越大，于是AIC准则中的“模型参数个数的惩罚”和“泛化误差估计的方差惩罚项”起着相同的作用。本文把加入泛化误差估计的方差正则化的思想引入到了分类模型选择的问题中，构造了一个可以广泛使用的方差正则化分类模型选择准则。

2 方差正则化的分类模型选择准则

2.1 基于泛化误差的组块3×2交叉验证估计的模型选择

在机器学习中，泛化误差是用于模型选择的通用性能度量指标，它指的是所选模型在独立测试样本上的期望预测误差。具体地，如果令数据集，其中 xi是输入变量，yi是输出变量，f(x)为预测模型，为0-1损失函数，则泛化误差可表示为如下形式：

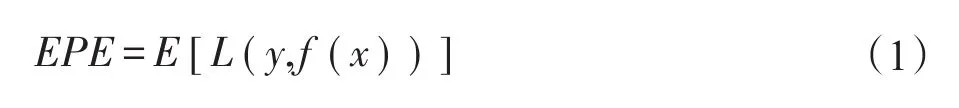
由式（1）可知，泛化误差的计算依赖于数据的分布，然而现实中数据的分布往往无法获得或者数据的分布非常复杂，因此理论泛化误差的计算非常困难，以至于直接基于它进行算法性能的评价更无从谈起，于是现实中常常基于泛化误差的估计进行模型的选择。

鉴于文献[20-21]中提出的泛化误差的组块3×2交叉验证估计方法的优良性能，本研究中考虑使用此交叉验证法来估计泛化误差。具体地，组块3×2交叉验证方法是将数据集Dn划分为大小相等且互不相交的4个子集Pj,j=1,2,3,4，然后任取其中两个子集作为训练集，剩余两子集作为测试集，做一次2折交叉验证，于是根据不同的组合总共可以得到3次2折交叉验证的预测误差估计（具体数据划分见表1），那么基于3组估计结果进行平均的泛化误差的组块3×2交叉验证估计可表示为如下形式：

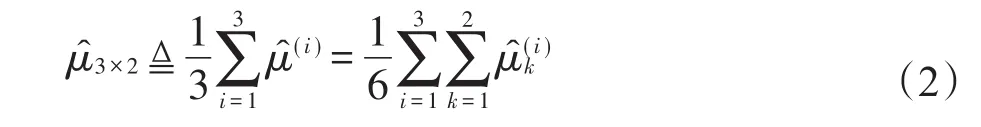
Table 1 Data partitions of block 3×2 cross-validation表1 组块3×2交叉验证的数据切分

其中，M为候选模型集。

2.2 方差正则化的分类模型选择准则

在提出方差正则化的分类模型选择准则之前，先给出组块3×2交叉验证泛化误差估计的方差以及该方差的估计。该泛化误差估计的方差和方差的估计已在文献[8]中有详细描述，这里给出其简要过程。

引理1[17]令U1,U2,…,Uk为随机变量，且具有公共的均值β，方差δ=Var[Uk],∀k和协方差,分别表示样本方差和样本均值，则有：

于是发现该真实方差由方差、组内协方差和组间协方差三部分组成。因此如果直接使用传统的样本方差进行方差估计将导致激进的结果。故文献[8]将组内和组间的协方差同时考虑到方差估计中后，得出了的一个较为保守的估计形式：

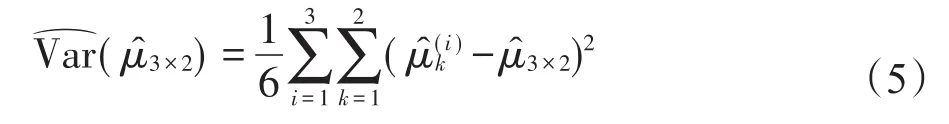
后面将使用式（5）作为泛化误差的组块3×2交叉验证估计的方差估计。

在式（3）定义的模型选择准则中，它只考虑了基于泛化误差估计本身来进行模型的选择，没有考虑估计的好坏（方差），这显然是不合适的，因为较大的方差使得泛化误差的性能波动较大，可能选择到较复杂的模型，从而导致较低的泛化性（见图1）。为此，构造了一种添加方差正则化项的新的模型选择方法（准则），即在式（3）的基础上，将泛化误差估计的方差估计加入，准则形式如下：

2.3 评价指标

本节给出接下来的实验部分评价不同模型选择准则性能时所使用的指标。本文关注于分类问题下的最优分类器选择问题，即在相同数据设置下，根据不同的模型选择准则，在所给分类器中选出各准则对应的最优分类器。由于数据的随机性，把实验重复N次（第3章实验中N=1 000），观察给定的每个分类器作为最优分类器被选中的次数。N次实验中选中次数最多的分类器可以认为是更符合该数据集的分类器，记该分类器为目标分类器，不同的模型选择准则的评价标准，就以选中目标分类器的次数作为评价指标，选中A的次数越多说明该准则越好。

3 模拟实验

本章首先通过模拟实验验证了文献[8]中提出的方差估计的合理性，然后分别在两个模拟数据和3个真实数据上（Letter数据集、MAGIC Gamma Telescope数据集和Abalone数据集[24]）验证了提出的新的分类模型选择准则相对于传统模型选择方法的优越性。

3.1 方差估计

对于泛化误差的组块3×2交叉验证估计的方差，需要验证式（5）是否可以作为它的一个合理估计，考虑一个二分类问题，数据集Z=(X,Y)，其中X为预测变量，Y为类别响应变量，且满足P(Y=0)=P(Y=1)=0.5，X|Y=0～N(05,I5)，X|Y=1～N(15,2I5)，05和15分别表示元素全部为0和1的5维向量，I5表示5阶单位矩阵，总样本量n=200。在此数据集上，给出了6个分类器（见表2）的真实方差，由式（5）得到的方差估计和一般意义上的样本方差。

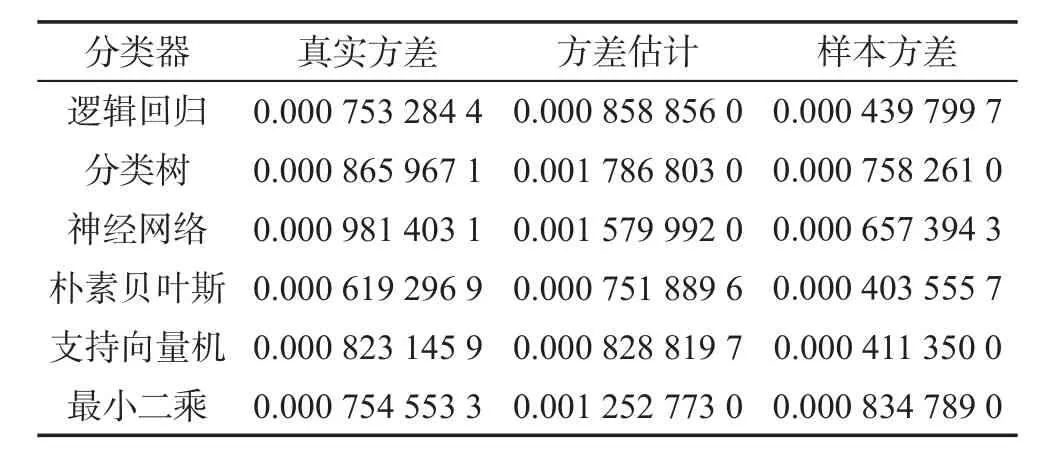
Table 2 Results of variance simulations表2 方差模拟结果

观察表2可以看出，6个分类器中只有在使用最小二乘作为分类器时得到的样本方差估计大于真实方差（这可能是由于最小二乘方法从严格意义上来说并不是一个真正的分类器），其他分类器上均低估了真实方差，有的分类器低估的程度还比较严重，如支持向量机的真实方差为0.000 823 145 9，而样本方差仅为0.000 411 350 0，只有真实方差的一半，严重低估了真实方差，这说明用样本方差来估计真实方差是激进的；另一方面，比较真实方差和式（5）得到的方差估计两列，可以看出方差估计均大于真实方差，即式（5）得到的方差估计是真实方差的保守估计，于是在基于方差正则化准则式（6）做模型选择时使用此方差估计较之样本方差更保守，得到的模型选择结果更值得信赖。因此，在下面的实验中，采用式（5）的方差估计进行模型选择。

3.2 模型选择准则性能对照

为了体现方差正则化模型选择准则的性能，在二分类的两个模拟数据和两个真实数据上分别给出传统的泛化误差估计准则和方差正则化准则的模型选择结果。先考虑了两种方差正则化项的具体形式，见下面的准则2和准则3，准则1即为传统的基于泛化误差估计的准则。

3.2.1 实验设置

数据1（模拟数据）数据集Z=(X,Y)，X～N(15,2I5)，ln(Y/(1-Y))=Xβ+ε，其中 β=(15)T，ε～N(0,2)，总样本量n=200。用于模型选择的分类算法为神经网络、朴素贝叶斯和支持向量机（support vector machine，SVM）。

数据2（模拟数据）数据集Z=(X,Y)，总样本量n为100，其中Y=1的样本个数为40，Y=0的样本个数为 60，且Xi|Y=1～N(0,1)，X1|Y=0～N(0.4,1)，X2|Y=0～N(0.3,1)，X3|Y=0～N(0,1)，Xi之间相互独立，i=1，2，3。用于模型选择的分类算法为分类树、神经网络、朴素贝叶斯和SVM。

数据3（真实数据）UCI数据库的Letter数据集[24]，自变量16个，原始样本量为20 000，是一个多分类问题。为构造一个二分类问题，将类别标签为A～M的看成第一类，N～Z的看成第二类，随机抽取样本量n=200的样本作为实验数据集。选择分类树、神经网络和SVM作为分类算法。

数据4（真实数据）来自UCI数据库的MAGIC Gamma Telescope数据集[24]（大气切伦科夫望远镜项目伽马成像数据集），特征变量10个，总的样本量19 020，为二分类数据集。从中随机抽取样本量n=200的样本为实验数据，分类算法选择神经网络、朴素贝叶斯和SVM。

3.2.2 实验结果及分析

根据数据1设置，随机生成1 000组数据，针对每一组数据，根据3.2节给出的3个准则，在给出的分类器中分别选出使得性能度量指标最小的分类器，最后统计出在1 000次结果中每个分类器在每个准则下被选中的次数。同理在数据2～数据4上进行实验。3个准则的实验结果见表3。

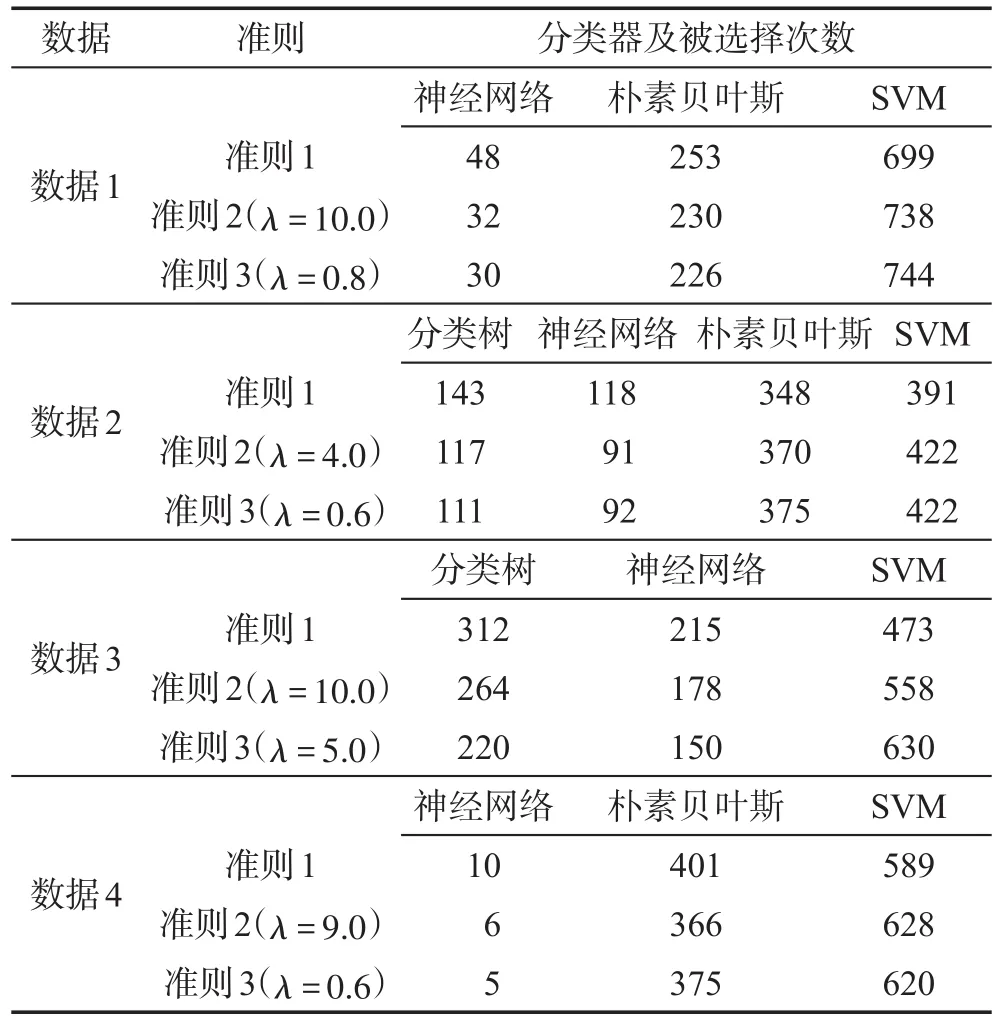
Table 3 Comparison of results of model selection simulations on data sets 1～4表3 数据1～4模型选择模拟结果的比较

由表3可以看出在数据1上，3个准则选中的目标分类器均是SVM，准则1共选中699次，准则2在λ=10.0时选中目标分类器的次数相比准则1增加了5.58%，准则3（λ=0.8）选中SVM的次数有744次，此时比准则1高出6.44%。数据2的表现与数据1类似，准则1选中的目标分类器为SVM（391次），准则2（λ=4.0时）和准则3（λ=0.6时）在1 000次模拟中选中SVM的次数均为422，比准则1高出7.93%。与前两个模拟数据相比，在真实数据3上本文的新准则相比传统准则表现得更突出，传统准则选中目标分类器SVM的次数为473，而准则3（λ=5.0时）选中SVM次数为630，比准则1高出了33.19%。同时，在真实数据4上也可观察得出以上类似的结论，与准则1选中目标分类器SVM的次数为589相比，准则2（λ=9.0时）选中SVM的次数最高为628，高出了6.62%。

另一方面，对比了每一组数据下的分类器所产生的泛化误差的方差大小之间的差异，结果见表4，在数据1的1 000次模拟中，每一次将3个分类器产生的泛化误差的方差中相比最小的选出，则3个分类器下泛化误差的方差最小的次数分别有190、322和488，而此时本文的目标分类器就是次数最多的SVM；同样在数据2～4上，SVM产生的泛化误差的方差小于其他分类器产生的泛化误差的方差的次数均最多。发现，在数据3上希望被选择的目标分类器的泛化误差的方差小于其他分类器的次数是最多的，而此时使用本文构造的新准则能够很大程度地提高选中该目标分类器的次数，也就是说，因为此时目标分类器产生的泛化误差的方差更小，所以使用新准则提高了模型选中该分类器的概率，然而如果忽略方差信息，即仅根据泛化误差进行判别，就可能导致选中并不合适的分类器或者说降低了目标分类器被选的概率。

3.3 调节参数对模型选择结果的影响

Table 4 Comparison of variances of generalization errors表4 泛化误差的方差的比较

在本文所提出的方差正则化分类模型选择准则式（6）的框架下，最优模型的选择可以通过最小化的值来获得，但是其中的调节参数λ是未知的，且λ的不同取值也会产生不同的结果，因此参数λ的选取同样重要。本节给出前面四组数据在准则2和准则3上随λ变化的结果，这里λ取值为从0到10，且λ=0时所对应的就是准则1的情况，即仅仅依据泛化误差的组块3×2交叉验证估计来进行模型选择的一般准则。结果见表5和表6。

Table 5 Results of model selection simulations of criterion 2 with change of λ表5 准则2随λ变化的模型选择模拟结果

Table 6 Results of model selection simulations of criterion 3 with change of λ表6 准则3随λ变化的模型选择模拟结果

可以看出，加入方差正则化项之后的模型选择准则在使用方差估计（准则2）作为正则化项时，比传统的模型选择准则有更好的稳定性；而加入标准差估计（准则3）为正则化项的模型选择准则，选择到目标分类的次数随着λ的增加一开始上升随后下降，但总体说来只要调节参数λ取得合适，加入标准差估计的正则化模型选择准则性能更有优势；从表中还可以看到，不同的调节参数对模型选择的结果影响很大，这说明，同线性模型变量选择方法相似，方差正则化的模型选择研究中，调节参数的选择也是一个不可避免的问题，在进一步的工作中，应考虑使用什么具体的策略来选择调节参数更合适（如通常使用的交叉验证类的调节参数选择方法）。

3.4 方差正则化函数的选择

在前边提出的方差正则化的分类模型选择准则中，关于泛化误差估计的方差估计的函数同样需要预先确定，一般认为该惩罚函数是方差的增函数即可，但函数的具体形式在不同的数据集上性能是不同的。如对比表5和表6的结果，准则3比准则2更快地达到模型选择的最优，这可能和这些分类器自身的方差大小有关系（见表2），这些分类器的方差都远小于1，开根号之后的标准差估计使得对于相同的调节参数值，在模型选择时更侧重于正则化项，从而可以很快达到最好的模型选择性能。这从一个侧面反映，针对具体的实际问题，正则化项函数的具体形式（如线性函数、指数函数）需要进行慎重选择。本节给出方差正则化项的函数为方差估计的指数函数时的实验结果和分析。

以3.2节中的数据2和数据4为例，实验设置及实验过程同前，方差的指数函数作为惩罚项时的准则的模型选择模拟结果见表7，两个数据下选择的最优分类器与3.2节中一致，且以关于方差估计的指数函数作为正则化项的准则依旧能够提高目标分类器被选中的次数，说明此准则同样有效。

3.5 多分类数据上模型选择准则的性能

前述实验结果均是在二分类数据集上得来的，本节将模型选择准则应用到多分类数据集进行模拟实验，以验证在多分类数据集上本文方法的效果。

3.5.1 实验设置

数据5（真实数据）来自UCI数据库的Avila数据集[24]，为多分类数据集。此数据集是从“Avila圣经”的800张图片中提取的拉丁文数据，经分析由12名抄写员完成，总样本量20 867，特征变量10个，输出结果为12个抄写员之一。从中随机抽取样本量n=200的样本进行实验，分类算法选择神经网络、朴素贝叶斯、最小二乘和K近邻（K=5）算法。

Table 7 Simulation results of criterion with exponential function of variance as penalty表7 方差的指数函数作为惩罚项的准则模拟结果

3.5.2 实验结果及分析

同3.2节的实验过程相似，从数据5中随机生成N（N=1 000）组样本量为200的数据集，在每一个数据集上，根据3.2节的3个准则选出最优分类器，最终结果为1 000次模拟中每个分类器在各个准则下被选中的次数。结果见表8。

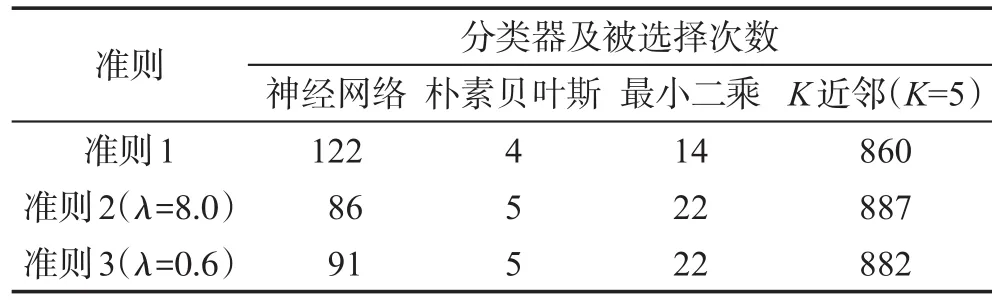
Table 8 Results of model selection simulations on data 5表8 数据5模型选择模拟结果

与前面4个数据不同，数据5是一个多分类数据，在此数据集上，当抽取的样本量为n=200时，根据3个准则选出的最优分类器均是K近邻（K=5）（分别选中860、887、882次），且准则2和准则3相比准则1选中目标分类器的次数均有所提高，也就是说，方差正则化的分类模型选择准则在多分类数据上依然有效。

另外，该节的实验结果都是在数据集的样本量有限时所做的实验（n=200，实际中所能得到的数据集总是有限样本），当样本量无限增大时，加入方差正则化项的模型选择的性能如何，样本量有限时得到的结论在样本量增加时是否成立，这一问题仍待解决，将在下一章讨论。

4 方差正则化的分类模型选择准则理论性质

上一章的实验验证了在有限的样本量下，方差正则化的分类模型选择准则能更稳定地选择较优的模型，接下来将在理论上进一步说明此模型选择方法在样本量趋于无穷时同样能够选择到该较优的模型，即具有模型选择的保序性。下面先给出一些记号。

数据集Z=(X,Y)且样本之间独立同分布，样本量为n，X为自变量，Y为类别变量，取值为0或1，记第i个测试样本的真值为yi。两个分类器为δA和δB，第i个测试样本在 δA和 δB上的预测值分别为。在0-1损失下，两个分类器的测试误差为和表示 δB分错的概率与δA分错的概率之差，，其中表示两个分类器的预测值不一致的概率。两个分类器的泛化误差的组块3×2交叉验证估计记为它们的方差估计为下面先给出文献[25]中的结论作为理论证明的基础。

引理2[25]对有限的样本量n，如果基于组块3×2交叉验证泛化误差的模型选择方法判别出分类器δA的性能优于分类器δB，那么随着样本量的增加，此结论仍然成立。即当n→∞，nΔRn→∞时，成立。

定理1在有限的样本量n下，如果基于组块3×2交叉验证的加入方差估计正则化项的模型选择方法判别出分类器δA的性能优于分类器δB，那么随着样本量的增加，此结论仍然成立。具体地，当n→∞，nΔRn→∞ 时 ，成立。

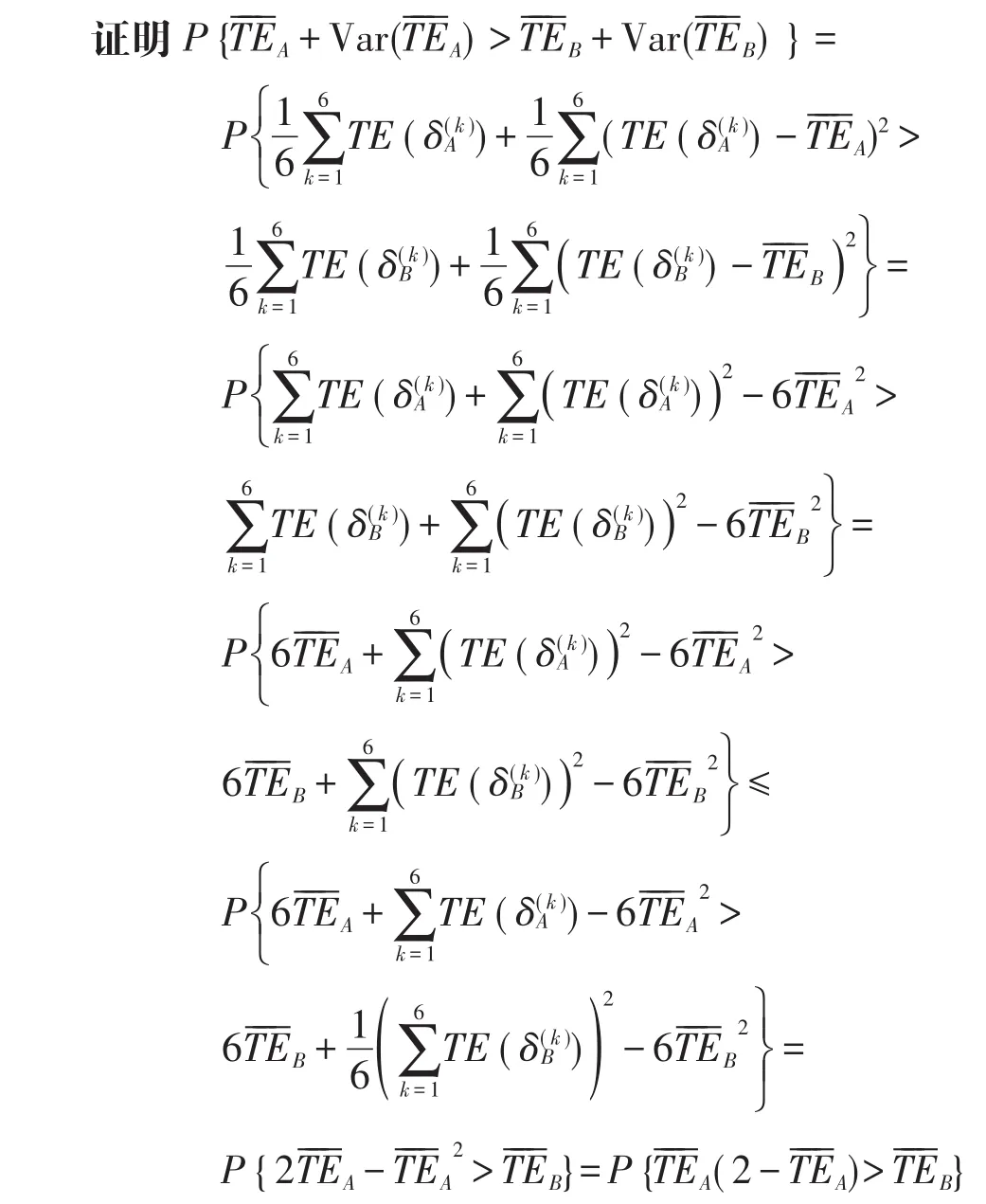
5 结束语

模型的泛化性能是机器学习中度量一个模型优劣的最重要指标，传统的模型选择方法或者只对比模型的泛化误差估计，或者使用统计显著性检验引入泛化误差估计的方差信息，但由于具有较小的泛化误差估计的模型往往方差较大，统计显著性检验依赖于数据的分布假设（这一假设往往不成立），且对多个模型两两进行对照检验时计算复杂度很大，基于此，将泛化误差的方差估计添加到模型选择准则中，构造了一种基于泛化误差的组块3×2交叉验证估计的方差正则化的模型选择准则，并通过实验验证了在模拟和真实数据上，所提方法相比传统的只包含泛化误差信息的模型选择方法具有更好的性能。进一步，在理论上证明了考虑方差估计之后的模型选择准则，有限样本上得到的结论在样本量趋于无穷时同样成立。

同时，应看到加入方差正则化项的模型选择准则虽然在一定程度上缓解了传统模型选择准则选择到较差模型的概率，但是并没有使得选择到较差模型的概率降到0；另外，本文提出的新准则在具体实现时，需要给出正则化惩罚项函数的具体形式，对实际问题而言，这是个重要的研究问题；最后，与传统的以泛化误差估计作为模型选择度量指标的准则相比，新准则引入了一个调节参数λ，不同的调节参数的模型选择结果是不同的，势必就要考虑新准则的调节参数选择问题。将来的研究中，将在更多的数据和分类器上进一步测试所提方法的性能，并试图分析加入方差正则化项的模型选择准则的调节参数选择方法和正则化项的函数形式。