一种四边形网格上的Midedge细分格式
2019-04-15檀结庆曹宁宁
檀结庆 ,曹宁宁
(1.合肥工业大学数学学院,安徽合肥230601;2.合肥工业大学计算机学院,安徽合肥230601)
0 引 言
曲面细分就是通过对给定控制网格M的迭代计算,不断加细原有网格,或保留原有控制顶点(插值型),或去除原有控制顶点(非插值型),生成一系列不断加细的网格M1,M2,…,Mn,…,最终收敛到极限M∞。曲面细分由于格式简单,只涉及局部计算,被广泛应用于具有良好流线型性质的曲面设计、游戏、视频场景的快速重建等几何造型领域,以及医学图像的多分辨率分析,通过细分可得到医学图像的分层细节。
每一步细分过程都可分成两部分:拓扑上的分离,决定每一步控制网格的变化(连线规则);几何上的规则,决定新网格点的计算方式。
由此看来,新的细分格式至少可通过2种方法得到:改变其拓扑规则或几何规则。改变拓扑规则比较著名的细分格式主要有:四边形网格细分中由CATMULL等[1]提出的分离因子为1-4的CC格式,PETERS等[2]提出的因子为 1-2的Midedge格式,LI等[3]提出的因子为1-2的格式;三角形网格中有LOOP[4]提出的因子为1-4的loop格式,KOBBELT[5]提出的因子为1-3的格式,VELHO 等[6]提出的4-8格式;此外,六边形网格的细分格式中还有CLAES等[7]的 1-3切角细分格式,和郑立垠等[8]提出的1-4砍边格式。在细分的几何规则方面:通过探求不同基函数,如拉格朗日函数、B样条函数的性质,得到不同细分掩模的格式,而曲面细分控制顶点的空间分布多样性,则可通过改变细分模板得到许多不同的曲面细分格式。如KOBBELT[9]提出的加参数后的四边形网格细分格式,可视为对CC格式模板的改变;DYN等[10]提出的分离因子为1-4的Butterfly格式,即为对Loop格式模板的更改。
本文基于分离因子为1-2的Midedge细分格式的拓扑规则,使用新的几何规则对四边形的每一条边插入中点,并依次相连,然后去除原先的点,如此构成新的四边形网格。
1 细分格式的来源
要想得到新的细分格式,只能从改变细分的拓扑规则或几何规则入手。新的细分规则既要保证网格加细前后的拓扑结构不变,又要保证所选模板的对称性和唯一性。对称性,是指模板中的点相对于要插入的点具有相同的位置关系,其掩模相同;唯一性,是指细分规则设定好后,插入的新点的计算结果唯一。

图1 四边形网格细分的拓扑规则Fig.1 Topological rules for subdivision of quadrilateral meshes
图1为现有的一些细分格式的拓扑规则。本文将新的细分格式的构造转到对几何规则的改变上,即构造一种全新的插入点的计算方式。通过对比三角形细分格式中的 Loop格式[4]和 Butterfly格式[10](见图2)易发现,同为三角形网格细分的中点格式,其主要区别为生成新点的模板不同。相应的细分掩模(仅列出插值型)为:
(1)Loop格式掩模:

(2)Butterfly格式掩模:


模板选取时首先要满足对称性。三角形网格在3个方向上均对称,因此,在Loop格式模板上修改时也必须满足3个方向对称。Butterfly格式即为对Loop格式模板的扩张。在Loop模板的基础上,以新加入的点P为中心,向P→P1P4,P→P4P2,P→P2P3和P→P3P1方向扩张一步,得到Butterfly格式的模板,仍保持原模板关于新加入点的三方向的对称性。
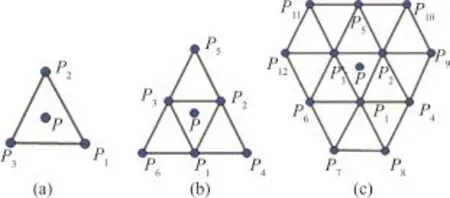
图3细分格式Fig.3subdivision scheme
改变一个细分的模板,就能得到计算新顶点的新几何规则,进而得到新的细分格式。基于分离因子为1-2的最简单的Midedge细分:由一条边上的2个点进行加权平均,得到这条边的中点。对四边形网格的4条边采用同样的方式得到相应的4个边点,依次相连,舍弃原来的点和边,完成1次细分。DOO等[14]还发现,连续2次细分后,就成为DOOSABIN格式。
从图4可以看出,Midedge格式的模板就是一条线段,用线段两端点的信息生成1个中点。本文将对这一简单模板进行推广。因四边形网格为二方向网格(也有人称四方向网格),Midedge以边为基本单位生成新的点,按网格方向对其模板进一步扩充,只能将其延伸成类似Loop格式的模板,即如图5(a)所示的模板,由6个点生成1个点。 此模板仍具对称性,且已有网格中每条边生成的点是唯一的。本文采用图5(a)所示的模板,虽然可对此模板进行扩充,但由这20个点生成1个边点,有些浪费和烦琐了,与实际应用所要求的简单快捷不符,不再继续讨论。
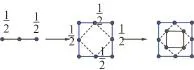
图4 Midedge细分Fig.4 Midedge subdivision scheme
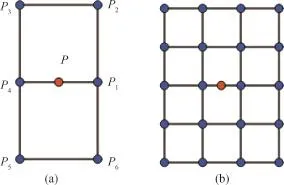
图5 对Midedge格式模板的扩充Fig.5 Stencil extension of Midedge subdivision scheme
2 新的Midedge格式
本节,将以图5(a)所示的新的模板为基准,确定新的细分格式的掩模。
由图5(a)知,细分掩模要满足对称性,则生成新的边点的掩模应具有以下形式:
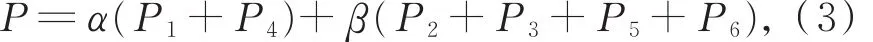
其中,2α+4β=1。
由于模板的对称性,可将其中一个方向(这里显然是横向的)上的值看作1个定值,则可将问题转化为 3 点问题,即可将P1与P4,P5与P6,P2与P3分别看作1个点,这样原来的曲面细分为由3个点生成1个中间点的问题。本文采用三点二重的逼近型细分格式[15]来解决此问题。三点二重细分格式的形式如下:

其中,a1+a2+a3=1。
若令a1=m,a2=1-m-n,a3=n,则此三点二重格式的细分掩模为
[…,0,m,n,1-m-n,1-m-n,n,m,0,… ],可通过曲线细分的生成多项式的相关充分条件[16]求得,也可通过4次B样条生成多项式直接得到于是可得即三点二重格式的细分掩模为

插入点的位置如图6所示。

图6 三点二重曲线细分格式的插入点位置Fig.6 Position of the insertion point of three point binary curve subdivision
回顾之前的目标,是为了用3个点生成1个新的中间点,于是,令

综上所述,有

于是,确定此细分格式的掩模,新的Midedge格式的几何规则为

2步的Midedge格式就是一种Doo-Sabin格式。因此,将本文提出的新的Midedge格式应用于2步,便是如图7所示模板的细分。由图7知,2步Midedge格式可以生成P点,但空心点P14,P41,P44对生成P点并未做贡献;其他3个点可用同样的方式计算。P的细分掩模如下:
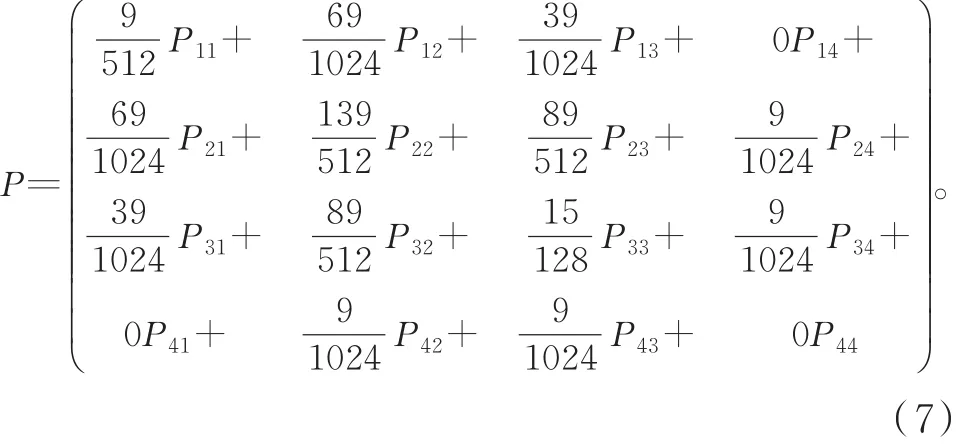

图7 2步的Midedge格式Fig.7 Two-step-Midedge subdivision scheme
3 细分的连续性
定理[17]设细分矩阵S是一个n×n矩阵,λ1,λ2, …,λn是 矩 阵S从 大 到 小 排 列 的 特 征 值 ,v1,v2, …,vn分别是对应于特征值的特征向量,若满足:
(1)1=λ1>λ2=λ3>λ4,并且λ2的几何重数与代数重数都是2;
(2)矩阵S对应于v2,v3的特征映射

是单射且正则的(det(∂ψ(u,v,j)/∂(u,v))≠ 0)。其中Ω是J个单位正方形在一定拓扑结构下构成的参 数 空 间 ,j∈ (1,J),u,v∈ (0,1),b(u,v,j)是 一个以方程为元素的n维行向量,满足其 中bk(u,v,j)∈C1(Ω) 是b(u,v,j)的第k个元素。则细分矩阵S对应的细分格式的极限曲面是正则的,即C1连续。
细分矩阵的确定:首先要选取合适的初始控制网格M0,在给出的掩模矩阵S下,进行细分,生成新的有着同样拓扑的控制网格M1,如此往复,构成迭代形式:

其中i为正整数。
从图7中可以看出,由于单一Midedge格式拓扑规则的特殊性,一个标准的n×n网格无法生成标准的m×m网格。于是,用2步Midedge格式,计算细分矩阵S2。若S2的特征值已知,由矩阵的性质易得S的特征值(前者特征值是后者的平方)。
2步Midedge格式,要想选取的模板在细分矩阵S2加细下循环迭代,须选取6×6的网格点。因此,2步Midedge格式的细分矩阵S2应该是36×36的。参照图8,给出细分矩阵S2的形式:

其中
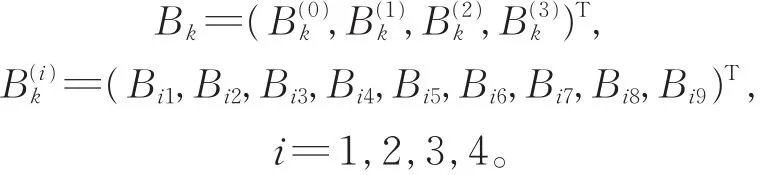
则S2应是(S1,S2,S3,S4)构成的分块循环矩阵,Si(i=1, 2, 3, 4)为 9 × 9 的 矩 阵 。 由 式(7)得


经计算,得到细分矩阵S2的特征值从大到小依次为:由于细分矩阵S2对应的特征映射无法用具体代数形式表示,可通过分析其特征值及对应于第二、第三特征值的特征映射构成的特征环(见图9)的性质,判断其单射性和正则性。

图9 新的Midedge格式正则区域的特征环Fig.9 Characteristic rings of Midedge subdivision in regular regions
特征映射指将原来的参数化网格映射到[v2v3]所构成的新网格上,即将如图8所示的细分矩阵S2的初始网格映射到如图9所示的[v2v3]所构成的新网格(将[v2v3]看作二维点所构成的列向量)上。另外,从图9所示的细分矩阵S2的特征环中可以看出,该特征映射将一个具有25个面片的网格映射为一个具有25个网格的面片,在基本的二元二阶B样条基下(即bk(u v j)取相应的B样条基函数),特征环的边一定是原来图像中的边,说明该特征映射是单射的。至于特征映射的正则性,其实就是相应的雅可比行列式不为零。在同样的基下,由图8和图9相似即可得到。所以,细分矩阵S2满足前述2个条件,本文所提出的细分格式的极限曲面是正则的(C1连续)。
4 边界规则和特殊点规则
4.1 边界规则
对于非封闭的初始网格,如对图10中的边P22P32插入新的点,则本文所设计的细分模板便不再适用。为此,引入虚拟点P21,P31,P41,

使模板能够适用。此即为用于本文提出的细分格式的边界规则。
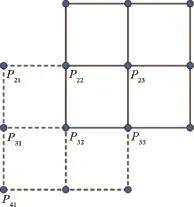
图10 边界处理Fig.10 Boundary treatment
4.2 特殊点规则
4.2.1 特殊点掩模
对于图11所示的初始网格特殊点(即点的价不再是标准的4),细分时所对应的掩模也要有相应的变化。
此时,图中Pk+1,Pk+2的掩模保持不变,对P1~Pk的掩模做特殊处理,P的生成规则为

4.2.2 特殊点处细分的连续性
本节,以k=3,5时的特殊点为例,验证新的Midedge格式在特殊点时的连续性。
此时对应于价为3的特殊点,本文提出的细分格式所对应的模板如图12所示。相应的2步细分
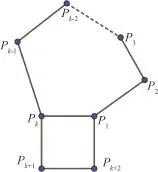
图11 k价特殊点模板Fig.11 Extraordinary point stencil of the valence k
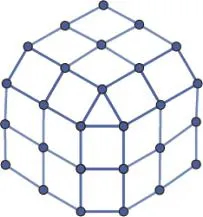
图12 特殊点价为3时的细分模板Fig.12 Extraordinary point stencil of the valence 3

图13 矩阵的特征环Fig.13 Characteristic rings of matrix
同理可得,k为5时所对应的细分模板,细分矩阵对应的特征环如图14所示。相应地,2步细分矩阵为(S51,S52,S53,S54,S55),所对应的分块循环矩阵为,其中S5i(i=1,2,… ,5)为 9 × 9 的 矩阵。可以求出矩阵的特征值为,且各个特征值都不为0,细分矩阵对应于第2、第3特征值的特征映射构成的特征环如图15所示,至此,验证了价为3,5的特殊点处此细分格式所生成的极限曲面也是正则的(C1的)。可采用同样的方式验证其他价的特殊点,在此不再赘述。

图14 特殊点价为5时的细分模板Fig.14 Extraordinary point stencil of the valence 5

图15 矩阵的特征环Fig.15 Characteristic rings of matrix
5 数值实验
图16和图17分别为对不含特殊点的初始控制网格使用新的Midedge格式和原始的Midedge格式细分4次后的图像,图18为初始网格为正方体的网格图像细分7次后的图像。图19为与之对应的使用原Midedge格式的效果图。图21为7个正方体构成的多面体细分前后的图像对比。图22为与之对应的使用原Midedge格式的效果图。

图16 正则网格上新的Midedge细分Fig.16 New Midedge subdivison on regular mesh

图17 正则网格上的Midedge细分Fig.17 Midedge subdivison on regular mesh

图18 正方体网格经7次新Midedge细分后的图像Fig.18 A cube mesh after new Midedge subdivision for 7 times
从图21和22可以看出,本文的细分格式具有良好的收敛性和连续性。由于所提出的细分格式是一种逼近型格式,舍弃了初始网格控制点,使细分前后网格曲面大小不同。通过对比还发现,虽然新格式在大小保留上不及原始Midedge格式好,但是在特殊点处理上,新格式更为平滑,详见图20(为图18、图19特殊点处的截图)。

图19 正方体网格经7次Midedge细分后的图像Fig.19 A cube mesh after Midedge subdivision for 7 times
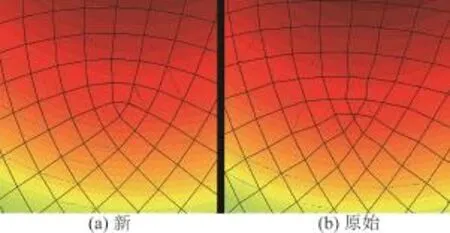
图20 新与原始Midedge细分局部图Fig.20 Parts of images with new and origin Midedge subdivisions

图21 新Midedge细分后的图像Fig.21 Mesh with new Midedge subdivision
6 结 论
给出了一种通过扩充已有细分模板得到新的细分模板的思路,并对REIFU的Midedge细分格式进行了模板扩充,使用曲线的三点二重逼近格式,确定新模板的掩模。得到的新的Midege型逼近型曲面细分格式,具有良好的连续性,且证明了该细分格式至少是C1连续的。

图22 Midedge细分后的图像Fig.22 Mesh after Midedge subdivision
