李军成，刘成志，易叶青

（1.湖南人文科技学院数学与金融学院，湖南娄底417000；2.湖南人文科技学院信息学院，湖南娄底417000）

在计算机辅助设计及其相关研究领域中，插值曲线的构造一直都是重要的研究课题。作为一种分段插值样条，三次Cardinal样条［1］是构造插值曲线的一种重要方法。三次Cardinal样条不仅满足C1连续，而且无须求解方程系统即可直接插值于给定的数据点。另外，当数据点保持不变时，三次Cardinal样条的插值效果还可通过自带的张力参数进行调控。这些优点使得三次Cardinal样条被广泛应用于多工程领域［2-3］。 虽然，三角Cardinal样条［4-5］、双曲 Cardinal样条［6］以及C2连续的 Cardinal样条［7］在某些方面较传统三次Cardinal样条更优，但它们的方程结构更为复杂，因此不可否认，传统三次Cardinal样条仍具有较高的应用价值。

注意到，张力参数对三次Cardinal样条的形状有明显的影响，为了使三次Cardinal样条能插值于给定的首、末数据点，往往需要在数据点的两端添加2个边界条件，故边界条件对首、末两段样条曲线的形状也有较大影响。因此，在利用三次Cardinal样条构造插值曲线时，可通过修改张力参数和边界条件来实现对插值效果的调控，这显然为插值曲线的构造提供了便利。当然，也可以在某种准则下确定张力参数和边界条件的最佳取值，使得构造的三次Cardinal样条满足某种特定的要求。为使三次Cardinal样条曲线尽可能光顺，文献［8］提出了一种利用曲率变化极小来确定张力参数和边界条件最佳取值的方法。但文献［8］仅简单给出了确定张力参数和边界条件最佳取值的方法，对其具体过程以及相应的三次Cardinal样条函数并未展开详细讨论。为此，本文进一步讨论如何通过优化张力参数与边界条件以使得构造的平面三次Cardinal样条曲线及其函数形式尽可能光顺的方法。通过对平面三次Cardinal样条曲线及其函数形式的近似曲率变化进行极小化，易获得张力参数与边界条件的唯一解，从而使构造的三次Cardinal样条曲线及其函数形式尽可能光顺，且具有更好的插值效果。

1 问题的提出

给定平面上n(n≥3)个数据点pi(i=0,1,…,n)，三次 Cardinal参数样条曲线［1］可表示为

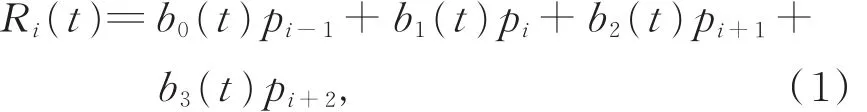
式 中 ，i=1,2,…,n-2，0≤t≤ 1，bj(t)(j=0,1,2,3)为

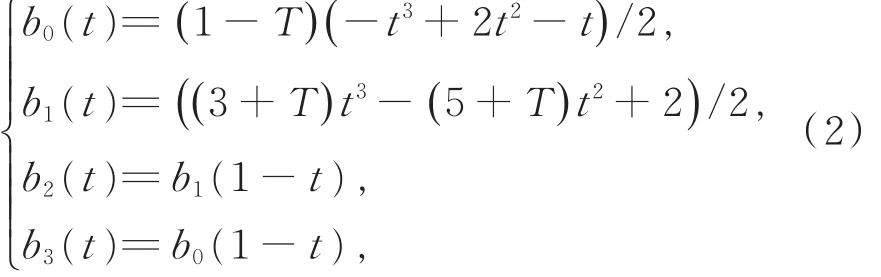
其中，实数T称为张力参数。

特别地，当三次Cardinal样条用于插值用途时，张力参数的最佳值取为T=0［9］，此时对应的三次Cardinal样条又称为三次Catmull-Rom样条［10］。三次Catmull-Rom样条在许多工程领域已得到了较广泛的应用［11-12］。

由式（1）与式（2）不难发现，当T=1时，式（1）为

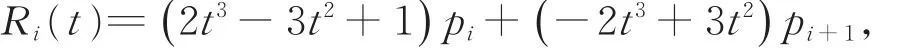
此时三次Cardinal参数样条曲线将退化为一条直线段。因此，下面仅考虑T≠1的情形。

式（1）与式（2）经计算可得，

式（3）表明，每段三次Cardinal参数样条曲线插值于第2与第3个数据点，意味着整条样条曲线插值于除首、末数据点以外的其他数据点。由式（4）可得，表明三次Cardinal参数样条曲线满足C1连续。另外，由式（4）不难发现，当所有数据点保持不变时，三次Cardinal参数样条曲线的形状将由张力参数T决定。例如，给定数据点pi(i=0,1,…,5)的坐标(xi,yi)为

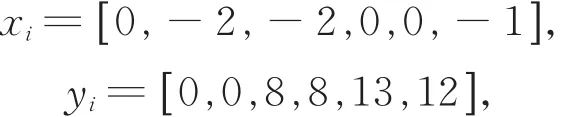
张力参数T取不同值时的三次Cardinal参数样条曲线如图1所示。

另一方面，在许多实际问题中往往要求三次Cardinal参数样条曲线也能插值于首、末数据点，此时，须在数据点pi(i=1,2,…,n)的两端补充2个边界条件：p-1与pn+1，常用的边界条件取为p-1=p0，pn+1=pn。而事实上，当张力参数T固定，2个边界条件取不同点时，首、末两段三次Cardinal参数样条曲线的形状也将不同。例如，对于图1中给定的数据点，取张力参数T=0，2个边界条件取不同点时的三次Cardinal参数样条曲线如图2所示，图中虚线对应的边界条件为p-1=p0，p6=p5；实线对应的边界条件为p-1=p2，p6=p3。

综上，当数据点给定时，三次Cardinal参数样条曲线的形状由张力参数T以及2个边界条件p-1与pn+1决定。理论上，可根据不同的需求将张力参数和边界条件取为任意值。当然，也可对张力参数与边界条件进行优化，得到满足特定要求的三次Cardinal参数样条曲线。

2 张力参数与边界条件的优化

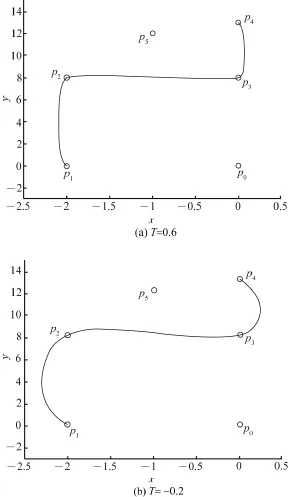
图1 张力参数取不同值时的三次Cardinal参数样条曲线Fig.1 Parametric cubic Cardinal spline curve with different tensor parameters

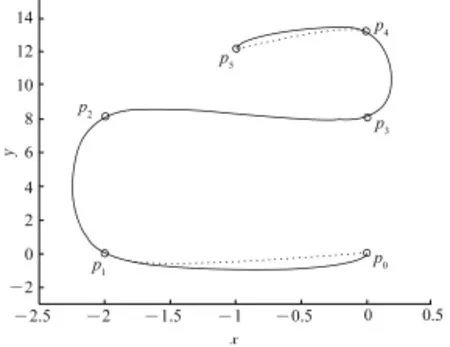
图2 边界条件取不同点时的三次Cardinal参数样条曲线Fig.2 Parametric cubic Cardinal spline curve with different boundary condition

光顺性是曲线的重要几何特征之一。在CAD及其相关研究领域，构造光顺的曲线是一项重要的研究课题［13-14］。虽然曲线的光顺性无法定量描述，但人们通常通过极小化曲线的能量函数来实现平面光顺曲线的构造［15］。应变能量和曲率变化能量成为研究人员描述平面曲线光顺性的2种常见方法［16-19］。本文利用曲率变化能极小来优化平面三次Cardinal参数样条的张力参数和边界条件，使得构造的样条曲线尽可能光顺。

平面参数曲线r(t)的曲率变化能定义为［20］

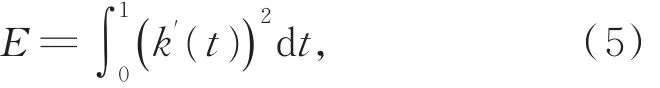
式中，

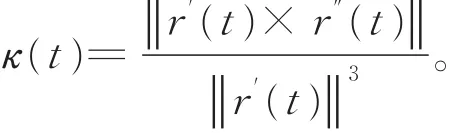
由于式（5）高度非线性，往往需要利用近似形式将其线性化。假设曲线r(t)被弧长近似参数化，则其曲率变化能可近似表示为［21］

为讨论方便，令T=1-2α，则式（2）可改写为

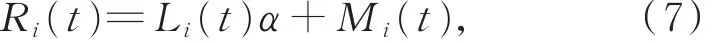
式中，

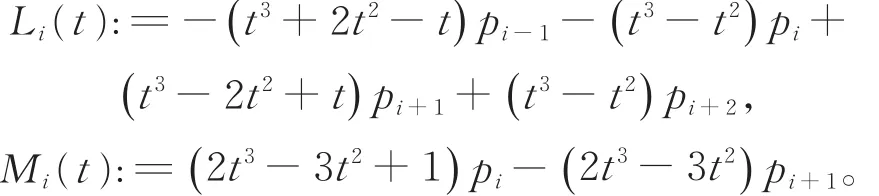
于是，据式（6）与（7），补充边界条件p-1与pn+1后的三次Cardinal参数样条曲线的应变能可近似表示为

式中，

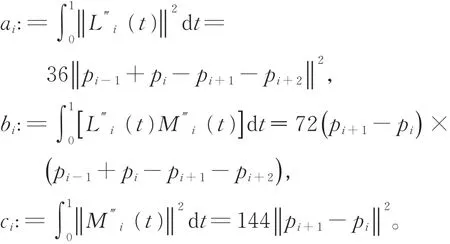
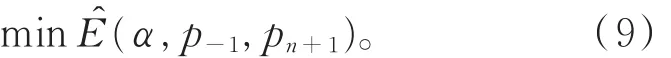
为了求解问题（9），首先给出以下引理。

引理1 给定平面上的向量a=(ax,ay)，b=

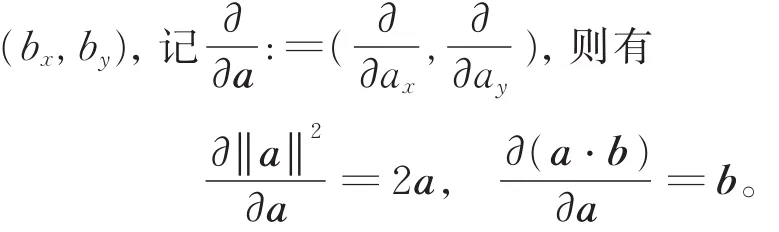
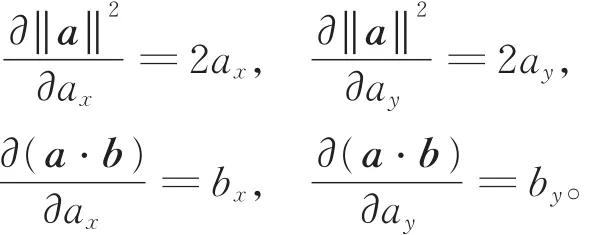
于是，

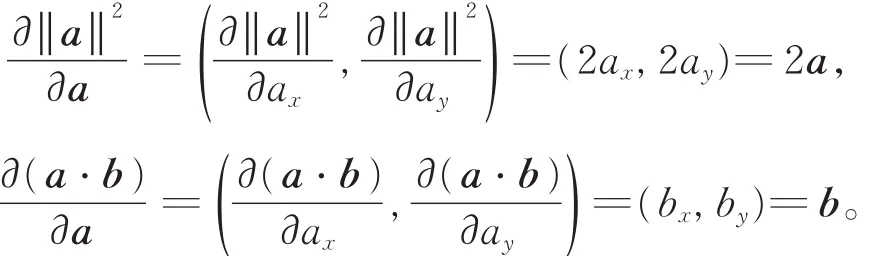
证毕。

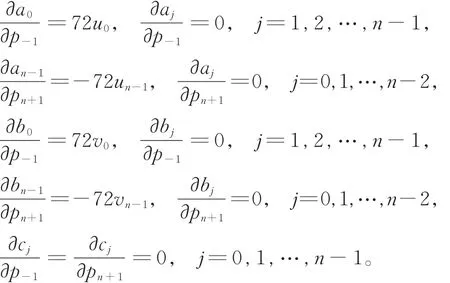
于是，

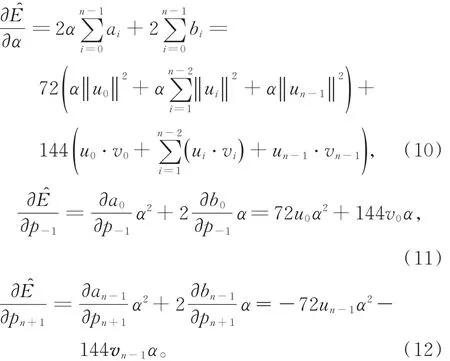
于是有

定理1 给定平面上一列数据点pi(i=0,1,…,n)，要使所构造的三次Cardinal参数样条曲线具有极小近似的曲率变化能，则张力参数T(T≠ 1)与2个边界条件p-1与pn+1应分别取为

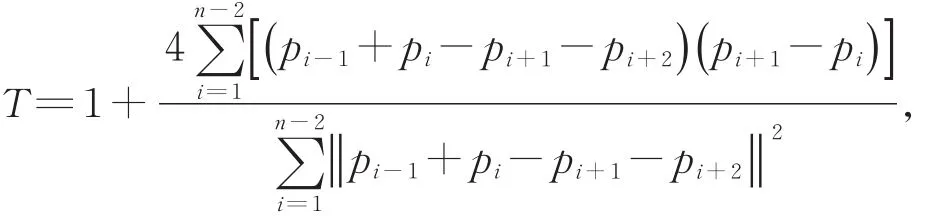
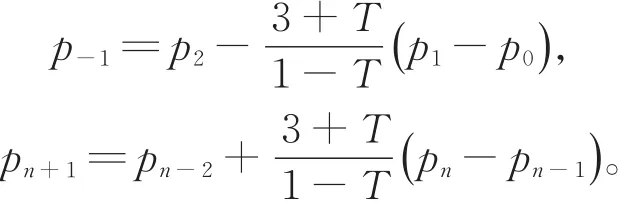
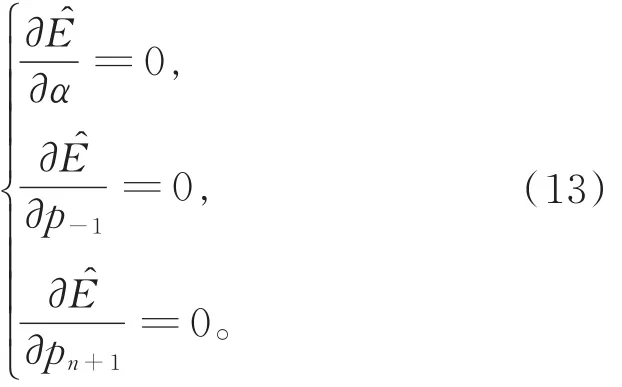
由式（11）与式（12），当α≠ 0时，令与，可得

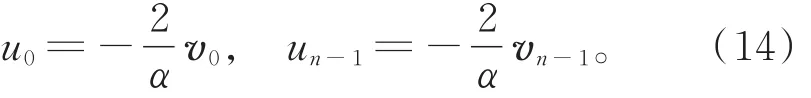
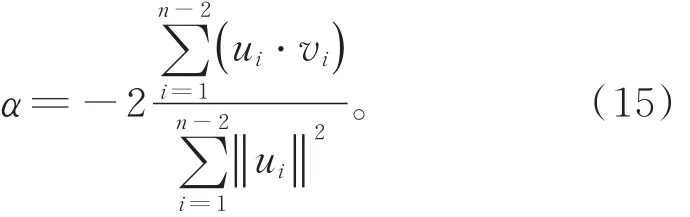
将ui=pi-1+pi-pi+1-pi+2，vi=pi+1-pi，α=分别代入式（14）与式（15），并经简单推导即得定理成立。证毕。

下面通过数值实例来说明本文方法的有效性。由于三次Catmull-Rom样条被视为三次Cardinal样条中插值效果最好的［9］，因此，本文将与三次Catmull-Rom参数样条曲线进行比较，且三次Catmull-Rom参数样条曲线的边界条件取常用情形，即p-1=p0，pn+1=pn。

例1 对于图1中给定的数据点，要使所构造的三次Cardinal参数样条曲线具有极小的近似曲率变化能，经计算所得张力参数、2个边界条件及近似曲率变化能与三次Catmull-Rom参数样条曲线的对比如表1所示。

构造的具有极小近似曲率变化能的三次Cardinal参数样条曲线（实线）与三次Catmull-Rom参数样条曲线（点虚线）如图3所示。

例2 从单位半圆上取定数据点pi(i=0,1,…,5)的坐标(xi,yi)为

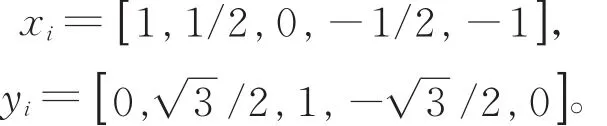
表1 本文方法与Catmull-Rom的对比（例1）Table 1 The comparison between the proposed method and Catmull-Rom（example 1）

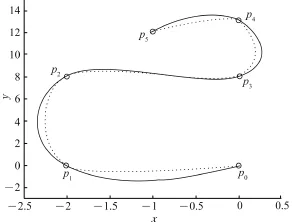
图3 具有极小近似曲率变化能的三次Cardinal参数样条曲线（例1）Fig.3 Parametric cubic Cardinal spline curve with minimum approximate curvature variation energy（example 1）

要使所构造的三次Cardinal参数样条曲线具有极小的近似曲率变化能，经计算可得张力参数、2个边界条件及近似曲率变化能与三次Catmull-Rom参数样条曲线的对比如表2所示。

构造的具有极小近似曲率变化能的三次Cardinal参数样条曲线（实线）与三次Catmull-Rom参数样条曲线（长虚线）如图4所示。

由例1与例2可知，张力参数与边界条件优化后的三次Cardinal参数样条曲线较三次Catmull-Rom参数样条曲线更为光顺，插值效果更好。

表2 本文方法与Catmull-Rom的对比（例2）Table 2 The comparison between the proposed method and Catmull-Rom（example 2）

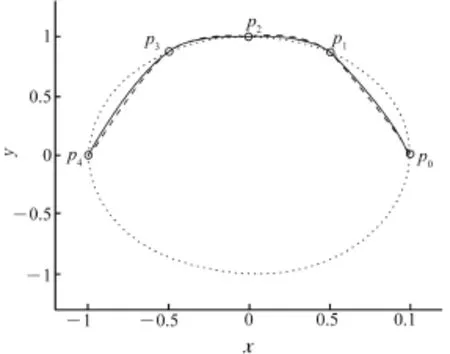
图4 具有极小近似曲率变化能的三次Cardinal参数样条曲线（例2）Fig.4 Parametric cubic Cardinal spline curve with minimum approximate curvature variation energy（example 2）

3 三次Cardinal样条函数

与三次Cardinal参数样条曲线对应，本节讨论三次Cardinal样条函数。

给定平面上n(n≥3)个数据点(xi,yi)(i=0,1,…,n)，设xi为等距，即xi+1-xi=h（h为常数），三次Cardinal样条函数可表示为

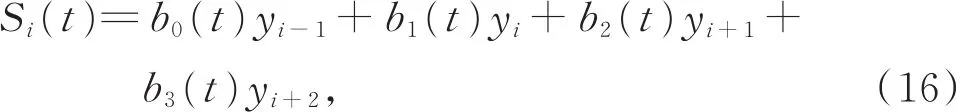
式 中 ，i=1,2,…,n-2，xi≤x≤xi+1，t=(xxi)/h，bj(t)(j=0,1,2,3)为式（2）表示的函数。

由式（2）不难验证，

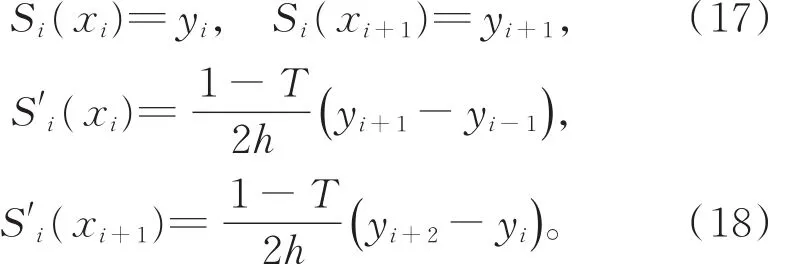
由式（17）与式（18）可知，三次Cardinal样条函数插值于除首、末数据点外的其他数据点，且函数满足C1连续。同样，可以补充2个边界条件(x-1,y-1)与(xn+1,yn+1)，使得三次Cardinal样条函数插值于包括首、末数据点在内的所有数据点。由于要求xi为等距，故有x-1=2x0-x1，xn+1=2xn-xn-1。显然，当所有数据点保持不变时，三次Cardinal样条函数的形状由张力参数T以及2个边界条件y-1与yn+1决定。

与三次Cardinal参数样条曲线的情形类似，三次Cardinal样条函数满足

定理2 给定平面上一列数据点(xi,yi)(i=0,1,…,n)，要使所构造的三次Cardinal样条函数具有极小的曲率变化能，则张力参数T(T≠1)与2个边界条件y-1与yn+1应分别取

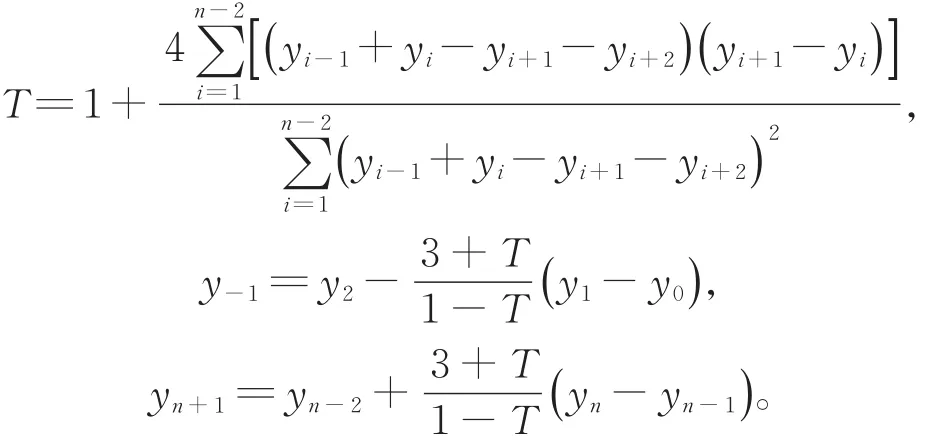
下面通过数值实例来说明本文方法的有效性，同上节，将本文方法与三次Catmull-Rom样条函数进行比较，且三次Catmull-Rom样条函数的边界条件为常用情形，即y-1=y0，yn+1=yn。

例 3 设y=sinx(0≤x≤ 2π)，取yi=sinxi(i=0,1,…,8)。 要 使 所 构 造 的 三 次Cardinal参数样条曲线具有极小的近似曲率变化能，经计算得张力参数与2个边界条件分别为T=-0.171 6，y-1=-0.707 1，y9=0.707 1。 构 造 的具有极小近似曲率变化能的三次Cardinal样条插值函数（实线）与三次Catmull-Rom样条插值函数（点虚线）及对应的绝对误差曲线如图5所示。

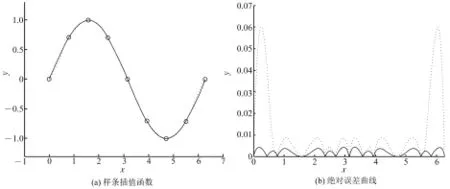
图5 样条插值函数及其绝对误差曲线（例3）Fig.5 Spline interpolation functions and the absolute error curves（example 3）

图6 样条插值函数及其绝对误差曲线（例4）Fig.6 Spline interpolation functions and the absolute error curves（example 4）

由例3与例4可知，优化张力参数与边界条件后的三次Cardinal样条函数较三次Catmull-Rom样条函数的插值效果更好。

4 结 语

当数据点给定时，三次Cardinal样条的形状完全由张力参数和边界条件决定。虽然通过修改张力参数与边界条件可实现对三次Cardinal样条形状的调控，但有时只要求得张力参数和边界条件的最佳值，就能使构造的三次Cardinal样条满足某种特定的要求。为此，本文给出了一种利用曲率变化能极小来优化三次Cardinal样条的张力参数与边界条件的方法，该方法容易获得张力参数与边界条件的唯一解。相对于三次Catmull-Rom样条，优化张力参数与边界条件后的三次Cardinal样条不仅更为光顺，而且插值效果更好。