何 军, 刘衍民

(遵义师范学院 数学学院， 贵州 遵义 563006)

1 预备知识

张量特征值问题在优化、图像处理和高阶马尔科夫链等许多科学领域中都具有重要应用[1-12].张量广义特征值[13]是矩阵广义特征值的推广.

令A=(ai1i2im)，ai1i2im∈C(复数集).下面给出与本文相关的几个定义.

定义1[1]设A∈C[m,n](m阶n维)，若存在非零向量x∈Cn和数λ∈C使得

Axm-1=λx[m-1]，

其中，n维向量Axm-1和x[m-1]定义如下：

则称λ为张量A的一个特征值，x为张量A的属于λ的特征向量.如果向量x是实向量，则称特征值λ为张量A的H-特征值，x为属于λ的H-特征向量.

一个m阶n维张量A的行列式det(A)可以看成齐次非线性方程组Axm-1=0的解[1].设A∈C[m,n]，B∈C[m,n]，α∈C，β∈C，如果

det(αA-βB)≠0，

则称{A,B}为一个正则张量对；如果

det(αA-βB)=0，

则称{A,B}为奇异的张量对.

定义2[13]设A∈C[m,n]，B∈C[m,n]，若存在非零向量x∈Cn和数α∈C，β∈C使得

βAxm-1=αBx[m-1]，

则称(α,β)为正则张量对{A,B}的一个特征值，x为其对应的特征向量.

利用张量的无穷大范数，Ding等[13]给出了张量广义特征值的盖尔圆盘定理.

引理1[13]设{A,B}是一个正则张量对，(aii,bii)≠(0,0)，i=1,2,,n，则

(1)

其中，λ(A,B)表示正则张量对{A,B}的谱，

Di(A,B):={(α,β):|βaii-αbii|≤

本文利用张量广义特征值的性质，给出了张量广义特征值的新包含域.同时把本文得到的新包含域通过理论推导以及数值例子与文献[13]中的结果(1)作比较，说明本文结果优于文献[13]中的结果(1).

2 主要结果

令

|βaijj-αbijj|，

可得张量广义特征值的新包含域(定理1).

定理1设{A,B}是一个正则张量对，(aii,bii)≠(0,0)，i=1,2,,n,则

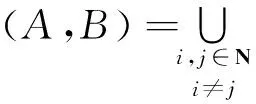
(2)

其中

Δi,j(A,B):={(α,β):(|βaii-αbii|-

|βaijj-αbijj|Rj(A,B)}.

证明设非零向量x∈Cn是正则张量对{A,B}的特征值(α,β)对应的特征向量，即

βAxm-1=αBx[m-1].

(3)

令|xp|≥|xq|≥max{|xi|:i∈N,i≠p,q}，N={1,2,,n}，由(3)式可得

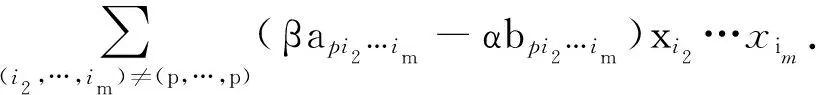
在(4)式两边同时取绝对值有

|βapp-αbpp||xp|m-1≤

|xi2||xim|，

即

|βapp-αbpp||xp|m-1≤

|βapqq-αbpqq||xq|m-1.

(5)

情形1当xq=0时，由(5)式可得

此时显然有

(α,β)∈Δ(A,B).

情形2当xq≠0时，有

|βaqq-αbqq||xq|m-1≤

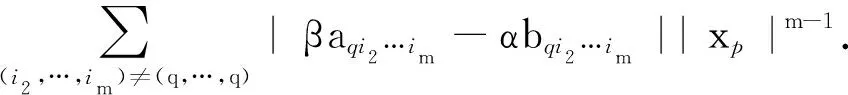
由(5)和(6)式可得

|βapqq-αbpqq|Rq(A,B).

证毕.

令N={1,2,,n}，S是N的一个非空真子集，则可得张量广义特征值的另外一个新包含域.

定理2设{A,B}是一个正则张量对，(aii,bii)≠(0,0)，i=1,2,,n,则

λ(A,B)∈ΔS(A,B)=

证明设非零向量x∈Cn是正则张量对{A,B}的特征值(α,β)对应的特征向量，即

βAxm-1=αBx[m-1]，

(7)

令

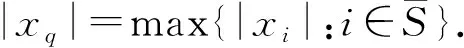
下面分3种情形进行讨论.

情形1如果xpxq≠0，不失一般性，设

|xp|≥|xq|，

则有

|βapp-αbpp||xp|m-1≤

|βapqq-αbpqq||xq|m-1，

(8)

且有

|βaqq-αbqq||xq|m-1≤

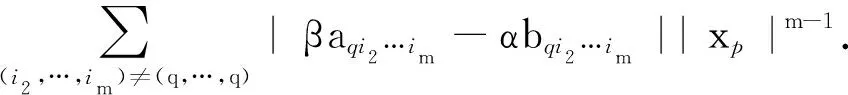
由(8)和(9)式可得

|βapqq-αbpqq|Rq(A,B),

即有

(α,β)∈ΔS(A,B).

情形2如果xpxq=0，不失一般性，设

|xp|≥|xq|=0,

由(8)式可得

即有

(α,β)∈ΔS(A,B).

证毕.

定理3设{A,B}是一个正则张量对，(aii,bii)≠(0,0)，i=1,2,,n，n≥2,则

ΔS(A,B)⊆Δ(A,B)⊆D(A,B).

证明显然可得

ΔS(A,B)⊆Δ(A,B).

下面证明

Δ(A,B)⊆D(A,B).

由定理1有，存在i≠j，使得

(α,β)∈Δi,j(A,B),

即

|βaijj-αbijj|Rj(A,B).

情形1若

|βaijj-αbijj|Rj(A,B)=0，

则有

βajj-αbjj=0，

或者

即有

(α,β)∈D(A,B).

情形2若

|βaijj-αbijj|Rj(A,B)≠0，

则有

即

或者

也即

(α,β)∈Di(A,B),

或者

(α,β)∈Dj(A,B),

即有

(α,β)∈D(A,B).

证毕.

3 数值例子

下面用数值例子来说明结果的有效性.

设A∈R[3,2]，B∈R[3,2]且

a111=1,a121=2,a211=3,

a221=4,a112=5,a122=6,

a212=7,a222=0,

b111=1,b222=2,

那么张量B是非奇异的，即正则张量对{A,B}的特征值(α,β)中的β≠0，令λ=α/β，由Matlab的工具箱TenEig[14]可得正则张量对{A,B}的谱

λ(A,B)={-3.660 6+2.032 9i,

-0.488 4+0.000 0i,9.809 6+0.000 0i,

9.809 6-0.000 0i}.

由图1可以看出，定理1的结果比引理1[13]的结果好.

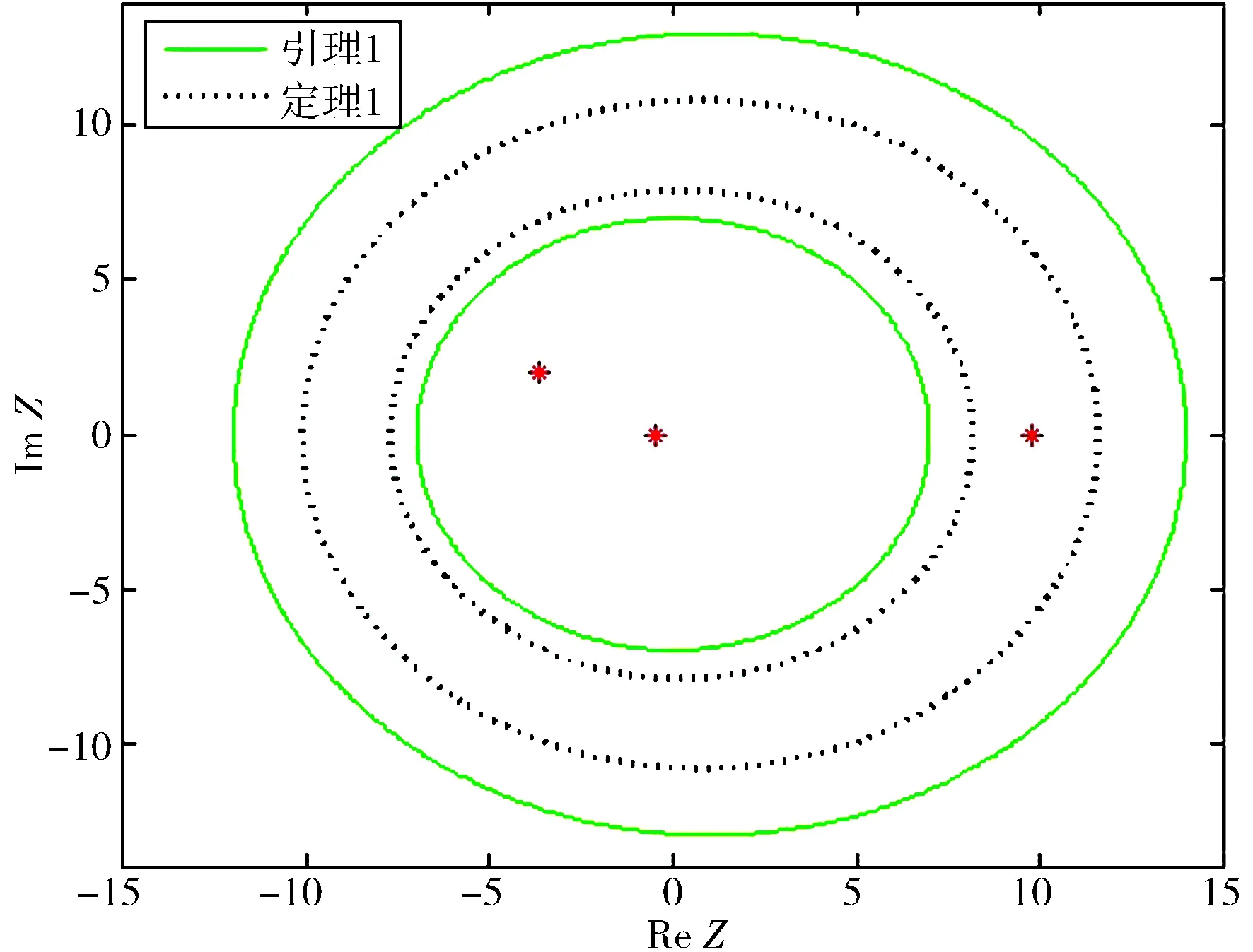
图 1 D(A,B)(实线)对比Δ(A,B)(虚线)(λ=α/β)