ZHANG Jian,ZHANG Yue-wen,WANG Fang,ZHAO Xi-lu,CUI Wei-cheng,ZHU Yong-mei

(1.School of Mechanical Engineering,Jiangsu University of Science and Technology,Zhenjiang 212003,China;2.Shanghai Engineering Research Center of Hadal Science and Technology,Shanghai Ocean University,Shanghai 201306,China;3.College of Mechanical Engineering,Saitama Institute of Technology,Saitama 369-0293,Japan)

Abstract:This paper investigated the strength characteristics of maraging steel spherical pressure hulls for deep manned submersibles.A set of analytical formulae are derived to calculate the linear elastic strength,stability,and stiffness of hulls using thick-walled shell theory,which are also compared with thin-walled shell theory and relevant empirical equations used in current classification society rules.The nonlinear buckling of hulls are numerically studied under various wall thicknesses,imperfection sizes,yield strengths,and Young’s modulus.Based on the numerical results and shell theory,a semi-analytical formula is deduced to predict the nonlinear buckling loads of spherical hulls.The strength characteristics of a maraging steel spherical pressure hull used in a full ocean depth manned submersible are numerically and analytically studied as an example,which agrees well with each other.The results show that the proposed formulae can quite accurately predict the strength of maraging steel spherical pressure hulls.This work can provide a foundation to develop the next generation design rules of deep manned pressure hulls.

Key words:spherical shell;pressure hull;maraging steel;buckling;numerical method

0 Introduction

Deep manned submersibles have long received much attention,via which human beings can dive thousands of meters into deep sea to carry out various activities(Cui,2013)[1].The pressure hull is one of the most important components and buoyancy units of deep manned submersibles,providing an atmospheric space for the carried crew and non-pressure resistant equipment.Spherical shell is the most optimal shape of deep pressure hulls due to the uniform stress and strain distributions in the material(Pan and Cui,2010[2];Pan and Cui,2011[3]).Typical deep manned submersibles employing the spherical pressure hull are Jiaolong,Alvin,New Alvin,MIR I and II,Consul,RUS,Nautile,Shinhai 6500,and Deepsea challenger.Under the development of full ocean depth manned submersible ‘RainbowFish’,our team also se-lects the spherical shape as its manned cabin(Cui et al,2015)[4]and intends to use extremely high strength maraging steel.However,the strength characteristics of maraging steel spherical pressure hulls like nonlinear buckling have not been well studied(Blachut,2013[5];Ifayefunmi,2016[6];Blachut and Magnucki,2008[7]).

Titanium alloy is the most popular material used to fabricate deep spherical pressure hulls due to its low mass density and high yield strength(Ross,2006)[8].Maraging steel is another attracting material particularly in the case for full ocean depth due to its extremely high strength,high ductility,and ease of manufacturing(Wang et al,2016)[9].Numerous studies concerning the strength characteristics of titanium spherical pressure hulls have been performed in recent years.Pan et al conducted an overview of buckling and ultimate strength of deep spherical pressure hulls and a comparison of different rules for the hulls.They found that current rules cannot be used to design the deep spherical pressure hulls(Pan and Cui,2011)[3].Using numerical and experimental results of titanium alloy spherical pressure hulls,they developed a phenomenological model to predict the ultimate strength of deep spherical pressure hulls,which has been adopted in the Chinese Classification Society rules(CCS2013)(Pan et al,2010[10];Pan and Cui,2012[11];CCS,2013[12]).As deep spherical pressure hulls belong to medium-thick shells of revolution,elastic-plastic buckling is their main failure mode when subjected to uniform external pressure,which is greatly affected by the yield strength and imperfection size(Lu et al,2004[13];Zhang et al,2017[14];Lee et al,2016[15]).Based on this mechanism,a semi-analytical formula was developed for titanium alloy spherical pressure hulls.The semi-analytical formula is the product of plasticity reduction factor,imperfection reduction factor,and analytical elastic buckling load.This factor-separation concept is in line with ECSC(Schmidt and Swadlo,1998)[16].Material plays a vital role in the strength characteristics of deep spherical pressure hulls.However,little attention has been paid to the maraging steel spherical pressure hulls,which is being applied to develop full ocean depth manned submersible‘RainbowFish’.

To provide theoretical support for the development of full ocean depth pressure hulls,this work focuses on the strength characteristics of deep maraging steel spherical pressure hulls.The rest of this paper is organized as follows.Chap.1 briefly introduces the current research results regarding deep spherical pressure hulls.In Chap.2,the strength,stability,and stiffness of deep spherical pressure hulls are proposed in linear range based on the analytical method.The numerical nonlinear buckling analysis of deep maraging steel spherical pressure hulls are carried out in Chap.3.As a result,a modified semi-analytical formula is developed to predict the nonlinear buckling load of maraging steel hulls,which is benchmarked against the numerical results.Chap.4 provides an analytical and numerical study into the strength characteristics of a full ocean depth pressure hull.Finally,in Chap.5,an experimental study of hemi-spherical shell is conducted to verify the formulae.The proposed formulae to evaluate the strength of deep maraging steel spherical pressure hulls can provide a foundation for the construction of the new design rules of deep manned submersibles.

1 Background

Consider a spherical pressure hull with geometry given by the ratio,η=t/r,of uniform wall thickness,t,to the median radius,r,and subjected to uniform external pressure,p0,as can be seen in Fig.1.Assume the material with Young’s modulus,E,Poisson’s ratio, μ,the yield strength, σy,and ultimate strength,σt.Strength and stability have long been considered as two most important design constraints to ensure the safety of pressure hulls.Most classification society rules for the calculation of spherical pressure hulls employ the same assumption of thin-walled shell theory(Pan and Cui,2011)[3].For example,the strength is examined based on the stress,σm,of the median surface of the hull(Eq.(1)),whilst the stability is examined based on the critical elastic buckling load,pthin,obtained from Zoelly formula(Zoelly,1915)[17](Eq.(2))along with additional reduction factors.

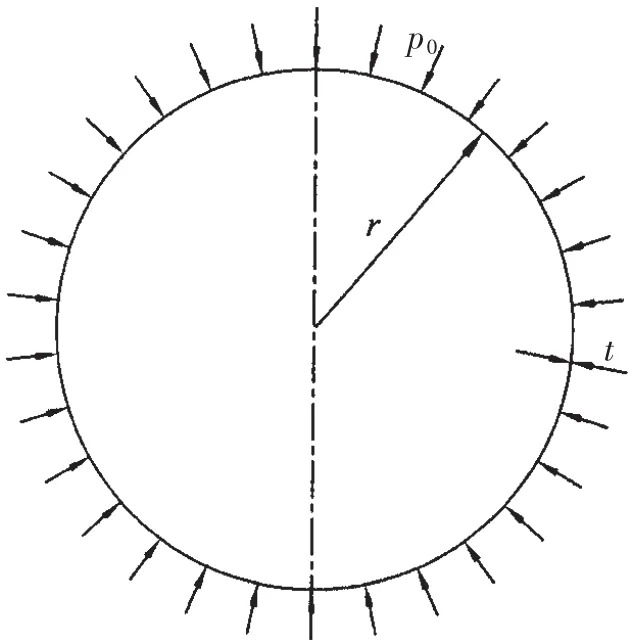
Fig.1 Schematic of a spherical pressure hull subjected to uniform external pressure,p0

However,deep spherical pressure hulls are medium-thick shells,which tend to collapse in an elastic-plastic range.Besides,the stress changes greatly in the thickness direction,in which case the stress on the inner surface is even higher than the median surface under external pressure.Pan and Cui found a contradiction between wall thickness obtained from current rules and that observed from current in-service deep pressure hulls(Pan and Cui,2011)[3].They advocated the use of average membrane stress,σccs2013,to examine the strength of deep pressure hulls,referring to Eq.(3).Also,they put forward an empirical formula(Eq.(4))to examine the stability of deep pressure hulls.Details of both formulae can be found in CCS2013(CCS,2013)[12].

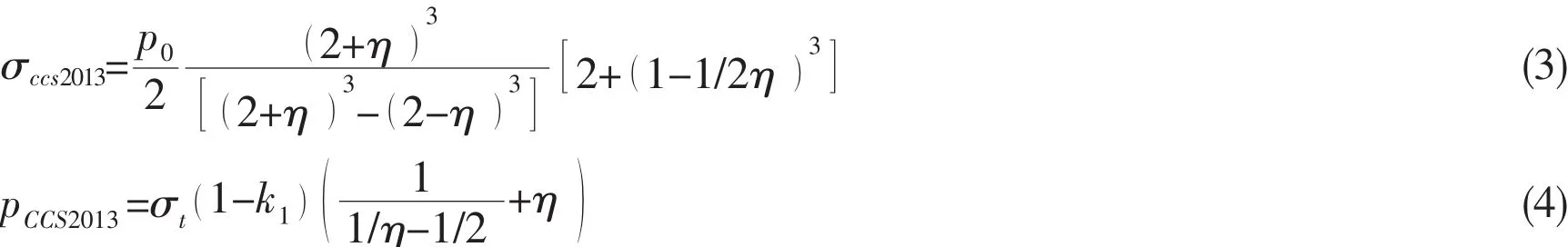
where,the fabricating deviation modified factor

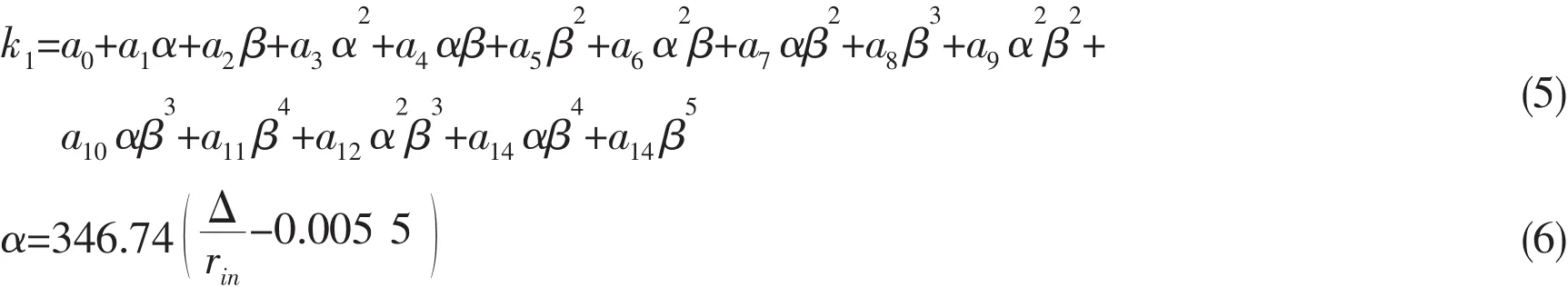
where,rin=internal radius;Δ=imperfection size;a0=0.013 59;a1=0.045 25;a2=-0.049 42;a3=0.001 285;a4=-0.023 27;a5=0.022 78;a6=-0.000 233 7;a7=0.011 38;a8=-0.010 32;a9=-0.003 564;a10=-0.001 883;a11=0.003 514;a12=0.002 121;a13=-0.000 643;a14=-0.000 677 2.Similar formula(Eq.(8))to examine the stability of deep pressure hulls can be found in their published papers(Pan et al,2010[10];Pan and Cui,2012[11]),as follows:

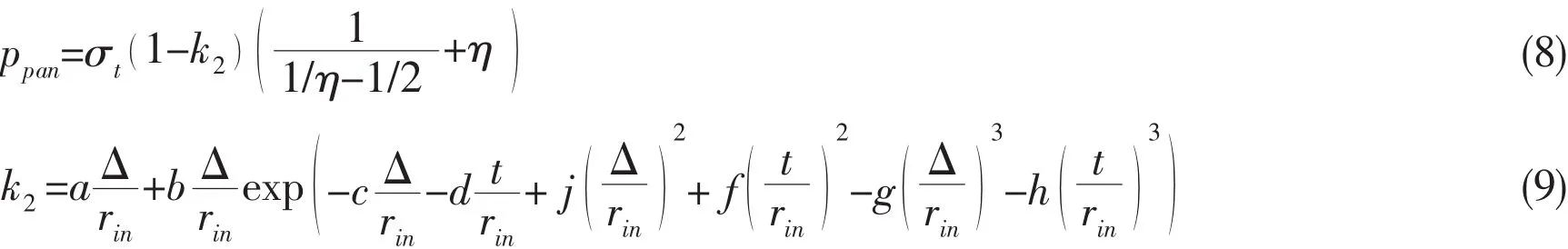
where a=15.63;b=606.6;c=264;d=72.72;j=3e4;f=882.5;g=1.2e6;h=3 969.These formulae(Eqs.(3-9))initially aimed at assessing the titanium alloy spherical pressure hulls of Chinese deep manned submersible ‘Jiaolong’.Since the stress obtained from Eq.(3)is not the analytical solutions,there may exist some errors,which should be further evaluated.Also,these empirical formulae(Eqs.(4-9))are phenomenological models defining the critical buckling load as a function of internal radius,imperfection size and material tensile strength.They exclude the most important parameters like yield strength,Young’s modulus and Poisson’s ratio.

Therefore,a semi-analytical formula(Eq.(6))to predict the nonlinear buckling load of titanium alloy spherical pressure hulls was deduced according to the numerical buckling of a family of hulls.Hulls considered had uniform thickness-to-median radius ratio,η=t/r,of 0.025-0.08,eigenmode imperfection size-to-median radius ratio, δ=Δ/r,of 0.002-0.01,and yield strength,σy,of 800-1 300 MPa.The semi-analytical formula assumes that the plasticity reduction factor is a function of the yield strength and the wall thickness-to-median radius ratio,and the imperfection reduction factor is a function of the yield strength,the wall thickness-to-median radius ratio,and the imperfection size-to-median radius ratio.

where kpis the plasticity reduction factor,kimpis the imperfection reduction factor.They can be respectively given in the following:

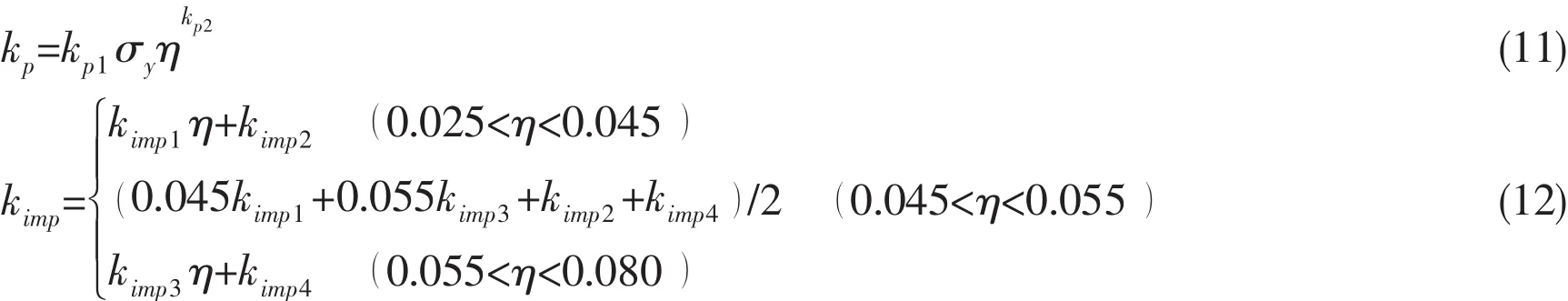
where,plastic coefficients kp1=1.62×10-5MPa-1,kp2=-0.986.Imperfection coefficients,including kimp1,kimp2,kimp3,and kimp4,depend on the imperfection size-to-radius ratio,δ,and the yield strengths,σy,which can be obtained from Fig.2.Nevertheless,whether these formulae(Eqs.(3-8))can be applied to design deep maraging steel spherical pressure hulls or not require further evaluation.

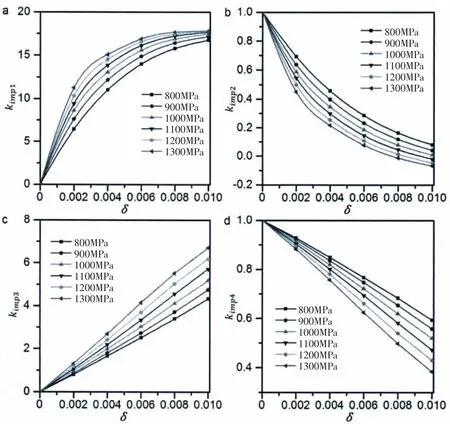
Fig.2 Imperfection coefficients,kimp1,kimp2,kimp3,and kimp4,of titanium alloy spherical pressure hulls versus the imperfection size-to-median radius ratio,δ,at yield strength,σy=800-1 300 MPa

2 Analytical analysis based on shell theory

This chapter involves evaluation of strength,stability,and stiffness of deep spherical pressure hulls.The evaluation is analytically done based on the linear elastic thick-walled shell theory,which is compared with thin-walled results as well.

2.1 Linear elastic strength

According to the thick-walled spherical shell theory(Gill,1970)[18],analytical solutions of deep spherical pressure hulls,such as the inner surface stress,σi,and the outer surface stress,σo,can be obtained as follows:

Both are functions of η=t/r under a specific uniform external pressure,p0.

Using Eq.(1),Eq.(3),Eq.(13)and Eq.(14),the stresses of spherical pressure hulls can be determined using the thin-walled shell theory,average concept,and thick-walled spherical shell theory,respectively.As can be observed in Fig.3,the maximum stress is on the inner surface,whilst the minimum stress locates on the outer surface.The stress,σm,of the median surface obtained from Eq.(1)is about the average value of inner surface stress,σi,and outer surface stress,σo.The average membrane stress,σccs2013,is 1.2%-3.8%lower than the inner surface stress,σi,although it is even higher than the stress,σm,of the median surface.These differences increase with an increase in the wall thickness-to-median radius ratio,η.These findings suggest that results obtained from current classification society rules may lead to a non-conservative evaluation of strength,the stress of deep pressure hulls should be evaluated according to Eq.(13),which can ensure the design safety from a strength point of view.In this case,the yielding load of deep pressure hulls can be determined by reordering Eq.(13):

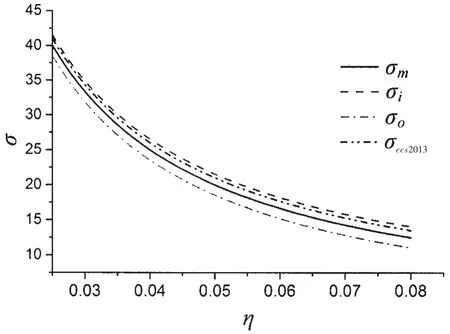
Fig.3 Linear elastic stress,σ[p0/2],versus wall thickness-to-median radius ratio,obtained from thickwalled spherical shell theory(σi, σo),thinwalled spherical shell theory(σm),and CCS2013(σccs2013).

2.2 Linear elastic stability

Similar to the linear elastic strength,the linear buckling load of deep pressure hulls is obtained in the case of thick-walled spherical shells(Wang et al,2005)[19],as follows:

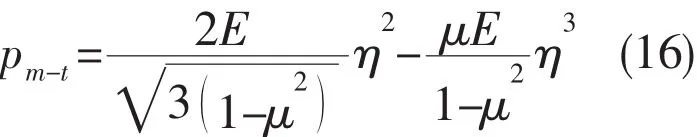
Using Eq.(2)and Eq.(16),the linear buckling loads of spherical pressure hulls can be determined with the assumptions of thin-walled and thick-walled shell theories respectively.Assume Poisson’s ratio,μ=0.3,the linear buckling load,p,versus the wall thickness-to-median radius ratio,η,can be plotted in Fig.4.As can be seen,both buckling loads are similar in the case of thin wall thickness.However,the difference between them is relatively large in the case of thick wall thickness.For example,when η=0.08,linear buckling load,pm-t,obtained from Eq.(16)is 2.2%lower than the one,pthin,which obtained from Eq.(2).Previous numerical analysis of deep spherical pressure hulls has also been confirmed that Eq.(16)can accurately assess the linear buckling of deep spherical pressure hulls(Zhang et al,2015)[20].It is indicated that stability evaluated using thin-walled shell theory may lead to a non-conservative evaluation of stability as well.The linear buckling load of deep pressure hulls should be predicted using thick-walled shell theory(Eq.(16)).

Fig.4 Linear elastic buckling load,p[E],versus wall thickness-to-median radius ratio,η obtained from medium-thick-walled theory(pm-t)and thin-walled theory(pthin)with the assumption of μ=0.3

2.3 Linear elastic stiffness

In addition,to facilitate the arrangement and design of internal and external components of deep manned submersibles connected with the deep spherical pressure hulls,it is very important to obtain the hull deformation in deep sea conditions,which indicates the stiffness of hulls.Unfortunately,all current classification society rules neglect the check of the deformation of hulls,possibly because most of them are developed focusing on shallow or medium depth submersibles.In this work,analytical study into the displacement of deep spherical pressure hulls is conducted under uniform external pressure.According to the thin-walled axisymmetric shell theory(Ventsel and Krauthammer,2001)[21],the radial displacement,um,of the meridian surface of hulls can be given by Eq.(17),whist the radial displacement,ui,of inner surface of hulls can be given by Eq.(18)using the thick-walled spherical shell theory(Gill,1970)[18],along with that,uo, of outer surface given by Eq.(19).

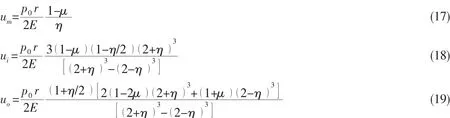
Assume Poisson’s ratio,μ=0.3,the radial displacement,u,versus the wall thicknessto-median radius ratio,η,can be plotted in Fig.5.As can be seen,all displacements decrease with an increase in η.The inner surface displacement,ui,is even higher than the outer one,uo,which is slightly higher than the one,um,obtained from the thin-walled axisymmetric shell theory.It is suggested that thin-walled assumption may lead to a nonconservative result of stiffness.The radial displacement of deep spherical pressure hulls should be predicted from Eqs.(18-19).

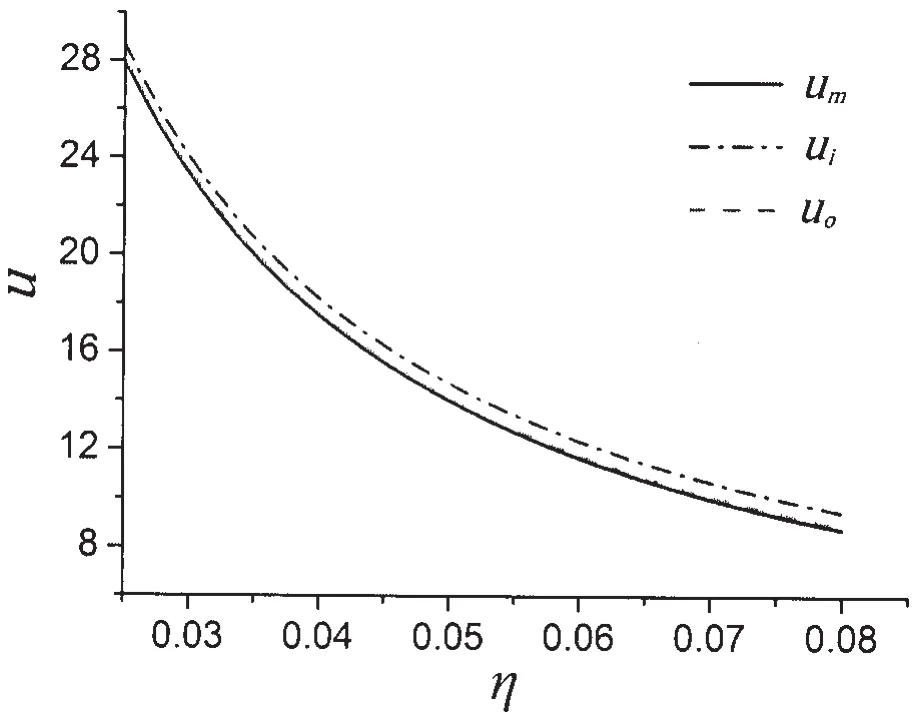
Fig.5 Radial displacement,u[p0r/(2E)],versus wall thickness-to-median radius ratio,η obtained from medium-thick-walled theory(ui,uo)and thin-walled theory(um)

3 Numerical nonlinear buckling analysis

Previous studies have showed that the linear elastic predicted buckling load of spherical shell is even higher than the experimental results,due to the existence of material nonlinearity,geometrical nonlinearity,and inevitable imperfection(Blachut,2013)[5].Using regression analysis of nonlinear numerical buckling results of perfect and imperfect hulls,this chapter derives a semi-analytical formula to examine the nonlinear buckling load of deep maraging steel spherical pressure hulls.

3.1 Numerical methodology

Spherical pressure hulls considered have a median radius of r=1 000 mm,a uniform wall thickness of t=25-80 mm with the increment of 5 mm.Referring to the pretest of maraging steel,it is assumed that the material properties are as follows:Young’s modulus E=200 GPa,Poisson’s ratio μ=0.3,yield strength σy=1 600-2 300 MPa with the increment of 100 MPa.

Series of numerical experiments are carried out according to ENV 1993-1-6(2007)(ENV,2007)[22]and CCS2013(CCS,2013)[12],which include 96 geometrically and materially nonlinear analyses(GMNA)and 480 geometrically and materially nonlinear analyses with imperfections included(GMNIA).The mesh,load,boundary condition,material modeling,imperfection definition and analysis method are nearly the same as those of previous studies regarding deep titanium alloy spherical pressure hulls.For example,the mesh implements the fully integrated four-node quadrilateral shell element S4 to prevent hourglass.The mesh density convergence study(Jasion and Magnucki,2007)[23]in the case of linear elastic bifurcation analysis leads to 6534 shell elements for each model.A unit uniform pressure,p0=1 MPa,is applied on the external surface of each hull.Three spatial nodes of each hull are constrained in line with CCS2013(CCS,2013)[12],as follows:Uy=Uz=0,Ux=Uy=0,Uy=Uz=0.The material is assumed to be perfectly elastic-plastic modeling,which has been widely used to analyze shells of revolution under external pressure and can yield nearly the same results as elastic-plastic modeling(Blachut et al,2013)[24].The first eigenmode geometric imperfection is introduced on the perfect model to study the imperfect one with the size of 2 mm,4 mm,6 mm,8 mm,and 10 mm.The modified Riks method(Silvers,2012)[25]is selected to solve the nonlinear buckling problem based on ABAQUS code.

3.2 Results and discussion

Since the buckling mechanism of deep maraging steel spherical pressure hulls as well as the effect of wall thickness and imperfection size on the buckling are identical with titanium alloy hulls,this section only focuses on the derivation of the semi-analytical formula to predict the nonlinear buckling load.From the numerical results,the plasticity reduction factor,kp=pGMNA/pm-t,can be determined in Fig.6(a),which is plotted as the ratio of the buckling load,pGMNA,obtained from GMNA to the one,pm-t,obtained from Eq.(16).Also,the imperfection reduction factor,kimp=pGMNIA/pGMNA,can be determined in Fig.7,which is plotted as the ratio of the buckling load,pGMNIA,obtained from GMNIA to the one,pGMNA,obtained from GMNA.As a result,the same formulae as Eqs.(10-12)can be derived,except that plastic coefficients are different from titanium alloy,as follows:kp1=8.92×10-6MPa-1,kp2=-0.986.Also,imperfection coefficients,kimp1,kimp2,kimp3,and kimp4can be given by Fig.8.This finding suggests that Eqs.(10-12)may be applied to deep spherical pressure hulls made of other various materials via modifying the plastic and imperfection coefficients.

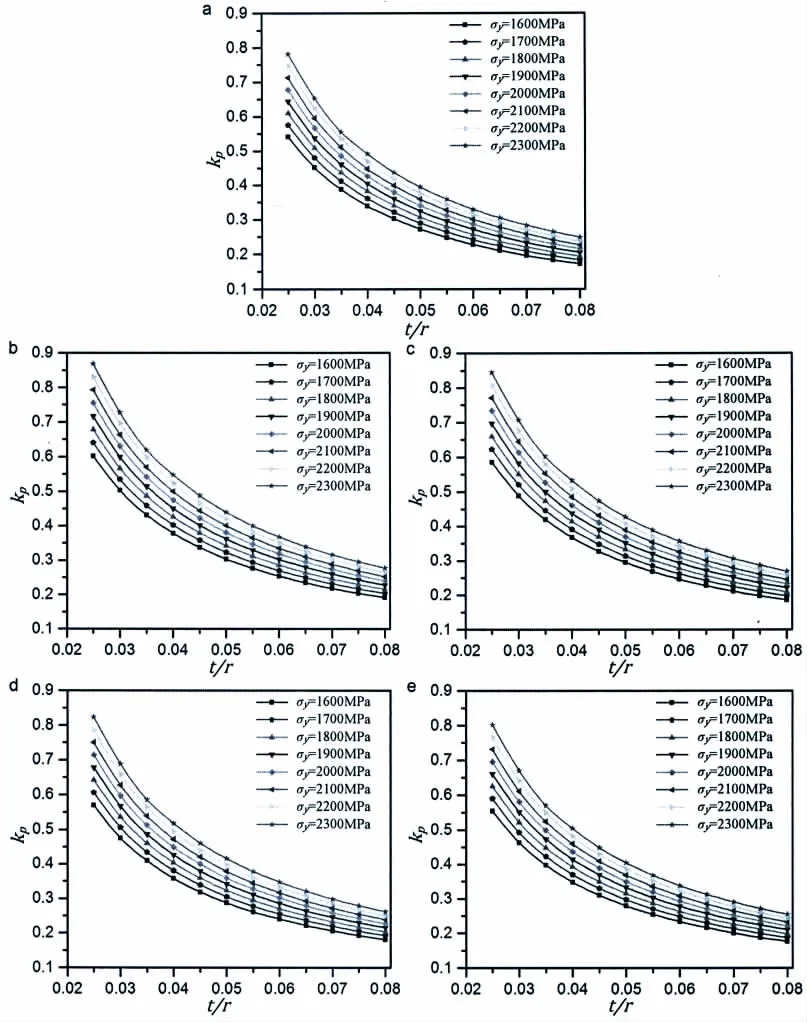
Fig.6 Plasticity reduction factor,kp,of maraging steel pressure hulls versus wall thickness-to-median radius ratio,η(a)E=200 GPa;(b)E=195 GPa;(c)E=190 GPa;(d)E=185 GPa;(e)E=180 GPa

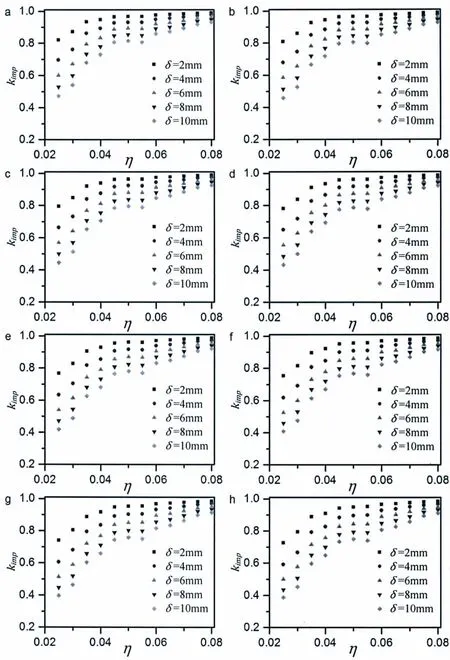
Fig.7 Imperfection reduction factor,kimp,of maraging steel pressure hulls versus wall thickness-tomedian radius ratio,η (a)σy=1 600 MPa;(b)σy=1 700 MPa;(c)σy=1 800 MPa;(d)σy=1 900 MPa;(e)σy=2 000 MPa;(f)σy=2 100 MPa;(g)σy=2 200 MPa;(h)σy=2 300 MPa

As can be seen from Eq.(10),Poisson’s ratio has a relatively small effect on the buckling load,which can be considered as a higher order infinitesimal.Besides,it varies very slightly in engineering application,the effect of Poisson’s ratio therefore can be neglected.However,Young’s modulus appears to greatly influence the buckling load due to the linear relation between them,which requires further study.Therefore,the effect of Young’s modulus on the plasticity reduction factor is evaluated by using GMNA.According to results of our pretest,the value of Young’s modulus is set to be 195 GPa,190 GPa,185 GPa,and 180 GPa,respectively.Poisson’s ratio μ=0.3,and yield strength σy=1 600-2 300 MPa with the increment of 100 MPa are assumed as well.In this way,a total of 96×4=384 numerical experiments are carried out.According to the obtained results(Fig.6),Eq.(11)can be rewritten as:

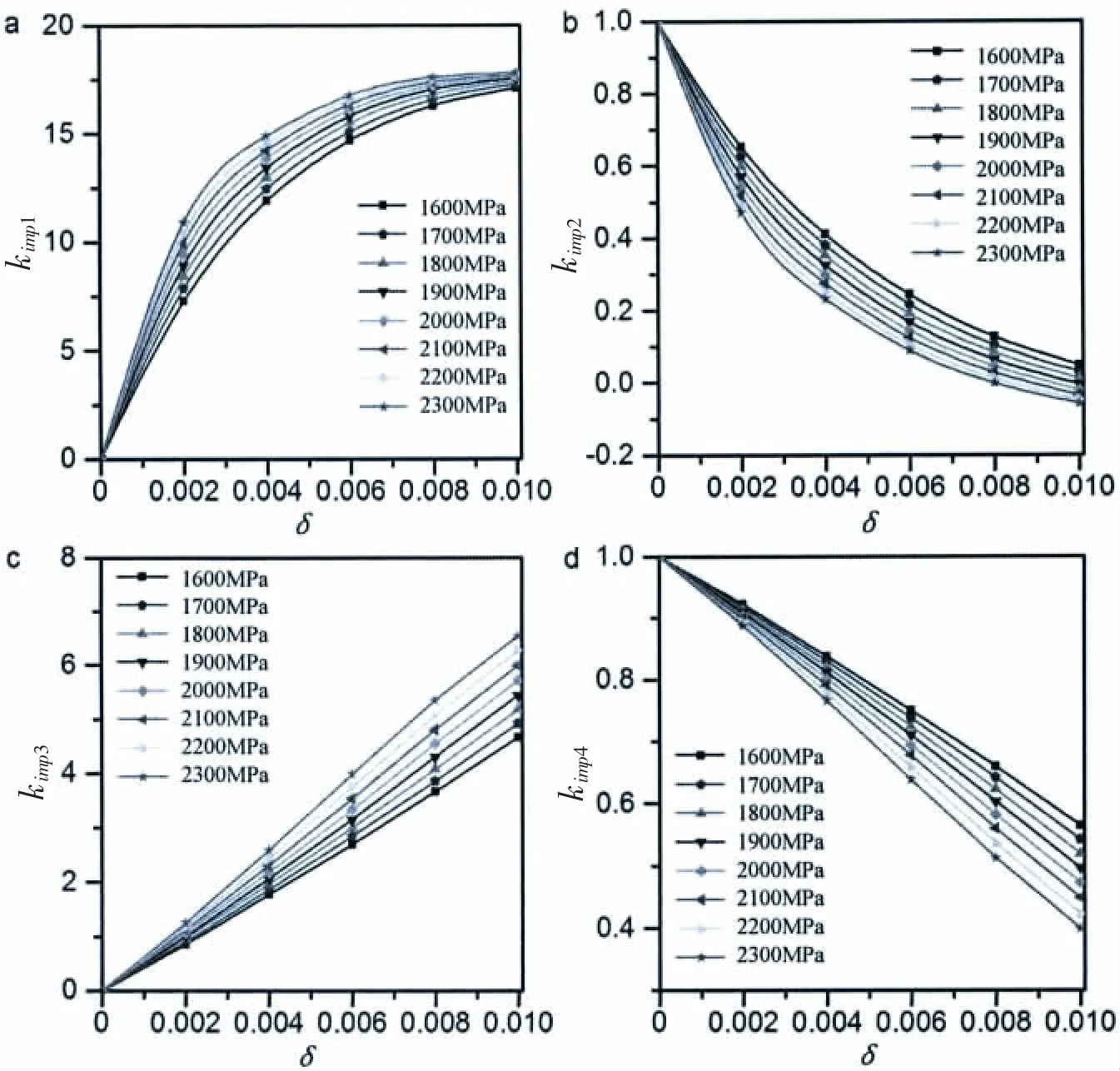
Fig.8 Imperfection coefficients,kimp1,kimp2,kimp3,and kimp4,of maraging steel pressure hulls versus the imperfection size-to-median radius ratio,δ,at yield strength,σy=1 600-2 300 MPa

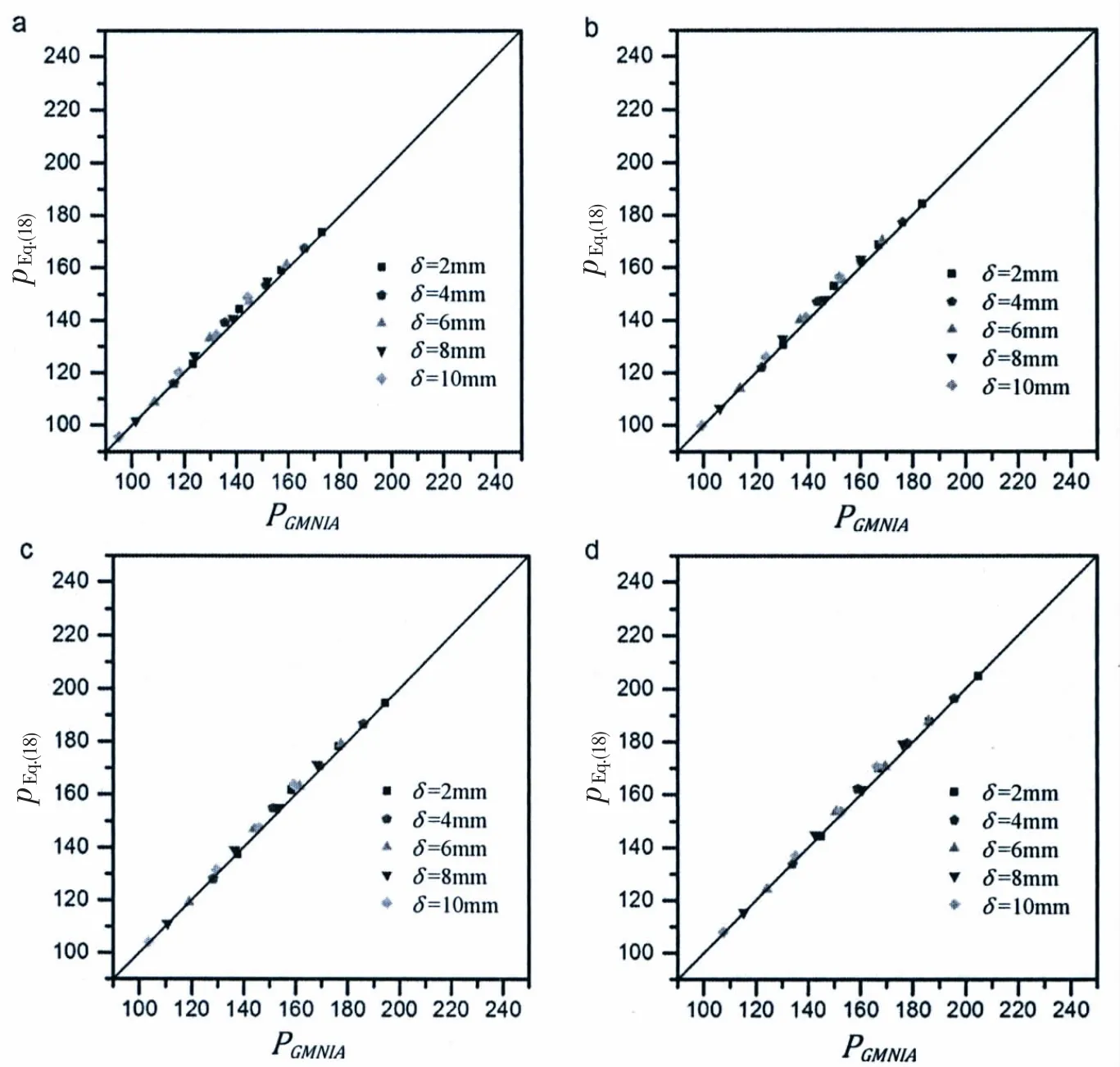
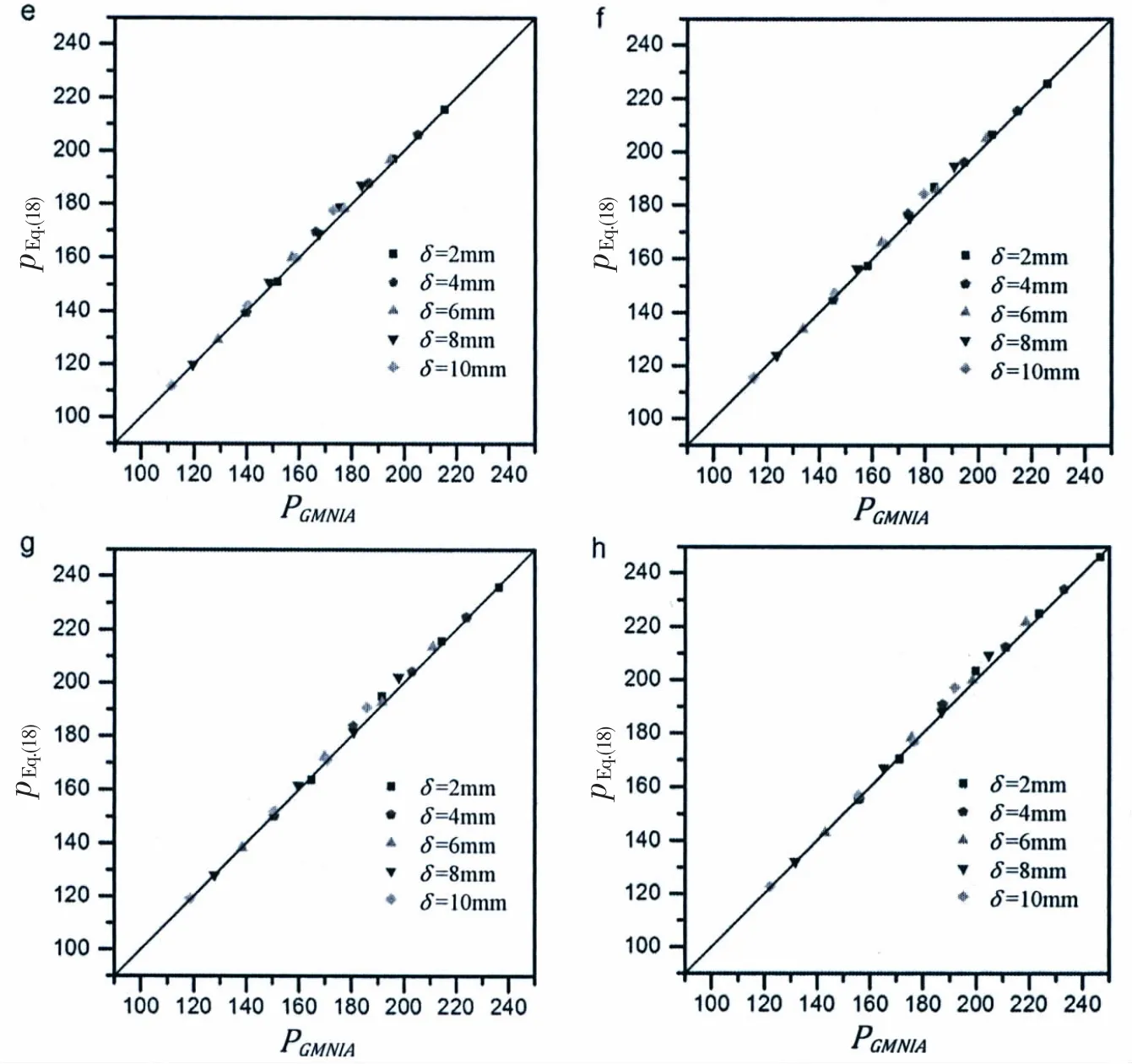
Fig.9 Buckling loads obtained from 480 geometrically and materially nonlinear analyses with imperfections included(GMNIA)versus the ones obtained from the proposed semi-analytical equation(Eq.(18))(a)σy=1 600 MPa;(b)σy=1 700 MPa;(c)σy=1 800 MPa;(d)σy=1 900 MPa;(e)σy=2 000 MPa;(f)σy=2 100 MPa;(g)σy=2 200 MPa;(h)σy=2 300 MPa

This modified equation(Eq.(20))indicates that Eq.(10)appears to yield relatively conservative results for deep maraging steel spherical pressure hulls,because the real plasticity reduction factor increases with a decrease in Young’s modulus,and Eq.(11)is deduced in the case of maximum value E=200 GPa.Therefore,combined Eq.(20)with Eq.(12)to respectively determine the plasticity reduction factor and the imperfection reduction factor,the modified semi-analytical formula to evaluate the nonlinear buckling load of deep maraging steel spherical pressure hulls may be given by:

To examine the accuracy of regression analysis and assure the design reliability of full ocean depth pressure hulls,a total of 288 buckling loads obtained from above GMNIA versus the ones obtained from Eq.(21)are plotted in Fig.9,which is done in the case of η=0.045-0.055,σy=1 600-2 300 MPa,and δ=0.002-0.008.As can be seen,most data points are either on or slightly above the diagonal line,the maximum difference between results obtained from two approaches is within 2%.This finding indicates that the proposed formula(Eq.(21))can yield a reasonable result when used to predict the nonlinear buckling loads of full ocean depth pressure hulls.

4 Evaluation of a full ocean depth pressure hull

The chapter conducts numerical and analytical studies into the strength,stiffness and stability of a deep maraging steel spherical pressure hull in a full ocean depth manned submersible.The hull has a median radius of r=1 000 mm,and a uniform wall thickness of t=50 mm,which is made from maraging steel with material properties as follows:Young’s modulus 180 GPa,Poisson’s ratio μ=0.3,yield strength σy=1 700 MPa.

4.1 Linear analysis

Two numerical models,including 2D-axi-symmetrical continuum model and 3D-shell structural model,are constructed and solved to obtain the strength of pressure hull.In both models,the material is defined to be purely elastic,and the geometry is assumed to be ideal without geometric imperfection.The numerical results are compared with analytical ones,as well.In the axi-symmetrical case,4-node bilinear element CAX4 is adopted with the total number of 4 707 nodes,which is sufficient enough to yield a convergence solution.To assure the safety of the pressure hull,the uniform pressure,p0=140 MPa,is selected as the design load and applied on the external surface of hull,which is even higher than the actual one(about 110 MPa)in full ocean depth environment.An inner point on the equator is constrained along the axis of symmetry to void rigid body motion and obtain radial displacements.Linear static analysis is carried out to determine the stress and displacement which indicates the linear elastic strength and stiffness of the hull.The numerical results are illustrated in Figs.(10-11).

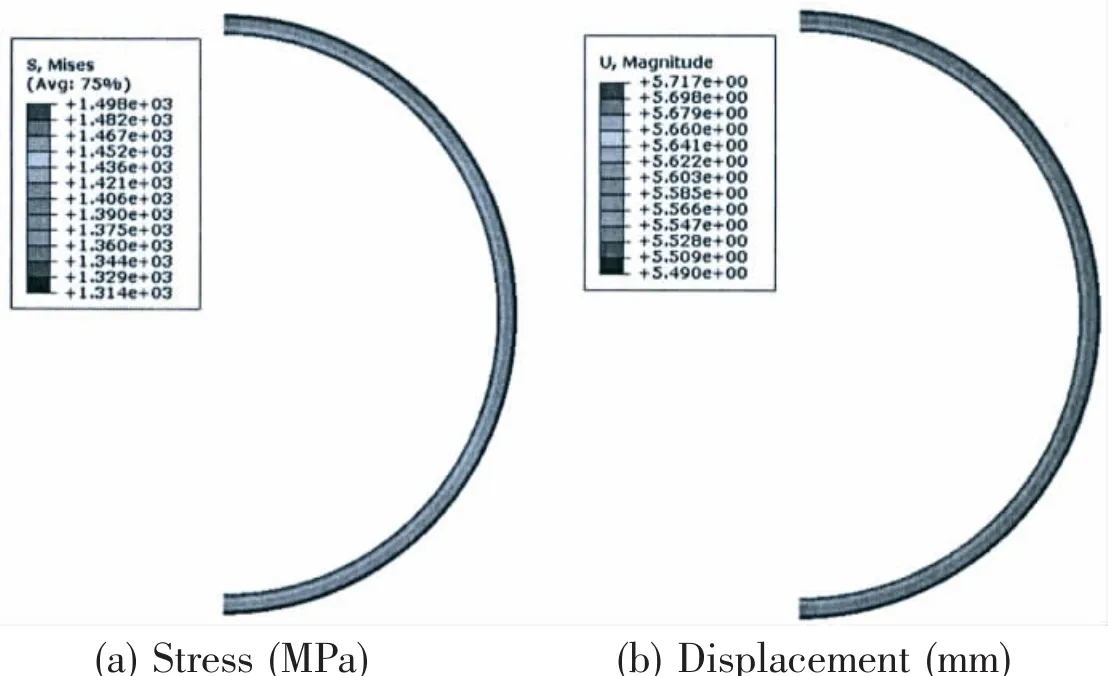
Fig.10 Stress and displacement distributions of the full-ocean-depth pressure hull subjected to 140 MPa uniform external pressure

Fig.11 Linear,critical and post buckling modes of the full-ocean-depth pressure hull

As can be seen,both stress and displacement are nearly identical in the meridional direction and strongly varied on the thickness due to the highly symmetric spherical configuration and the applied load.For example,the inner surface stress varies from 1 496.47 MPa to 1 497.56 MPa along the meridian with the average value of 1 497.02 MPa,which is only 0.68%lower than the analytical stress(1 507.33 MPa)obtained from Eq.(13).The outer surface stress varies from 1 313.61 MPa to 1 314.87 MPa along the meridian with the average value of 1 314.24 MPa,which is only 1.30%higher than the analytical stress(1 297.33 MPa)obtained from Eq.(14).These slight differences result from the assumption of finite element approximation.Both numerical and analytical results indicate that the strength of maraging steel spherical pressure hull far meets the design requirement because the yielding load(157.9 MPa)obtained from Eq.(15)is about 12%higher than the design load(140 MPa).Similarly,the average inner surface displacement(5.717 mm)is only 0.02 mm higher than the analytical one obtained from Eq.(18),whist the average outer surface displacement(5.490 mm)is the same as the analytical one obtained from Eq.(19).Both numerical and analytical results indicate relatively large deformation can be found for the pressure hull when diving into deep sea,which should be considered in the design stage to ensure deformation compatibility among components of the submersible.

On the other hand,in the 3D-shell structural case,the element type and number are the same as those of Section 3.1.The unit uniform pressure,p0=1 MPa,is applied on the external surface of hull.The boundary conditions are similar to Section 3.1.The subspace iteration method,suitable to analyze only a few eigenmodes,is implemented to obtain the first eigenvalue,which directly corresponds to the buckling load and indicates the linear elastic stability of the hull.The obtained buckling load is 537.18 MPa,which is 99.98%of the analytical solution(537.18 MPa,Eq.(16)).It is suggested that the stability appears to meet the design requirement in linear elastic range.However,the actual buckling load is ever lower than the linear buckling one due to the effect of geometric imperfections,material and geometry nonlinearities,which will be studied in the following section.In addition,the linear buckling mode takes the shape a number of circumferential and meridianal waves,which is typical for shells of revolution subjected to external pressure(Fig.11(a)).

4.2 Nonlinear buckling

Nonlinear numerical buckling analysis is carried out for the geometrically perfect and imperfect cases.The former case corresponds to geometrically and materially nonlinear analysis(GMNA)as well as zero imperfection size of imperfect case,whilst the latter case corresponds to geometrically and materially nonlinear analysis with the first eigenmode imperfections included(GMNIA).The mesh,load,boundary condition,material modeling,imperfection definition and analyzing method are nearly the same as those of Section 3.1.In addition,nonlinear buckling loads are also solved using the proposed semi-analytical formula(Eq.(21)).Taking the 2 mm imperfection size as an example,detailed solving flowchart is given in the following steps:

Step(1)is to determine the linear elastic buckling load,pm-t,according to Eq.(16),as follows:

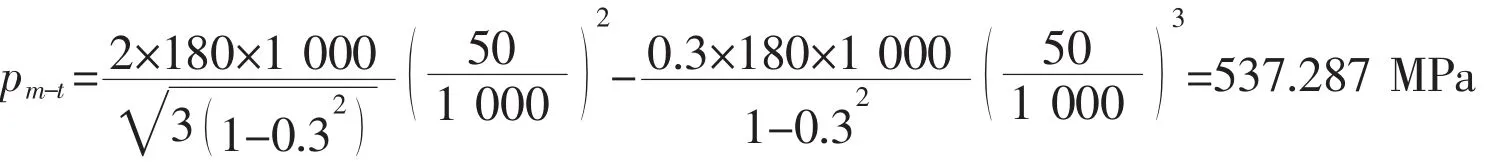
Step(2)is to determine the plasticity reduction factor,kp-modify,according to Eq.(20),as follows:

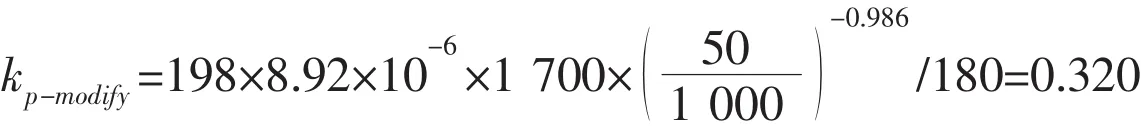
Step(3)is to determine the imperfection reduction factor,kimp,according to Eq.(12),as follows:

(1)The imperfection coefficients according to Fig.8(a-b)are determined as:kimp1=7.850 and kimp2=0.626;

(2)The imperfection coefficients according to Fig.8(c-d)are determined as:kimp3=0.966 and kimp4=0.911;

(3)Then kimp=(0.045×7.850+0.055×0.966+0.626+0.911)/2=0.971.

Note:in the case of the geometrically perfect case,one can assume kimp=0;when the geometry,material and imperfection parameters of spherical pressure hulls do not correspond to the numerical data,one can obtain the imperfection coefficients using the linear mapping method in Fig.8.

Step(4)is to determine the nonlinear buckling load,pu-modify,according to Eq.(21),as follows:

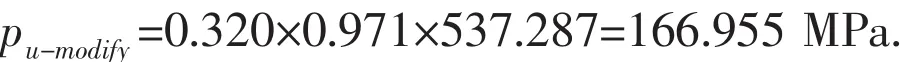
Tab.1 shows the results obtained from numerical and semi-analytical analysis.As can be seen,both nonlinear numerical and semi-analytical buckling loads decrease significantly compared with the linear buckling results,due to the effect of material plasticity and geometric imperfections on the buckling.This obvious decrease confirms previous studies that theoretical linear buckling load of a spherical shell cannot match with the experimental one(Lee et al,2016)[15],which indicates that nonlinear plastic buckling analysis of imperfect geometry should be performed to evaluate its load-carrying capacity.The nonlinear buckling load decreases with an increase in the imperfection size,confirming that spherical shells are imperfection-sensitive structure.It indicates that the maximum imperfection size caused by fabrication may not exceed 8 mm because the nonlinear buckling load at this size is slightly higher than the design load(140 MPa).Also,good agreement can be obtained between nonlinear numerical and semi-analytical results,as the ratio of nonlinear numerical to semi-analytical loads varies from 0.99-1.02.

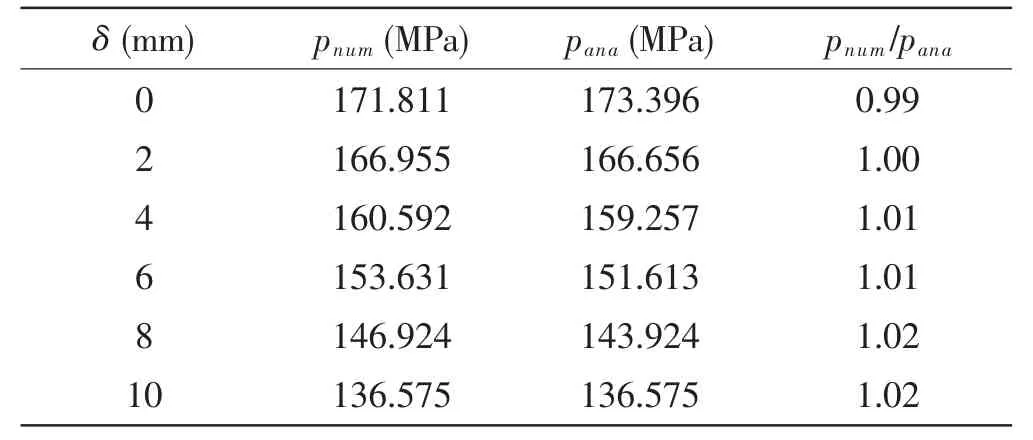
Tab.1 Nonlinear numerical,pnum,and semianalytical,pana,buckling loads at various imperfection size,δ

In addition,the equilibrium paths,critical and post buckling modes of imperfect hulls obtained from numerical analysis are similar and typical for shells of revolution under external pressure.For example,the numerical results of the spherical pressure hull with 6 mm imperfection size are illustrated in Fig.12.Its equilibrium path,providing the applied pressure,p,versus the maximum deflection,u,normalized by its wall thickness,t,has an unstable character resembling a parabola.The critical buckling mode at the peak of the path is consistent with the linear buckling mode mentioned in Section 4.1.The post buckling mode at the end of the path takes the shape of a local dimple,which is consistent with results in previous studies(Blachut,2013[5];Zhang et al,2017[14]).

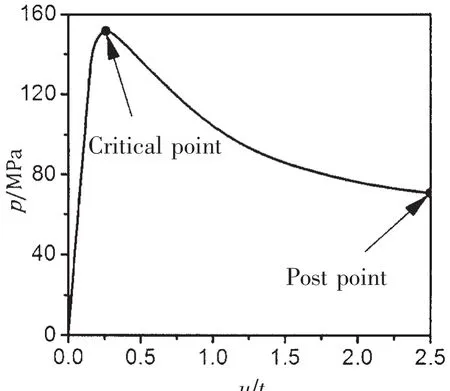
Fig.12 Equilibrium path of the spherical pressure hull at 6 mm imperfection size

5 Experimentation

Fig.13 Diagram of hemi-spherical shell(a)and fabricated prototype(b)

A model of hemi-spherical shell is tested to destruction in a cylindrical pressure chamber locating at Shanghai Engineering Research Center of Hadal Science and Technology,Shanghai Ocean University.Consider a hemi-spherical shell with radius,r,and uniform wall thickness,t,under uniform external pressure,p,shown in Fig.13.On the base of the shell,there is a heavy ring with height,h,external diameter,D,and internal diameter,2r,which is welded to a heavy plate with height,H,and diameter,D.Such constrain can result in a fixed boundary condition for the shell.The shell,ring,and plate are made of maraging steel,which demonstrates extremely high yield strength.The material properties are provided by the Shanghai Jiao Tong University as follows:Young’s modulus E=182 GPa;Poisson’s ratio μ=0.303;Yield strength σy=2 100 MPa.The stress-strain curve can be seen form Fig.14.All the important geometry parameters and material properties are listed in Tab.2.The collapse pressure of the tested hemi-spherical shell,corresponding to the maximum recorded value in Fig.15,is as much as 139 MPa.The numerical result(131.214 MPa)obtained from Eq.(21)is just 5.6%lower than the test result.In addition,it is conservative to preliminary design.

Tab.2 Geometry parameters and material properties of fabricated hemi-spherical shell

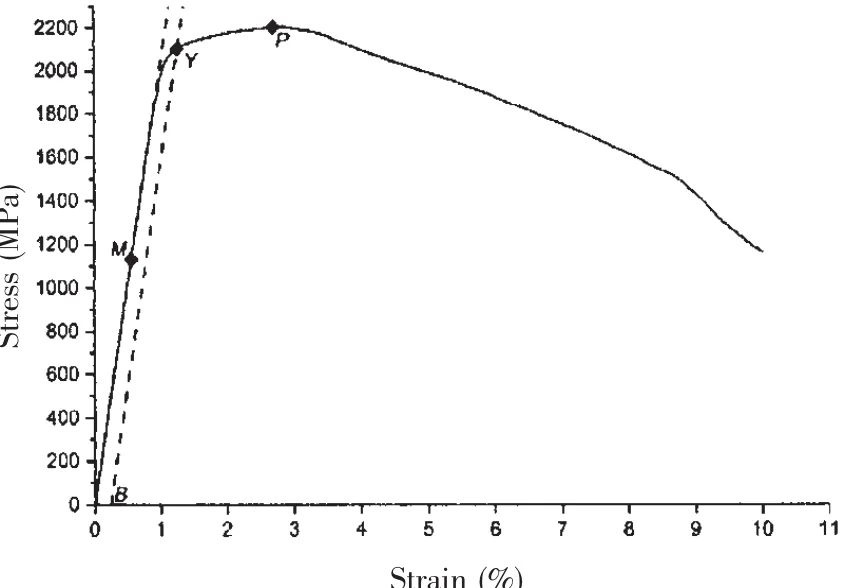
Fig.14 The stress-strain curve of maraging steel

Fig.15 Applied pressure versus time

6 Conclusions

(1)A set of numerical experiments concerning the nonlinear buckling are carried out to obtain the nonlinear buckling loads of deep maraging steel spherical pressure hulls under various wall thicknesses,imperfection sizes,yield strengths,and Young’s modulus.Spherical pressure hulls considered have a median radius of r=1 000 mm,a uniform wall thickness of t=25-80 mm with the increment of 5 mm.Referring to the pretest of maraging steel,it is assumed that the material properties are as follows:Young’s modulus E=200 GPa,Poisson’s ratio μ=0.3,yield strength σy=1 600-2 300 MPa with the increment of 100 MPa.Based on the numerical results and shell theory,a semi-analytical formula,including the plasticity reduction factor,the imperfection reduction factor,and the analytical linear elastic buckling load of thick-walled shells,is tentatively deduced and reasonably benchmarked.This formula,including the effect of Young’s modulus,extends previous studies regarding the formula to predict the nonlinear buckling load of titanium alloy spherical pressure hulls.

(2)The strength characteristics of a deep maraging steel spherical pressure hull in a full ocean depth manned submersible are systematically studied as an example using numerical method,which are compared well with analytical or semi-analytical results.This finding suggests that the proposed analytical formulae can be used to examine the linear elastic strength,stability,and stiffness of deep spherical pressure hulls,whist the proposed semi-analytical formula can be used to examine their nonlinear buckling loads.In addition,a model of hemispherical hull is tested in the Shanghai Engineering Research Center of Hadal Science and Technology and the analytical result obtained from Eq.(21)is just 5.6%lower than the test result.These formulae may play a key role in developing the next generation design rules of deep manned pressure hulls.Nevertheless,the current work only focuses on the first eigenmode im-perfection,other imperfections resembling local dimple,axisymmetric dimple,higher eigenmodes and their combinations should be studied in future.

Acknowledgments

This work was supported by the Key Program of National Natural Science of China(Grant No.51439004)and the General Program of National Natural Science Foundation of China(Grant No.51679133 and 51709132).The authors would like to express their gratefulness to the three anonymous reviewers whose constructive comments significantly improved this paper.