江 青 宇

(复旦大学计算机科学技术学院 上海 200433)

0 引 言

对于G=(V,E)表示的一个无向连通图，集合V是其所有顶点的集合，集合E是其所有边的集合。图G的一个匹配M是边集合E的一个子集，且在M中任意两条边都互不相邻，即M中没有两条边连接在一个相同的顶点上。一个顶点如果被匹配M中的一条边连接，我们称这个顶点被匹配M覆盖。若图G中没有不同于M且所包含边的数量多于M的匹配M′，就称匹配M为图G的一个最大匹配。匹配中两种比较特殊的情况为：若图G中的所有的顶点都被匹配M覆盖，匹配M称为图G的一个完美匹配；若图G中除一个顶点外的其余所有顶点都被匹配M覆盖，匹配M称为图G的一个近完美匹配。图G的最大匹配包含的边数称为图G的匹配数。

复杂网络上一类很重要的问题就是复杂网络上的计数问题[1]。复杂网络上计数问题在很多领域都有着广泛的应用，其中比较典型的就是网络的匹配问题[2]。例如网络匹配数和最大匹配的数目经常被用在化学[3]中。研究发现，在顶点[4]或者边[5]动力学性质的基础上，最大匹配数和最小支配集是复杂网络结构可控性分析的重要工具[6]。在点动力学的背景下，控制整个网络最少驱动顶点的数目和驱动顶点集合可能的配置，分别由原始网络派生出一个二分图的匹配数和最大匹配的数目决定[4]。然而，在一般图中求解最大匹配数是很困难的，甚至在二分图上都是一个NP完全问题[7]。在目前，复杂网络上的匹配问题仍然是科研人员积极研究的内容[8]。

由于寻找网络所有的匹配，特别是在一般图上是难以做到的，因此本文对那些既在现实网络中有重要意义，又能够对网络上的匹配问题进行求解的图给予了更多的关注[9]。在复杂网络的研究中，Sierpiński网络是一类有着重要研究意义的网络[10]。本文研究的无标度Sierpiński网络可以更方便地研究一些真实网络系统的复杂性，并且其具有更广泛的适用性。例如，其可以运用于调查城市导航的复杂性[11]；被频繁地用于RNA折叠研究[12]；可被应用于调查旅行商问题的复杂性[14]。而且，将无标度Sierpiński网络与聚合物相联系起来已被证明对于高分子物理的研究有很大帮助[13]。

针对以上问题，无标度Sierpiński网络的相关拓扑性质的研究还是空白。本文主要研究无标度Sierpiński网络上的匹配问题，包括无标度Sierpiński网络的匹配数、边覆盖数、最大匹配的数目。本文利用无标度Sierpinski的自相似性，计算出了无标度Sierpinski网络的匹配数。利用网络的边覆盖数和匹配之间的关系，给出了无标度Sierpinski网络的边覆盖数的解析式。通过对无标度Sierpinski网络匹配的类型进行分类，分析不同情况下匹配数目最大的情况下可能的网络构造方式，根据网络迭代次数的奇偶性给出了最大匹配数目的递推表达式。

1 网络构造与性质

1.1 网络的构造

对于第n代无标度Sierpiński网络，当n=0时，无标度Sierpiński网络I0为一个三个顶点构成的三角形，当n≥1时，记网络最外层的3个顶点分别为A、B、C，那么无标度Sierpiński可由下面的过程来迭代构造：

(1) 将3个无标度Sierpiński网络In-1，分别命名为In-1(i)，i=1,2,3,每个无标度Sierpiński网络In-1的最外层3个顶点命名为Ai、Bi、Ci(i=1,2,3)，其中Ai、Bi、Ci分别对应In-1(i)中的顶点A、B、C。

(2) 将A1和A3(或者B1和B2，C2和C3)合并为产生无标度Sierpiński网络In的最外层顶点A(或者B,C)，而A2、B3、C1之间分别两两相连形成In中心的三角形。

图1表示了这样的构造过程。从上面的构造方法可以知道，当n≥1时，第n代无标度Sierpiński网络In可以看成由三个前一代的无标度Sierpiński网络In-1构造而来，因而无标度Sierpiński网络有很好的自相似性。

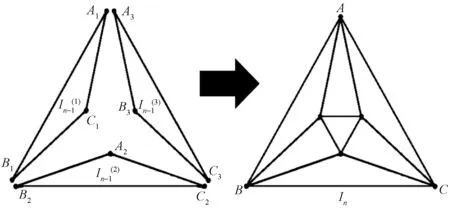
图1 无标度Sierpinski网络的构造方法

1.2 网络的性质

令Vn和En分别表示第n代无标度Sierpiński网络的总顶点数和总边数，从上面的构造方法容易得出以下关系：

Vn=3Vn-1-3

En=3En-1+3

解出步骤n中存在的顶点Vn和边En的总数分别是：

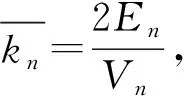
文献[15]给出了每一代无标度Sierpiński网络的度分布Pcum(k)。通过每一次构造时的规律，得出原来顶点和新产生顶点的度，进而求得整个网络In的度分布：

当n趋向于无穷大时，可以得到：

Pcum(k)=(k-2)-(ln3/ln2)

与很多现实网络一样，无标度Sierpiński网络的度分布指数也满足幂率分布。

2 无标度Sierpiński网络的匹配

2.1 匹配数目

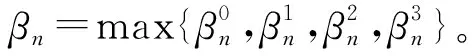
定理2对于两个相邻阶的无标度Sierpiński网络In和In+1(n>1)，下面的关系式成立：

图2 In+1中所有中的匹配的布局

定理4无标度Sierpiński网络In(n≥2)的匹配数为：

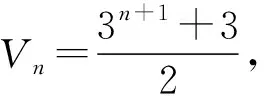
2.2 边覆盖数

边覆盖是一类边的子集。对于无向连通图G=(V,E)，集合V是其所有顶点的集合，集合E是其所有边的集合。若E′⊆E，即图G的每一个顶点在E′中都有边与之关联，那么称E′为图G的边覆盖集，简称边覆盖。在所有边覆盖中，包含边数最少的边覆盖称为最小边覆盖，其所包含的边数称为边覆盖数。对于连通网络上，最大匹配数与最小边覆盖数之和等于网络顶点数。根据两者之间的关系，结合上文求解到的匹配数，可以很容易地求出无标度Sierpiński网络的边覆盖数。

定理5无标度Sierpiński网络In的边覆盖数为：

定理5给出无标度Sierpiński网络的边覆盖数，由于当n是偶数时，结点数目为奇数无标度Sierpiński网络存在近完美匹配，因此只需在最大匹配的基础上增加一条边覆盖唯一不在最大匹配中的顶点。当n是奇数时无标度Sierpiński网络存在完美匹配，最大匹配数即为边覆盖数。

2.3 最大匹配的数目

令τn为无标度Sierpiński网络In最大匹配的数目。为了求解τn，本文引入了三个辅助的量。令φn为无标度Sierpiński网络In的最外层3个结点X、Y、Z均未覆盖的最大匹配的数目。令θn为无标度Sierpiński网络In覆盖了顶点Z而未覆盖顶点X、Y的最大匹配的数目，同时它也等于无标度Sierpiński网络In覆盖了顶点X而未覆盖顶点Y、Z的最大匹配的数目，和无标度Sierpiński网络In覆盖了顶点Y而未覆盖顶点X、Z的最大匹配的数目。令φn为无标度Sierpiński网络In覆盖了顶点X、Y而未覆盖顶点Z的最大匹配的数目，同时它也等于无标度Sierpiński网络In覆盖了顶点Y、Z而未覆盖顶点X的最大匹配的数目，和无标度Sierpiński网络In覆盖了顶点X、Z而未覆盖顶点Y的最大匹配的数目。对于比较小的n，φn、θn、φn、τn都比较容易求解。例如，当n=2时，φn=8、θn=112、φn=56、τn=1 392。但当n继续增大时，直接求解是比较困难的，所以本文给出了无标度Sierpiński网络最大匹配的数目的递推关系式。

定理6对于无标度Sierpiński网络In，φn、θn、φn、τn可以依据下式递推地表示，当n为奇数时：

当n为偶数时：

证明：在文中仅证明当n为偶数时的第一个等式。

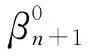
从定理6可以看出，无标度Sierpiński网络随着结点总数奇偶不断变化，最大匹配的组合情况也在不断改变。

3 结 语

本文求解了无标度Sierpiński网络的匹配数，利用无标度Sierpiński网络结构上的规律，建立了匹配数的递推关系，最后得到了匹配数的解析表达式，避免一般求解匹配数方法的高时间和空间复杂度。随着无标度Sierpiński网络每一次的迭代构建，网络的结点总数也在奇偶交替变换，且当网络结点总数为偶数时，无标度Sierpiński网络存在完美匹配，边覆盖数等于匹配数；当网络结点总数为奇数时，无标度Sierpiński网络存在近完美匹配，边覆盖数等于匹配数加1。本文计算出匹配数最大时可能出现的子图的组合情况，然后结合无标度Sierpiński网络的结构特点，建立每种情况最大匹配数的递推关系，最后得到了无标度Sierpiński网络最大匹配数的递推关系式。本文采用的方法，不仅对无标度Sierpiński网络适用，对其他有自相似性质网络上的计数问题也有重要的借鉴意义。