江 峰，倪少权*,b,c，吕红霞,b,c

(西南交通大学a.交通运输与物流学院;b.全国铁路列车运行图编制研发培训中心;c.综合交通运输智能化国家地方联合工程实验室,成都610031)

0 引言

列车运行图调整是根据运输需求完善运行图的过程，分局部调整与全局调整.局部调整在既有框架下根据增开列车需求增铺运行线，涉及新增运行线铺画和既有运行线调整；全局调整则是全图运行线的重新铺画.既有高速铁路运行图框架是列车开行方案长期优化的结果，通常不进行全局调整.随着路网完善及运输需求变化，高速铁路运行图局部调整增多，现有的人工推线求解方法难以保证质量，存在很大局限性，因此有必要研究列车运行图局部调整模型与算法.

列车运行图调整属列车运行图编制(Train Timetabling Problem,TTP)范畴，是 NP-hard问题[1-3]，大量国内外学者对相关问题进行了研究.国内方面，文献[2]以单线区段为背景，优化各运行线旅行速度.文献[4]构造了适用于单双线区段的运行图时空窗口，滚动求解各运行线.文献[5]考虑上下行列车到发站属性差异，求解单线非追踪平行运行图最小周期.文献[6]在周期性运行图基础上，以深度搜索法添加非周期运行线.文献[7]总结了基于周期事件规划问题(PESP)的周期性运行图模型及其应用情况.其中文献[4,6]属启发式方法，缺乏对所得解的优劣评价；文献[2,5]研究单线区段，不完全适用于高速铁路双线区段；文献[6-7]研究对象为周期性运行图.国外方面，文献[3]通过给定各列车初始利润，以总收益最大化为目标建立整数规划模型，对原模型进行拉格朗日松弛，以动态规划方法求解各运行线.文献[1]根据给定列车开行方案，基于时空网络铺画周期性运行图.文献[8]以路网中列车总旅行时间最小为目标，研究货物列车最优径路问题.上述研究基于拉格朗日松弛技术，适用于周期[1]及非周期列车运行图[7-8]，并能有效评价所得解的优化程度[1,7-8].文献[9]归纳总结了不同运行图编制模型的特点及适用情况.

上述研究为本文奠定了理论基础.我国高速铁路运行图呈非周期性，局部调整以新增列车开行方案为基本输入，需调整的既有运行线可视为一类特殊的新增列车，从而将局部调整转化为给定框架下的新增运行线求解问题.现有基于拉格朗日松弛的运行图调整模型简化了列车在区间运行状态，未考虑停站引起的起停车附加时分[7-9]，无法实际应用.本文在文献[1,7-8]的基础上，考虑列车停站需求，细化停站对列车区间运行时分的影响，给定各新增列车一个由理想始发时刻及始发时刻可调整度、全程停时总延长决定的始发时间域，将运行线铺画转化为最短路求解问题，建立整数规划模型并进行拉格朗日松弛求解，根据对偶信息设计启发式算法迭代求解运行图最优可行解.

1 问题描述

运行图可由有向时空网络描述[1,7-9]，其中纵轴表示车站、横轴表示时间.将1天以分钟为单位离散为1～q，每个车站包含1 440个节点，每条列车运行线所经节点即可由车站及所经节点对应时刻确定.以G=(N,A)表示该有向时空网络，其中点集N中元素代表时空域上车站所在位置，包括到达节点U及出发节点W；弧集A中元素代表相邻节点间有向弧，为列车运行线组成部分.对每条运行线设置一个虚拟出发点σj及虚拟终到点εj，则有N=

设S为全体车站集合，给定列车集以表示列车j∈T所经车站集合(共s站).运行图局部调整即为在G=(N,A)中，在原有框架下，根据给定新增列车始发时间域铺画新增运行线的过程，如图1所示，其中T1为新增列车.

上述问题为一定约束下G中自fj起，途径fj+1,…,lj-1至lj止的最短路径，可表示为，其中Nj,j∈T表示列车j所经车站节点构成的点子集，由列车j所经车站及在该站的到达、出发时刻决定；Aj,j∈T表示与列车j有关的弧子集，由列车j的区间运行时分或在站停时决定，其中的求解范围由列车始发时间域及全程停时总延长范围决定.列车j的运行线即为与其有关的弧子集Aj中的元素，包含有：从虚拟出发点σj至列车j始发站出发节点v∈Wfj的始发弧；在中间站，由到达节点u∈Ui至出发节点v∈Wi的停留弧；由车站i至i+1区间内经由车站i出发节点v∈Wi至车站i+1到达节点u∈Ui+1的运行弧(v,u)；从列车j终点站到达节点u∈Ulj至虚拟终到点εj的终止弧(u,ε).其中，在站停留弧(u,v)的占用时间为列车j在车站i的停站时间，当列车在站通过不停车时，其占用时间为0；运行弧(v,u)的占用时间为列车j在区间(i,i+1)的总运行时分，由列车区间运行时分决定.

2 列车运行图局部调整模型

2.1 变量说明

2.2 模型约束

新增运行线j需满足一定约束.对两相邻列车j、k而言，在任意站，其构成弧需满足车站间隔约束、运行线唯一性约束、列车停站约束及相关连接变量约束等.

2.2.1 车站间隔约束

(1)列车在车站i的出发时刻应不小于该站发车间隔di，即Δ(v1,v2)≥di,v1＜v2，如图2所示.

图2 发车间隔示意图Fig.2 Departure interval

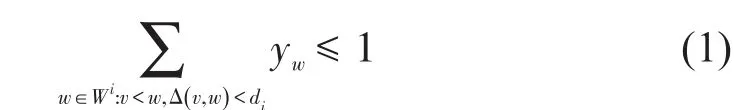
(2)列车在车站i+1的到达时刻应不小于该站到达间隔ai+1，即Δ(u1,u2)≥ai+1,u1＜u2，如图3所示.

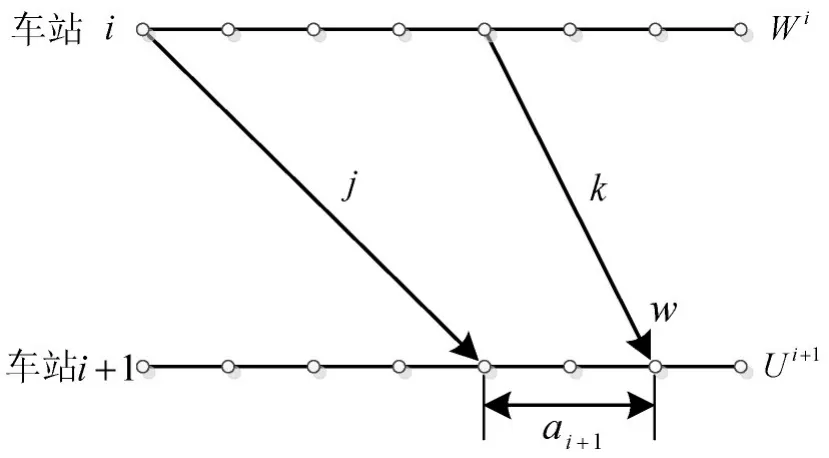
图3 到达间隔示意图Fig.3 Arrival interval

约束可表示为对任意i∈S/{1},u∈Ui+1，在Δ(u1,u2)＜ai+1内所有节点u至多有1个被某运行线经过，即

(3)两运行线在区间内不相交，设v1＜v2,u2＜u1，如图4所示.

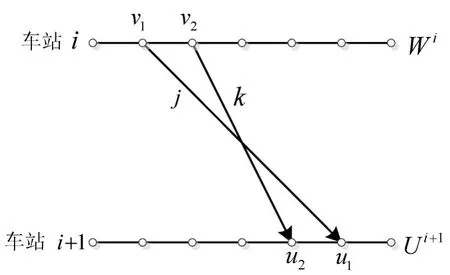
图4 区间不相交约束示意图Fig.4 No overpass in sector constraint

设区间内列车k的速度高于列车j，约束可表示为对任意相邻车站i和i+1，运行线j、k，图4所示的4个节点中，至多3个被这两条运行线经过，设v1＜v＜v2，u2＜u＜u1，有

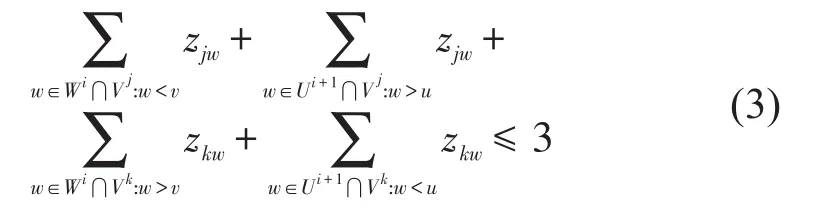
2.2.2 运行线唯一性约束

(4)始发弧数量约束.

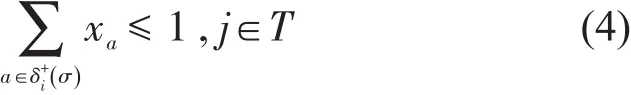
(5)节点v进入、离开弧数量约束.

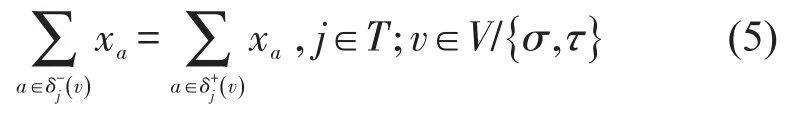
(6)节点v选择次数约束.

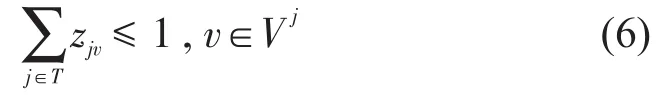
2.2.3 列车停站约束

列车停站约束为列车j在经停站停时不少于该站计划停时；在非经停站出发时刻与到达时刻相等.设θ(v)=θ(u)+tij,i∈Scj⊆Sj,j∈T，Scj为列车j的经停站，tij为列车j在车站i的计划停时，包括：

(7)经停站出发时刻选择限制.

(8)非经停站出发时刻选择限制.

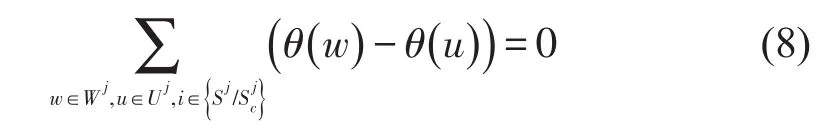
2.2.4 连接变量约束

连接变量约束为各0-1变量间相互约束.

(9)弧构成约束.

(10)节点选择约束.

2.3 目标函数

各运行线始发时间域及总停时限制决定了其所有可选节点及弧的子图Gj=(Nj,Aj)，其可行解即为在Gj=(Nj,Aj)中满足上述约束条件的1条路径.为评价解的质量，对每一条运行线j初始点赋予初始利润πj，对其相对计划始发时刻的调整及总停时延长赋予罚数，该运行线的最终利润即为各构成弧的利润之和[1].

设αj、βj为相应系数，对每个初始弧(σ,v),v∈Wfj，设υ(v)为始发点v对应时刻与理想始发时刻θ(fj)的差值，有其利润为p(σ,v)=πj-αjυ(v)；对每一个停留弧(u,v),u∈Ui,v∈Wi,i∈Sj/{fj,lj}，设μ(u,v)为实际停时与计划停时θ(u,v)的差值，其利润为p(u,v)=-βjμ(u,v)，以pa表示运行线j中所有弧a∈Aj利润之和，有pa=p(σ,v)+p(u,v)，以全图所有运行线利润最大构建目标函数[1].

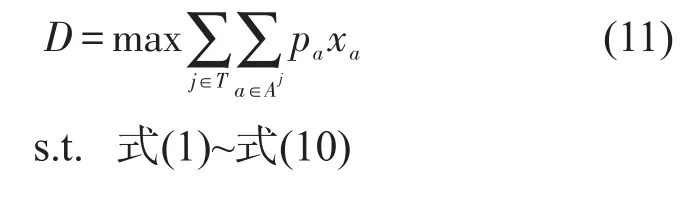
3 基于拉格朗日松弛的启发式算法

3.1 约束松弛

上述模型中行车组织约束属于簇约束，数量随问题规模快速增长，会引起模型规模的急剧扩大，对其进行拉格朗日松弛可加快求解速度[1,8-9].基于文献[1,8-9]所述方法，对原模型中式(1)～式(3)分别增加拉格朗日乘子后添加至目标函数，将其转化为

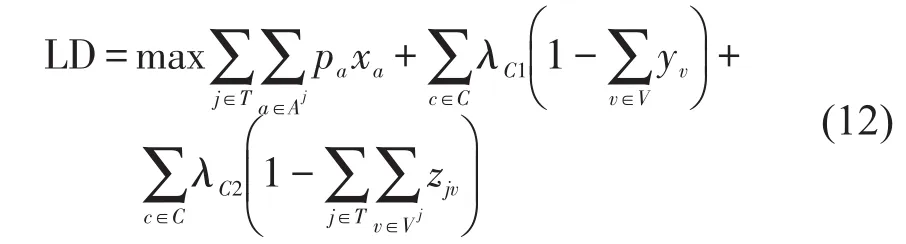
式中：C——由行车组织约束决定的与该节点不相容弧集[10]；

λC1、λC2——对应的拉格朗日乘子.

对式(11)进行恒等变换，即

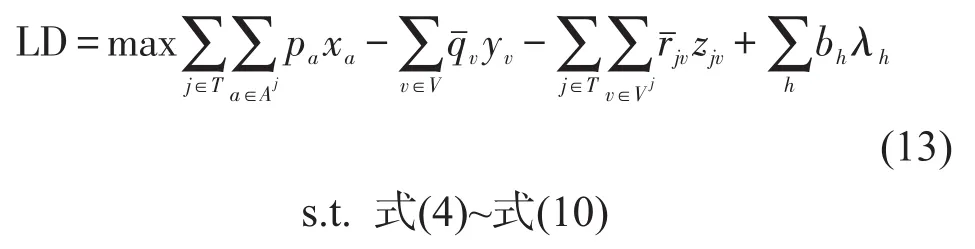
λh——第h个松弛约束对应的拉格朗日乘子，其含义为，①当λh对应约束为式(1)或式(2)，即yw时，有bh=1，任何经过点w的运行线将被赋予1个罚数λh.②当λh对应约束为式(3)，即zjw时，有bh=3，任何经过点w的列车j将被赋予1个罚数λh.

原模型松弛后，各运行线间约束关系被弱化，可由线性规划方法快速求解[1,7,10]，所得结果即为各运行线的拉格朗日松弛解.

3.2 可行解启发式求解

由于松弛了原模型中部分约束，LD中各运行线拉格朗日松弛解可能是实际非可行解.为求得实际可行解FD，设计下述启发式算法：

(2)新增运行线按拉格朗日松弛解利润大小排序确定铺画顺序.

(3)在新增运行线始发时间域内基于所有可行出发节点并考虑p(σ,v)、p(u,v)，选择λh(N)=0的节点，以min(p(σ,v)+p(u,v))为目标，基于深度搜索算法[5]求解实际利润最大的运行线，并记录每个车站的最大停留列车数，若大于该站到发线数量，则该运行线无实际可行解，所得解为各运行线的实际可行解.

(4)求解全图实际利润大于零的运行线实际利润之和，结果记录为FD的解.

所求得的FD为D的1个实际可行解[5,10].由于考虑了λh(N)=0的限制，因此有FD≤D，即FD为D的1个下界.

3.3 拉格朗日乘子更新

由于FD≤D≤LD，故D最优解处于区间(FD,LD)内，通过更新拉格朗日乘子，可优化FD的目标函数值，使其趋近于D最优解[7-10].拉格朗日乘子的更新由LD中式(1)～式(3)的违反情况确定[10,11]，其步骤为：

(1)初始化各约束次梯度要素viol(λh)=-1.

(2)对各运行线构成弧检查是否满足第h个约束条件，若违反该约束则对第h个约束的次梯度要素更新为viol(λh)=viol(λh)+1.

(4)根据Fisher提出的式(15)更新第h个约束对应的拉格朗日乘子λh[10-11].

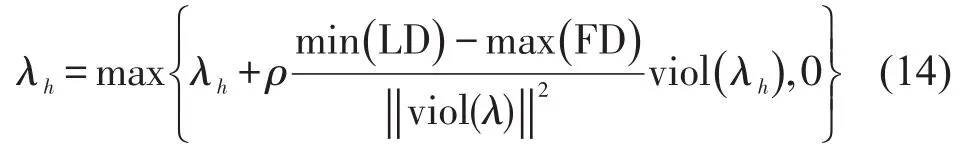
式中：ρ——给定的非负步长[10-11]，初始值设为ρ=1，当迭代10次min(LD)未发生改变则减半ρ取值.

通过上述过程可优化LD及FD的目标函数值，从而对FD进行迭代优化，当LD与FD满足一定条件时可认为已求得最优可行解[1,7-10].

3.4 算法流程

Step 0初始化，记录起始时间，设迭代次数为0，当前最优可行解为0，当前最优上界为全图各运行线初始利润之和.

Step 1求解LD，记录当前最优上界为min(LD).

Step 2根据LD所得各节点罚数λh(N)，以3.2节所述方法求解运行线实际可行解，计算全图各运行线实际可行解利润和FD，记录当前最优下界为max(F D).

Step 3设gap=(min(LD)-max(FD))/max(FD)⋅100%，判断max(FD)与min(LD)间差值是否小于设定gap值，若是，算法终止，最优下界所对应的解即为最优可行解；若否，迭代次数+1，转Step4.

Step 4以3.3节所述方法更新拉格朗日乘子λh.

Step 5检查算法运行时间、迭代次数是否达到设定最大值，若是，算法终止，最优下界对应解即为最优可行解；若否，转Step1.

4 算例验证

以2015年5月京沪高铁运行图为例，在原图302条运行线框架下增铺24条G类高速运行线，新增列车信息如表1所示.

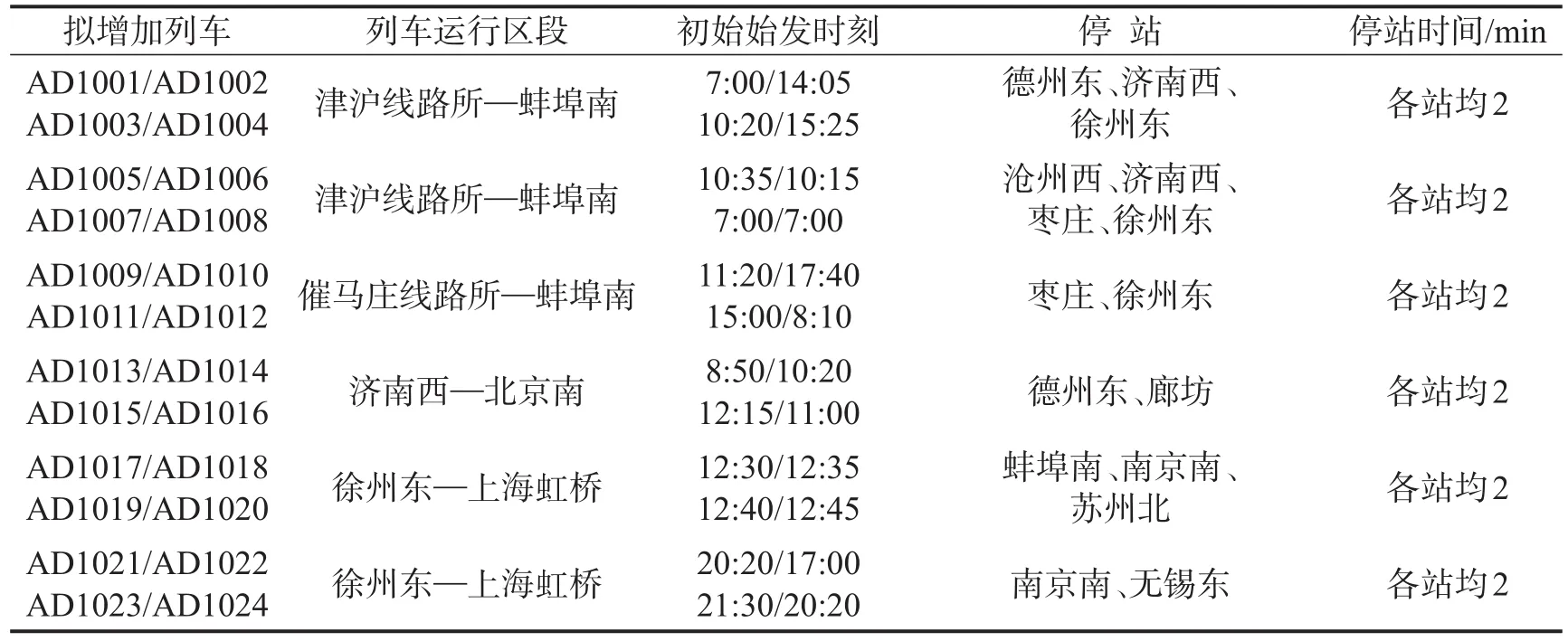
表1 新增列车信息Table 1 New trains’information

本文主要验证模型算法的有效性，求解过程中暂不要求列车上下行数量相等.

首先以现有调整方法进行实验：以初始始发时刻推线求解，结果表明仅能增加AD1015/AD1016、AD1019、AD1023/AD1024次等5条运行线；扩大始发时刻可调整度至60 min，可增加AD1009、 AD1015/AD1016、 AD1018/AD1019、AD1021/AD1022、AD1023/AD1024次等 9条运行线.

然后验证本文所提出模型：给定各运行线初始利润10 000，设αj=10、βj=20、新增列车总停时延长上限为10 min、算法迭代次数上限为200次、运行时间上限为60 min、gap为1%.列车运行参数根据实际情况确定，列车始发时间域以给定的理想始发时刻及可调整度确定.

算例对应规模下，可逐一列出所有簇约束所包含的约束条件.为验证拉格朗日松弛算法效率，调用ILOG CPLEX 12.5求解原模型D进行对比验证.相关算法以C语言实现，实验在1台Ubuntu14.04 Xeon 2.66GHz 4G内存工作站上进行，结果如表2所示，其中C代表CPLEX求解结果，L代表拉格朗日算法求解结果.

可见可增铺运行线数量随列车始发时刻可调整度增加而增加，说明列车始发时间域是影响列车运行图局部调整的重要因素.簇约束式(1)～式(3)使得模型规模急剧增加，CPLEX虽然求解精度较高，但求解速度下降明显；而拉格朗日算法求解时间增加较为平缓，目标函数值、新增列车运行线平均旅速与CPLEX求解所得结果十分接近(表2)，在保证求解质量的同时维持了较高的计算效率.统计不同始发时刻可调整度下拉格朗日算法所得结果如表3所示，其中始发时刻调整总时长、平均时长、最大调整时长分别为相应始发时刻可调整度下各新增运行线较给定理想始发时刻调整值之和、各新增运行线始发时刻调整值均值、各新增运行线最大始发时刻调整度；总停时延长值为相应始发时刻可调整度下各新增运行线较给定最短停时延长值之和.

表2 实验计算结果Table 2 Experiment results

表3 拉格朗日算法计算结果Table 3 Lagrangian algorithm results

实验中随着始发时刻可调整域的增加，相较于根据给定的理想始发时刻推线，由于考虑了列车在站停时可在一定程度上延长，使得运行线求解空间增大，例如在始发时刻可调整度为60 min时，新增运行线在站停时可以在给定最短停时的基础上适当延长(总停时延长不超过10 min)，某站停时的适当延长可能会避免后续铺画时与其他运行线的潜在冲突，在此基础上遍历所有的运行线可行解，增加了新增运行线的铺画概率，因此，相较按理想始发时刻及最短停时推线，额外增铺了6条运行线；但同时由于全程停时的增加，引起了旅速在一定程度上的下降.

进一步验证京沪高铁现有运行图框架下的最大能力，将各运行线始发时刻可调整度放宽至4 h，计算满足天窗限制(0:00-6:00)的可新增运行线数.由于簇约束影响，CPLEX无法在给定时间内得到最优解；拉格朗日算法经过200次迭代、509 s后由于迭代次数达到设定上限终止，共铺画了有效运行线18条，说明在算例框架下京沪高铁通过能力已接近饱和，进一步增开列车需对原有框架做出一定调整.

5 结论

针对给定框架下增铺运行线问题，基于时空网络构建整数规划模型，采用基于拉格朗日松弛的启发式算法求解，实例验证得到结论如下：

(1)采用始发时刻推线方法，算例所述情况下能额外铺画9条运行线，而拉格朗日算法能够铺画15条运行线.

(2)除始发时刻可调整度±10 min情景外，拉格朗日算法的求解速度均优于CPLEX.

(3)随着始发时刻可调整度的增加，模型规模急剧增长，CPLEX所需的求解时间快速增加，而拉格朗日算法计算时间增加较平缓，计算效率优势明显.

(4)始发时刻可调整度由10 min增加至60 min时，由于各运行线可行解范围增加，可增铺的运行线由6条增加至15条.

(5)始发时刻可调整度4 h条件下，CPLEX无法在给定时间内求得最优解，拉格朗日算法在现有框架下最多增铺了18条运行线.

在原列车运行图框架不变条件下，新增运行线铺画受既有运行图框架限制较大，下一步将研究既有列车运行图框架可部分调整条件下所需调整的运行线并给出调整方案.