苏彩虹

(天津大学 机械工程学院 高速空气动力学研究室, 天津 300072)

0 引 言

降低气动噪声是大型飞机研制中必然要面对的一个越来越重要的问题。起飞过程中发动机的射流噪声是主要的噪声源之一。近年来，有些大型飞机的航空发动机外罩的尾缘由原来的平滑形改成了波纹状，如图1所示的波音787的发动机。根据一些理论和实验研究，尾缘处的波纹形设计可以以小的推力损失来达到降低噪声的目的[1-2]。但其降噪机理目前未见有理论上的说明。

改变尾缘形状来降低噪声的想法并不是新生事物。在20世纪90年代中期，工业界就开始在发动机喷口处加入锯齿形尾缘，作为一种降噪措施[3]。普遍认为，锯齿的尖角有利于流向涡的产生，增强混合，减小射流在产生噪声的主要区域内的流速，从而降低噪声。喷流噪声主要包括尾缘下游方向的与大尺度结构有关的低频噪声，及与湍流结构相关的高频噪声。实验观察到，锯齿形尾缘的存在使下游低频噪声降低的同时，会使垂直方向上的高频噪声有所提高[3-4]。这是因为，锯齿引起的流向涡使得湍流在喷嘴处增强。而尾缘形状改变引起的与流动中大尺度相关的低频噪声的抑制机制，目前还缺乏充分的认识和理解。尽管在实验方面已经对锯齿的主要参数如长度、渗透度、锯齿数目等做了很多系统而详细的研究[5-6]。然而，这些参数对噪声影响的机理仍未完全认识清楚[5]。

与发动机喷管尾缘处的锯齿尖角不同的是，发动机外罩的波纹形状更加平滑。在发动机外罩外的尾缘下游，罩外的流动和外涵道的环形射流之间形成了环形剪切层，剪切层的高度不稳定性有利于形成大尺度结构[7-8]，是产生下游低频噪声的主要原因[9-10]。因此，波纹形尾缘降噪的机理很可能是，尾缘形状的变化使得其下游的平均流的稳定性发生了改变，从而抑制了由不稳定性产生的大尺度结构，降低了噪声。但迄今仍缺乏相关的分析。本文将从这一角度来探讨发动机波纹形尾缘对下游低频噪声的抑制机理。

剪切层中的大尺度结构与平均流速度剖面拐点导致的Kelvin-Helmholtz不稳定性有关。大量的实验和理论结果表明，大尺度结构的产生是由于平均流的不稳定性，其主要特征和演化可以由线性稳定性理论很好地预测[11-14]。实验也观察到，无论有无波纹形尾缘，相干结构中的压力脉动场与湍流平均流中演化的线性不稳定波一致[15-17]。本文主要采用线性稳定性理论结合直接数值模拟方法，考察波纹形尾缘对于流场线性不稳定性特征的影响，来探讨对噪声的影响。从稳定性的角度来看，平均流速度剖面拐点导致的无粘不稳定性将起主导作用，湍流的影响是次要的。因此，作为机理探讨的初步，本文将针对层流基本流进行分析。但是，从定性的角度看，与实际问题中的湍流情况是相关的。

1 计算模型和数值方法

发动机尾缘的剪切层是轴对称的。作为探讨机理的初步研究，我们将研究对象简化为图2所示的由无限薄平板分隔开的两层流体在平板下游形成的剪切流。

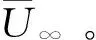
首先考虑平直尾缘的情况。这时基本流是二维的。采用非定常可压缩N-S方程计算基本流。对流项通量分裂后采用5阶迎风格式离散，黏性项采用6阶中心差分格式离散，时间方向采用3步3阶的龙格库塔法，具体公式及方法可参考文献[18]。壁面为无滑移等温壁，温度为284 K。对于平直尾缘的情况，计算域从平板尾缘前0.6 m处开始，不包含平板前缘。入口位置的流场分别由板上下两侧的Blasius相似性解给出。

对于波纹形尾缘的情况，为了避免尾缘形状带来计算上的困难，计算域入口选择在紧靠尾缘的下游处。由于波瓣在流向的尺度不大，在此尺度范围内，沿展向的两层流体的相互作用所产生的影响不会很大，因此在紧靠波瓣的下游处的流速分布，可以由平直尾缘情况下的结果近似地给出。即在展向某处，若该处离尾缘的流向距离为d，则该处的流向速度分布可取为二维问题所得流场在距平板后缘d处的速度分布。而该处的展向速度则取为0。

计算域上下边界、出口边界都采用了缓冲区结合特征边界条件。对于波纹形尾缘情况的计算，展向采用周期性边界条件。需要说明的是，尾缘处为奇点，在计算时，该点的导数由上下两排点的平均值给出。

2 平直尾缘的情况

2.1 基本流场

采用直接数值模拟方法计算基本流场，尾缘位于(0，0)的位置。网格为900×600，不含缓冲区的流向计算域为(-0.3，1.0)，法向计算域为(-0.5，0.5)。流向网格在平板尾缘附近加密，沿下游逐渐放稀。法向网格在上下两侧靠近平板处加密。计算发现，即使不引入人工扰动，在尾缘下游处也会出现非定常的涡结构，如图3所示。这是由于计算差分格式的截断误差相当于一种对流场的扰动，而当网格较密时，计算的格式黏性很小，不足以遏制其影响所导致的。

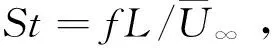
将流向网格数增至1280、2720，可以看到，上述主导模态的性质是一致的。而由于不同网格密度引入的数值扰动的大小有差异，因此流场中主导模态的幅值大小略有差异，如图5所示。在实际问题中，尾缘不可能是无限薄的。在尾缘下游，会出现由于不对称分离而类似于卡门涡街的物理扰动。其频率与尾缘的厚度有关，也与背景扰动的大小有关。

(a) 网格为1280×600

(b) 网格为2720×600

图5不同网格下的傅立叶模态(x=0.53)
(不同颜色的线表示对不同时间段的扰动序列做傅立叶分析)
Fig.5Fouriermodesforcaseswithdifferentmeshes(x=0.53)
(DifferentlinesindicatethattheFourieranalysisisusedforthefluctuationsindifferenttimeperiod)

2.2 流场中的模态分析

根据线性稳定性理论，剪切层中的二维小扰动波可写成如下形式:

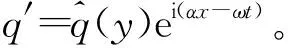
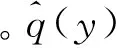
稳定性分析需要得到定常的基本流场。由于流场沿流向的变化缓慢，在流向采用粗网格计算，可以过滤掉小扰动，同时仍得到足够精确而光滑的定常基本流。计算域入口选为平板尾缘处，该处的流场分别由板上下两侧的Blasius相似性解给出。不含缓冲区的流向计算域为(0，2.0)，仅采用90个网格计算，法向计算域和法向网格不变。图6给出了不同流向位置处的速度剖面。从速度剖面的形状不难看出，该流动在x较小时有明显的尾流特征，而往下游则逐步向混合层过渡。由于粗网格不包含尾缘，在尾缘附近得到的流场与2.1节中所得流场必然有所差别。但这个差别在下游会逐渐减小。

对流场进行稳定性分析，发现了两种不稳定的模态，即剪切模态和尾流模态，x=0.06处的特征函数如图7(a)、(b)所示。分别取剪切模态和尾流模态的中性模态的相速度与速度剖面中上、下两个拐点位置处的速度进行比较，如图8所示，发现其分别对应于下、上两个拐点，这说明这两个模态的不稳定性属于无粘拐点不稳定性。这表明，只要平均流速度剖面相同，即使一个是层流，一个是湍流，其稳定性特征也相近。

为了进一步说明粗网格下流场稳定性是可信的，我们将网格密度为2720×600下得到的流场和本节粗网格得到的最不稳定剪切模态的频率(为了与2.1节对应，已从圆频率转化为频率)和增长率进行比较，结果如图9(a)、(b)所示。密网格只计算至x=0.25，因为再往下游会出现明显的不定常涡。从趋势上来看，两者符合很好。因此，采用粗网格得到的流场进行稳定性分析，可以反映真实的情况。

(a) 剪切模态

(b) 尾流模态

图7剪切模态和尾流模态的特征函数
Fig.7Eigenfunctionofshearlayermodeandwakemode

(a) 频率

(b) 增长率

图9粗细网格下最不稳定的剪切模态的比较
Fig.9Comparisonofthemostamplifiedshearlayermodeobtainedfromfineandcoarsemeshes

为了说明2.1节发现的主导模态，我们给出了不同流向位置处两种模态最不稳定波的频率和增长率，如图10所示。可见，在x=0.06处，最不稳定的尾流模态和剪切模态的频率分别为6.67和23.4，这与2.1节图4(b)中直接数值模拟给出的主导模态刚好吻合。而从图10(b)给出的增长率上可以看出，剪切模态更不稳定，因此，它能更快增长，成为流场中的主导模态。将图4给出的不同流向位置处剪切模态的幅值记录下来，与线性稳定性理论得到的幅值进行比较。由于初始扰动幅值未知，比较时令x=0.2处线性理论(LST)与直接数值模拟结果(DNS)相等。结果如图11所示。可见，线性理论在一定范围内仍然适用。这也说明，2.1节图3中出现的涡对应的是流场中最不稳定的剪切模态。

(a) 频率

(b) 增长率

图10不同流向位置的最不稳定扰动
Fig.10Themostamplifiedmodeatdifferentstreamwiselocations

2.3 板下侧为马赫数0.5的情况

取板下侧马赫数为0.5，用2.2节的粗网格计算基本流场，不同流向位置处的流向速度剖面如图12所示。与图6给出的板下侧马赫数为0.35的结果相比，由于两侧速度比增大，混合层的特征更加显著。对该剖面进行线性稳定性分析，仍可以找到剪切模态和尾流模态。图13(a)、(b)分别给出了最不稳定的剪切模态和尾流模态的频率、增长率与板下侧马赫数为0.35的结果的比较(M2表示板下侧马赫数)。可见，下侧流动马赫数从0.35增大至0.5，两种模态的最不稳定波的频率相近，剪切模态的增长率增大，尾流模态的增长率减小。这与平均流剖面中混合层的两侧速度比增大有关。

针对马赫数为0.5的情况，也采用2.1节所示的密网格计算了尾缘后涡的情况，并采用傅里叶方法得到了起主导作用的模态。结果发现，与马赫数0.35的情况在定性上是完全一致的。因此，不再赘述。对于尾缘为波纹形的情况，我们只针对马赫数为0.35的情况进行了计算。

3 波纹形尾缘的情况

取余弦函数作为尾缘的形状，如图14所示。尾缘有波纹形时展向计算域为(-0.075，0.075)，每个波纹的宽度为zl=0.15，深度为h=0.1。将计算域入口取在x=0.1处。该处的速度场根据平直尾缘的基本流场插值近似地给出。计算方法与第2节相同，仍采用粗网格流场进行计算，得到稳定的基本流场。图15给出了计算得到的在z=0处，不同流向位置处的速度剖面。为了便于比较，将平直尾缘情况下的尾缘移至x=0.05处。

在波纹形尾缘的情况下，不存在二维扰动。采用全局不稳定性进行稳定性分析，可以得到不同流向位置处的特征函数，如图16所示。这里只考虑放大率较大的剪切模态。假设在x=0.15处，平直尾缘和波纹形尾缘两种情况下扰动的初始幅值均为1，可找到x=0.15～0.5范围内幅值放大最大的扰动，其频率均在23左右(转化为有量纲的频率为1.3kHz左右)，其放大倍数的比较如图17所示。可见，尾缘的波纹形使最危险的扰动放大倍数显著减小。

根据Lighthill声比拟理论，雷诺应力的二阶导数项为气动噪声源。图18给出了根据线性理论计算得到的x=0.3处雷诺应力二阶导数中最大的一项的比较(x=0.15处扰动脉动幅值设为1)。对于波纹形尾缘的情况，不同的线对应于不同的展向位置。可见，雷诺应力二阶导数也显著减小。

类似地，采用相同的密网格对波纹形尾缘的情况进行直接数值模拟计算，流场中可见非定常涡的出现。以x=0.22为例，分别在z=0(波纹顶点处)、z=-0.075(波纹根部)记录扰动的时间序列进行傅立叶分析，并与平直尾缘的情况进行比较，结果如图19所示。可见，尾缘为波纹形时主导频率的幅值显著降低。与平直尾缘的情况相比，降低了一个量级。

4 结 论

本文采用直接数值模拟方法结合线性稳定性理论分析，探讨了发动机波纹形尾缘降噪的机理。对于平直尾缘的情况，研究发现，尾缘后存在的非定常涡，对应的正是平均流中最不稳定的二维剪切模态。而对于波纹形尾缘的情况，则不存在二维模态。对三维平均流的全局稳定性分析显示，所得三维最不稳定模态的增长率显著低于平直尾缘的情况，幅值放大倍数显著小于二维的情况，并且，作为声源项的雷诺应力的二阶导数项也显著减小。

因此，对于发动机尾缘采用波纹形的降噪机理，可以归结为，波纹的存在改变了平均流的稳定性特性，从而抑制了最不稳定模态的增长，使得声源项中雷诺应力的二阶导数项也相应大幅减小，从而降低了噪声。

致谢:感谢天津大学周恒教授在此工作中给予作者的启发性的建议和帮助。感谢天津大学赵磊博士提供全局稳定性分析程序。此项工作在国家超算天津中心“天河一号”完成,特此致谢。

参 考 文 献：

[1]Xia H, Tucker P G, Eastwood S. Large-eddy simulations of chevron jet flows with noise predictions[J]. International Journal of Heat and Fluid Flow, 2009, 30(6): 1067-1079.

[2]Howe M. Aerodynamic noise of a serrated trailing edge[J]. Journal of Fluids and Structures, 1991, 5(1): 33-45.

[3]Zaman K B M Q, Bridges J E, Huff D L. Evolution from ‘tabs’ to ‘chevron technology’-a review[J]. Noise Notes, 2012, 11(1): 27-48.

[4]Pauz V, Niemoeller A, Meinke M H, et al. Numerical analysis of chevron nozzle noise[C]//23rd AIAA/CEAS Aeroacoustics Conference. 2017: 3853.

[5]Koch L D, Bridges J, Khavaran A. Mean flow and noise prediction for a separate flow jet with chevron mixers[C]//Proc 42nd AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, USA. AIAA 2004-0189.

[6]Bridges J, Brown C A. Parametric testing of chevrons on single flow hot jets[C]//Proc 10th AIAA/CEAS Aeroacoustics Conference. Manchester, Great Britain. AIAA 2004-2824.

[7]Brown G L, Roshko A. On density effects and large structure in turbulent mixing layers[J]. Journal of Fluid Mechanics, 1974, 64(4): 775-816.

[8]Clemens N T, Mungal M G. Large-scale structure and entrainment in the supersonic mixing layer[J]. Journal of Fluid Mechanics, 1995, 284: 171-216.

[9]Crawley M, Sinha A, Samimy M. Near-field and acoustic far-field response of a high-speed jet to excitation[J]. AIAA Journal, 2015, 53(7): 1-16.

[10]Araki M, Morita K, Takahashi Y, et al. Experimental investigation of jet noise sources in a hypersonic nozzle at takeoff[J]. AIAA Journal, 2015, 53(3): 789-794.

[11]Gaster M, Kit E, Wygnanski I. Large-scale structures in a forced turbulent mixing layer[J]. Journal of Fluid Mechanics, 1985, 150(150): 23-39.

[12]Liu J T C. Coherent structures in transitional and turbulent free shear flows[J]. Annual Review of Fluid Mechanics, 1989, 21(1): 285-315.

[13]Wu X, Zhuang X. Nonlinear dynamics of large-scale coherent structures in turbulent free shear layers[J]. Journal of Fluid Mechanics, 2016, 787: 396-439.

[14]Ran L, Ye C, Wan Z, et al. Instability waves and low-frequency noise radiation in the subsonic chevron jet[J]. Acta Mechanica Sinica, 2018, 34(3): 421-430.

[15]Suzuki T, Colonius T. Instability waves in a subsonic round jet detected using a near-field phased microphone array[J]. Journal of Fluid Mechanics, 2006, 565(565): 197-226.

[16]Sinha A, Gudmundsson K, Xia H, et al. Parabolized stability analysis of jets from serrated nozzles[J]. Journal of Fluid Mechanics, 2016, 789: 36-63.

[17]Gudmundsson K, Colonius T. Spatial stability analysis of chevron jet profiles[R]. AIAA 2007-3599.

[18]Su C H. Physical implication of two problems in transition prediction of boundary layers based on linear stability theory[J]. Sci China Phys Mech Astron, 2014, 57(5):950-962.