孙 荣

（重庆工商大学 数学与统计学院，重庆 400067）

0 引言

对于风险定价,信度理论是一种重要的经验定价方法。信度理论产生于20世纪20年代，至今已有90多年的历史，在非寿险精算理论与实务中具有重要地位，精算师根据过去的单个风险或者一个保单组合风险的经验数据，调整未来的保险费。信度理论的研究主要形成了两个不同的分支：（1）建立在频率方法上的有限扰动理论；（2）以贝叶斯理论为基础的最精确一可信度理论。这两种方法都是希望通过已有的历史数据来合理地制定保费。

在已有的风险理论中,个体风险常常假设是相互独立的,主要是因为独立假定比具有一定相关性的假定在数学的处理上更容易一些。Li（2000）[1],Cheng（2003）等[2]研究了保险风险独立同分布的情况下保费与风险载荷非参数估计量的弱、强收敛性与渐进正态性，但在保险实践中，在很多情况下，个体风险由于它们有相同的索赔产生机制或是由于共同的经济和物理环境的影响，表现出一定的相关性，因此，对相依结构下保险风险的非参数估计研究具有更为重要的理论价值和现实意义。本文在保险风险具有强混合特点的相依结构前提下，提出了基于PH变换与条件尾期望原理的保费与风险载荷的非参数估计量，分析了相关估计量的强收敛性与渐近正态性。除了少数异常值情况外，蒙特卡洛的实证证据显示了它们良好的估计精度。

1 主要结论与定理

在精算科学中，保险风险X常常界定为一个非负的随机变量，其相对应的保费是保险风险的一个函数：H(X):X→[0 ' ∞ )。假设F为保险风险X的分布函数，定义S=1-F.Wang[3-5]将PH-变换保费定义为：

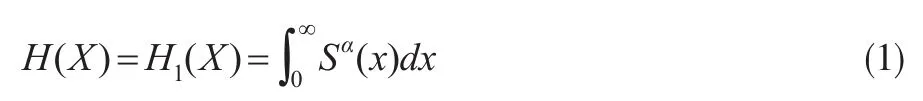
其中α∈(0 ' 1)是一个常数。假设保险风险X的期望 E(X)存在，另一个重要的指标是风险载荷D(X)=H(X)-E(X),因此将PH-变换下的风险载荷定义为：

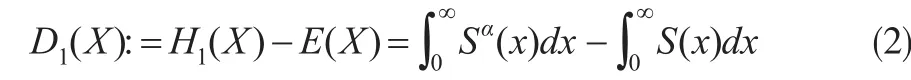
条件尾期望原理下的保费定义为：

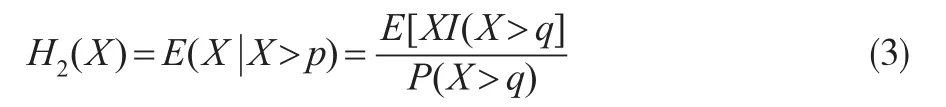
由于保险风险常常是相互关联的，所以本文提出一种相依结构来分析这种相依关系。假设 {ξi'i=1'2'…}是概率空间{Ω 'F'P}上的实值随机变量序列，表示由(ξ'm≤i≤n)生成的σ-域：

i

当n→∞时，α(n)→0，则随机变量序列{ξi'i=1'2'…}称为 α-混合或者强混合。强混合序列的概念最先是由Rosenblat（t1956）提出的，现在被广泛用于时间序列及随机领域的极限理论分析。α-混合结构的条件要弱于其他混合，如m-相依、φ-混合、ρ-混合、绝对正则等，同时很多滑动平均混合序列和线性时间序列都是α-混合的。所以α-混合能比较合理地刻画时间序列模型的相依结构，有着广泛的应用领域[6]。

在概率空间{Ω 'F'P}上定义保险风险的经验分布函数为：

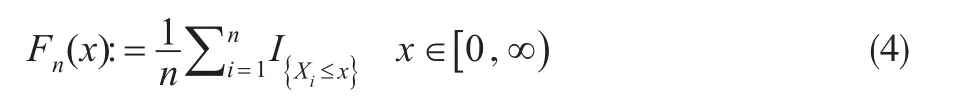
因此从式(1)至式(4)可以得到PH-变换保费H1(X)及风险载荷D1(X)的估计量分别为：

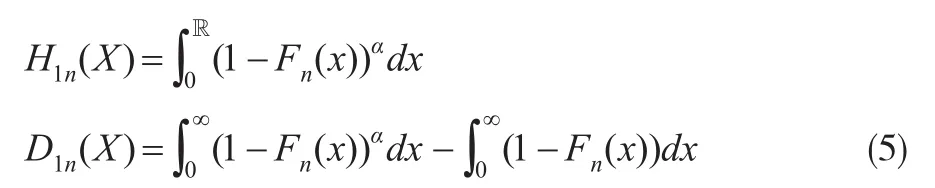
以及条件尾期望原理下的保费 H2(X)与风险载荷D2(X)的估计量分别为：

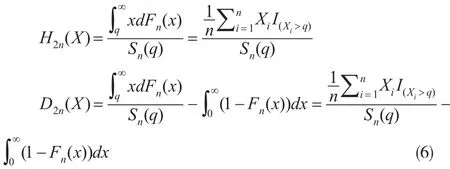
其中:Sn(q)=1-Fn(q)。

定理1：假设保险风险{Xi'i=1'…n}是一严平稳的α- 混合序列,α(n)=o(ρn)，0＜ρ＜1，如果存在 δ＞0使得EX1+δ＜∞ ，则：

定理2：假设保险风险{Xi'i=1'…n}是一严平稳的α-混合序列,如果存在1＜r≤2使得 E | X|r＜∞ 。存在θ＞(s-1)r/(r-s)使得α(n)≤Cn-θ，其中1＜s＜r，则：

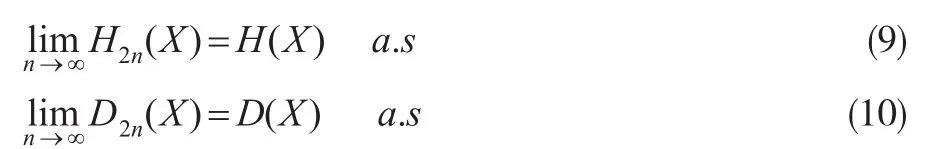
定理3：假设保险风险{Xi'i=1'…n}是一严平稳的α- 混合序列,令 ζi=XiI(X＞q)-EXI(X＞q),如果＞0,且存

i在 δ＞0 使得 E | X|2+δ＜∞,当(k)＜∞ ，其中 δ＞0,则：

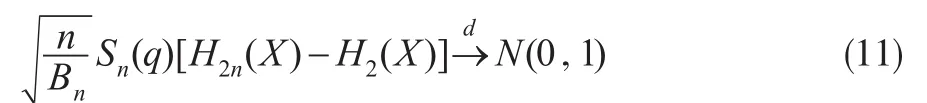
令 ψi=Xi[I(X＞q)-S(q)]-[EXI(X＞q)-S(q)EX],如果 Eψ12

i＞0,则：

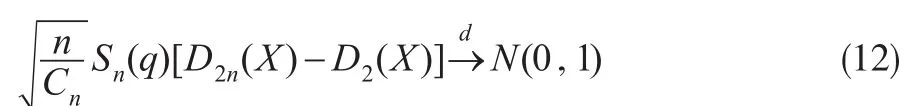
其中

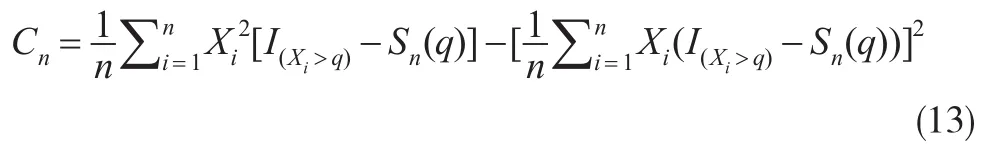
引理 1[6]：{Xi'i≥1}为 R中的平稳 α-混合序列，α(n)=o(ρn)，0＜ρ＜1，M 为大于1的正整数，则存在仅依赖于混合系数的常数C1，C2，对∀0＜θ＜1，ε＞0，存在正整数r*＞0，当正整数r＞r*时，有：

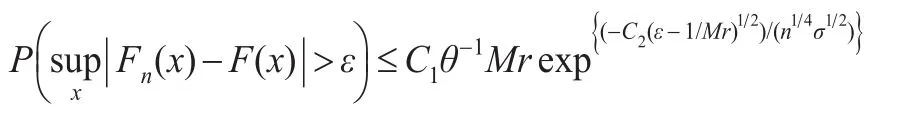
定理1的证明：

对∀ω及T＞0,

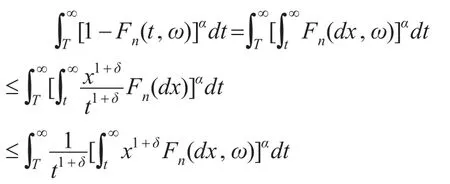
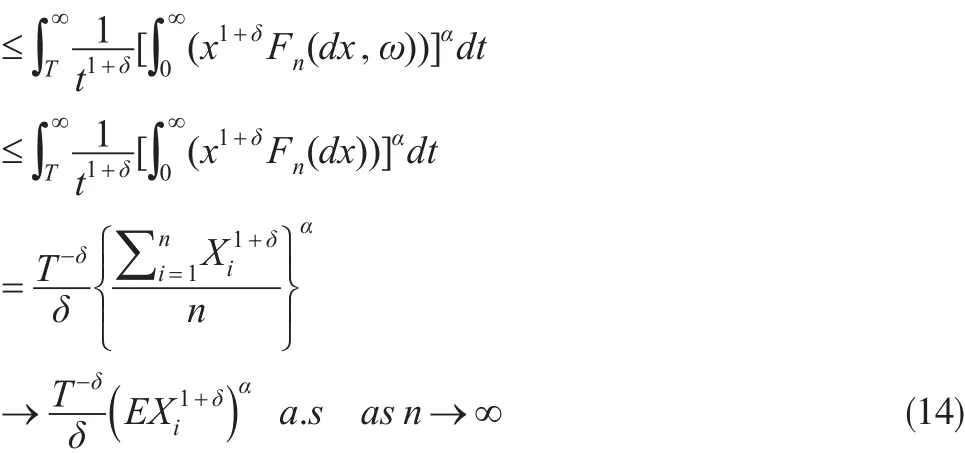
最后一个收敛结果来自于文献[7]中的定理2.1。

因为 EX1+δ＜∞,所以：

由于：

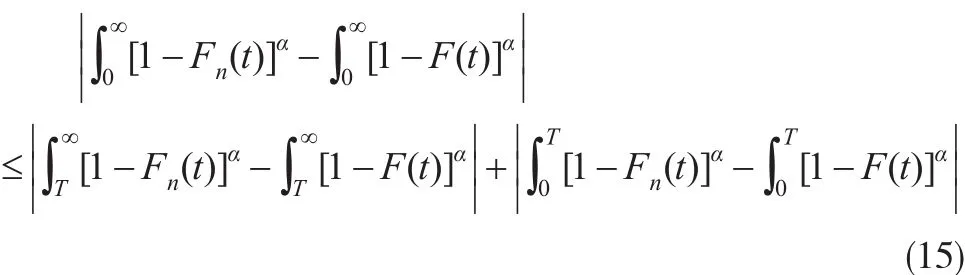
由引理1利用Borel-Cantelli定理可得：

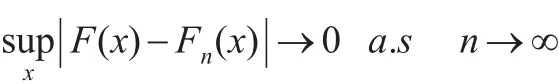
并利用α-混合序列的Bernstein矩不等式[8]，分别令n→∞，T→∞,由控制收敛定理及式(5)、式(10)、式(11),可以得到式(7)。合并上面的结果及引理1同样可以得到式(8)。

定理2的证明：

从文献[7]中的定理2.2,可以得到:由式(6)、式(16)、式(17)可得到式(9),由式(6)、式(9)、式(16)、式(17)及文献[7]中的定理2.2可得到式(10)。

定理3的证明：

令

从式(13)容易得到:

由定理中假定的严平稳性及 EX2+δ＜∞可以得到:

运用文献[9,10]中类似方法，采用bernstein big-block与small-block程序，选择 p=pn,q=qn,k=kn。令:

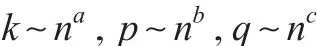
其中 a+b＜1,a+c＜1,a'b'c＞0,这些条件可以保证式(21)：

记：

则:

由定理已知条件及式(18)至式(23)可得:

因此，由式(24)可知式(23)右端的两项是渐进可忽略的。

由严平稳性及文献[11]中的引理1。

设 ρk=E(ζ0ζk)

可得:

则Lindberg条件是满足的,Lyaponov’s定理成立。

式(11)得证，同理可类似证得式(12)。

2 统计模拟

首先，为了保证保险风险的非负性,从均匀分布U[0'1]中产生相互独立的n+1个数据然后为了满足本文所设定的相依结构，令:yi=rx1+x1+i,i=1'…,n。

其中:分别设定r=0.6'r=0.3'r=0.1'n=100,200,300,α=1/2,q=0.2,名义的置信度为0.90,0.95,0.99.通过1000次重复模拟,计算相关指标。

为了评价相关估计量的估计质量，本文选择了两个指标进行评价，一个是估计的均方误差，另一个是置信区间覆盖概率。

从H1n(X)和H2n(X)这两个估计量的MSE来看:由表1，在 r=0.1'r=0.3'r=0.6'随着r值的增加,两者的均方误差总体呈现一种向上的变化趋势,同时随着样本容量的增加,均方误差有改善,说明相依程度与样本容量与MSE有关联。当n＞200,r=0.1'r=0.3'H1n(X)的MSE略低于H2n(X),当 n＜200,看不出两者的差别性。

表1 MSE forH(X)

总体来说，这两个估计量都显示了当r较小，样本容量n相对较大时，估计精度优于 r较大n较小时。

从 H2n(X)的置信区间覆盖概率来看：由表2,在r=0.1'r=0.3'r=0.6'随着r值的增加，计算的样本置信区间覆盖概率，总体上呈现一种与名义置信度偏离程度越大的趋势。同时，随着样本的增加，偏离程度有所减小。说明相依程度与样本容量与置信区间覆盖概率也具有一定关联性。总体来看，本文所提出的估计量H2n(X)估计性能是优良的。置信区间覆盖概率与名义置信度偏离程度的变化范围在10%左右，特别在r=0.1，样本容量n=300时，n=300，覆盖概率是非常接近于名义置信度的。从不同的名义置信度来看，模拟结果并没有显示出优劣性不同水平的覆盖概率的优劣性。

表2 Coverage probabilities forH2(X)

从上可以看出，本文所提出的相关估计量可以运用于对保险风险相关指标的估计，特别是在相关程度低，样本容量较大的条件下具有更高的拟合优度。

3 结论

在保险风险相依结构，即保险风险序列是严平稳的α-混合序列的条件下，本文提出了在不同保费原理下对保费与相应风险载荷的非参数估计方法，从理论上分析了相关估计量的强收敛性与渐进正态性。在统计模拟过程中采用两个指标评价估计量的性能：一个是估计的均方误差，另一个是置信区间覆盖概率，从模拟结果来看，相关估计量表现出了优良的估计性质。可以作为保险实践中的保费与风险载荷的估计量。

[1]Li D Y.On Right Tail Index[D].Beijing：Peking University Press,2000.

[2]Cheng S H,Wang X Q and Yang J P.On a Kind of Integrals of Empirical Processes Concerning Insurance Risk[J].Chinese Science:Mathematics(English Edition),2003,46(2).

[3]Wang S.An Actuarial Index of the Right Tail Risk[J].North American Actuarial Journal,1997,(2).

[4]Wang S.Insurance Pricing and Increased Limits Rate Making by Proportional Hazards Transforms[J].IME,1995，(17).

[5]Wang S,Young V R,Panjer H H.Axiomatic Characterization of Insurance Prices[J].IME1997，(21).

[6]孙荣.基于随机窗宽的α-混合序列分布函数估计[J].统计与决策,2016,（11）.

[7]Xing G D,Yang S C,Chen A W.A Maximal Moment Inequality for Mixing Sequences and Applications[J].Statist.Probab.Lett,2009,79(12).

[8]Chaigenxiang.Consistent Estimation of Randon Window-width Kernel of Distribution Function[J].Scientiasinica(Series A),1984,11(1).

[9]Li yongming,Yao jing,Ying rui.A Central Limit Theorem for strong Mixing Sequence and its Applicationin Regression Model[J].Mathmat-ica applicata,2016,29(1).

[10]Li Y M Li J.A Note on the Central Limit Theorem for Strong Mixing Sequences[J].Chinese J.Applied Probab.Statist.,2013,29(1).

[11]Yang S C.Bounds for Strong Mixing Sequences and Their Application[J].J.Mathematical Rasearch and Exposition,2000,20(3).